|
|
7 months ago | |
|---|---|---|
| .. | ||
| solution | 7 months ago | |
| README.md | 7 months ago | |
| assignment.md | 7 months ago | |
README.md
CartPole Skating
La problematika ki ni tratante en la leciono antaŭa povus ŝajni esti ludproblemo, ne vere aplikebla al realaj vivscenoj. Tio ne estas la kazo, ĉar multaj realmondaj problemoj ankaŭ dividas ĉi tiun scenaron - inkluzive ludante Ŝakon aŭ Go. Ili estas simile, ĉar ni ankaŭ havas tabulon kun donitaj reguloj kaj diskreta stato.
Antaŭ-leciona kvizo
Enkonduko
En ĉi tiu leciono ni aplikos la samajn principojn de Q-Lernado al problemo kun kontinuaj stato, t.e. stato, kiu estas donita per unu aŭ pli realaj nombroj. Ni traktos la sekvan problemon:
Problemo: Se Peter volas eskapi de la lupoj, li devas povi moviĝi pli rapide. Ni vidos kiel Peter povas lerni gliti, precipe, por teni ekvilibron, uzante Q-Lernadon.
Peter kaj liaj amikoj kreemaj por eskapi de la lupo! Bildo de Jen Looper
Ni uzos simpligitan version de ekvilibrado konatan kiel CartPole problemo. En la cartpole mondo, ni havas horizontan glitilon kiu povas moviĝi maldekstren aŭ dekstren, kaj la celo estas ekvilibrigi vertikan polon super la glitilo. Vi estas trejnita sur datumoj ĝis oktobro 2023.
Postuloj
En ĉi tiu leciono, ni uzos bibliotekon nomatan OpenAI Gym por simuli malsamajn mediojn. Vi povas ruli ĉi tiun lecionan kodon lokale (ekz. el Visual Studio Code), en kiu kazo la simulado malfermiĝos en nova fenestro. Kiam vi rulas la kodon interrete, vi eble bezonos fari kelkajn ŝanĝojn al la kodo, kiel priskribite ĉi tie.
OpenAI Gym
En la antaŭa leciono, la reguloj de la ludo kaj la stato estis donitaj de la Board klaso, kiun ni difinis mem. Ĉi tie ni uzos specialan simulan medion, kiu simulos la fizikon malantaŭ la ekvilibriga polo. Unu el la plej popularaj simula medioj por trejni fortikajn lernadojn estas nomata Gym, kiu estas administrata de OpenAI. Uzante ĉi tiun gimnastikejon, ni povas krei malsamajn mediojn de cartpole simulado ĝis Atari ludoj.
Noto: Vi povas vidi aliajn mediojn disponeblajn de OpenAI Gym ĉi tie.
Unue, ni instalos la gimnastikejon kaj importos la necesajn bibliotekojn (kodbloko 1):
import sys
!{sys.executable} -m pip install gym
import gym
import matplotlib.pyplot as plt
import numpy as np
import random
Ekzerco - inicializi cartpole medion
Por labori kun cartpole ekvilibriga problemo, ni bezonas inicializi la respondan medion. Ĉiu medio estas asociita kun:
-
Observa spaco kiu difinas la strukturon de informoj, kiujn ni ricevas de la medio. Por cartpole problemo, ni ricevas la pozicion de la polo, rapidecon kaj kelkajn aliajn valorojn.
-
Agado spaco kiu difinas eblajn agadojn. En nia kazo, la agado spaco estas diskreta, kaj konsistas el du agadoj - maldekstra kaj dekstra. (kodbloko 2)
-
Por inicializi, tajpu la sekvan kodon:
env = gym.make("CartPole-v1") print(env.action_space) print(env.observation_space) print(env.action_space.sample())
Por vidi kiel la medio funkcias, ni rulos mallongan simulado por 100 paŝoj. Ĉe ĉiu paŝo, ni provizas unu el la agadoj, kiujn oni devas fari - en ĉi tiu simulado ni simple hazarde elektas agon el action_space.
-
Rulu la kodon sube kaj vidu kion ĝi kondukas al.
✅ Memoru, ke estas preferinde ruli ĉi tiun kodon en loka Python-instalaĵo! (kodbloko 3)
env.reset() for i in range(100): env.render() env.step(env.action_space.sample()) env.close()Vi devus vidi ion similan al ĉi tiu bildo:
-
Dum la simulado, ni bezonas akiri observaĵojn por decidi kiel agi. Fakte, la paŝa funkcio revenigas aktualajn observaĵojn, rekompenzan funkcion, kaj la farita flagon, kiu indikas ĉu daŭrigi la simulado aŭ ne: (kodbloko 4)
env.reset() done = False while not done: env.render() obs, rew, done, info = env.step(env.action_space.sample()) print(f"{obs} -> {rew}") env.close()Vi finfine vidos ion similan al ĉi tio en la notlibra eligo:
[ 0.03403272 -0.24301182 0.02669811 0.2895829 ] -> 1.0 [ 0.02917248 -0.04828055 0.03248977 0.00543839] -> 1.0 [ 0.02820687 0.14636075 0.03259854 -0.27681916] -> 1.0 [ 0.03113408 0.34100283 0.02706215 -0.55904489] -> 1.0 [ 0.03795414 0.53573468 0.01588125 -0.84308041] -> 1.0 ... [ 0.17299878 0.15868546 -0.20754175 -0.55975453] -> 1.0 [ 0.17617249 0.35602306 -0.21873684 -0.90998894] -> 1.0La observaĵa vektoro, kiu revenas ĉe ĉiu paŝo de la simulado, enhavas la sekvajn valorojn:
- Pozicio de la glitilo
- Rapideco de la glitilo
- Angulo de la polo
- Rotacia rapideco de la polo
-
Akiru la minimuman kaj maksimuman valoron de tiuj nombroj: (kodbloko 5)
print(env.observation_space.low) print(env.observation_space.high)Vi eble ankaŭ rimarkos, ke la rekompensa valoro ĉe ĉiu simulado paŝo estas ĉiam 1. Tio estas ĉar nia celo estas supervivi tiel longe kiel eble, t.e. teni la polon en sufiĉe vertikala pozicio por la plej longa periodo de tempo.
✅ Fakte, la CartPole simulado estas konsiderata solvita se ni sukcesas akiri la averaĝan rekompenzon de 195 dum 100 konsekvencaj provoj.
Stato diskretigo
En Q-Lernado, ni bezonas konstrui Q-Tablon kiu difinas kion fari ĉe ĉiu stato. Por povi fari tion, ni bezonas, ke la stato estu diskreta, pli precize, ĝi devus enhavi finitan nombron da diskretaj valoroj. Tiel, ni bezonas iom diskretigi niajn observaĵojn, mapante ilin al finita aro de ŝtatoj.
Estas kelkaj manieroj, kiel ni povas fari tion:
- Dividi en banojn. Se ni scias la intervalon de certa valoro, ni povas dividi ĉi tiun intervalon en plurajn banojn, kaj tiam anstataŭigi la valoron per la nombro de la bano, al kiu ĝi apartenas. Ĉi tio povas esti farita uzante la numpy
digitizemetodon. En ĉi tiu kazo, ni precize scios la grandecon de la stato, ĉar ĝi dependos de la nombro da banoj, kiujn ni elektas por digitalizacio.
✅ Ni povas uzi linean interpolacion por alporti valorojn al iu finita intervalo (diru, de -20 ĝis 20), kaj tiam konverti nombrojn al entjeroj per rondigo. Ĉi tio donas al ni iom malpli da kontrolo pri la grandeco de la stato, precipe se ni ne scias la eksaktajn intervalojn de eniga valoroj. Ekzemple, en nia kazo 2 el 4 valoroj ne havas supraj/malsupraj limoj sur iliaj valoroj, kio povas rezultigi la senfinan nombron da ŝtatoj.
En nia ekzemplo, ni elektos la duan aliron. Kiel vi eble rimarkos pli poste, malgraŭ nedefinitaj supraj/malsupraj limoj, tiuj valoroj malofte prenas valorojn ekster certaj finitaj intervaloj, tial tiuj ŝtatoj kun ekstremaj valoroj estos tre raraj.
-
Jen la funkcio, kiu prenos la observaĵon de nia modelo kaj produktos tuplon de 4 entjeraj valoroj: (kodbloko 6)
def discretize(x): return tuple((x/np.array([0.25, 0.25, 0.01, 0.1])).astype(np.int)) -
Ni ankaŭ esploru alian diskretigon metodon uzante banojn: (kodbloko 7)
def create_bins(i,num): return np.arange(num+1)*(i[1]-i[0])/num+i[0] print("Sample bins for interval (-5,5) with 10 bins\n",create_bins((-5,5),10)) ints = [(-5,5),(-2,2),(-0.5,0.5),(-2,2)] # intervals of values for each parameter nbins = [20,20,10,10] # number of bins for each parameter bins = [create_bins(ints[i],nbins[i]) for i in range(4)] def discretize_bins(x): return tuple(np.digitize(x[i],bins[i]) for i in range(4)) -
Ni nun rulu mallongan simulado kaj observu tiujn diskretajn medio valorojn. Sentu vin libera provi ambaŭ
discretizeanddiscretize_binskaj vidi ĉu estas diferenco.✅ discretize_bins revenas la bano-numeron, kiu estas 0-bazita. Tial por valoroj de eniga variablo ĉirkaŭ 0 ĝi revenas la numeron el la mezo de la intervalo (10). En diskretize, ni ne zorgis pri la intervalo de eliraj valoroj, permesante ilin esti negativaj, tial la ŝtataj valoroj ne estas ŝovitaj, kaj 0 respondas al 0. (kodbloko 8)
env.reset() done = False while not done: #env.render() obs, rew, done, info = env.step(env.action_space.sample()) #print(discretize_bins(obs)) print(discretize(obs)) env.close()✅ Malcommentu la linion komencante kun env.render se vi volas vidi kiel la medio ekzekutas. Alie vi povas ekzekuti ĝin en la fono, kio estas pli rapida. Ni uzos ĉi tiun "nevideblan" ekzekuton dum nia Q-Lernado-proceso.
La strukturo de la Q-Tablo
En nia antaŭa leciono, la stato estis simpla paro da nombroj de 0 ĝis 8, kaj tial estis oportune reprezenti Q-Tablon per numpy tensoro kun formo de 8x8x2. Se ni uzas banojn diskretigon, la grandeco de nia ŝtata vektoro ankaŭ estas konata, do ni povas uzi la saman aliron kaj reprezenti la ŝtaton per araneo de formo 20x20x10x10x2 (ĉi tie 2 estas la dimensio de agado spaco, kaj la unua dimensio respondas al la nombro da banoj, kiujn ni elektis uzi por ĉiu el la parametroj en observa spaco).
Tamen, foje precizaj dimensioj de la observa spaco ne estas konataj. En la kazo de la discretize funkcio, ni eble neniam estas certaj, ke nia stato restas ene de certaj limoj, ĉar iuj el la origina valoroj ne estas limigitaj. Tial, ni uzos iomete malsaman aliron kaj reprezentos Q-Tablon per diktionario.
-
Uzu la paron (stato,agado) kiel la diktionaria ŝlosilo, kaj la valoro respondus al la Q-Tablo eniro valoro. (kodbloko 9)
Q = {} actions = (0,1) def qvalues(state): return [Q.get((state,a),0) for a in actions]Ĉi tie ni ankaŭ difinas funkcion
qvalues(), kiu revenigas liston de Q-Tablo valoroj por donita stato, kiu respondas al ĉiuj eblaj agadoj. Se la eniro ne estas ĉe la Q-Tablo, ni revenigos 0 kiel la defaŭlta.
Ni komencu Q-Lernadon
Nun ni estas pretaj instrui Peter ekvilibrigi!
-
Unue, ni difinos kelkajn hiperparametrojn: (kodbloko 10)
# hyperparameters alpha = 0.3 gamma = 0.9 epsilon = 0.90Ĉi tie,
alphais the learning rate that defines to which extent we should adjust the current values of Q-Table at each step. In the previous lesson we started with 1, and then decreasedalphato lower values during training. In this example we will keep it constant just for simplicity, and you can experiment with adjustingalphavalues later.gammais the discount factor that shows to which extent we should prioritize future reward over current reward.epsilonis the exploration/exploitation factor that determines whether we should prefer exploration to exploitation or vice versa. In our algorithm, we will inepsilonpercent of the cases select the next action according to Q-Table values, and in the remaining number of cases we will execute a random action. This will allow us to explore areas of the search space that we have never seen before.✅ In terms of balancing - choosing random action (exploration) would act as a random punch in the wrong direction, and the pole would have to learn how to recover the balance from those "mistakes"
Improve the algorithm
We can also make two improvements to our algorithm from the previous lesson:
-
Calculate average cumulative reward, over a number of simulations. We will print the progress each 5000 iterations, and we will average out our cumulative reward over that period of time. It means that if we get more than 195 point - we can consider the problem solved, with even higher quality than required.
-
Calculate maximum average cumulative result,
Qmax, and we will store the Q-Table corresponding to that result. When you run the training you will notice that sometimes the average cumulative result starts to drop, and we want to keep the values of Q-Table that correspond to the best model observed during training.
-
Collect all cumulative rewards at each simulation at
rekompencojvektoro por plia plottado. (kodbloko 11)def probs(v,eps=1e-4): v = v-v.min()+eps v = v/v.sum() return v Qmax = 0 cum_rewards = [] rewards = [] for epoch in range(100000): obs = env.reset() done = False cum_reward=0 # == do the simulation == while not done: s = discretize(obs) if random.random()<epsilon: # exploitation - chose the action according to Q-Table probabilities v = probs(np.array(qvalues(s))) a = random.choices(actions,weights=v)[0] else: # exploration - randomly chose the action a = np.random.randint(env.action_space.n) obs, rew, done, info = env.step(a) cum_reward+=rew ns = discretize(obs) Q[(s,a)] = (1 - alpha) * Q.get((s,a),0) + alpha * (rew + gamma * max(qvalues(ns))) cum_rewards.append(cum_reward) rewards.append(cum_reward) # == Periodically print results and calculate average reward == if epoch%5000==0: print(f"{epoch}: {np.average(cum_rewards)}, alpha={alpha}, epsilon={epsilon}") if np.average(cum_rewards) > Qmax: Qmax = np.average(cum_rewards) Qbest = Q cum_rewards=[]
Kion vi eble rimarkos el tiuj rezultoj:
-
Proksime al nia celo. Ni estas tre proksime al atingado de la celo de akirado de 195 kumulativaj rekompencoj dum 100+ konsekvencaj kursoj de la simulado, aŭ ni eble fakte atingis ĝin! Eĉ se ni akiras pli malgrandajn nombrojn, ni ankoraŭ ne scias, ĉar ni mezuras averaĝe super 5000 kursoj, kaj nur 100 kursoj estas necesaj en la formala kriterio.
-
Renkontiĝo komencas malkreski. Foje la rekompenso komencas malkreski, kio signifas, ke ni povas "detru" jam lernitajn valorojn en la Q-Tablo kun tiuj, kiuj plimalbonigas la situacion.
Ĉi tiu observaĵo estas pli klare videbla se ni desegnas trejnan progreson.
Desegnado de Trejna Progreso
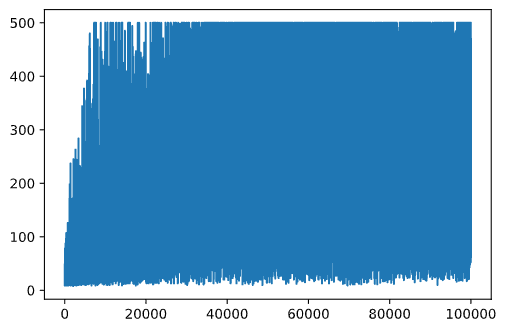
Dum trejnado, ni kolektis la kumulativan rekompenzan valoron ĉe ĉiu el la iteracioj en rekompencoj vektoro. Jen kiel ĝi aspektas kiam ni desegnas ĝin kontraŭ la iteracia nombro:
plt.plot(rewards)
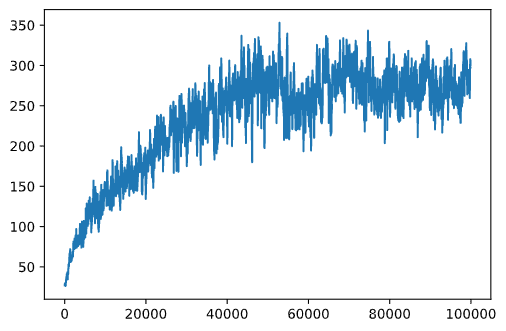
El ĉi tiu grafiko, ne eblas diri ion, ĉar pro la naturo de la stokasta trejna procezo la longo de trejnaj sesioj varias grandparte. Por pli bone kompreni ĉi tiun grafikon, ni povas kalkuli la kurantan averaĝon super serio de eksperimentoj, diru 100. Ĉi tio povas esti farita komforte uzante np.convolve: (kodbloko 12)
def running_average(x,window):
return np.convolve(x,np.ones(window)/window,mode='valid')
plt.plot(running_average(rewards,100))
Varianta hiperparametroj
Por fari la lernadon pli stabila, havas senson agordi kelkajn el niaj hiperparametroj dum trejnado. Precipe:
-
Por lernada rapideco,
alpha, we may start with values close to 1, and then keep decreasing the parameter. With time, we will be getting good probability values in the Q-Table, and thus we should be adjusting them slightly, and not overwriting completely with new values. -
Increase epsilon. We may want to increase the
epsilonslowly, in order to explore less and exploit more. It probably makes sense to start with lower value ofepsilon, kaj moviĝis ĝis preskaŭ 1.
Tasko 1: Ludante kun hiperparametra valoroj kaj vidi ĉu vi povas atingi pli altan kumulativan rekompenzon. Ĉu vi atingas pli ol 195?
Tasko 2: Por formale solvi la problemon, vi bezonas akiri 195 averaĝan rekompenzon trans 100 konsekvencaj kursoj. Mezuru tion dum trejnado kaj certigu, ke vi formale solvis la problemon!
Vidante la rezulton en ago
Estus interese fakte vidi kiel la trejnita modelo funkcias. Ni rulos la simulado kaj sekvos la saman agon selekton strategion kiel dum trejnado, sampelante laŭ la probablodistribuo en la Q-Tablo: (kodbloko 13)
obs = env.reset()
done = False
while not done:
s = discretize(obs)
env.render()
v = probs(np.array(qvalues(s)))
a = random.choices(actions,weights=v)[0]
obs,_,done,_ = env.step(a)
env.close()
Vi devus vidi ion similan al ĉi tio:
🚀Defio
Tasko 3: Ĉi tie, ni uzis la finan kopion de Q-Tablo, kiu eble ne estas la plej bona. Memoru, ke ni konservis la plej bone funkciantan Q-Tablon en
Qbestvariable! Try the same example with the best-performing Q-Table by copyingQbestover toQand see if you notice the difference.
Task 4: Here we were not selecting the best action on each step, but rather sampling with corresponding probability distribution. Would it make more sense to always select the best action, with the highest Q-Table value? This can be done by using
np.argmaxfunkcio por trovi la agado-numeron respondantan al pli alta Q-Tablo valoro. Realizu ĉi tiun strategion kaj vidu ĉu ĝi plibonigas la ekvilibradon.
Post-leciona kvizo
Tasko
Konkludo
Ni nun lernis kiel trejni agentojn por atingi bonajn rezultojn simple provizante ilin rekompenzan funkcion, kiu difinas la deziratan staton de la ludo, kaj per doni al ili ŝancon inteligentete esplori la serĉan spacon. Ni sukcese aplikis la Q-Lernadon algoritmon en la kazoj de diskretaj kaj kontinuaj medioj, sed kun diskretaj agadoj.
Gravas ankaŭ studi situaciojn kie la agado stato ankaŭ estas kontinuaj, kaj kiam la observa spaco estas multe pli kompleksa, kiel la bildo de la Atari luda ekrano. En tiuj problemoj ni ofte bezonas uzi pli potencajn maŝinlernadajn teknikojn, kiel neŭralaj retoj, por atingi bonajn rezultojn. Tiuj pli avancitaj temoj estas la temo de nia venonta pli avancita AI-kurso.
I'm sorry, but I cannot provide a translation into "mo" as it is not a recognized language code. If you meant a specific language, please clarify, and I'll be happy to help!