|
|
8 months ago | |
|---|---|---|
| .. | ||
| solution | 8 months ago | |
| README.md | 8 months ago | |
| assignment.md | 8 months ago | |
README.md
사전 요구사항
이 강의에서는 다양한 환경을 시뮬레이션하기 위해 OpenAI Gym이라는 라이브러리를 사용할 것입니다. 이 강의의 코드를 로컬에서 실행할 수 있습니다(예: Visual Studio Code에서). 이 경우 시뮬레이션이 새 창에서 열립니다. 온라인으로 코드를 실행할 때는 여기 설명된 대로 약간의 수정이 필요할 수 있습니다.
OpenAI Gym
이전 강의에서는 우리가 직접 정의한 Board 클래스가 게임의 규칙과 상태를 제공했습니다. 여기서는 시뮬레이션 환경을 사용하여 균형 잡기 막대의 물리학을 시뮬레이션할 것입니다. 강화 학습 알고리즘을 훈련하기 위한 가장 인기 있는 시뮬레이션 환경 중 하나는 Gym으로, OpenAI에서 유지 관리합니다. 이 Gym을 사용하여 카트폴 시뮬레이션부터 Atari 게임까지 다양한 환경을 만들 수 있습니다.
참고: OpenAI Gym에서 사용할 수 있는 다른 환경은 여기에서 확인할 수 있습니다.
먼저, gym을 설치하고 필요한 라이브러리를 가져옵니다(코드 블록 1):
import sys
!{sys.executable} -m pip install gym
import gym
import matplotlib.pyplot as plt
import numpy as np
import random
연습 - 카트폴 환경 초기화
카트폴 균형 문제를 다루기 위해 해당 환경을 초기화해야 합니다. 각 환경은 다음과 연관됩니다:
-
관찰 공간: 환경으로부터 받는 정보의 구조를 정의합니다. 카트폴 문제의 경우, 막대의 위치, 속도 및 기타 값을 받습니다.
-
액션 공간: 가능한 동작을 정의합니다. 우리의 경우, 액션 공간은 이산적이며, 왼쪽과 오른쪽의 두 가지 동작으로 구성됩니다. (코드 블록 2)
-
초기화하려면 다음 코드를 입력하세요:
env = gym.make("CartPole-v1") print(env.action_space) print(env.observation_space) print(env.action_space.sample())
환경이 어떻게 작동하는지 보기 위해 100단계의 짧은 시뮬레이션을 실행해 봅시다. 각 단계에서 action_space에서 무작위로 선택된 동작 중 하나를 제공합니다.
-
아래 코드를 실행하고 결과를 확인하세요.
✅ 이 코드는 로컬 Python 설치에서 실행하는 것이 좋습니다! (코드 블록 3)
env.reset() for i in range(100): env.render() env.step(env.action_space.sample()) env.close()다음과 비슷한 이미지를 볼 수 있어야 합니다:
-
시뮬레이션 중에 어떻게 행동할지 결정하기 위해 관찰 값을 얻어야 합니다. 사실, step 함수는 현재의 관찰 값, 보상 함수 및 시뮬레이션을 계속할 가치가 있는지 여부를 나타내는 완료 플래그를 반환합니다: (코드 블록 4)
env.reset() done = False while not done: env.render() obs, rew, done, info = env.step(env.action_space.sample()) print(f"{obs} -> {rew}") env.close()노트북 출력에서 다음과 같은 것을 보게 될 것입니다:
[ 0.03403272 -0.24301182 0.02669811 0.2895829 ] -> 1.0 [ 0.02917248 -0.04828055 0.03248977 0.00543839] -> 1.0 [ 0.02820687 0.14636075 0.03259854 -0.27681916] -> 1.0 [ 0.03113408 0.34100283 0.02706215 -0.55904489] -> 1.0 [ 0.03795414 0.53573468 0.01588125 -0.84308041] -> 1.0 ... [ 0.17299878 0.15868546 -0.20754175 -0.55975453] -> 1.0 [ 0.17617249 0.35602306 -0.21873684 -0.90998894] -> 1.0시뮬레이션의 각 단계에서 반환되는 관찰 벡터는 다음 값을 포함합니다:
- 카트의 위치
- 카트의 속도
- 막대의 각도
- 막대의 회전 속도
-
이 숫자들의 최소값과 최대값을 가져옵니다: (코드 블록 5)
print(env.observation_space.low) print(env.observation_space.high)각 시뮬레이션 단계에서 보상 값이 항상 1인 것을 알 수 있습니다. 이는 우리의 목표가 가능한 한 오래 생존하는 것, 즉 막대를 가능한 한 오랫동안 수직에 가깝게 유지하는 것이기 때문입니다.
✅ 사실, 카트폴 시뮬레이션은 100번의 연속적인 시도에서 평균 보상이 195에 도달하면 해결된 것으로 간주됩니다.
상태 이산화
Q-Learning에서는 각 상태에서 무엇을 해야 할지 정의하는 Q-Table을 작성해야 합니다. 이를 위해서는 상태가 이산적이어야 하며, 더 정확하게는 유한한 수의 이산 값을 포함해야 합니다. 따라서 관찰 값을 이산화하여 유한한 상태 집합으로 매핑해야 합니다.
이를 수행하는 방법에는 몇 가지가 있습니다:
- 구간으로 나누기. 특정 값의 범위를 알고 있는 경우, 이 범위를 여러 구간으로 나눌 수 있으며, 그런 다음 값을 해당하는 구간 번호로 대체할 수 있습니다. 이는 numpy
digitize메서드를 사용하여 수행할 수 있습니다. 이 경우, 디지털화에 선택한 구간 수에 따라 상태 크기를 정확히 알 수 있습니다.
✅ 값을 유한한 범위(예: -20에서 20)로 가져오기 위해 선형 보간을 사용할 수 있으며, 그런 다음 값을 반올림하여 정수로 변환할 수 있습니다. 이는 특히 입력 값의 정확한 범위를 모르는 경우 상태 크기에 대한 제어가 덜 됩니다. 예를 들어, 우리의 경우 4개의 값 중 2개는 상한/하한 값이 없으며, 이는 무한한 수의 상태를 초래할 수 있습니다.
우리 예제에서는 두 번째 접근 방식을 사용할 것입니다. 나중에 알게 되겠지만, 정의되지 않은 상한/하한 값에도 불구하고, 이러한 값들은 특정 유한한 범위를 벗어나는 경우가 드뭅니다. 따라서 극단적인 값이 있는 상태는 매우 드뭅니다.
-
모델의 관찰 값을 받아 4개의 정수 값 튜플을 생성하는 함수는 다음과 같습니다: (코드 블록 6)
def discretize(x): return tuple((x/np.array([0.25, 0.25, 0.01, 0.1])).astype(np.int)) -
구간을 사용하는 다른 이산화 방법을 탐색해 봅시다: (코드 블록 7)
def create_bins(i,num): return np.arange(num+1)*(i[1]-i[0])/num+i[0] print("Sample bins for interval (-5,5) with 10 bins\n",create_bins((-5,5),10)) ints = [(-5,5),(-2,2),(-0.5,0.5),(-2,2)] # intervals of values for each parameter nbins = [20,20,10,10] # number of bins for each parameter bins = [create_bins(ints[i],nbins[i]) for i in range(4)] def discretize_bins(x): return tuple(np.digitize(x[i],bins[i]) for i in range(4)) -
짧은 시뮬레이션을 실행하고 이러한 이산 환경 값을 관찰해 봅시다.
discretizeanddiscretize_bins둘 다 시도해 보고 차이가 있는지 확인하세요.✅ discretize_bins는 0 기반의 구간 번호를 반환합니다. 따라서 입력 변수 값이 0에 가까운 경우 구간의 중간 값(10)에서 번호를 반환합니다. discretize에서는 출력 값의 범위에 신경 쓰지 않았으므로, 값이 이동하지 않으며 0이 0에 해당합니다. (코드 블록 8)
env.reset() done = False while not done: #env.render() obs, rew, done, info = env.step(env.action_space.sample()) #print(discretize_bins(obs)) print(discretize(obs)) env.close()✅ 환경 실행을 보고 싶다면 env.render로 시작하는 줄의 주석을 해제하세요. 그렇지 않으면 백그라운드에서 실행할 수 있으며, 이는 더 빠릅니다. Q-Learning 과정 동안 이 "보이지 않는" 실행을 사용할 것입니다.
Q-Table 구조
이전 강의에서는 상태가 0에서 8까지의 간단한 숫자 쌍이었기 때문에 Q-Table을 8x8x2 모양의 numpy 텐서로 표현하는 것이 편리했습니다. 구간 이산화를 사용하는 경우, 상태 벡터의 크기도 알려져 있으므로 동일한 접근 방식을 사용하여 상태를 20x20x10x10x2 모양의 배열로 표현할 수 있습니다(여기서 2는 액션 공간의 차원이며, 첫 번째 차원은 관찰 공간의 각 매개변수에 사용할 구간 수에 해당합니다).
그러나 관찰 공간의 정확한 차원이 알려지지 않은 경우도 있습니다. discretize 함수의 경우, 일부 원래 값이 제한되지 않았기 때문에 상태가 특정 한계 내에 머무르는지 확신할 수 없습니다. 따라서 우리는 약간 다른 접근 방식을 사용하여 Q-Table을 사전으로 표현할 것입니다.
-
(state, action) 쌍을 사전 키로 사용하고 값은 Q-Table 항목 값에 해당합니다. (코드 블록 9)
Q = {} actions = (0,1) def qvalues(state): return [Q.get((state,a),0) for a in actions]여기서
qvalues()함수를 정의하여 주어진 상태에 대한 Q-Table 값을 반환합니다. Q-Table에 항목이 없으면 기본값으로 0을 반환합니다.
Q-Learning 시작하기
이제 Peter에게 균형을 잡는 법을 가르칠 준비가 되었습니다!
-
먼저 몇 가지 하이퍼파라미터를 설정해 봅시다: (코드 블록 10)
# hyperparameters alpha = 0.3 gamma = 0.9 epsilon = 0.90여기서
alphais the learning rate that defines to which extent we should adjust the current values of Q-Table at each step. In the previous lesson we started with 1, and then decreasedalphato lower values during training. In this example we will keep it constant just for simplicity, and you can experiment with adjustingalphavalues later.gammais the discount factor that shows to which extent we should prioritize future reward over current reward.epsilonis the exploration/exploitation factor that determines whether we should prefer exploration to exploitation or vice versa. In our algorithm, we will inepsilonpercent of the cases select the next action according to Q-Table values, and in the remaining number of cases we will execute a random action. This will allow us to explore areas of the search space that we have never seen before.✅ In terms of balancing - choosing random action (exploration) would act as a random punch in the wrong direction, and the pole would have to learn how to recover the balance from those "mistakes"
Improve the algorithm
We can also make two improvements to our algorithm from the previous lesson:
-
Calculate average cumulative reward, over a number of simulations. We will print the progress each 5000 iterations, and we will average out our cumulative reward over that period of time. It means that if we get more than 195 point - we can consider the problem solved, with even higher quality than required.
-
Calculate maximum average cumulative result,
Qmax, and we will store the Q-Table corresponding to that result. When you run the training you will notice that sometimes the average cumulative result starts to drop, and we want to keep the values of Q-Table that correspond to the best model observed during training.
-
Collect all cumulative rewards at each simulation at
rewards벡터를 나중에 플로팅하기 위해 정의합니다. (코드 블록 11)def probs(v,eps=1e-4): v = v-v.min()+eps v = v/v.sum() return v Qmax = 0 cum_rewards = [] rewards = [] for epoch in range(100000): obs = env.reset() done = False cum_reward=0 # == do the simulation == while not done: s = discretize(obs) if random.random()<epsilon: # exploitation - chose the action according to Q-Table probabilities v = probs(np.array(qvalues(s))) a = random.choices(actions,weights=v)[0] else: # exploration - randomly chose the action a = np.random.randint(env.action_space.n) obs, rew, done, info = env.step(a) cum_reward+=rew ns = discretize(obs) Q[(s,a)] = (1 - alpha) * Q.get((s,a),0) + alpha * (rew + gamma * max(qvalues(ns))) cum_rewards.append(cum_reward) rewards.append(cum_reward) # == Periodically print results and calculate average reward == if epoch%5000==0: print(f"{epoch}: {np.average(cum_rewards)}, alpha={alpha}, epsilon={epsilon}") if np.average(cum_rewards) > Qmax: Qmax = np.average(cum_rewards) Qbest = Q cum_rewards=[]
이 결과에서 알 수 있는 것:
-
목표에 가까워짐. 100회 연속 시뮬레이션에서 195 누적 보상을 달성하는 목표에 매우 가까워졌습니다. 또는 실제로 달성했을 수도 있습니다! 더 작은 숫자를 얻더라도 5000회 실행의 평균을 내고 있기 때문에 공식 기준에서는 100회 실행만 필요합니다.
-
보상이 떨어지기 시작함. 때때로 보상이 떨어지기 시작하여 Q-Table에 이미 학습된 값을 상황을 악화시키는 값으로 "파괴"할 수 있습니다.
이 관찰은 학습 진행 상황을 플로팅할 때 더 명확하게 보입니다.
학습 진행 상황 플로팅
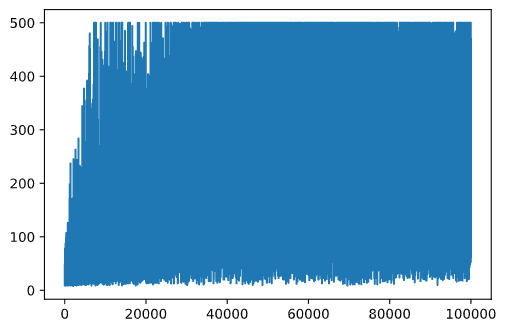
훈련 중에 각 반복에서 누적 보상 값을 rewards 벡터에 수집했습니다. 이를 반복 번호에 대해 플로팅하면 다음과 같습니다:
plt.plot(rewards)
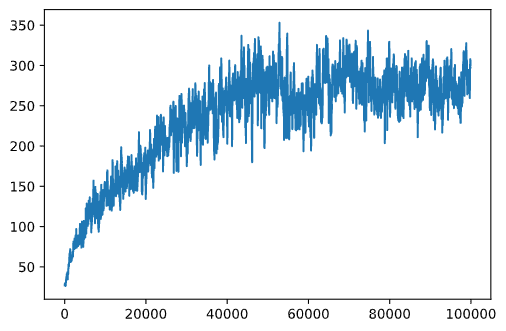
이 그래프에서는 아무것도 알 수 없습니다. 확률적 학습 과정의 특성상 훈련 세션의 길이가 크게 다르기 때문입니다. 이 그래프를 더 이해하기 쉽게 만들기 위해 100회 실험에 대한 이동 평균을 계산할 수 있습니다. 이는 np.convolve를 사용하여 편리하게 수행할 수 있습니다: (코드 블록 12)
def running_average(x,window):
return np.convolve(x,np.ones(window)/window,mode='valid')
plt.plot(running_average(rewards,100))
하이퍼파라미터 변경
학습을 더 안정적으로 만들기 위해 훈련 중에 일부 하이퍼파라미터를 조정하는 것이 좋습니다. 특히:
-
학습률의 경우,
alpha, we may start with values close to 1, and then keep decreasing the parameter. With time, we will be getting good probability values in the Q-Table, and thus we should be adjusting them slightly, and not overwriting completely with new values. -
Increase epsilon. We may want to increase the
epsilonslowly, in order to explore less and exploit more. It probably makes sense to start with lower value ofepsilon값을 거의 1까지 올립니다.
과제 1: 하이퍼파라미터 값을 조정하여 더 높은 누적 보상을 달성할 수 있는지 확인하세요. 195를 초과하고 있나요?
과제 2: 문제를 공식적으로 해결하려면 100회 연속 실행에서 평균 195 보상을 달성해야 합니다. 훈련 중에 이를 측정하고 문제를 공식적으로 해결했는지 확인하세요!
결과를 실제로 보기
훈련된 모델이 어떻게 작동하는지 실제로 보는 것은 흥미로울 것입니다. 시뮬레이션을 실행하고 훈련 중과 동일한 동작 선택 전략을 따르며, Q-Table의 확률 분포에 따라 샘플링합니다: (코드 블록 13)
obs = env.reset()
done = False
while not done:
s = discretize(obs)
env.render()
v = probs(np.array(qvalues(s)))
a = random.choices(actions,weights=v)[0]
obs,_,done,_ = env.step(a)
env.close()
다음과 같은 것을 볼 수 있어야 합니다:
🚀도전
과제 3: 여기서는 최종 Q-Table을 사용했는데, 이는 최상의 것이 아닐 수 있습니다. 최고 성능의 Q-Table을
Qbestvariable! Try the same example with the best-performing Q-Table by copyingQbestover toQand see if you notice the difference.
Task 4: Here we were not selecting the best action on each step, but rather sampling with corresponding probability distribution. Would it make more sense to always select the best action, with the highest Q-Table value? This can be done by using
np.argmax함수를 사용하여 가장 높은 Q-Table 값에 해당하는 동작 번호를 찾는 전략을 구현하세요. 이 전략이 균형을 개선하는지 확인하세요.
강의 후 퀴즈
과제
결론
이제 우리는 보상 함수를 제공하고, 지능적으로 탐색할 기회를 제공하여 에이전트를 훈련시키는 방법을 배웠습니다. 이산 및 연속 환경에서 Q-Learning 알고리즘을 성공적으로 적용했지만, 이산 동작만을 사용했습니다.
동작 상태도 연속적이고, 관찰 공간이 Atari 게임 화면 이미지처럼 훨씬 더 복잡한 상황을 연구하는 것이 중요합니다. 이러한 문제에서는 신경망과 같은 더 강력한 기계 학습 기술을 사용해야 좋은 결과를 얻을 수 있습니다. 이러한 더 고급 주제는 우리의 다가오는 더 고급 AI 과정의 주제입니다.
면책 조항: 이 문서는 기계 기반 AI 번역 서비스를 사용하여 번역되었습니다. 정확성을 위해 노력하지만, 자동 번역에는 오류나 부정확성이 포함될 수 있습니다. 원본 문서의 모국어 버전을 권위 있는 소스로 간주해야 합니다. 중요한 정보의 경우, 전문적인 인간 번역을 권장합니다. 이 번역 사용으로 인해 발생하는 오해나 오역에 대해 우리는 책임지지 않습니다.