|
|
8 months ago | |
|---|---|---|
| .. | ||
| solution | 8 months ago | |
| README.md | 8 months ago | |
| assignment.md | 8 months ago | |
README.md
カートポール スケート
前回のレッスンで解決していた問題は、現実のシナリオには適用できないおもちゃの問題のように見えるかもしれません。しかし、実際には多くの現実の問題もこのシナリオを共有しています。例えば、チェスや囲碁のプレイも同様です。これらは、与えられたルールと離散状態を持つボードがあるため、似ています。
講義前クイズ
はじめに
このレッスンでは、連続状態を持つ問題にQラーニングの原則を適用します。連続状態とは、1つ以上の実数で与えられる状態のことです。以下の問題に取り組みます:
問題: ピーターが狼から逃げるためには、もっと速く動けるようになる必要があります。Qラーニングを使用して、ピーターがスケートを学び、特にバランスを保つ方法を見てみましょう。
ピーターと彼の友達は、狼から逃れるために創造的になります!画像はJen Looperによるものです。
ここでは、カートポール問題として知られるバランスを取る方法の簡略版を使用します。カートポールの世界では、左右に動ける水平スライダーがあり、その上に垂直のポールをバランスさせることが目標です。
前提条件
このレッスンでは、OpenAI Gymというライブラリを使用して、さまざまな環境をシミュレートします。このレッスンのコードをローカル(例:Visual Studio Code)で実行する場合、シミュレーションは新しいウィンドウで開きます。オンラインでコードを実行する場合は、こちらに記載されているように、コードにいくつかの調整が必要になるかもしれません。
OpenAI Gym
前回のレッスンでは、ゲームのルールと状態は自分で定義したBoardクラスによって与えられました。ここでは、バランスポールの物理をシミュレートする特別なシミュレーション環境を使用します。強化学習アルゴリズムをトレーニングするための最も人気のあるシミュレーション環境の1つは、Gymと呼ばれ、OpenAIによって維持されています。このジムを使用することで、カートポールシミュレーションからアタリゲームまで、さまざまな環境を作成できます。
Note: OpenAI Gymで利用可能な他の環境はこちらで確認できます。
まず、ジムをインストールし、必要なライブラリをインポートしましょう(コードブロック1):
import sys
!{sys.executable} -m pip install gym
import gym
import matplotlib.pyplot as plt
import numpy as np
import random
演習 - カートポール環境の初期化
カートポールのバランス問題に取り組むために、対応する環境を初期化する必要があります。各環境には次のものが関連付けられています:
-
観察スペース: 環境から受け取る情報の構造を定義します。カートポール問題では、ポールの位置、速度、およびその他の値を受け取ります。
-
アクションスペース: 可能なアクションを定義します。私たちの場合、アクションスペースは離散的で、左と右の2つのアクションから成ります。(コードブロック2)
-
初期化するために、次のコードを入力します:
env = gym.make("CartPole-v1") print(env.action_space) print(env.observation_space) print(env.action_space.sample())
環境がどのように機能するかを見るために、100ステップの短いシミュレーションを実行してみましょう。各ステップで、取るべきアクションの1つを提供します。このシミュレーションでは、action_spaceからランダムにアクションを選択します。
-
以下のコードを実行して、その結果を確認してください。
✅ このコードをローカルのPythonインストールで実行することが推奨されます!(コードブロック3)
env.reset() for i in range(100): env.render() env.step(env.action_space.sample()) env.close()次のような画像が表示されるはずです:
-
シミュレーション中に、どのように行動するかを決定するために観察を取得する必要があります。実際、ステップ関数は現在の観察、報酬関数、およびシミュレーションを続行するかどうかを示す完了フラグを返します:(コードブロック4)
env.reset() done = False while not done: env.render() obs, rew, done, info = env.step(env.action_space.sample()) print(f"{obs} -> {rew}") env.close()ノートブックの出力に次のようなものが表示されるはずです:
[ 0.03403272 -0.24301182 0.02669811 0.2895829 ] -> 1.0 [ 0.02917248 -0.04828055 0.03248977 0.00543839] -> 1.0 [ 0.02820687 0.14636075 0.03259854 -0.27681916] -> 1.0 [ 0.03113408 0.34100283 0.02706215 -0.55904489] -> 1.0 [ 0.03795414 0.53573468 0.01588125 -0.84308041] -> 1.0 ... [ 0.17299878 0.15868546 -0.20754175 -0.55975453] -> 1.0 [ 0.17617249 0.35602306 -0.21873684 -0.90998894] -> 1.0シミュレーションの各ステップで返される観察ベクトルには次の値が含まれます:
- カートの位置
- カートの速度
- ポールの角度
- ポールの回転率
-
これらの数値の最小値と最大値を取得します:(コードブロック5)
print(env.observation_space.low) print(env.observation_space.high)また、各シミュレーションステップでの報酬値が常に1であることに気付くかもしれません。これは、私たちの目標ができるだけ長く生存し、ポールを垂直に保つことであるためです。
✅ 実際、カートポールシミュレーションは、100回連続の試行で平均報酬が195に達した場合に解決されたと見なされます。
状態の離散化
Qラーニングでは、各状態で何をするかを定義するQテーブルを構築する必要があります。これを行うためには、状態が離散的である必要があります。つまり、有限の離散値を含む必要があります。したがって、観察を離散化し、有限の状態セットにマッピングする必要があります。
これを行う方法はいくつかあります:
- ビンに分割する。特定の値の範囲がわかっている場合、この範囲をいくつかのビンに分割し、その値が属するビン番号で置き換えることができます。これはnumpyの
digitizeメソッドを使用して行うことができます。この場合、デジタル化に選択したビンの数に依存するため、状態サイズが正確にわかります。
✅ 線形補間を使用して値をある有限の範囲(例えば、-20から20)に持ってきてから、四捨五入して整数に変換することもできます。これにより、入力値の正確な範囲がわからない場合でも、状態サイズに対する制御が少なくなります。例えば、私たちの場合、4つの値のうち2つは上限/下限がありません。これにより、無限の状態数が発生する可能性があります。
この例では、2番目のアプローチを使用します。後で気づくかもしれませんが、定義されていない上限/下限にもかかわらず、これらの値は特定の有限の範囲外に出ることはめったにありません。そのため、極端な値を持つ状態は非常にまれです。
-
次の関数は、モデルからの観察を取り、4つの整数値のタプルを生成します:(コードブロック6)
def discretize(x): return tuple((x/np.array([0.25, 0.25, 0.01, 0.1])).astype(np.int)) -
もう1つのビンを使用した離散化方法も探索しましょう:(コードブロック7)
def create_bins(i,num): return np.arange(num+1)*(i[1]-i[0])/num+i[0] print("Sample bins for interval (-5,5) with 10 bins\n",create_bins((-5,5),10)) ints = [(-5,5),(-2,2),(-0.5,0.5),(-2,2)] # intervals of values for each parameter nbins = [20,20,10,10] # number of bins for each parameter bins = [create_bins(ints[i],nbins[i]) for i in range(4)] def discretize_bins(x): return tuple(np.digitize(x[i],bins[i]) for i in range(4)) -
次に、短いシミュレーションを実行し、それらの離散環境値を観察しましょう。
discretizeanddiscretize_binsの両方を試してみて、違いがあるかどうかを確認してください。✅ discretize_binsはビン番号を返しますが、これは0ベースです。したがって、入力変数の値が0に近い場合、範囲の中央(10)の数を返します。discretizeでは、出力値の範囲を気にしなかったため、値はシフトされず、0は0に対応します。(コードブロック8)
env.reset() done = False while not done: #env.render() obs, rew, done, info = env.step(env.action_space.sample()) #print(discretize_bins(obs)) print(discretize(obs)) env.close()✅ 環境が実行される様子を見たい場合は、env.renderで始まる行のコメントを外してください。そうでない場合は、バックグラウンドで実行することができ、これにより高速化されます。この「見えない」実行をQラーニングプロセス中に使用します。
Q-テーブルの構造
前回のレッスンでは、状態は0から8までの単純な数字のペアであり、そのためQ-テーブルを8x8x2の形状のnumpyテンソルで表現するのが便利でした。ビンの離散化を使用する場合、状態ベクトルのサイズもわかっているため、同じアプローチを使用し、観察スペースの各パラメータに使用するビンの数に対応する形状の配列(20x20x10x10x2)で状態を表現できます。
しかし、観察スペースの正確な次元がわからない場合もあります。discretize関数の場合、元の値の一部が制限されていないため、状態が特定の制限内に収まることを保証できません。そのため、Q-テーブルを辞書で表現するという異なるアプローチを使用します。
-
辞書キーとして*(state,action)*のペアを使用し、値はQ-テーブルのエントリ値に対応します。(コードブロック9)
Q = {} actions = (0,1) def qvalues(state): return [Q.get((state,a),0) for a in actions]ここでは、特定の状態に対するすべての可能なアクションに対応するQ-テーブル値のリストを返す
qvalues()関数も定義します。Q-テーブルにエントリが存在しない場合、デフォルトで0を返します。
Qラーニングを始めましょう
さて、ピーターにバランスを取ることを教える準備ができました!
-
まず、いくつかのハイパーパラメータを設定しましょう:(コードブロック10)
# hyperparameters alpha = 0.3 gamma = 0.9 epsilon = 0.90ここで、
alphais the learning rate that defines to which extent we should adjust the current values of Q-Table at each step. In the previous lesson we started with 1, and then decreasedalphato lower values during training. In this example we will keep it constant just for simplicity, and you can experiment with adjustingalphavalues later.gammais the discount factor that shows to which extent we should prioritize future reward over current reward.epsilonis the exploration/exploitation factor that determines whether we should prefer exploration to exploitation or vice versa. In our algorithm, we will inepsilonpercent of the cases select the next action according to Q-Table values, and in the remaining number of cases we will execute a random action. This will allow us to explore areas of the search space that we have never seen before.✅ In terms of balancing - choosing random action (exploration) would act as a random punch in the wrong direction, and the pole would have to learn how to recover the balance from those "mistakes"
Improve the algorithm
We can also make two improvements to our algorithm from the previous lesson:
-
Calculate average cumulative reward, over a number of simulations. We will print the progress each 5000 iterations, and we will average out our cumulative reward over that period of time. It means that if we get more than 195 point - we can consider the problem solved, with even higher quality than required.
-
Calculate maximum average cumulative result,
Qmax, and we will store the Q-Table corresponding to that result. When you run the training you will notice that sometimes the average cumulative result starts to drop, and we want to keep the values of Q-Table that correspond to the best model observed during training.
-
Collect all cumulative rewards at each simulation at
rewardsベクトルに収集しました。これを後でプロットするために使用します。(コードブロック11)def probs(v,eps=1e-4): v = v-v.min()+eps v = v/v.sum() return v Qmax = 0 cum_rewards = [] rewards = [] for epoch in range(100000): obs = env.reset() done = False cum_reward=0 # == do the simulation == while not done: s = discretize(obs) if random.random()<epsilon: # exploitation - chose the action according to Q-Table probabilities v = probs(np.array(qvalues(s))) a = random.choices(actions,weights=v)[0] else: # exploration - randomly chose the action a = np.random.randint(env.action_space.n) obs, rew, done, info = env.step(a) cum_reward+=rew ns = discretize(obs) Q[(s,a)] = (1 - alpha) * Q.get((s,a),0) + alpha * (rew + gamma * max(qvalues(ns))) cum_rewards.append(cum_reward) rewards.append(cum_reward) # == Periodically print results and calculate average reward == if epoch%5000==0: print(f"{epoch}: {np.average(cum_rewards)}, alpha={alpha}, epsilon={epsilon}") if np.average(cum_rewards) > Qmax: Qmax = np.average(cum_rewards) Qbest = Q cum_rewards=[]
結果から次のことがわかります:
-
目標に近い。100回以上の連続シミュレーションで195の累積報酬を得るという目標に非常に近づいているか、実際に達成しているかもしれません!小さな数値を得ても、5000回の実行で平均しているため、正式な基準では100回の実行のみが必要です。
-
報酬が低下し始める。時々、報酬が低下し始めることがあります。これは、Q-テーブルに既に学習した値を破壊し、状況を悪化させる値を新たに追加していることを意味します。
この観察は、トレーニングの進捗をプロットするとより明確に見えます。
トレーニングの進捗をプロットする
トレーニング中、各イテレーションで累積報酬値をrewardsベクトルに収集しました。これをイテレーション番号に対してプロットすると次のようになります:
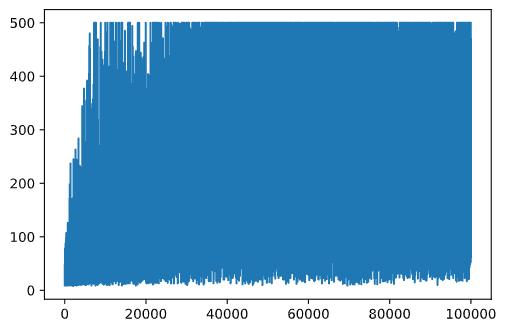
plt.plot(rewards)
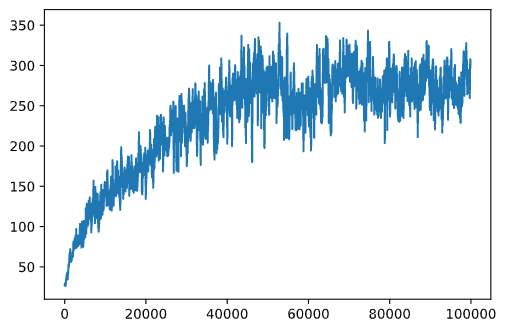
このグラフからは何もわかりません。これは、確率的トレーニングプロセスの性質上、トレーニングセッションの長さが大きく異なるためです。このグラフをより理解しやすくするために、一連の実験(例えば100)の移動平均を計算できます。これはnp.convolveを使用して便利に行うことができます:(コードブロック12)
def running_average(x,window):
return np.convolve(x,np.ones(window)/window,mode='valid')
plt.plot(running_average(rewards,100))
ハイパーパラメータの変更
学習をより安定させるために、トレーニング中にいくつかのハイパーパラメータを調整することが理にかなっています。特に:
-
学習率に関しては、
alpha, we may start with values close to 1, and then keep decreasing the parameter. With time, we will be getting good probability values in the Q-Table, and thus we should be adjusting them slightly, and not overwriting completely with new values. -
Increase epsilon. We may want to increase the
epsilonslowly, in order to explore less and exploit more. It probably makes sense to start with lower value ofepsilonの値を徐々に減少させ、ほぼ1に近づけます。
Task 1: ハイパーパラメータの値を変更して、より高い累積報酬を達成できるか試してみてください。195以上を達成していますか?
Task 2: 問題を正式に解決するには、100回連続の実行で平均195の報酬を得る必要があります。トレーニング中にそれを測定し、問題を正式に解決したことを確認してください!
結果を実際に見る
トレーニングされたモデルがどのように動作するかを実際に見ることは興味深いでしょう。シミュレーションを実行し、トレーニング中と同じアクション選択戦略に従い、Q-テーブルの確率分布に基づいてサンプリングします:(コードブロック13)
obs = env.reset()
done = False
while not done:
s = discretize(obs)
env.render()
v = probs(np.array(qvalues(s)))
a = random.choices(actions,weights=v)[0]
obs,_,done,_ = env.step(a)
env.close()
次のようなものが表示されるはずです:
🚀チャレンジ
Task 3: ここでは、Q-テーブルの最終コピーを使用しましたが、これが最良のものとは限りません。最もパフォーマンスの良いQ-テーブルを
Qbestvariable! Try the same example with the best-performing Q-Table by copyingQbestover toQand see if you notice the difference.
Task 4: Here we were not selecting the best action on each step, but rather sampling with corresponding probability distribution. Would it make more sense to always select the best action, with the highest Q-Table value? This can be done by using
np.argmax関数を使用して、最も高いQ-テーブル値に対応するアクション番号を見つける戦略を実装し、それがバランスを改善するかどうかを確認してください。
講義後クイズ
課題
結論
私たちは、エージェントに報酬関数を提供し、ゲームの望ましい状態を定義し、探索空間を知的に探索する機会を与えることで、良い結果を達成する方法を学びました。私たちは、離散的および連続的な環境でQラーニングアルゴリズムを成功裏に適用しましたが、アクションは離散的なままでした。
アクション状態も連続している場合や、観察スペースがアタリゲーム画面の画像のように非常に複雑な場合もあります。これらの問題では、良い結果を得るために、ニューラルネットワークなどのより強力な機械学習技術を使用する必要があります。これらのより高度なトピックは、今後のより高度なAIコースの主題となります。
免責事項: この文書は、機械ベースのAI翻訳サービスを使用して翻訳されています。正確さを期していますが、自動翻訳には誤りや不正確さが含まれる場合があります。元の言語で書かれた原文が権威ある情報源と見なされるべきです。重要な情報については、専門の人間による翻訳をお勧めします。この翻訳の使用に起因する誤解や誤訳について、当社は責任を負いません。