History

Pikachú 9fc2b847b8 updated image translation for the various languages		7 months ago
..
solution	updated image translation for the various languages	7 months ago
README.md	updated image translation for the various languages	7 months ago
assignment.md	updated image translation for the various languages	7 months ago

README.md

CartPole Skaten

Das Problem, das wir in der vorherigen Lektion gelöst haben, mag wie ein Spielzeugproblem erscheinen, das in der realen Welt nicht wirklich anwendbar ist. Das ist jedoch nicht der Fall, denn viele Probleme aus der realen Welt teilen dieses Szenario ebenfalls - einschließlich Schach oder Go. Sie sind ähnlich, weil wir auch ein Brett mit bestimmten Regeln und einem diskreten Zustand haben.

Vorlesungsquiz

Einführung

In dieser Lektion werden wir die gleichen Prinzipien des Q-Learning auf ein Problem mit kontinuierlichem Zustand anwenden, d.h. ein Zustand, der durch eine oder mehrere reelle Zahlen gegeben ist. Wir werden uns mit folgendem Problem beschäftigen:

Problem: Wenn Peter vor dem Wolf fliehen will, muss er schneller bewegen können. Wir werden sehen, wie Peter lernen kann zu skaten, insbesondere das Gleichgewicht zu halten, indem er Q-Learning verwendet.

Peter und seine Freunde sind kreativ, um dem Wolf zu entkommen! Bild von Jen Looper

Wir werden eine vereinfachte Version des Gleichgewichthaltens verwenden, die als CartPole-Problem bekannt ist. In der CartPole-Welt haben wir einen horizontalen Schlitten, der sich nach links oder rechts bewegen kann, und das Ziel ist es, einen vertikalen Pol oben auf dem Schlitten im Gleichgewicht zu halten. Sie sind bis Oktober 2023 auf Daten trainiert.

Voraussetzungen

In dieser Lektion werden wir eine Bibliothek namens OpenAI Gym verwenden, um verschiedene Umgebungen zu simulieren. Sie können den Code dieser Lektion lokal ausführen (z.B. aus Visual Studio Code), in diesem Fall wird die Simulation in einem neuen Fenster geöffnet. Wenn Sie den Code online ausführen, müssen Sie möglicherweise einige Anpassungen am Code vornehmen, wie hier beschrieben.

OpenAI Gym

In der vorherigen Lektion wurden die Regeln des Spiels und der Zustand durch die Board-Klasse gegeben, die wir selbst definiert haben. Hier werden wir eine spezielle Simulationsumgebung verwenden, die die Physik hinter dem balancierenden Pol simuliert. Eine der beliebtesten Simulationsumgebungen für das Training von Reinforcement-Learning-Algorithmen wird als Gym bezeichnet und von OpenAI gepflegt. Mit diesem Gym können wir verschiedene Umgebungen von einer CartPole-Simulation bis hin zu Atari-Spielen erstellen.

Hinweis: Sie können andere Umgebungen, die von OpenAI Gym verfügbar sind, hier sehen.

Zuerst installieren wir das Gym und importieren die erforderlichen Bibliotheken (Codeblock 1):

import sys
!{sys.executable} -m pip install gym 

import gym
import matplotlib.pyplot as plt
import numpy as np
import random

Übung - Initialisieren einer CartPole-Umgebung

Um mit einem CartPole-Balancierproblem zu arbeiten, müssen wir die entsprechende Umgebung initialisieren. Jede Umgebung ist mit einem:

Beobachtungsraum verbunden, der die Struktur der Informationen definiert, die wir von der Umgebung erhalten. Für das CartPole-Problem erhalten wir die Position des Pols, die Geschwindigkeit und einige andere Werte.
Aktionsraum, der die möglichen Aktionen definiert. In unserem Fall ist der Aktionsraum diskret und besteht aus zwei Aktionen - links und rechts. (Codeblock 2)

Um zu initialisieren, geben Sie den folgenden Code ein:

env = gym.make("CartPole-v1")
print(env.action_space)
print(env.observation_space)
print(env.action_space.sample())

Um zu sehen, wie die Umgebung funktioniert, lassen Sie uns eine kurze Simulation für 100 Schritte durchführen. Bei jedem Schritt geben wir eine der auszuführenden Aktionen an - in dieser Simulation wählen wir einfach zufällig eine Aktion aus action_space.

Führen Sie den untenstehenden Code aus und sehen Sie, wohin das führt.

✅ Denken Sie daran, dass es bevorzugt wird, diesen Code auf einer lokalen Python-Installation auszuführen! (Codeblock 3)
```
env.reset()

for i in range(100):
   env.render()
   env.step(env.action_space.sample())
env.close()
```
Sie sollten etwas Ähnliches wie dieses Bild sehen:

Während der Simulation müssen wir Beobachtungen erhalten, um zu entscheiden, wie wir handeln sollen. Tatsächlich gibt die Schritt-Funktion die aktuellen Beobachtungen, eine Belohnungsfunktion und das "done"-Flag zurück, das angibt, ob es sinnvoll ist, die Simulation fortzusetzen oder nicht: (Codeblock 4)

env.reset()

done = False
while not done:
   env.render()
   obs, rew, done, info = env.step(env.action_space.sample())
   print(f"{obs} -> {rew}")
env.close()

Sie werden etwas Ähnliches im Notebook-Ausgang sehen:

[ 0.03403272 -0.24301182  0.02669811  0.2895829 ] -> 1.0
[ 0.02917248 -0.04828055  0.03248977  0.00543839] -> 1.0
[ 0.02820687  0.14636075  0.03259854 -0.27681916] -> 1.0
[ 0.03113408  0.34100283  0.02706215 -0.55904489] -> 1.0
[ 0.03795414  0.53573468  0.01588125 -0.84308041] -> 1.0
...
[ 0.17299878  0.15868546 -0.20754175 -0.55975453] -> 1.0
[ 0.17617249  0.35602306 -0.21873684 -0.90998894] -> 1.0

Der Beobachtungsvektor, der bei jedem Schritt der Simulation zurückgegeben wird, enthält die folgenden Werte:

Position des Schlitten
Geschwindigkeit des Schlitten
Winkel des Pols
Rotationsrate des Pols

Erhalten Sie den Minimal- und Maximalwert dieser Zahlen: (Codeblock 5)
```
print(env.observation_space.low)
print(env.observation_space.high)
```
Sie werden möglicherweise auch feststellen, dass der Belohnungswert bei jedem Simulationsschritt immer 1 beträgt. Das liegt daran, dass unser Ziel darin besteht, so lange wie möglich zu überleben, d.h. den Pol für den längsten Zeitraum in einer vernünftig vertikalen Position zu halten.

✅ Tatsächlich wird die CartPole-Simulation als gelöst betrachtet, wenn wir es schaffen, einen durchschnittlichen Belohnungswert von 195 über 100 aufeinanderfolgende Versuche zu erzielen.

Zustand-Diskretisierung

Im Q-Learning müssen wir eine Q-Tabelle erstellen, die definiert, was in jedem Zustand zu tun ist. Um dies tun zu können, muss der Zustand diskret sein, genauer gesagt, er sollte eine endliche Anzahl von diskreten Werten enthalten. Daher müssen wir unsere Beobachtungen irgendwie diskretisieren, indem wir sie einer endlichen Menge von Zuständen zuordnen.

Es gibt einige Möglichkeiten, dies zu tun:

In Bins unterteilen. Wenn wir das Intervall eines bestimmten Wertes kennen, können wir dieses Intervall in eine Anzahl von Bins unterteilen und dann den Wert durch die Bin-Nummer ersetzen, zu der er gehört. Dies kann mit der numpy-Methode digitize durchgeführt werden. In diesem Fall wissen wir genau, wie groß der Zustand ist, da er von der Anzahl der Bins abhängt, die wir für die Digitalisierung auswählen.

✅ Wir können eine lineare Interpolation verwenden, um Werte in ein endliches Intervall zu bringen (sagen wir von -20 bis 20), und dann die Zahlen durch Runden in ganze Zahlen umwandeln. Dies gibt uns ein wenig weniger Kontrolle über die Größe des Zustands, insbesondere wenn wir die genauen Bereiche der Eingabewerte nicht kennen. Zum Beispiel haben in unserem Fall 2 von 4 Werten keine oberen/unteren Grenzen für ihre Werte, was zu einer unendlichen Anzahl von Zuständen führen kann.

In unserem Beispiel werden wir den zweiten Ansatz wählen. Wie Sie später bemerken werden, nehmen diese Werte trotz undefinierter oberer/unten Grenzen selten Werte außerhalb bestimmter endlicher Intervalle an, sodass diese Zustände mit extremen Werten sehr selten sein werden.

Hier ist die Funktion, die die Beobachtung aus unserem Modell nimmt und ein Tupel aus 4 ganzzahligen Werten erzeugt: (Codeblock 6)
```
def discretize(x):
    return tuple((x/np.array([0.25, 0.25, 0.01, 0.1])).astype(np.int))
```

Lassen Sie uns auch eine andere Diskretisierungsmethode mit Bins erkunden: (Codeblock 7)

def create_bins(i,num):
    return np.arange(num+1)*(i[1]-i[0])/num+i[0]

print("Sample bins for interval (-5,5) with 10 bins\n",create_bins((-5,5),10))

ints = [(-5,5),(-2,2),(-0.5,0.5),(-2,2)] # intervals of values for each parameter
nbins = [20,20,10,10] # number of bins for each parameter
bins = [create_bins(ints[i],nbins[i]) for i in range(4)]

def discretize_bins(x):
    return tuple(np.digitize(x[i],bins[i]) for i in range(4))

Lassen Sie uns nun eine kurze Simulation durchführen und diese diskreten Umgebungswerte beobachten. Fühlen Sie sich frei, sowohl discretize and discretize_bins auszuprobieren und zu sehen, ob es einen Unterschied gibt.

✅ discretize_bins gibt die Bin-Nummer zurück, die 0-basiert ist. Daher gibt es für Werte der Eingangsvariablen um 0 die Nummer aus der Mitte des Intervalls (10) zurück. In discretize haben wir uns nicht um den Bereich der Ausgabewerte gekümmert, wodurch sie negativ werden können, sodass die Zustandswerte nicht verschoben werden und 0 0 entspricht. (Codeblock 8)
```
env.reset()

done = False
while not done:
   #env.render()
   obs, rew, done, info = env.step(env.action_space.sample())
   #print(discretize_bins(obs))
   print(discretize(obs))
env.close()
```
✅ Kommentieren Sie die Zeile, die mit env.render beginnt, aus, wenn Sie sehen möchten, wie die Umgebung ausgeführt wird. Andernfalls können Sie es im Hintergrund ausführen, was schneller ist. Wir werden diese "unsichtbare" Ausführung während unseres Q-Learning-Prozesses verwenden.

Die Struktur der Q-Tabelle

In unserer vorherigen Lektion war der Zustand ein einfaches Zahlenpaar von 0 bis 8, und daher war es praktisch, die Q-Tabelle durch einen numpy-Tensor mit einer Form von 8x8x2 darzustellen. Wenn wir die Bins-Diskretisierung verwenden, ist die Größe unseres Zustandsvektors ebenfalls bekannt, sodass wir denselben Ansatz verwenden und den Zustand durch ein Array der Form 20x20x10x10x2 darstellen können (hier ist 2 die Dimension des Aktionsraums, und die ersten Dimensionen entsprechen der Anzahl der Bins, die wir für jeden der Parameter im Beobachtungsraum ausgewählt haben).

Manchmal sind die genauen Dimensionen des Beobachtungsraums jedoch nicht bekannt. Im Fall der discretize-Funktion können wir nie sicher sein, dass unser Zustand innerhalb bestimmter Grenzen bleibt, da einige der ursprünglichen Werte nicht gebunden sind. Daher werden wir einen etwas anderen Ansatz verwenden und die Q-Tabelle durch ein Dictionary darstellen.

Verwenden Sie das Paar (Zustand, Aktion) als Schlüssel für das Dictionary, und der Wert würde dem Wert des Q-Tabelleneintrags entsprechen. (Codeblock 9)
```
Q = {}
actions = (0,1)

def qvalues(state):
    return [Q.get((state,a),0) for a in actions]
```
Hier definieren wir auch eine Funktion qvalues(), die eine Liste von Q-Tabellenwerten für einen gegebenen Zustand zurückgibt, die allen möglichen Aktionen entsprechen. Wenn der Eintrag nicht in der Q-Tabelle vorhanden ist, geben wir 0 als Standardwert zurück.

Lassen Sie uns mit Q-Learning beginnen

Jetzt sind wir bereit, Peter das Balancieren beizubringen!

Zuerst setzen wir einige Hyperparameter: (Codeblock 10)
```
# hyperparameters
alpha = 0.3
gamma = 0.9
epsilon = 0.90
```
Hier ist der alpha is the learning rate that defines to which extent we should adjust the current values of Q-Table at each step. In the previous lesson we started with 1, and then decreased alpha to lower values during training. In this example we will keep it constant just for simplicity, and you can experiment with adjusting alpha values later.

gamma is the discount factor that shows to which extent we should prioritize future reward over current reward.

epsilon is the exploration/exploitation factor that determines whether we should prefer exploration to exploitation or vice versa. In our algorithm, we will in epsilon percent of the cases select the next action according to Q-Table values, and in the remaining number of cases we will execute a random action. This will allow us to explore areas of the search space that we have never seen before.

✅ In terms of balancing - choosing random action (exploration) would act as a random punch in the wrong direction, and the pole would have to learn how to recover the balance from those "mistakes"

Improve the algorithm

We can also make two improvements to our algorithm from the previous lesson:

Calculate average cumulative reward, over a number of simulations. We will print the progress each 5000 iterations, and we will average out our cumulative reward over that period of time. It means that if we get more than 195 point - we can consider the problem solved, with even higher quality than required.
Calculate maximum average cumulative result, Qmax, and we will store the Q-Table corresponding to that result. When you run the training you will notice that sometimes the average cumulative result starts to drop, and we want to keep the values of Q-Table that correspond to the best model observed during training.

Collect all cumulative rewards at each simulation at rewards-Vektor für weitere Diagramme. (Codeblock 11)

def probs(v,eps=1e-4):
    v = v-v.min()+eps
    v = v/v.sum()
    return v

Qmax = 0
cum_rewards = []
rewards = []
for epoch in range(100000):
    obs = env.reset()
    done = False
    cum_reward=0
    # == do the simulation ==
    while not done:
        s = discretize(obs)
        if random.random()<epsilon:
            # exploitation - chose the action according to Q-Table probabilities
            v = probs(np.array(qvalues(s)))
            a = random.choices(actions,weights=v)[0]
        else:
            # exploration - randomly chose the action
            a = np.random.randint(env.action_space.n)

        obs, rew, done, info = env.step(a)
        cum_reward+=rew
        ns = discretize(obs)
        Q[(s,a)] = (1 - alpha) * Q.get((s,a),0) + alpha * (rew + gamma * max(qvalues(ns)))
    cum_rewards.append(cum_reward)
    rewards.append(cum_reward)
    # == Periodically print results and calculate average reward ==
    if epoch%5000==0:
        print(f"{epoch}: {np.average(cum_rewards)}, alpha={alpha}, epsilon={epsilon}")
        if np.average(cum_rewards) > Qmax:
            Qmax = np.average(cum_rewards)
            Qbest = Q
        cum_rewards=[]

Was Sie aus diesen Ergebnissen möglicherweise bemerken:

Nahe an unserem Ziel. Wir sind sehr nah daran, das Ziel zu erreichen, 195 kumulative Belohnungen über 100+ aufeinanderfolgende Durchläufe der Simulation zu erhalten, oder wir haben es tatsächlich erreicht! Selbst wenn wir kleinere Zahlen erhalten, wissen wir immer noch nicht, weil wir über 5000 Durchläufe im Durchschnitt nehmen, und nur 100 Durchläufe sind im formalen Kriterium erforderlich.
Belohnung beginnt zu sinken. Manchmal beginnt die Belohnung zu sinken, was bedeutet, dass wir bereits erlernte Werte in der Q-Tabelle durch solche ersetzen können, die die Situation verschlechtern.

Diese Beobachtung ist klarer sichtbar, wenn wir den Trainingsfortschritt darstellen.

Darstellung des Trainingsfortschritts

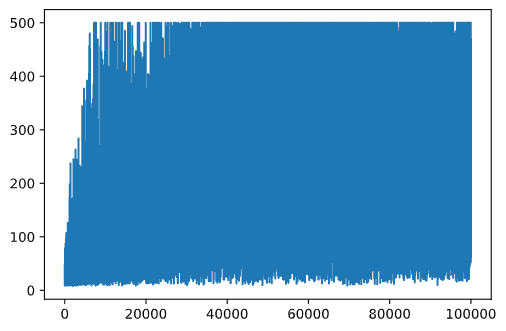
Während des Trainings haben wir den kumulierten Belohnungswert bei jeder der Iterationen in den rewards-Vektor gesammelt. Hier ist, wie es aussieht, wenn wir es gegen die Iterationsnummer darstellen:

plt.plot(rewards)

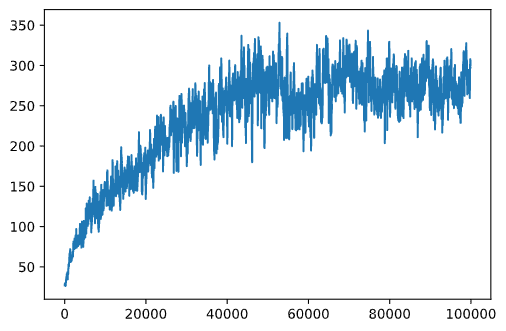
Aus diesem Diagramm ist nichts zu erkennen, da aufgrund der Natur des stochastischen Trainingsprozesses die Länge der Trainingssitzungen stark variiert. Um mehr Sinn aus diesem Diagramm zu ziehen, können wir den laufenden Durchschnitt über eine Reihe von Experimenten berechnen, sagen wir 100. Dies kann bequem mit np.convolve durchgeführt werden: (Codeblock 12)

def running_average(x,window):
    return np.convolve(x,np.ones(window)/window,mode='valid')

plt.plot(running_average(rewards,100))

Variieren der Hyperparameter

Um das Lernen stabiler zu machen, ist es sinnvoll, einige unserer Hyperparameter während des Trainings anzupassen. Insbesondere:

Für die Lernrate, alpha, we may start with values close to 1, and then keep decreasing the parameter. With time, we will be getting good probability values in the Q-Table, and thus we should be adjusting them slightly, and not overwriting completely with new values.
Increase epsilon. We may want to increase the epsilon slowly, in order to explore less and exploit more. It probably makes sense to start with lower value of epsilon, und sich bis fast 1 bewegen.

Aufgabe 1: Spielen Sie mit den Hyperparameterwerten und sehen Sie, ob Sie eine höhere kumulierte Belohnung erzielen können. Erreichen Sie über 195?

Aufgabe 2: Um das Problem formal zu lösen, müssen Sie einen durchschnittlichen Belohnungswert von 195 über 100 aufeinanderfolgende Durchläufe erzielen. Messen Sie das während des Trainings und stellen Sie sicher, dass Sie das Problem formal gelöst haben!

Die Ergebnisse in Aktion sehen

Es wäre interessant zu sehen, wie sich das trainierte Modell verhält. Lassen Sie uns die Simulation ausführen und die gleiche Aktionsauswahlstrategie wie während des Trainings befolgen, indem wir gemäß der Wahrscheinlichkeitsverteilung in der Q-Tabelle sampeln: (Codeblock 13)

obs = env.reset()
done = False
while not done:
   s = discretize(obs)
   env.render()
   v = probs(np.array(qvalues(s)))
   a = random.choices(actions,weights=v)[0]
   obs,_,done,_ = env.step(a)
env.close()

Sie sollten etwas Ähnliches sehen:

🚀Herausforderung

Aufgabe 3: Hier haben wir die endgültige Kopie der Q-Tabelle verwendet, die möglicherweise nicht die beste ist. Denken Sie daran, dass wir die leistungsstärkste Q-Tabelle in Qbest variable! Try the same example with the best-performing Q-Table by copying Qbest over to Q and see if you notice the difference.

Task 4: Here we were not selecting the best action on each step, but rather sampling with corresponding probability distribution. Would it make more sense to always select the best action, with the highest Q-Table value? This can be done by using np.argmax gespeichert haben, um die Aktionsnummer zu finden, die dem höchsten Q-Tabellenwert entspricht. Implementieren Sie diese Strategie und sehen Sie, ob sie das Balancieren verbessert.

Nachlesungsquiz

Aufgabe

Trainiere ein Mountain Car

Fazit

Wir haben jetzt gelernt, wie man Agenten trainiert, um gute Ergebnisse zu erzielen, indem wir ihnen lediglich eine Belohnungsfunktion bereitstellen, die den gewünschten Zustand des Spiels definiert, und indem wir ihnen die Möglichkeit geben, den Suchraum intelligent zu erkunden. Wir haben den Q-Learning-Algorithmus erfolgreich in Fällen diskreter und kontinuierlicher Umgebungen angewendet, jedoch mit diskreten Aktionen.

Es ist auch wichtig, Situationen zu studieren, in denen der Aktionszustand ebenfalls kontinuierlich ist und wenn der Beobachtungsraum viel komplexer ist, wie z.B. das Bild vom Atari-Spielbildschirm. In diesen Problemen müssen wir oft leistungsfähigere Techniken des maschinellen Lernens, wie neuronale Netzwerke, einsetzen, um gute Ergebnisse zu erzielen. Diese fortgeschrittenen Themen sind Gegenstand unseres kommenden, fortgeschrittenen KI-Kurses.

Haftungsausschluss:
Dieses Dokument wurde mithilfe von KI-gestützten Übersetzungsdiensten übersetzt. Obwohl wir uns um Genauigkeit bemühen, beachten Sie bitte, dass automatisierte Übersetzungen Fehler oder Ungenauigkeiten enthalten können. Das Originaldokument in seiner Ursprungssprache sollte als maßgebliche Quelle betrachtet werden. Für wichtige Informationen wird eine professionelle menschliche Übersetzung empfohlen. Wir übernehmen keine Haftung für Missverständnisse oder Fehlinterpretationen, die aus der Verwendung dieser Übersetzung entstehen.