|
|
8 months ago | |
|---|---|---|
| .. | ||
| solution | 8 months ago | |
| README.md | 8 months ago | |
| assignment.md | 8 months ago | |
README.md
Prasyarat
Dalam pelajaran ini, kita akan menggunakan pustaka yang disebut OpenAI Gym untuk mensimulasikan berbagai lingkungan. Anda dapat menjalankan kode pelajaran ini secara lokal (misalnya dari Visual Studio Code), di mana simulasi akan terbuka di jendela baru. Saat menjalankan kode secara online, Anda mungkin perlu melakukan beberapa penyesuaian pada kode, seperti yang dijelaskan di sini.
OpenAI Gym
Dalam pelajaran sebelumnya, aturan permainan dan keadaan diberikan oleh kelas Board yang kita definisikan sendiri. Di sini kita akan menggunakan lingkungan simulasi khusus, yang akan mensimulasikan fisika di balik keseimbangan tiang. Salah satu lingkungan simulasi paling populer untuk melatih algoritma pembelajaran penguatan disebut Gym, yang dikelola oleh OpenAI. Dengan menggunakan gym ini kita dapat membuat berbagai lingkungan dari simulasi cartpole hingga permainan Atari.
Catatan: Anda dapat melihat lingkungan lain yang tersedia dari OpenAI Gym di sini.
Pertama, mari kita instal gym dan impor pustaka yang diperlukan (kode blok 1):
import sys
!{sys.executable} -m pip install gym
import gym
import matplotlib.pyplot as plt
import numpy as np
import random
Latihan - inisialisasi lingkungan cartpole
Untuk bekerja dengan masalah keseimbangan cartpole, kita perlu menginisialisasi lingkungan yang sesuai. Setiap lingkungan terkait dengan:
-
Observation space yang mendefinisikan struktur informasi yang kita terima dari lingkungan. Untuk masalah cartpole, kita menerima posisi tiang, kecepatan, dan beberapa nilai lainnya.
-
Action space yang mendefinisikan tindakan yang mungkin dilakukan. Dalam kasus kita, action space bersifat diskrit, dan terdiri dari dua tindakan - kiri dan kanan. (kode blok 2)
-
Untuk menginisialisasi, ketik kode berikut:
env = gym.make("CartPole-v1") print(env.action_space) print(env.observation_space) print(env.action_space.sample())
Untuk melihat bagaimana lingkungan bekerja, mari kita jalankan simulasi singkat selama 100 langkah. Pada setiap langkah, kita memberikan salah satu tindakan yang akan diambil - dalam simulasi ini kita hanya memilih tindakan secara acak dari action_space.
-
Jalankan kode di bawah ini dan lihat hasilnya.
✅ Ingat bahwa lebih disukai untuk menjalankan kode ini pada instalasi Python lokal! (kode blok 3)
env.reset() for i in range(100): env.render() env.step(env.action_space.sample()) env.close()Anda harus melihat sesuatu yang mirip dengan gambar ini:
-
Selama simulasi, kita perlu mendapatkan pengamatan untuk memutuskan bagaimana bertindak. Faktanya, fungsi langkah mengembalikan pengamatan saat ini, fungsi reward, dan flag selesai yang menunjukkan apakah masuk akal untuk melanjutkan simulasi atau tidak: (kode blok 4)
env.reset() done = False while not done: env.render() obs, rew, done, info = env.step(env.action_space.sample()) print(f"{obs} -> {rew}") env.close()Anda akan melihat sesuatu seperti ini di output notebook:
[ 0.03403272 -0.24301182 0.02669811 0.2895829 ] -> 1.0 [ 0.02917248 -0.04828055 0.03248977 0.00543839] -> 1.0 [ 0.02820687 0.14636075 0.03259854 -0.27681916] -> 1.0 [ 0.03113408 0.34100283 0.02706215 -0.55904489] -> 1.0 [ 0.03795414 0.53573468 0.01588125 -0.84308041] -> 1.0 ... [ 0.17299878 0.15868546 -0.20754175 -0.55975453] -> 1.0 [ 0.17617249 0.35602306 -0.21873684 -0.90998894] -> 1.0Vektor pengamatan yang dikembalikan pada setiap langkah simulasi berisi nilai-nilai berikut:
- Posisi kereta
- Kecepatan kereta
- Sudut tiang
- Laju rotasi tiang
-
Dapatkan nilai min dan max dari angka-angka tersebut: (kode blok 5)
print(env.observation_space.low) print(env.observation_space.high)Anda mungkin juga memperhatikan bahwa nilai reward pada setiap langkah simulasi selalu 1. Ini karena tujuan kita adalah bertahan selama mungkin, yaitu menjaga tiang tetap dalam posisi vertikal selama mungkin.
✅ Faktanya, simulasi CartPole dianggap berhasil jika kita berhasil mendapatkan reward rata-rata 195 selama 100 percobaan berturut-turut.
Diskritisasi State
Dalam Q-Learning, kita perlu membangun Q-Table yang mendefinisikan apa yang harus dilakukan pada setiap state. Untuk dapat melakukan ini, kita memerlukan state yang diskrit, lebih tepatnya, harus mengandung sejumlah nilai diskrit yang terbatas. Oleh karena itu, kita perlu mendiskritkan pengamatan kita, memetakan mereka ke dalam satu set state yang terbatas.
Ada beberapa cara kita bisa melakukannya:
- Membagi menjadi bin. Jika kita mengetahui interval dari nilai tertentu, kita bisa membagi interval ini menjadi beberapa bin, dan kemudian mengganti nilai dengan nomor bin yang dimasukinya. Ini bisa dilakukan menggunakan metode numpy
digitize. Dalam kasus ini, kita akan mengetahui ukuran state dengan tepat, karena akan tergantung pada jumlah bin yang kita pilih untuk digitalisasi.
✅ Kita bisa menggunakan interpolasi linier untuk membawa nilai ke beberapa interval terbatas (misalnya, dari -20 hingga 20), dan kemudian mengonversi angka menjadi bilangan bulat dengan membulatkannya. Ini memberi kita sedikit kontrol lebih pada ukuran state, terutama jika kita tidak mengetahui rentang nilai input yang tepat. Misalnya, dalam kasus kita, 2 dari 4 nilai tidak memiliki batas atas/bawah pada nilai mereka, yang dapat mengakibatkan jumlah state yang tak terbatas.
Dalam contoh kita, kita akan menggunakan pendekatan kedua. Seperti yang mungkin Anda perhatikan nanti, meskipun batas atas/bawah tidak ditentukan, nilai-nilai tersebut jarang mengambil nilai di luar interval terbatas tertentu, sehingga state dengan nilai ekstrem akan sangat jarang.
-
Berikut adalah fungsi yang akan mengambil pengamatan dari model kita dan menghasilkan tuple dari 4 nilai integer: (kode blok 6)
def discretize(x): return tuple((x/np.array([0.25, 0.25, 0.01, 0.1])).astype(np.int)) -
Mari kita juga eksplorasi metode diskritisasi lain menggunakan bin: (kode blok 7)
def create_bins(i,num): return np.arange(num+1)*(i[1]-i[0])/num+i[0] print("Sample bins for interval (-5,5) with 10 bins\n",create_bins((-5,5),10)) ints = [(-5,5),(-2,2),(-0.5,0.5),(-2,2)] # intervals of values for each parameter nbins = [20,20,10,10] # number of bins for each parameter bins = [create_bins(ints[i],nbins[i]) for i in range(4)] def discretize_bins(x): return tuple(np.digitize(x[i],bins[i]) for i in range(4)) -
Sekarang mari kita jalankan simulasi singkat dan amati nilai lingkungan diskrit tersebut. Silakan coba keduanya
discretizeanddiscretize_binsdan lihat apakah ada perbedaan.✅ discretize_bins mengembalikan nomor bin, yang berbasis 0. Jadi untuk nilai variabel input sekitar 0, ia mengembalikan nomor dari tengah interval (10). Dalam discretize, kita tidak peduli dengan rentang nilai output, memungkinkan mereka menjadi negatif, sehingga nilai state tidak bergeser, dan 0 sesuai dengan 0. (kode blok 8)
env.reset() done = False while not done: #env.render() obs, rew, done, info = env.step(env.action_space.sample()) #print(discretize_bins(obs)) print(discretize(obs)) env.close()✅ Hapus komentar pada baris yang dimulai dengan env.render jika Anda ingin melihat bagaimana lingkungan dieksekusi. Jika tidak, Anda dapat mengeksekusinya di latar belakang, yang lebih cepat. Kita akan menggunakan eksekusi "tak terlihat" ini selama proses Q-Learning kita.
Struktur Q-Table
Dalam pelajaran sebelumnya, state adalah pasangan angka sederhana dari 0 hingga 8, dan dengan demikian nyaman untuk mewakili Q-Table dengan tensor numpy dengan bentuk 8x8x2. Jika kita menggunakan diskritisasi bin, ukuran vektor state kita juga diketahui, sehingga kita dapat menggunakan pendekatan yang sama dan mewakili state dengan array berbentuk 20x20x10x10x2 (di sini 2 adalah dimensi dari action space, dan dimensi pertama sesuai dengan jumlah bin yang kita pilih untuk digunakan untuk setiap parameter dalam observation space).
Namun, terkadang dimensi tepat dari observation space tidak diketahui. Dalam kasus fungsi discretize, kita mungkin tidak pernah yakin bahwa state kita tetap dalam batas tertentu, karena beberapa nilai asli tidak dibatasi. Oleh karena itu, kita akan menggunakan pendekatan yang sedikit berbeda dan mewakili Q-Table dengan kamus.
-
Gunakan pasangan (state,action) sebagai kunci kamus, dan nilai akan sesuai dengan nilai entri Q-Table. (kode blok 9)
Q = {} actions = (0,1) def qvalues(state): return [Q.get((state,a),0) for a in actions]Di sini kita juga mendefinisikan fungsi
qvalues(), yang mengembalikan daftar nilai Q-Table untuk state tertentu yang sesuai dengan semua tindakan yang mungkin. Jika entri tidak ada dalam Q-Table, kita akan mengembalikan 0 sebagai default.
Mari Mulai Q-Learning
Sekarang kita siap mengajarkan Peter untuk menjaga keseimbangan!
-
Pertama, mari kita atur beberapa hyperparameter: (kode blok 10)
# hyperparameters alpha = 0.3 gamma = 0.9 epsilon = 0.90Di sini,
alphais the learning rate that defines to which extent we should adjust the current values of Q-Table at each step. In the previous lesson we started with 1, and then decreasedalphato lower values during training. In this example we will keep it constant just for simplicity, and you can experiment with adjustingalphavalues later.gammais the discount factor that shows to which extent we should prioritize future reward over current reward.epsilonis the exploration/exploitation factor that determines whether we should prefer exploration to exploitation or vice versa. In our algorithm, we will inepsilonpercent of the cases select the next action according to Q-Table values, and in the remaining number of cases we will execute a random action. This will allow us to explore areas of the search space that we have never seen before.✅ In terms of balancing - choosing random action (exploration) would act as a random punch in the wrong direction, and the pole would have to learn how to recover the balance from those "mistakes"
Improve the algorithm
We can also make two improvements to our algorithm from the previous lesson:
-
Calculate average cumulative reward, over a number of simulations. We will print the progress each 5000 iterations, and we will average out our cumulative reward over that period of time. It means that if we get more than 195 point - we can consider the problem solved, with even higher quality than required.
-
Calculate maximum average cumulative result,
Qmax, and we will store the Q-Table corresponding to that result. When you run the training you will notice that sometimes the average cumulative result starts to drop, and we want to keep the values of Q-Table that correspond to the best model observed during training.
-
Collect all cumulative rewards at each simulation at
rewardsvektor untuk plot lebih lanjut. (kode blok 11)def probs(v,eps=1e-4): v = v-v.min()+eps v = v/v.sum() return v Qmax = 0 cum_rewards = [] rewards = [] for epoch in range(100000): obs = env.reset() done = False cum_reward=0 # == do the simulation == while not done: s = discretize(obs) if random.random()<epsilon: # exploitation - chose the action according to Q-Table probabilities v = probs(np.array(qvalues(s))) a = random.choices(actions,weights=v)[0] else: # exploration - randomly chose the action a = np.random.randint(env.action_space.n) obs, rew, done, info = env.step(a) cum_reward+=rew ns = discretize(obs) Q[(s,a)] = (1 - alpha) * Q.get((s,a),0) + alpha * (rew + gamma * max(qvalues(ns))) cum_rewards.append(cum_reward) rewards.append(cum_reward) # == Periodically print results and calculate average reward == if epoch%5000==0: print(f"{epoch}: {np.average(cum_rewards)}, alpha={alpha}, epsilon={epsilon}") if np.average(cum_rewards) > Qmax: Qmax = np.average(cum_rewards) Qbest = Q cum_rewards=[]
Apa yang mungkin Anda perhatikan dari hasil tersebut:
-
Dekat dengan tujuan kita. Kita sangat dekat mencapai tujuan mendapatkan 195 reward kumulatif selama 100+ percobaan berturut-turut dari simulasi, atau kita mungkin telah mencapainya! Bahkan jika kita mendapatkan angka yang lebih kecil, kita masih tidak tahu, karena kita rata-rata lebih dari 5000 percobaan, dan hanya 100 percobaan yang diperlukan dalam kriteria formal.
-
Reward mulai menurun. Kadang-kadang reward mulai menurun, yang berarti kita dapat "menghancurkan" nilai yang sudah dipelajari dalam Q-Table dengan yang membuat situasi lebih buruk.
Pengamatan ini lebih jelas terlihat jika kita plot kemajuan pelatihan.
Plotting Kemajuan Pelatihan
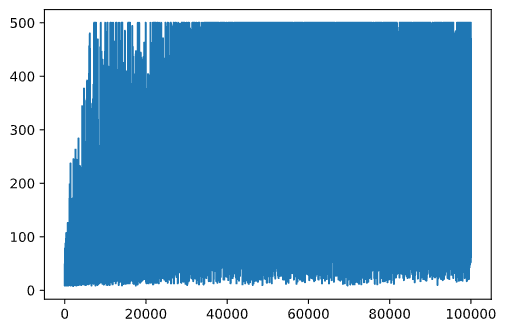
Selama pelatihan, kita telah mengumpulkan nilai reward kumulatif pada setiap iterasi ke dalam vektor rewards. Berikut adalah tampilannya saat kita plot terhadap nomor iterasi:
plt.plot(rewards)
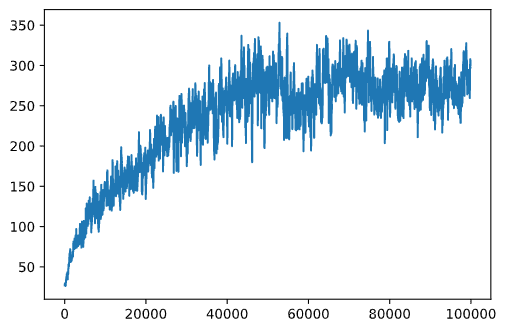
Dari grafik ini, tidak mungkin untuk mengatakan apa pun, karena sifat dari proses pelatihan stokastik panjang sesi pelatihan sangat bervariasi. Untuk lebih memahami grafik ini, kita dapat menghitung rata-rata berjalan selama serangkaian eksperimen, katakanlah 100. Ini dapat dilakukan dengan mudah menggunakan np.convolve: (kode blok 12)
def running_average(x,window):
return np.convolve(x,np.ones(window)/window,mode='valid')
plt.plot(running_average(rewards,100))
Memvariasikan hyperparameter
Untuk membuat pembelajaran lebih stabil, masuk akal untuk menyesuaikan beberapa hyperparameter kita selama pelatihan. Secara khusus:
-
Untuk learning rate,
alpha, we may start with values close to 1, and then keep decreasing the parameter. With time, we will be getting good probability values in the Q-Table, and thus we should be adjusting them slightly, and not overwriting completely with new values. -
Increase epsilon. We may want to increase the
epsilonslowly, in order to explore less and exploit more. It probably makes sense to start with lower value ofepsilon, dan naik hingga hampir 1.
Tugas 1: Bermainlah dengan nilai hyperparameter dan lihat apakah Anda dapat mencapai reward kumulatif yang lebih tinggi. Apakah Anda mendapatkan di atas 195?
Tugas 2: Untuk secara formal menyelesaikan masalah, Anda perlu mendapatkan 195 reward rata-rata di 100 percobaan berturut-turut. Ukur itu selama pelatihan dan pastikan bahwa Anda telah menyelesaikan masalah secara formal!
Melihat hasilnya dalam aksi
Akan menarik untuk benar-benar melihat bagaimana model yang dilatih berperilaku. Mari kita jalankan simulasi dan mengikuti strategi pemilihan tindakan yang sama seperti selama pelatihan, sampling sesuai dengan distribusi probabilitas di Q-Table: (kode blok 13)
obs = env.reset()
done = False
while not done:
s = discretize(obs)
env.render()
v = probs(np.array(qvalues(s)))
a = random.choices(actions,weights=v)[0]
obs,_,done,_ = env.step(a)
env.close()
Anda harus melihat sesuatu seperti ini:
🚀Tantangan
Tugas 3: Di sini, kita menggunakan salinan akhir dari Q-Table, yang mungkin bukan yang terbaik. Ingat bahwa kita telah menyimpan Q-Table dengan performa terbaik ke dalam
Qbestvariable! Try the same example with the best-performing Q-Table by copyingQbestover toQand see if you notice the difference.
Task 4: Here we were not selecting the best action on each step, but rather sampling with corresponding probability distribution. Would it make more sense to always select the best action, with the highest Q-Table value? This can be done by using
np.argmaxfungsi untuk menemukan nomor tindakan yang sesuai dengan nilai Q-Table tertinggi. Implementasikan strategi ini dan lihat apakah itu meningkatkan keseimbangan.
Kuis setelah kuliah
Tugas
Kesimpulan
Kita sekarang telah belajar bagaimana melatih agen untuk mencapai hasil yang baik hanya dengan memberikan mereka fungsi reward yang mendefinisikan keadaan permainan yang diinginkan, dan dengan memberi mereka kesempatan untuk menjelajahi ruang pencarian secara cerdas. Kita telah berhasil menerapkan algoritma Q-Learning dalam kasus lingkungan diskrit dan kontinu, tetapi dengan tindakan diskrit.
Penting juga untuk mempelajari situasi di mana state tindakan juga kontinu, dan ketika observation space jauh lebih kompleks, seperti gambar dari layar permainan Atari. Dalam masalah tersebut, kita sering perlu menggunakan teknik pembelajaran mesin yang lebih kuat, seperti jaringan saraf, untuk mencapai hasil yang baik. Topik yang lebih maju ini adalah subjek dari kursus AI tingkat lanjut kita yang akan datang.
Penafian: Dokumen ini telah diterjemahkan menggunakan perkhidmatan terjemahan AI berasaskan mesin. Walaupun kami berusaha untuk ketepatan, sila ambil perhatian bahawa terjemahan automatik mungkin mengandungi kesilapan atau ketidaktepatan. Dokumen asal dalam bahasa asalnya harus dianggap sebagai sumber yang berwibawa. Untuk maklumat kritikal, terjemahan manusia profesional adalah disyorkan. Kami tidak bertanggungjawab atas sebarang salah faham atau salah tafsir yang timbul daripada penggunaan terjemahan ini.