History

Pikachú 9e189e28e2 updated translations for ko, es, it, ja, sw, hi, tr and zh using co-op translator		8 months ago
..
solution	updated translations for ko, es, it, ja, sw, hi, tr and zh using co-op translator	8 months ago
README.md	updated translations for ko, es, it, ja, sw, hi, tr and zh using co-op translator	8 months ago
assignment.md	updated translations for ko, es, it, ja, sw, hi, tr and zh using co-op translator	8 months ago

README.md

CartPole स्केटिंग

पिछले पाठ में हमने जिस समस्या को हल किया था, वह एक खिलौना समस्या की तरह लग सकती है, जो वास्तव में वास्तविक जीवन परिदृश्यों के लिए लागू नहीं होती है। ऐसा नहीं है, क्योंकि कई वास्तविक दुनिया की समस्याएं भी इस परिदृश्य को साझा करती हैं - जिसमें शतरंज या गो खेलना भी शामिल है। वे समान हैं, क्योंकि हमारे पास दिए गए नियमों के साथ एक बोर्ड भी है और एक डिस्क्रीट स्टेट।

प्री-लेक्चर क्विज़

परिचय

इस पाठ में हम Q-लर्निंग के समान सिद्धांतों को एक समस्या पर लागू करेंगे जिसमें कंटीन्यूअस स्टेट होता है, यानी एक स्टेट जो एक या अधिक वास्तविक संख्याओं द्वारा दी जाती है। हम निम्नलिखित समस्या से निपटेंगे:

समस्या: अगर पीटर को भेड़िये से बचना है, तो उसे तेजी से चलने में सक्षम होना चाहिए। हम देखेंगे कि पीटर कैसे स्केट करना सीख सकता है, विशेष रूप से संतुलन बनाए रखना, Q-लर्निंग का उपयोग करके।

पीटर और उसके दोस्त भेड़िये से बचने के लिए रचनात्मक हो जाते हैं! चित्र Jen Looper द्वारा

हम संतुलन के रूप में ज्ञात एक सरलीकृत संस्करण का उपयोग करेंगे जिसे CartPole समस्या कहा जाता है। CartPole की दुनिया में, हमारे पास एक क्षैतिज स्लाइडर है जो बाएं या दाएं चल सकता है, और लक्ष्य स्लाइडर के ऊपर एक लंबवत पोल को संतुलित करना है।

आवश्यकताएँ

इस पाठ में, हम OpenAI Gym नामक एक लाइब्रेरी का उपयोग करेंगे विभिन्न एनवायरनमेंट्स का अनुकरण करने के लिए। आप इस पाठ के कोड को स्थानीय रूप से (जैसे कि Visual Studio Code से) चला सकते हैं, इस स्थिति में अनुकरण एक नई विंडो में खुलेगा। ऑनलाइन कोड चलाते समय, आपको कोड में कुछ समायोजन करने की आवश्यकता हो सकती है, जैसा कि यहाँ वर्णित है।

OpenAI Gym

पिछले पाठ में, खेल के नियम और स्टेट Board क्लास द्वारा दिए गए थे जिसे हमने स्वयं परिभाषित किया था। यहाँ हम एक विशेष सिमुलेशन एनवायरनमेंट का उपयोग करेंगे, जो संतुलन पोल के पीछे के भौतिकी का अनुकरण करेगा। सबसे लोकप्रिय सिमुलेशन एनवायरनमेंट्स में से एक जिसे रिइनफोर्समेंट लर्निंग एल्गोरिदम के प्रशिक्षण के लिए उपयोग किया जाता है, उसे Gym कहा जाता है, जो OpenAI द्वारा बनाए रखा जाता है। इस जिम का उपयोग करके हम कार्टपोल सिमुलेशन से लेकर अटारी गेम्स तक विभिन्न एनवायरनमेंट्स बना सकते हैं।

नोट: आप OpenAI Gym से उपलब्ध अन्य एनवायरनमेंट्स को यहाँ देख सकते हैं।

पहले, जिम को इंस्टॉल करें और आवश्यक लाइब्रेरीज़ को इम्पोर्ट करें (कोड ब्लॉक 1):

import sys
!{sys.executable} -m pip install gym 

import gym
import matplotlib.pyplot as plt
import numpy as np
import random

व्यायाम - एक कार्टपोल एनवायरनमेंट को प्रारंभ करें

कार्टपोल संतुलन समस्या के साथ काम करने के लिए, हमें संबंधित एनवायरनमेंट को प्रारंभ करना होगा। प्रत्येक एनवायरनमेंट के साथ एक:

ऑब्जर्वेशन स्पेस जुड़ा होता है जो उस जानकारी की संरचना को परिभाषित करता है जो हमें एनवायरनमेंट से प्राप्त होती है। कार्टपोल समस्या के लिए, हमें पोल की स्थिति, वेग और कुछ अन्य मान प्राप्त होते हैं।
एक्शन स्पेस जो संभावित कार्यों को परिभाषित करता है। हमारे मामले में एक्शन स्पेस डिस्क्रीट है, और इसमें दो कार्य शामिल हैं - बाएं और दाएं। (कोड ब्लॉक 2)

प्रारंभ करने के लिए, निम्नलिखित कोड टाइप करें:

env = gym.make("CartPole-v1")
print(env.action_space)
print(env.observation_space)
print(env.action_space.sample())

एनवायरनमेंट कैसे काम करता है यह देखने के लिए, चलिए 100 चरणों के लिए एक छोटी सिमुलेशन चलाते हैं। प्रत्येक चरण में, हम एक कार्य प्रदान करते हैं - इस सिमुलेशन में हम बस action_space से एक कार्य को यादृच्छिक रूप से चुनते हैं।

नीचे दिए गए कोड को चलाएं और देखें कि इसका परिणाम क्या है।

✅ याद रखें कि इस कोड को स्थानीय Python इंस्टॉलेशन पर चलाना बेहतर है! (कोड ब्लॉक 3)
```
env.reset()

for i in range(100):
   env.render()
   env.step(env.action_space.sample())
env.close()
```
आपको इस छवि के समान कुछ देखना चाहिए:
सिमुलेशन के दौरान, हमें यह तय करने के लिए ऑब्जर्वेशन प्राप्त करने की आवश्यकता होती है कि कैसे कार्य करना है। वास्तव में, स्टेप फ़ंक्शन वर्तमान ऑब्जर्वेशन, एक रिवार्ड फ़ंक्शन और डन फ्लैग लौटाता है जो इंगित करता है कि सिमुलेशन जारी रखने का कोई मतलब है या नहीं: (कोड ब्लॉक 4)
```
env.reset()

done = False
while not done:
   env.render()
   obs, rew, done, info = env.step(env.action_space.sample())
   print(f"{obs} -> {rew}")
env.close()
```
आपको नोटबुक आउटपुट में कुछ ऐसा ही देखना चाहिए:
```
[ 0.03403272 -0.24301182  0.02669811  0.2895829 ] -> 1.0
[ 0.02917248 -0.04828055  0.03248977  0.00543839] -> 1.0
[ 0.02820687  0.14636075  0.03259854 -0.27681916] -> 1.0
[ 0.03113408  0.34100283  0.02706215 -0.55904489] -> 1.0
[ 0.03795414  0.53573468  0.01588125 -0.84308041] -> 1.0
...
[ 0.17299878  0.15868546 -0.20754175 -0.55975453] -> 1.0
[ 0.17617249  0.35602306 -0.21873684 -0.90998894] -> 1.0
```
सिमुलेशन के प्रत्येक चरण में लौटाए गए ऑब्जर्वेशन वेक्टर में निम्नलिखित मान शामिल होते हैं:
- कार्ट की स्थिति
- कार्ट की वेग
- पोल का कोण
- पोल का रोटेशन दर
उन संख्याओं का न्यूनतम और अधिकतम मान प्राप्त करें: (कोड ब्लॉक 5)
```
print(env.observation_space.low)
print(env.observation_space.high)
```
आप यह भी देख सकते हैं कि प्रत्येक सिमुलेशन चरण पर रिवार्ड मान हमेशा 1 होता है। इसका कारण यह है कि हमारा लक्ष्य जितना संभव हो सके जीवित रहना है, यानी पोल को यथासंभव लंबवत स्थिति में रखना है।

✅ वास्तव में, यदि हम 100 लगातार परीक्षणों में 195 का औसत रिवार्ड प्राप्त करने में सफल होते हैं तो CartPole सिमुलेशन को हल किया जाता है।

स्टेट का डिस्क्रीटाइजेशन

Q-लर्निंग में, हमें Q-टेबल बनाना होता है जो परिभाषित करता है कि प्रत्येक स्टेट पर क्या करना है। ऐसा करने में सक्षम होने के लिए, हमें स्टेट को डिस्क्रीट बनाना होगा, अधिक सटीक रूप से, इसमें सीमित संख्या में डिस्क्रीट मान शामिल होने चाहिए। इस प्रकार, हमें किसी प्रकार से अपने ऑब्जर्वेशन को डिस्क्रीटाइज करना होगा, उन्हें सीमित स्टेट सेट में मैप करना होगा।

हम इसे करने के कुछ तरीके हैं:

बिन्स में विभाजित करें। यदि हमें किसी मान का अंतराल पता है, तो हम इस अंतराल को कई बिन्स में विभाजित कर सकते हैं, और फिर उस मान को बिन नंबर से बदल सकते हैं जिसमें यह आता है। यह numpy digitize विधि का उपयोग करके किया जा सकता है। इस मामले में, हम स्टेट आकार को ठीक से जानेंगे, क्योंकि यह उन बिन्स की संख्या पर निर्भर करेगा जिन्हें हम डिजिटलीकरण के लिए चुनते हैं।

✅ हम मूल्यों को किसी सीमित अंतराल (कहें, -20 से 20 तक) में लाने के लिए रैखिक इंटरपोलेशन का उपयोग कर सकते हैं, और फिर उन्हें गोल करके पूर्णांकों में बदल सकते हैं। इससे हमें स्टेट के आकार पर थोड़ा कम नियंत्रण मिलता है, विशेष रूप से यदि हमें इनपुट मूल्यों की सटीक रेंज नहीं पता है। उदाहरण के लिए, हमारे मामले में 4 में से 2 मानों की कोई ऊपरी/निचली सीमा नहीं है, जिससे असीमित संख्या में स्टेट हो सकते हैं।

हमारे उदाहरण में, हम दूसरे दृष्टिकोण के साथ जाएंगे। जैसा कि आप बाद में देख सकते हैं, अपरिभाषित ऊपरी/निचली सीमाओं के बावजूद, वे मान शायद ही कभी कुछ सीमित अंतरालों के बाहर मान लेते हैं, इस प्रकार उन स्टेट्स के साथ चरम मान बहुत दुर्लभ होंगे।

यहाँ वह फ़ंक्शन है जो हमारे मॉडल से ऑब्जर्वेशन लेगा और 4 पूर्णांक मानों का एक ट्यूपल उत्पन्न करेगा: (कोड ब्लॉक 6)
```
def discretize(x):
    return tuple((x/np.array([0.25, 0.25, 0.01, 0.1])).astype(np.int))
```

चलिए बिन्स का उपयोग करके एक और डिस्क्रीटाइजेशन विधि का भी अन्वेषण करते हैं: (कोड ब्लॉक 7)

def create_bins(i,num):
    return np.arange(num+1)*(i[1]-i[0])/num+i[0]

print("Sample bins for interval (-5,5) with 10 bins\n",create_bins((-5,5),10))

ints = [(-5,5),(-2,2),(-0.5,0.5),(-2,2)] # intervals of values for each parameter
nbins = [20,20,10,10] # number of bins for each parameter
bins = [create_bins(ints[i],nbins[i]) for i in range(4)]

def discretize_bins(x):
    return tuple(np.digitize(x[i],bins[i]) for i in range(4))

अब चलिए एक छोटी सिमुलेशन चलाते हैं और उन डिस्क्रीट एनवायरनमेंट मूल्यों का अवलोकन करते हैं। discretize and discretize_bins दोनों का उपयोग करने का प्रयास करें और देखें कि क्या कोई अंतर है।

✅ discretize_bins बिन नंबर लौटाता है, जो 0-आधारित होता है। इस प्रकार इनपुट वेरिएबल के चारों ओर 0 के मानों के लिए यह अंतराल के मध्य से संख्या लौटाता है (10)। डिस्क्रीटाइज में, हमने आउटपुट मानों की रेंज की परवाह नहीं की, उन्हें नकारात्मक होने की अनुमति दी, इस प्रकार स्टेट मान स्थानांतरित नहीं होते, और 0 का मतलब 0 होता है। (कोड ब्लॉक 8)
```
env.reset()

done = False
while not done:
   #env.render()
   obs, rew, done, info = env.step(env.action_space.sample())
   #print(discretize_bins(obs))
   print(discretize(obs))
env.close()
```
✅ यदि आप देखना चाहते हैं कि एनवायरनमेंट कैसे निष्पादित होता है तो env.render से शुरू होने वाली पंक्ति को अनकमेंट करें। अन्यथा आप इसे पृष्ठभूमि में निष्पादित कर सकते हैं, जो तेज है। हम इस "अदृश्य" निष्पादन का उपयोग Q-लर्निंग प्रक्रिया के दौरान करेंगे।

Q-टेबल संरचना

हमारे पिछले पाठ में, स्टेट एक साधारण संख्या जोड़ी थी 0 से 8 तक, और इस प्रकार Q-टेबल को 8x8x2 आकार के numpy टेंसर द्वारा प्रस्तुत करना सुविधाजनक था। यदि हम बिन्स डिस्क्रीटाइजेशन का उपयोग करते हैं, तो हमारे स्टेट वेक्टर का आकार भी ज्ञात होता है, इसलिए हम उसी दृष्टिकोण का उपयोग कर सकते हैं और स्टेट को 20x20x10x10x2 आकार के एक सरणी द्वारा प्रस्तुत कर सकते हैं (यहाँ 2 एक्शन स्पेस का आयाम है, और पहले आयाम ऑब्जर्वेशन स्पेस में प्रत्येक पैरामीटर के लिए उपयोग किए गए बिन्स की संख्या से मेल खाते हैं)।

हालांकि, कभी-कभी ऑब्जर्वेशन स्पेस के सटीक आयाम ज्ञात नहीं होते हैं। discretize फ़ंक्शन के मामले में, हम कभी भी यह सुनिश्चित नहीं कर सकते कि हमारा स्टेट निश्चित सीमाओं के भीतर रहता है, क्योंकि कुछ मूल मान बाउंड नहीं होते। इस प्रकार, हम एक अलग दृष्टिकोण का उपयोग करेंगे और Q-टेबल को एक डिक्शनरी द्वारा प्रस्तुत करेंगे।

(state,action) जोड़ी का उपयोग डिक्शनरी की कुंजी के रूप में करें, और मान Q-टेबल प्रविष्टि मान से मेल खाता होगा। (कोड ब्लॉक 9)
```
Q = {}
actions = (0,1)

def qvalues(state):
    return [Q.get((state,a),0) for a in actions]
```
यहाँ हम एक फ़ंक्शन qvalues() भी परिभाषित करते हैं, जो एक दिए गए स्टेट के लिए सभी संभावित कार्यों से मेल खाने वाले Q-टेबल मानों की एक सूची लौटाता है। यदि प्रविष्टि Q-टेबल में मौजूद नहीं है, तो हम डिफ़ॉल्ट रूप से 0 लौटाएंगे।

चलिए Q-लर्निंग शुरू करते हैं

अब हम पीटर को संतुलन सिखाने के लिए तैयार हैं!

पहले, कुछ हाइपरपैरामीटर्स सेट करें: (कोड ब्लॉक 10)
```
# hyperparameters
alpha = 0.3
gamma = 0.9
epsilon = 0.90
```
यहाँ, alpha is the learning rate that defines to which extent we should adjust the current values of Q-Table at each step. In the previous lesson we started with 1, and then decreased alpha to lower values during training. In this example we will keep it constant just for simplicity, and you can experiment with adjusting alpha values later.

gamma is the discount factor that shows to which extent we should prioritize future reward over current reward.

epsilon is the exploration/exploitation factor that determines whether we should prefer exploration to exploitation or vice versa. In our algorithm, we will in epsilon percent of the cases select the next action according to Q-Table values, and in the remaining number of cases we will execute a random action. This will allow us to explore areas of the search space that we have never seen before.

✅ In terms of balancing - choosing random action (exploration) would act as a random punch in the wrong direction, and the pole would have to learn how to recover the balance from those "mistakes"

Improve the algorithm

We can also make two improvements to our algorithm from the previous lesson:

Calculate average cumulative reward, over a number of simulations. We will print the progress each 5000 iterations, and we will average out our cumulative reward over that period of time. It means that if we get more than 195 point - we can consider the problem solved, with even higher quality than required.
Calculate maximum average cumulative result, Qmax, and we will store the Q-Table corresponding to that result. When you run the training you will notice that sometimes the average cumulative result starts to drop, and we want to keep the values of Q-Table that correspond to the best model observed during training.

Collect all cumulative rewards at each simulation at rewards वेक्टर आगे की प्लॉटिंग के लिए। (कोड ब्लॉक 11)

def probs(v,eps=1e-4):
    v = v-v.min()+eps
    v = v/v.sum()
    return v

Qmax = 0
cum_rewards = []
rewards = []
for epoch in range(100000):
    obs = env.reset()
    done = False
    cum_reward=0
    # == do the simulation ==
    while not done:
        s = discretize(obs)
        if random.random()<epsilon:
            # exploitation - chose the action according to Q-Table probabilities
            v = probs(np.array(qvalues(s)))
            a = random.choices(actions,weights=v)[0]
        else:
            # exploration - randomly chose the action
            a = np.random.randint(env.action_space.n)

        obs, rew, done, info = env.step(a)
        cum_reward+=rew
        ns = discretize(obs)
        Q[(s,a)] = (1 - alpha) * Q.get((s,a),0) + alpha * (rew + gamma * max(qvalues(ns)))
    cum_rewards.append(cum_reward)
    rewards.append(cum_reward)
    # == Periodically print results and calculate average reward ==
    if epoch%5000==0:
        print(f"{epoch}: {np.average(cum_rewards)}, alpha={alpha}, epsilon={epsilon}")
        if np.average(cum_rewards) > Qmax:
            Qmax = np.average(cum_rewards)
            Qbest = Q
        cum_rewards=[]

आप उन परिणामों से क्या नोटिस कर सकते हैं:

हमारे लक्ष्य के करीब। हम 100+ लगातार सिमुलेशन रन के दौरान 195 संचयी रिवार्ड प्राप्त करने के लक्ष्य को प्राप्त करने के बहुत करीब हैं, या हम वास्तव में इसे प्राप्त कर चुके हो सकते हैं! भले ही हमें छोटे नंबर मिलें, हम अभी भी नहीं जानते, क्योंकि हम 5000 रन के औसत पर जा रहे हैं, और केवल 100 रन औपचारिक मानदंड में आवश्यक हैं।
रिवार्ड गिरना शुरू होता है। कभी-कभी रिवार्ड गिरना शुरू हो जाता है, जिसका मतलब है कि हम Q-टेबल में पहले से सीखे गए मानों को उन मानों से "नष्ट" कर सकते हैं जो स्थिति को बदतर बनाते हैं।

यह अवलोकन अधिक स्पष्ट रूप से दिखाई देता है यदि हम प्रशिक्षण प्रगति का ग्राफ़ बनाते हैं।

प्रशिक्षण प्रगति का ग्राफ़ बनाना

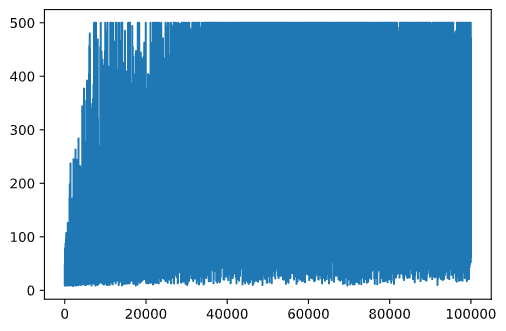
प्रशिक्षण के दौरान, हमने प्रत्येक पुनरावृत्ति में संचयी रिवार्ड मान को rewards वेक्टर में एकत्र किया है। यहाँ यह कैसा दिखता है जब हम इसे पुनरावृत्ति संख्या के खिलाफ प्लॉट करते हैं:

plt.plot(rewards)

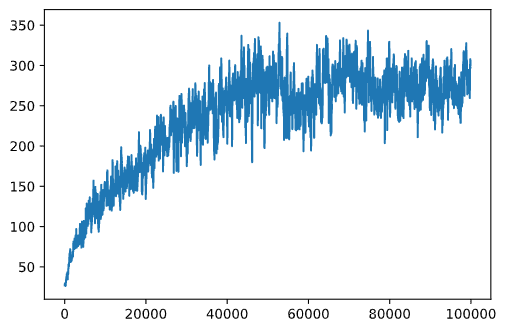
इस ग्राफ़ से, कुछ भी बताना संभव नहीं है, क्योंकि स्टोचैस्टिक प्रशिक्षण प्रक्रिया की प्रकृति के कारण प्रशिक्षण सत्रों की लंबाई बहुत भिन्न होती है। इस ग्राफ़ को अधिक समझने योग्य बनाने के लिए, हम प्रयोगों की एक श्रृंखला पर रनिंग एवरेज की गणना कर सकते हैं, कहें 100। इसे np.convolve का उपयोग करके आसानी से किया जा सकता है: (कोड ब्लॉक 12)

def running_average(x,window):
    return np.convolve(x,np.ones(window)/window,mode='valid')

plt.plot(running_average(rewards,100))

हाइपरपैरामीटर्स को बदलना

प्रशिक्षण को अधिक स्थिर बनाने के लिए, यह समझ में आता है कि हमारे कुछ हाइपरपैरामीटर्स को प्रशिक्षण के दौरान समायोजित किया जाए। विशेष रूप से:

लर्निंग रेट के लिए, alpha, we may start with values close to 1, and then keep decreasing the parameter. With time, we will be getting good probability values in the Q-Table, and thus we should be adjusting them slightly, and not overwriting completely with new values.
Increase epsilon. We may want to increase the epsilon slowly, in order to explore less and exploit more. It probably makes sense to start with lower value of epsilon, और लगभग 1 तक बढ़ें।

कार्य 1: हाइपरपैरामीटर मानों के साथ खेलें और देखें कि क्या आप उच्च संचयी रिवार्ड प्राप्त कर सकते हैं। क्या आप 195 से ऊपर जा रहे हैं?

कार्य 2: समस्या को औपचारिक रूप से हल करने के लिए, आपको 100 लगातार रन के दौरान 195 औसत रिवार्ड प्राप्त करने की आवश्यकता है। प्रशिक्षण के दौरान इसे मापें और सुनिश्चित करें कि आपने समस्या को औपचारिक रूप से हल कर लिया है!

परिणाम को क्रियान्वित में देखना

यह देखना दिलचस्प होगा कि प्रशिक्षित मॉडल वास्तव में कैसे व्यवहार करता है। चलिए सिमुलेशन चलाते हैं और Q-टेबल में संभाव्यता वितरण के अनुसार कार्य चयन रणनीति का पालन करते हैं: (कोड ब्लॉक 13)

obs = env.reset()
done = False
while not done:
   s = discretize(obs)
   env.render()
   v = probs(np.array(qvalues(s)))
   a = random.choices(actions,weights=v)[0]
   obs,_,done,_ = env.step(a)
env.close()

आपको कुछ ऐसा दिखना चाहिए:

🚀चुनौती

कार्य 3: यहाँ, हम Q-टेबल की अंतिम प्रति का उपयोग कर रहे थे, जो सबसे अच्छी नहीं हो सकती। याद रखें कि हमने सबसे अच्छा प्रदर्शन करने वाले Q-टेबल को Qbest variable! Try the same example with the best-performing Q-Table by copying Qbest over to Q and see if you notice the difference.

Task 4: Here we were not selecting the best action on each step, but rather sampling with corresponding probability distribution. Would it make more sense to always select the best action, with the highest Q-Table value? This can be done by using np.argmax फ़ंक्शन का उपयोग करके सबसे अधिक Q-टेबल मान से मेल खाने वाले कार्य संख्या को खोजने के लिए। इस रणनीति को लागू करें और देखें कि क्या यह संतुलन में सुधार करता है।

पोस्ट-लेक्चर क्विज़

असाइनमेंट

Train a Mountain Car

निष्कर्ष

अब हमने सीखा है कि एजेंटों को अच्छे परिणाम प्राप्त करने के लिए कैसे प्रशिक्षित किया जाए, बस उन्हें एक रिवार्ड फ़ंक्शन प्रदान करके जो खेल की वांछित स्थिति को परिभाषित करता है, और उन्हें खोज स्थान को बुद्धिमानी से अन्वेषण करने का अवसर देकर। हमने डिस्क्रीट और कंटीन्यूअस एनवायरनमेंट्स के मामलों में Q-लर्निंग एल्गोरिदम को सफलतापूर्वक लागू किया है, लेकिन डिस्क्रीट एक्शन्स के साथ।

यह अध्ययन करना भी महत्वपूर्ण है कि जब एक्शन स्टेट भी कंटीन्यूअस होता है, और जब ऑब्जर्वेशन स्पेस बहुत अधिक जटिल होता है, जैसे कि अटारी गेम स्क्रीन से छवि। उन समस्याओं में हमें अक्सर अच्छे परिणाम प्राप्त करने के लिए अधिक शक्तिशाली मशीन लर्निंग तकनीकों, जैसे कि न्यूरल नेटवर्क्स, का उपयोग करने की आवश्यकता होती है। ये अधिक उन्नत विषय हमारे आगामी अधिक उन्नत एआई कोर्स के विषय हैं।

अस्वीकरण: यह दस्तावेज़ मशीन-आधारित एआई अनुवाद सेवाओं का उपयोग करके अनुवादित किया गया है। जबकि हम सटीकता के लिए प्रयास करते हैं, कृपया ध्यान दें कि स्वचालित अनुवादों में त्रुटियाँ या अशुद्धियाँ हो सकती हैं। अपनी मूल भाषा में मूल दस्तावेज़ को आधिकारिक स्रोत माना जाना चाहिए। महत्वपूर्ण जानकारी के लिए, पेशेवर मानव अनुवाद की सिफारिश की जाती है। इस अनुवाद के उपयोग से उत्पन्न किसी भी गलतफहमी या गलत व्याख्या के लिए हम उत्तरदायी नहीं हैं।