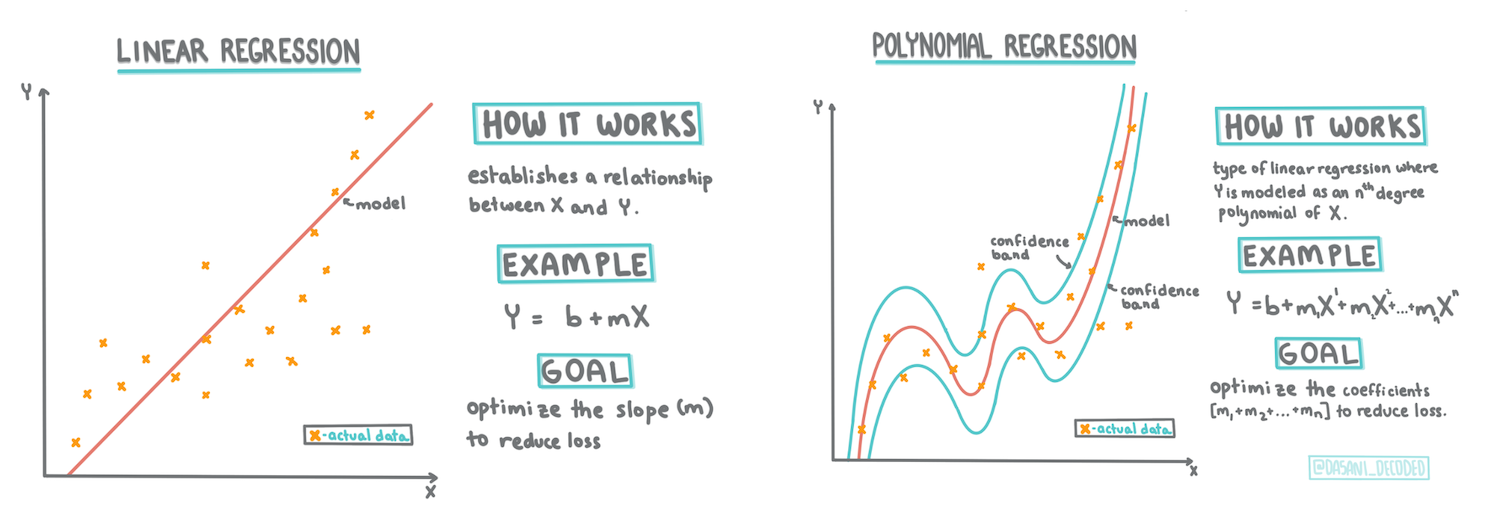
# Побудова моделі регресії за допомогою Scikit-learn: чотири способи регресії  > Інфографіка від [Dasani Madipalli](https://twitter.com/dasani_decoded) ## [Тест перед лекцією](https://ff-quizzes.netlify.app/en/ml/) > ### [Цей урок доступний у R!](../../../../2-Regression/3-Linear/solution/R/lesson_3.html) ### Вступ До цього моменту ви дослідили, що таке регресія, використовуючи вибіркові дані з набору даних про ціни на гарбузи, який ми будемо використовувати протягом цього уроку. Ви також візуалізували ці дані за допомогою Matplotlib. Тепер ви готові глибше зануритися в регресію для машинного навчання. Хоча візуалізація дозволяє зрозуміти дані, справжня сила машинного навчання полягає у _навчанні моделей_. Моделі навчаються на історичних даних, щоб автоматично захоплювати залежності між даними, і дозволяють прогнозувати результати для нових даних, які модель раніше не бачила. У цьому уроці ви дізнаєтеся більше про два типи регресії: _основну лінійну регресію_ та _поліноміальну регресію_, а також про деякі математичні основи цих методів. Ці моделі дозволять нам прогнозувати ціни на гарбузи залежно від різних вхідних даних. [](https://youtu.be/CRxFT8oTDMg "ML для початківців - Розуміння лінійної регресії") > 🎥 Натисніть на зображення вище, щоб переглянути короткий відеоогляд лінійної регресії. > Протягом цього курсу ми припускаємо мінімальні знання математики та прагнемо зробити її доступною для студентів з інших галузей, тому звертайте увагу на примітки, 🧮 математичні виклики, діаграми та інші навчальні інструменти для полегшення розуміння. ### Передумови На даний момент ви повинні бути знайомі зі структурою даних про гарбузи, які ми досліджуємо. Ви можете знайти їх попередньо завантаженими та очищеними у файлі _notebook.ipynb_ цього уроку. У файлі ціна гарбуза відображається за бушель у новому фреймі даних. Переконайтеся, що ви можете запускати ці ноутбуки в ядрах Visual Studio Code. ### Підготовка Нагадаємо, ви завантажуєте ці дані, щоб ставити запитання до них. - Коли найкращий час для купівлі гарбузів? - Яку ціну можна очікувати за ящик мініатюрних гарбузів? - Чи варто купувати їх у кошиках на півбушеля чи в коробках на 1 1/9 бушеля? Давайте продовжимо досліджувати ці дані. У попередньому уроці ви створили фрейм даних Pandas і заповнили його частиною оригінального набору даних, стандартизуючи ціни за бушель. Однак, зробивши це, ви змогли зібрати лише близько 400 точок даних і лише для осінніх місяців. Перегляньте дані, які ми попередньо завантажили у супровідному ноутбуці цього уроку. Дані попередньо завантажені, а початковий діаграма розсіювання побудована для відображення даних за місяцями. Можливо, ми зможемо отримати трохи більше деталей про природу даних, якщо очистимо їх більше. ## Лінія лінійної регресії Як ви дізналися в Уроці 1, мета вправи з лінійної регресії полягає в тому, щоб побудувати лінію для: - **Показу взаємозв'язків змінних**. Показати взаємозв'язок між змінними. - **Прогнозування**. Зробити точні прогнози щодо того, де нова точка даних буде розташована відносно цієї лінії. Зазвичай для побудови такого типу лінії використовується метод **регресії найменших квадратів**. Термін "найменші квадрати" означає, що всі точки даних навколо лінії регресії підносяться до квадрату, а потім додаються. Ідеально, щоб остаточна сума була якомога меншою, оскільки ми хочемо мати низьку кількість помилок, або `найменші квадрати`. Ми робимо це, оскільки хочемо змоделювати лінію, яка має найменшу сумарну відстань від усіх наших точок даних. Ми також підносимо терміни до квадрату перед додаванням, оскільки нас цікавить їх величина, а не напрямок. 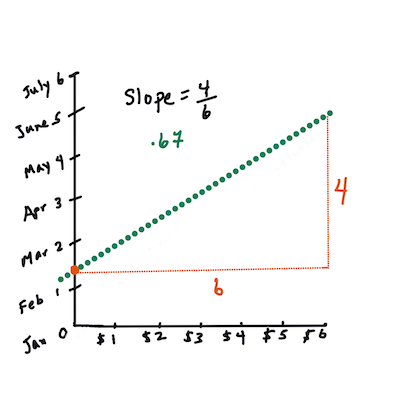> **🧮 Покажіть мені математику** > > Ця лінія, яка називається _лінією найкращого підходу_, може бути виражена [рівнянням](https://en.wikipedia.org/wiki/Simple_linear_regression): > > ``` > Y = a + bX > ``` > > `X` — це "пояснювальна змінна". `Y` — це "залежна змінна". Нахил лінії — це `b`, а `a` — це точка перетину з віссю Y, яка відповідає значенню `Y`, коли `X = 0`. > > > > Спочатку обчисліть нахил `b`. 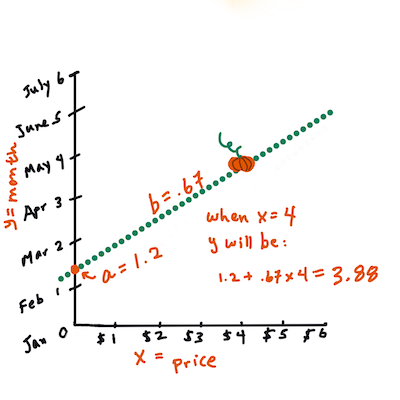Інфографіка від [Jen Looper](https://twitter.com/jenlooper) > > Іншими словами, звертаючись до початкового питання про дані гарбузів: "прогнозуйте ціну гарбуза за бушель за місяцями", `X` буде означати ціну, а `Y` — місяць продажу. > > > > Обчисліть значення Y. Якщо ви платите близько $4, це має бути квітень! Інфографіка від [Jen Looper](https://twitter.com/jenlooper) > > Математика, яка обчислює лінію, повинна демонструвати нахил лінії, який також залежить від точки перетину, або де `Y` розташований, коли `X = 0`. > > Ви можете ознайомитися з методом обчислення цих значень на веб-сайті [Math is Fun](https://www.mathsisfun.com/data/least-squares-regression.html). Також відвідайте [цей калькулятор найменших квадратів](https://www.mathsisfun.com/data/least-squares-calculator.html), щоб побачити, як значення чисел впливають на лінію. ## Кореляція Ще один термін, який потрібно зрозуміти, — це **коефіцієнт кореляції** між заданими змінними X і Y. Використовуючи діаграму розсіювання, ви можете швидко візуалізувати цей коефіцієнт. Діаграма з точками даних, розташованими в акуратній лінії, має високу кореляцію, але діаграма з точками даних, розкиданими між X і Y, має низьку кореляцію. Хороша модель лінійної регресії буде тією, яка має високий (ближче до 1, ніж до 0) коефіцієнт кореляції, використовуючи метод регресії найменших квадратів із лінією регресії. ✅ Запустіть ноутбук, що супроводжує цей урок, і подивіться на діаграму розсіювання "Місяць до Ціни". Чи здається, що дані, які асоціюють місяць із ціною продажу гарбузів, мають високу чи низьку кореляцію, згідно з вашим візуальним інтерпретацією діаграми розсіювання? Чи змінюється це, якщо використовувати більш детальний вимір замість `Місяць`, наприклад, *день року* (тобто кількість днів з початку року)? У наведеному нижче коді ми припускаємо, що ми очистили дані та отримали фрейм даних під назвою `new_pumpkins`, схожий на наступний: ID | Місяць | ДеньРоку | Сорт | Місто | Упаковка | Низька ціна | Висока ціна | Ціна ---|-------|-----------|---------|------|---------|-----------|------------|------- 70 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 15.0 | 15.0 | 13.636364 71 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 18.0 | 18.0 | 16.363636 72 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 18.0 | 18.0 | 16.363636 73 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 17.0 | 17.0 | 15.454545 74 | 10 | 281 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 15.0 | 15.0 | 13.636364 > Код для очищення даних доступний у [`notebook.ipynb`](../../../../2-Regression/3-Linear/notebook.ipynb). Ми виконали ті ж кроки очищення, що й у попередньому уроці, і обчислили стовпець `DayOfYear`, використовуючи наступний вираз: ```python day_of_year = pd.to_datetime(pumpkins['Date']).apply(lambda dt: (dt-datetime(dt.year,1,1)).days) ``` Тепер, коли ви розумієте математику, що лежить в основі лінійної регресії, давайте створимо модель регресії, щоб перевірити, чи можемо ми передбачити, яка упаковка гарбузів матиме найкращі ціни на гарбузи. Хтось, хто купує гарбузи для святкового гарбузового поля, може захотіти отримати цю інформацію, щоб оптимізувати свої покупки упаковок гарбузів для поля. ## Пошук кореляції [](https://youtu.be/uoRq-lW2eQo "ML для початківців - Пошук кореляції: ключ до лінійної регресії") > 🎥 Натисніть на зображення вище, щоб переглянути короткий відеоогляд кореляції. З попереднього уроку ви, мабуть, бачили, що середня ціна за різні місяці виглядає так: Це свідчить про те, що має бути певна кореляція, і ми можемо спробувати навчити модель лінійної регресії, щоб передбачити взаємозв'язок між `Місяць` і `Ціна`, або між `ДеньРоку` і `Ціна`. Ось діаграма розсіювання, яка показує останній взаємозв'язок: Давайте перевіримо, чи є кореляція, використовуючи функцію `corr`: ```python print(new_pumpkins['Month'].corr(new_pumpkins['Price'])) print(new_pumpkins['DayOfYear'].corr(new_pumpkins['Price'])) ``` Схоже, що кореляція досить мала, -0.15 за `Місяць` і -0.17 за `ДеньРоку`, але може бути інший важливий взаємозв'язок. Схоже, що є різні кластери цін, які відповідають різним сортам гарбузів. Щоб підтвердити цю гіпотезу, давайте побудуємо кожну категорію гарбузів, використовуючи різний колір. Передаючи параметр `ax` до функції побудови діаграми розсіювання, ми можемо побудувати всі точки на одному графіку: ```python ax=None colors = ['red','blue','green','yellow'] for i,var in enumerate(new_pumpkins['Variety'].unique()): df = new_pumpkins[new_pumpkins['Variety']==var] ax = df.plot.scatter('DayOfYear','Price',ax=ax,c=colors[i],label=var) ``` Наше дослідження свідчить про те, що сорт має більший вплив на загальну ціну, ніж фактична дата продажу. Ми можемо побачити це за допомогою стовпчастої діаграми: ```python new_pumpkins.groupby('Variety')['Price'].mean().plot(kind='bar') ``` Давайте зосередимося на даний момент лише на одному сорті гарбузів, "pie type", і подивимося, який вплив має дата на ціну: ```python pie_pumpkins = new_pumpkins[new_pumpkins['Variety']=='PIE TYPE'] pie_pumpkins.plot.scatter('DayOfYear','Price') ``` Якщо ми тепер обчислимо кореляцію між `Ціна` і `ДеньРоку`, використовуючи функцію `corr`, ми отримаємо щось близько `-0.27` - що означає, що навчання моделі прогнозування має сенс. > Перед навчанням моделі лінійної регресії важливо переконатися, що наші дані очищені. Лінійна регресія не працює добре з відсутніми значеннями, тому має сенс позбутися всіх порожніх клітинок: ```python pie_pumpkins.dropna(inplace=True) pie_pumpkins.info() ``` Інший підхід полягатиме в заповненні цих порожніх значень середніми значеннями з відповідного стовпця. ## Проста лінійна регресія [](https://youtu.be/e4c_UP2fSjg "ML для початківців - Лінійна та поліноміальна регресія за допомогою Scikit-learn") > 🎥 Натисніть на зображення вище, щоб переглянути короткий відеоогляд лінійної та поліноміальної регресії. Для навчання нашої моделі лінійної регресії ми будемо використовувати бібліотеку **Scikit-learn**. ```python from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error from sklearn.model_selection import train_test_split ``` Ми починаємо з розділення вхідних значень (особливостей) і очікуваного результату (мітки) на окремі масиви numpy: ```python X = pie_pumpkins['DayOfYear'].to_numpy().reshape(-1,1) y = pie_pumpkins['Price'] ``` > Зверніть увагу, що нам довелося виконати `reshape` для вхідних даних, щоб пакет лінійної регресії правильно їх зрозумів. Лінійна регресія очікує 2D-масив як вхідні дані, де кожен рядок масиву відповідає вектору вхідних особливостей. У нашому випадку, оскільки у нас є лише один вхід, нам потрібен масив із формою N×1, де N — це розмір набору даних. Потім нам потрібно розділити дані на навчальний і тестовий набори, щоб ми могли перевірити нашу модель після навчання: ```python X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) ``` Нарешті, навчання фактичної моделі лінійної регресії займає лише два рядки коду. Ми визначаємо об'єкт `LinearRegression` і підганяємо його до наших даних, використовуючи метод `fit`: ```python lin_reg = LinearRegression() lin_reg.fit(X_train,y_train) ``` Об'єкт `LinearRegression` після підгонки містить усі коефіцієнти регресії, до яких можна отримати доступ за допомогою властивості `.coef_`. У нашому випадку є лише один коефіцієнт, який має бути близько `-0.017`. Це означає, що ціни, здається, трохи падають з часом, але не надто сильно, приблизно на 2 центи на день. Ми також можемо отримати точку перетину регресії з віссю Y, використовуючи `lin_reg.intercept_` - вона буде близько `21` у нашому випадку, що вказує на ціну на початку року. Щоб побачити, наскільки точна наша модель, ми можемо прогнозувати ціни на тестовому набор Наша помилка, здається, зосереджена на 2 пунктах, що становить ~17%. Не надто добре. Ще одним показником якості моделі є **коефіцієнт детермінації**, який можна отримати таким чином: ```python score = lin_reg.score(X_train,y_train) print('Model determination: ', score) ``` Якщо значення дорівнює 0, це означає, що модель не враховує вхідні дані і діє як *найгірший лінійний прогнозатор*, який просто є середнім значенням результату. Значення 1 означає, що ми можемо ідеально передбачити всі очікувані результати. У нашому випадку коефіцієнт становить близько 0.06, що досить низько. Ми також можемо побудувати графік тестових даних разом із лінією регресії, щоб краще побачити, як регресія працює у нашому випадку: ```python plt.scatter(X_test,y_test) plt.plot(X_test,pred) ``` ## Поліноміальна регресія Іншим типом лінійної регресії є поліноміальна регресія. Хоча іноді існує лінійна залежність між змінними — чим більший об’єм гарбуза, тим вища ціна — іноді ці залежності не можна зобразити у вигляді площини або прямої лінії. ✅ Ось [кілька прикладів](https://online.stat.psu.edu/stat501/lesson/9/9.8) даних, які можуть використовувати поліноміальну регресію. Подивіться ще раз на залежність між датою та ціною. Чи здається цей розкид точок таким, що його обов’язково слід аналізувати прямою лінією? Хіба ціни не можуть коливатися? У цьому випадку можна спробувати поліноміальну регресію. ✅ Поліноми — це математичні вирази, які можуть складатися з однієї або кількох змінних і коефіцієнтів. Поліноміальна регресія створює криву, яка краще підходить для нелінійних даних. У нашому випадку, якщо ми включимо квадратну змінну `DayOfYear` у вхідні дані, ми зможемо підігнати наші дані під параболічну криву, яка матиме мінімум у певний момент протягом року. Scikit-learn включає зручний [API для конвеєра](https://scikit-learn.org/stable/modules/generated/sklearn.pipeline.make_pipeline.html?highlight=pipeline#sklearn.pipeline.make_pipeline), щоб об’єднати різні етапи обробки даних. **Конвеєр** — це ланцюжок **оцінювачів**. У нашому випадку ми створимо конвеєр, який спочатку додає поліноміальні ознаки до нашої моделі, а потім навчає регресію: ```python from sklearn.preprocessing import PolynomialFeatures from sklearn.pipeline import make_pipeline pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression()) pipeline.fit(X_train,y_train) ``` Використання `PolynomialFeatures(2)` означає, що ми включимо всі поліноми другого ступеня з вхідних даних. У нашому випадку це просто означатиме `DayOfYear`², але якщо є дві вхідні змінні X і Y, це додасть X², XY і Y². Ми також можемо використовувати поліноми вищого ступеня, якщо це необхідно. Конвеєри можна використовувати так само, як і оригінальний об’єкт `LinearRegression`, тобто ми можемо виконати `fit` для конвеєра, а потім використовувати `predict`, щоб отримати результати прогнозу. Ось графік, який показує тестові дані та криву апроксимації: Використовуючи поліноміальну регресію, ми можемо отримати трохи нижчий MSE і вищий коефіцієнт детермінації, але не значно. Нам потрібно врахувати інші ознаки! > Ви можете побачити, що мінімальні ціни на гарбузи для пирогів спостерігаються десь навколо Хелловіну. Як ви можете це пояснити? 🎃 Вітаємо, ви щойно створили модель, яка може допомогти передбачити ціну гарбузів для пирогів. Ви, ймовірно, можете повторити ту саму процедуру для всіх типів гарбузів, але це було б виснажливо. Давайте тепер навчимося враховувати різновиди гарбузів у нашій моделі! ## Категоріальні ознаки У ідеальному світі ми хочемо мати можливість передбачати ціни для різних різновидів гарбузів, використовуючи одну й ту саму модель. Однак стовпець `Variety` дещо відрізняється від таких стовпців, як `Month`, оскільки він містить нечислові значення. Такі стовпці називаються **категоріальними**. [](https://youtu.be/DYGliioIAE0 "ML для початківців - Прогнозування категоріальних ознак за допомогою лінійної регресії") > 🎥 Натисніть на зображення вище, щоб переглянути короткий відеоогляд використання категоріальних ознак. Ось як середня ціна залежить від різновиду: Щоб врахувати різновид, спочатку потрібно перетворити його у числову форму, або **закодувати**. Є кілька способів зробити це: * Просте **числове кодування** створить таблицю різних різновидів, а потім замінить назву різновиду на індекс у цій таблиці. Це не найкраща ідея для лінійної регресії, оскільки лінійна регресія бере фактичне числове значення індексу та додає його до результату, множачи на певний коефіцієнт. У нашому випадку залежність між номером індексу та ціною явно нелінійна, навіть якщо ми переконаємося, що індекси впорядковані певним чином. * **One-hot кодування** замінить стовпець `Variety` на 4 різні стовпці, по одному для кожного різновиду. Кожен стовпець міститиме `1`, якщо відповідний рядок належить до даного різновиду, і `0` в іншому випадку. Це означає, що в лінійній регресії буде чотири коефіцієнти, по одному для кожного різновиду гарбуза, які відповідають за "початкову ціну" (або скоріше "додаткову ціну") для цього конкретного різновиду. Код нижче показує, як ми можемо виконати one-hot кодування для різновиду: ```python pd.get_dummies(new_pumpkins['Variety']) ``` ID | FAIRYTALE | MINIATURE | MIXED HEIRLOOM VARIETIES | PIE TYPE ----|-----------|-----------|--------------------------|---------- 70 | 0 | 0 | 0 | 1 71 | 0 | 0 | 0 | 1 ... | ... | ... | ... | ... 1738 | 0 | 1 | 0 | 0 1739 | 0 | 1 | 0 | 0 1740 | 0 | 1 | 0 | 0 1741 | 0 | 1 | 0 | 0 1742 | 0 | 1 | 0 | 0 Щоб навчити лінійну регресію, використовуючи one-hot закодований різновид як вхідні дані, нам просто потрібно правильно ініціалізувати дані `X` і `y`: ```python X = pd.get_dummies(new_pumpkins['Variety']) y = new_pumpkins['Price'] ``` Решта коду така ж, як і той, що ми використовували вище для навчання лінійної регресії. Якщо ви спробуєте це, то побачите, що середньоквадратична помилка приблизно така ж, але ми отримуємо набагато вищий коефіцієнт детермінації (~77%). Щоб отримати ще точніші прогнози, ми можемо врахувати більше категоріальних ознак, а також числові ознаки, такі як `Month` або `DayOfYear`. Щоб отримати один великий масив ознак, ми можемо використати `join`: ```python X = pd.get_dummies(new_pumpkins['Variety']) \ .join(new_pumpkins['Month']) \ .join(pd.get_dummies(new_pumpkins['City'])) \ .join(pd.get_dummies(new_pumpkins['Package'])) y = new_pumpkins['Price'] ``` Тут ми також враховуємо `City` і тип `Package`, що дає нам MSE 2.84 (10%) і детермінацію 0.94! ## Об’єднання всього разом Щоб створити найкращу модель, ми можемо використовувати комбіновані (one-hot закодовані категоріальні + числові) дані з наведеного вище прикладу разом із поліноміальною регресією. Ось повний код для вашої зручності: ```python # set up training data X = pd.get_dummies(new_pumpkins['Variety']) \ .join(new_pumpkins['Month']) \ .join(pd.get_dummies(new_pumpkins['City'])) \ .join(pd.get_dummies(new_pumpkins['Package'])) y = new_pumpkins['Price'] # make train-test split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) # setup and train the pipeline pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression()) pipeline.fit(X_train,y_train) # predict results for test data pred = pipeline.predict(X_test) # calculate MSE and determination mse = np.sqrt(mean_squared_error(y_test,pred)) print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)') score = pipeline.score(X_train,y_train) print('Model determination: ', score) ``` Це має дати нам найкращий коефіцієнт детермінації майже 97% і MSE=2.23 (~8% помилки прогнозу). | Модель | MSE | Детермінація | |--------|-----|--------------| | `DayOfYear` Лінійна | 2.77 (17.2%) | 0.07 | | `DayOfYear` Поліноміальна | 2.73 (17.0%) | 0.08 | | `Variety` Лінійна | 5.24 (19.7%) | 0.77 | | Усі ознаки Лінійна | 2.84 (10.5%) | 0.94 | | Усі ознаки Поліноміальна | 2.23 (8.25%) | 0.97 | 🏆 Чудова робота! Ви створили чотири моделі регресії за один урок і покращили якість моделі до 97%. У фінальному розділі про регресію ви дізнаєтеся про логістичну регресію для визначення категорій. --- ## 🚀Завдання Перевірте кілька різних змінних у цьому ноутбуці, щоб побачити, як кореляція відповідає точності моделі. ## [Тест після лекції](https://ff-quizzes.netlify.app/en/ml/) ## Огляд і самостійне навчання У цьому уроці ми дізналися про лінійну регресію. Існують інші важливі типи регресії. Прочитайте про методи Stepwise, Ridge, Lasso і Elasticnet. Хороший курс для вивчення — [курс статистичного навчання Стенфорда](https://online.stanford.edu/courses/sohs-ystatslearning-statistical-learning). ## Завдання [Створіть модель](assignment.md) --- **Відмова від відповідальності**: Цей документ було перекладено за допомогою сервісу автоматичного перекладу [Co-op Translator](https://github.com/Azure/co-op-translator). Хоча ми прагнемо до точності, зверніть увагу, що автоматичні переклади можуть містити помилки або неточності. Оригінальний документ на його рідній мові слід вважати авторитетним джерелом. Для критично важливої інформації рекомендується професійний людський переклад. Ми не несемо відповідальності за будь-які непорозуміння або неправильні тлумачення, що виникли внаслідок використання цього перекладу.