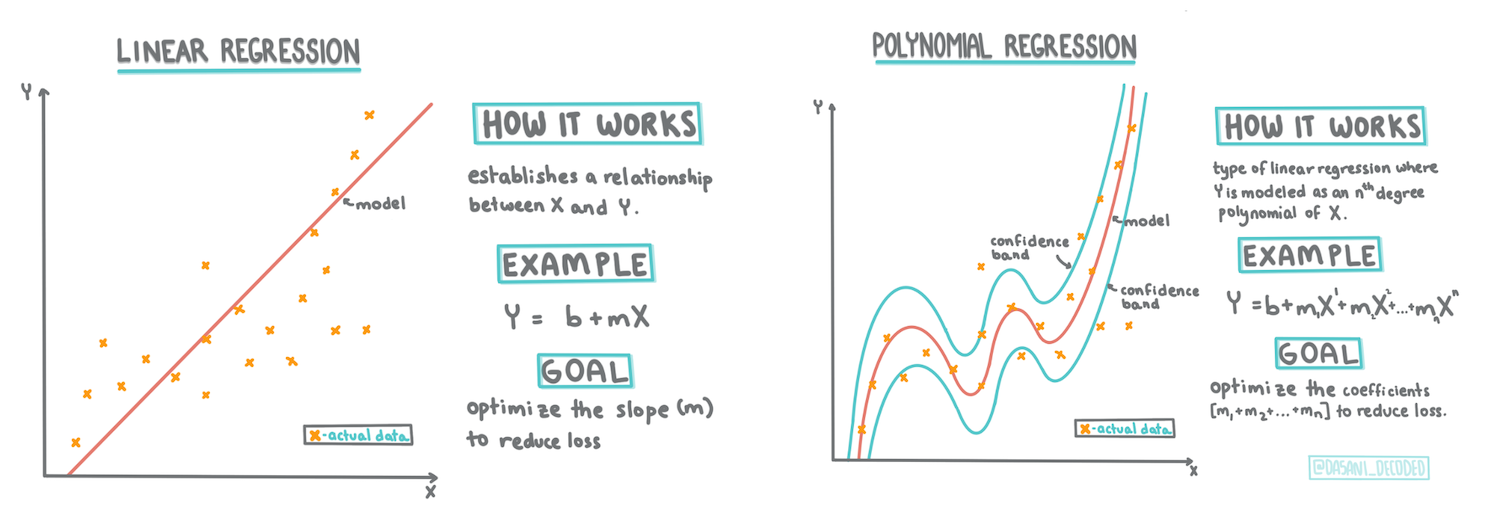
# สร้างโมเดลการถดถอยด้วย Scikit-learn: การถดถอย 4 วิธี  > อินโฟกราฟิกโดย [Dasani Madipalli](https://twitter.com/dasani_decoded) ## [แบบทดสอบก่อนเรียน](https://ff-quizzes.netlify.app/en/ml/) > ### [บทเรียนนี้มีในภาษา R ด้วย!](../../../../2-Regression/3-Linear/solution/R/lesson_3.html) ### บทนำ จนถึงตอนนี้ คุณได้สำรวจว่าการถดถอยคืออะไรโดยใช้ตัวอย่างข้อมูลจากชุดข้อมูลราคาฟักทองที่เราจะใช้ตลอดบทเรียนนี้ คุณยังได้สร้างภาพข้อมูลด้วย Matplotlib แล้ว ตอนนี้คุณพร้อมที่จะเจาะลึกเกี่ยวกับการถดถอยสำหรับการเรียนรู้ของเครื่อง (ML) การสร้างภาพช่วยให้คุณเข้าใจข้อมูล แต่พลังที่แท้จริงของการเรียนรู้ของเครื่องมาจาก _การฝึกโมเดล_ โมเดลถูกฝึกด้วยข้อมูลในอดีตเพื่อจับความสัมพันธ์ของข้อมูลโดยอัตโนมัติ และช่วยให้คุณคาดการณ์ผลลัพธ์สำหรับข้อมูลใหม่ที่โมเดลไม่เคยเห็นมาก่อน ในบทเรียนนี้ คุณจะได้เรียนรู้เพิ่มเติมเกี่ยวกับการถดถอยสองประเภท: _การถดถอยเชิงเส้นพื้นฐาน_ และ _การถดถอยพหุนาม_ พร้อมกับคณิตศาสตร์บางส่วนที่อยู่เบื้องหลังเทคนิคเหล่านี้ โมเดลเหล่านี้จะช่วยให้เราคาดการณ์ราคาฟักทองตามข้อมูลอินพุตที่แตกต่างกัน [](https://youtu.be/CRxFT8oTDMg "ML สำหรับผู้เริ่มต้น - เข้าใจการถดถอยเชิงเส้น") > 🎥 คลิกที่ภาพด้านบนเพื่อดูวิดีโอสั้น ๆ เกี่ยวกับการถดถอยเชิงเส้น > ตลอดหลักสูตรนี้ เราสมมติว่าคุณมีความรู้ทางคณิตศาสตร์เพียงเล็กน้อย และพยายามทำให้เข้าใจง่ายสำหรับนักเรียนที่มาจากสาขาอื่น ดังนั้นโปรดสังเกตบันทึก 🧮 คำอธิบายภาพ และเครื่องมือการเรียนรู้อื่น ๆ เพื่อช่วยในการทำความเข้าใจ ### ความรู้พื้นฐานที่ควรมี ตอนนี้คุณควรคุ้นเคยกับโครงสร้างของข้อมูลฟักทองที่เรากำลังตรวจสอบ คุณสามารถค้นหาข้อมูลนี้ที่โหลดไว้ล่วงหน้าและทำความสะอาดไว้ในไฟล์ _notebook.ipynb_ ของบทเรียนนี้ ในไฟล์นี้ ราคาฟักทองจะแสดงต่อบุชเชลใน DataFrame ใหม่ ตรวจสอบให้แน่ใจว่าคุณสามารถรันโน้ตบุ๊กเหล่านี้ในเคอร์เนลของ Visual Studio Code ได้ ### การเตรียมตัว เพื่อเป็นการทบทวน คุณกำลังโหลดข้อมูลนี้เพื่อถามคำถามเกี่ยวกับข้อมูล เช่น: - ช่วงเวลาใดที่ดีที่สุดในการซื้อฟักทอง? - ราคาที่คาดหวังสำหรับฟักทองขนาดเล็กหนึ่งกล่องคือเท่าไร? - ควรซื้อฟักทองในตะกร้าครึ่งบุชเชลหรือในกล่องขนาด 1 1/9 บุชเชล? มาดำดิ่งลงไปในข้อมูลนี้กันต่อ ในบทเรียนก่อน คุณได้สร้าง Pandas DataFrame และเติมข้อมูลบางส่วนจากชุดข้อมูลต้นฉบับ โดยการปรับมาตรฐานราคาต่อบุชเชล อย่างไรก็ตาม คุณสามารถรวบรวมข้อมูลได้เพียงประมาณ 400 จุดข้อมูล และเฉพาะในช่วงฤดูใบไม้ร่วงเท่านั้น ลองดูข้อมูลที่โหลดไว้ล่วงหน้าในโน้ตบุ๊กที่มาพร้อมกับบทเรียนนี้ ข้อมูลถูกโหลดไว้ล่วงหน้าและมีการสร้างกราฟกระจายเบื้องต้นเพื่อแสดงข้อมูลตามเดือน บางทีเราอาจได้รายละเอียดเพิ่มเติมเกี่ยวกับลักษณะของข้อมูลโดยการทำความสะอาดข้อมูลเพิ่มเติม ## เส้นการถดถอยเชิงเส้น ตามที่คุณได้เรียนรู้ในบทเรียนที่ 1 เป้าหมายของการถดถอยเชิงเส้นคือการวาดเส้นเพื่อ: - **แสดงความสัมพันธ์ของตัวแปร** แสดงความสัมพันธ์ระหว่างตัวแปร - **ทำการคาดการณ์** คาดการณ์ตำแหน่งของจุดข้อมูลใหม่ในความสัมพันธ์กับเส้นนั้นอย่างแม่นยำ โดยทั่วไป **Least-Squares Regression** จะใช้ในการวาดเส้นประเภทนี้ คำว่า 'least-squares' หมายถึงการนำจุดข้อมูลทั้งหมดรอบเส้นการถดถอยมายกกำลังสองและรวมเข้าด้วยกัน โดยอุดมคติแล้ว ผลรวมสุดท้ายควรมีค่าน้อยที่สุด เพราะเราต้องการข้อผิดพลาดที่น้อยที่สุด หรือ `least-squares` เราทำเช่นนี้เพราะเราต้องการสร้างโมเดลเส้นที่มีระยะทางสะสมจากจุดข้อมูลทั้งหมดน้อยที่สุด นอกจากนี้ เรายังยกกำลังสองก่อนรวมกันเพราะเราสนใจขนาดของค่ามากกว่าทิศทาง > **🧮 แสดงคณิตศาสตร์ให้ฉันดู** > > เส้นนี้เรียกว่า _เส้นที่เหมาะสมที่สุด_ สามารถแสดงได้ด้วย [สมการ](https://en.wikipedia.org/wiki/Simple_linear_regression): > > ``` > Y = a + bX > ``` > > `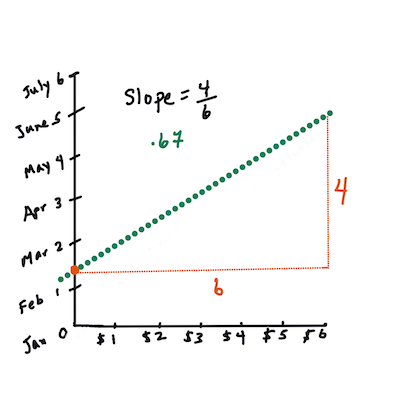X` คือ 'ตัวแปรอธิบาย' `Y` คือ 'ตัวแปรตาม' ความชันของเส้นคือ `b` และ `a` คือจุดตัดแกน Y ซึ่งหมายถึงค่าของ `Y` เมื่อ `X = 0` > > > > ขั้นแรก คำนวณความชัน `b` อินโฟกราฟิกโดย [Jen Looper](https://twitter.com/jenlooper) > > 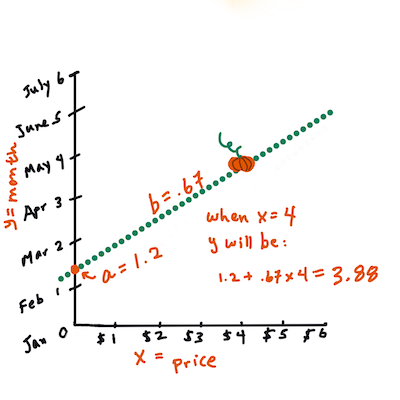กล่าวอีกนัยหนึ่ง และอ้างอิงจากคำถามดั้งเดิมของข้อมูลฟักทอง: "คาดการณ์ราคาฟักทองต่อบุชเชลตามเดือน" `X` จะหมายถึงราคา และ `Y` จะหมายถึงเดือนที่ขาย > > > > คำนวณค่าของ Y ถ้าคุณจ่ายประมาณ $4 นั่นอาจเป็นเดือนเมษายน! อินโฟกราฟิกโดย [Jen Looper](https://twitter.com/jenlooper) > > คณิตศาสตร์ที่คำนวณเส้นต้องแสดงความชันของเส้น ซึ่งขึ้นอยู่กับจุดตัดแกนด้วย หรือค่าที่ `Y` อยู่เมื่อ `X = 0` > > คุณสามารถดูวิธีการคำนวณค่าต่าง ๆ เหล่านี้ได้ที่เว็บไซต์ [Math is Fun](https://www.mathsisfun.com/data/least-squares-regression.html) และเยี่ยมชม [เครื่องคำนวณ Least-squares](https://www.mathsisfun.com/data/least-squares-calculator.html) เพื่อดูว่าค่าต่าง ๆ ส่งผลต่อเส้นอย่างไร ## ความสัมพันธ์ อีกคำหนึ่งที่ควรเข้าใจคือ **ค่าสัมประสิทธิ์ความสัมพันธ์** ระหว่างตัวแปร X และ Y ที่กำหนด การใช้กราฟกระจาย คุณสามารถมองเห็นค่าสัมประสิทธิ์นี้ได้อย่างรวดเร็ว กราฟที่มีจุดข้อมูลกระจายเป็นเส้นเรียบมีความสัมพันธ์สูง แต่กราฟที่มีจุดข้อมูลกระจายไปทั่วระหว่าง X และ Y มีความสัมพันธ์ต่ำ โมเดลการถดถอยเชิงเส้นที่ดีจะเป็นโมเดลที่มีค่าสัมประสิทธิ์ความสัมพันธ์สูง (ใกล้ 1 มากกว่า 0) โดยใช้วิธี Least-Squares Regression พร้อมเส้นการถดถอย ✅ รันโน้ตบุ๊กที่มาพร้อมกับบทเรียนนี้และดูกราฟกระจายของข้อมูลเดือนกับราคา ข้อมูลที่เชื่อมโยงเดือนกับราคาสำหรับการขายฟักทองดูเหมือนจะมีความสัมพันธ์สูงหรือต่ำตามการตีความด้วยสายตาของคุณ? ความสัมพันธ์นั้นเปลี่ยนไปหรือไม่หากคุณใช้มาตรการที่ละเอียดกว่า เช่น *วันในปี* (เช่น จำนวนวันตั้งแต่ต้นปี)? ในโค้ดด้านล่าง เราจะสมมติว่าเราได้ทำความสะอาดข้อมูลแล้ว และได้ DataFrame ที่เรียกว่า `new_pumpkins` ซึ่งมีลักษณะดังนี้: ID | Month | DayOfYear | Variety | City | Package | Low Price | High Price | Price ---|-------|-----------|---------|------|---------|-----------|------------|------- 70 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 15.0 | 15.0 | 13.636364 71 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 18.0 | 18.0 | 16.363636 72 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 18.0 | 18.0 | 16.363636 73 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 17.0 | 17.0 | 15.454545 74 | 10 | 281 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 15.0 | 15.0 | 13.636364 > โค้ดสำหรับทำความสะอาดข้อมูลมีอยู่ใน [`notebook.ipynb`](../../../../2-Regression/3-Linear/notebook.ipynb) เราได้ทำตามขั้นตอนการทำความสะอาดเดียวกับในบทเรียนก่อน และได้คำนวณคอลัมน์ `DayOfYear` โดยใช้สูตรต่อไปนี้: ```python day_of_year = pd.to_datetime(pumpkins['Date']).apply(lambda dt: (dt-datetime(dt.year,1,1)).days) ``` เมื่อคุณเข้าใจคณิตศาสตร์เบื้องหลังการถดถอยเชิงเส้นแล้ว มาสร้างโมเดลการถดถอยเพื่อดูว่าเราสามารถคาดการณ์ได้หรือไม่ว่าชุดฟักทองใดจะมีราคาที่ดีที่สุดสำหรับฟักทอง ผู้ที่ซื้อฟักทองสำหรับแปลงฟักทองในวันหยุดอาจต้องการข้อมูลนี้เพื่อเพิ่มประสิทธิภาพการซื้อชุดฟักทองสำหรับแปลง ## การมองหาความสัมพันธ์ [](https://youtu.be/uoRq-lW2eQo "ML สำหรับผู้เริ่มต้น - การมองหาความสัมพันธ์: กุญแจสู่การถดถอยเชิงเส้น") > 🎥 คลิกที่ภาพด้านบนเพื่อดูวิดีโอสั้น ๆ เกี่ยวกับความสัมพันธ์ จากบทเรียนก่อน คุณอาจเห็นว่าราคาเฉลี่ยสำหรับแต่ละเดือนมีลักษณะดังนี้: สิ่งนี้ชี้ให้เห็นว่าควรมีความสัมพันธ์บางอย่าง และเราสามารถลองฝึกโมเดลการถดถอยเชิงเส้นเพื่อคาดการณ์ความสัมพันธ์ระหว่าง `Month` และ `Price` หรือระหว่าง `DayOfYear` และ `Price` นี่คือกราฟกระจายที่แสดงความสัมพันธ์หลัง: มาดูกันว่ามีความสัมพันธ์หรือไม่โดยใช้ฟังก์ชัน `corr`: ```python print(new_pumpkins['Month'].corr(new_pumpkins['Price'])) print(new_pumpkins['DayOfYear'].corr(new_pumpkins['Price'])) ``` ดูเหมือนว่าความสัมพันธ์จะค่อนข้างต่ำ -0.15 โดย `Month` และ -0.17 โดย `DayOfMonth` แต่ก็อาจมีความสัมพันธ์ที่สำคัญอื่น ๆ ดูเหมือนว่าจะมีคลัสเตอร์ราคาที่แตกต่างกันซึ่งสอดคล้องกับพันธุ์ฟักทองที่แตกต่างกัน เพื่อยืนยันสมมติฐานนี้ ลองพล็อตแต่ละหมวดหมู่ฟักทองโดยใช้สีที่แตกต่างกัน โดยการส่งพารามิเตอร์ `ax` ไปยังฟังก์ชัน `scatter` เราสามารถพล็อตจุดทั้งหมดในกราฟเดียวกัน: ```python ax=None colors = ['red','blue','green','yellow'] for i,var in enumerate(new_pumpkins['Variety'].unique()): df = new_pumpkins[new_pumpkins['Variety']==var] ax = df.plot.scatter('DayOfYear','Price',ax=ax,c=colors[i],label=var) ``` การตรวจสอบของเราชี้ให้เห็นว่าพันธุ์มีผลต่อราคามากกว่าวันที่ขาย เราสามารถเห็นสิ่งนี้ได้จากกราฟแท่ง: ```python new_pumpkins.groupby('Variety')['Price'].mean().plot(kind='bar') ``` ให้เรามุ่งเน้นไปที่พันธุ์ฟักทองชนิดเดียวคือ 'pie type' และดูว่าผลของวันที่มีต่อราคาเป็นอย่างไร: ```python pie_pumpkins = new_pumpkins[new_pumpkins['Variety']=='PIE TYPE'] pie_pumpkins.plot.scatter('DayOfYear','Price') ``` หากเราคำนวณความสัมพันธ์ระหว่าง `Price` และ `DayOfYear` โดยใช้ฟังก์ชัน `corr` ตอนนี้ เราจะได้ค่าประมาณ `-0.27` - ซึ่งหมายความว่าการฝึกโมเดลการคาดการณ์มีเหตุผล > ก่อนการฝึกโมเดลการถดถอยเชิงเส้น สิ่งสำคัญคือต้องแน่ใจว่าข้อมูลของเราสะอาด การถดถอยเชิงเส้นไม่ทำงานได้ดีนักกับค่าที่ขาดหายไป ดังนั้นจึงสมควรที่จะลบเซลล์ว่างทั้งหมด: ```python pie_pumpkins.dropna(inplace=True) pie_pumpkins.info() ``` อีกวิธีหนึ่งคือเติมค่าที่ว่างเปล่าด้วยค่ามeanจากคอลัมน์ที่เกี่ยวข้อง ## การถดถอยเชิงเส้นแบบง่าย [](https://youtu.be/e4c_UP2fSjg "ML สำหรับผู้เริ่มต้น - การถดถอยเชิงเส้นและพหุนามด้วย Scikit-learn") > 🎥 คลิกที่ภาพด้านบนเพื่อดูวิดีโอสั้น ๆ เกี่ยวกับการถดถอยเชิงเส้นและพหุนาม ในการฝึกโมเดลการถดถอยเชิงเส้น เราจะใช้ไลบรารี **Scikit-learn** ```python from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error from sklearn.model_selection import train_test_split ``` เริ่มต้นด้วยการแยกค่าข้อมูลอินพุต (features) และผลลัพธ์ที่คาดหวัง (label) ออกเป็นอาเรย์ numpy แยกกัน: ```python X = pie_pumpkins['DayOfYear'].to_numpy().reshape(-1,1) y = pie_pumpkins['Price'] ``` > โปรดทราบว่าเราต้องใช้ `reshape` กับข้อมูลอินพุตเพื่อให้แพ็กเกจ Linear Regression เข้าใจได้อย่างถูกต้อง Linear Regression คาดหวังอาเรย์ 2 มิติเป็นอินพุต โดยที่แต่ละแถวของอาเรย์สอดคล้องกับเวกเตอร์ของฟีเจอร์อินพุต ในกรณีของเรา เนื่องจากเรามีอินพุตเพียงหนึ่งตัว - เราต้องการอาเรย์ที่มีรูปร่าง N×1 โดยที่ N คือขนาดของชุดข้อมูล จากนั้น เราต้องแบ่งข้อมูลออกเป็นชุดข้อมูลการฝึกและการทดสอบ เพื่อให้เราสามารถตรวจสอบความถูกต้องของโมเดลหลังการฝึกได้: ```python X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) ``` สุดท้าย การฝึกโมเดลการถดถอยเชิงเส้นจริงใช้เพียงสองบรรทัดโค้ด เรากำหนดออบเจ็กต์ `LinearRegression` และปรับให้เข้ากับข้อมูลของเราโดยใช้เมธอด `fit`: ```python lin_reg = LinearRegression() lin_reg.fit(X_train,y_train) ``` ออบเจ็กต์ `LinearRegression` หลังจาก `fit` จะมีสัมประสิทธิ์ทั้งหมดของการถดถอย ซึ่งสามารถเข้าถึงได้โดยใช้คุณสมบัติ `.coef_` ในกรณีของเรา มีเพียงสัมประสิทธิ์เดียว ซึ่งควรอยู่ที่ประมาณ `-0.017` ซึ่งหมายความว่าราคาดูเหมือนจะลดลงเล็กน้อยตามเวลา แต่ไม่มากนัก ประมาณ 2 เซนต์ต่อวัน นอกจากนี้เรายังสามารถเข้าถึงจุดตัดแกน Y ของการถดถอยได้โดยใช้ `lin_reg.intercept_` - ซึ่งจะอยู่ที่ประมาณ `21` ในกรณีของเรา ซึ่งบ่งชี้ถึงราคาต้นปี เพื่อดูว่าโมเดลของเรามีความแม่นยำเพียงใด เราสามารถคาดการณ์ราคาบนชุดข้อมูลทดสอบ และวัดว่าการคาดการณ์ของเราใกล้เคียงกับค่าที่คาดหวังเพียงใด สิ่งนี้สามารถทำได้โดยใช้เมตริก Mean Square Error (MSE) ซึ่งเป็นค่าเฉลี่ยของผลต่างกำลังสองทั้งหมดระหว่างค่าที่คาดหวังและค่าที่คาดการณ์ ```python pred = lin_reg.predict(X_test) mse = np.sqrt(mean_squared_error(y_test,pred)) print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)') ``` ข้อผิดพลาดของเราดูเหมือนจะอยู่ที่ประมาณ 2 จุด ซึ่งคิดเป็น ~17% ไม่ค่อยดีนัก ตัวบ่งชี้อีกตัวหนึ่งของคุณภาพโมเดลคือ **ค่าสัมประสิทธิ์การกำหนด** ซึ่งสามารถหาได้ดังนี้: ```python score = lin_reg.score(X_train,y_train) print('Model determination: ', score) ``` หากค่ามีค่าเท่ากับ 0 หมายความว่าโมเดลไม่ได้คำนึงถึงข้อมูลนำเข้า และทำหน้าที่เป็น *ตัวทำนายเชิงเส้นที่แย่ที่สุด* ซึ่งเป็นเพียงค่าเฉลี่ยของผลลัพธ์เท่านั้น ค่าที่เท่ากับ 1 หมายความว่าเราสามารถทำนายผลลัพธ์ที่คาดหวังได้อย่างสมบูรณ์แบบ ในกรณีของเรา ค่าสัมประสิทธิ์อยู่ที่ประมาณ 0.06 ซึ่งค่อนข้างต่ำ เรายังสามารถสร้างกราฟข้อมูลทดสอบพร้อมกับเส้นการถดถอยเพื่อดูว่าการถดถอยทำงานอย่างไรในกรณีของเรา: ```python plt.scatter(X_test,y_test) plt.plot(X_test,pred) ``` ## การถดถอยเชิงพหุนาม อีกประเภทหนึ่งของการถดถอยเชิงเส้นคือการถดถอยเชิงพหุนาม บางครั้งความสัมพันธ์ระหว่างตัวแปรอาจเป็นเชิงเส้น เช่น ยิ่งฟักทองมีปริมาตรมาก ราคาก็ยิ่งสูงขึ้น แต่บางครั้งความสัมพันธ์เหล่านี้ไม่สามารถวาดเป็นระนาบหรือเส้นตรงได้ ✅ [ตัวอย่างเพิ่มเติม](https://online.stat.psu.edu/stat501/lesson/9/9.8) ของข้อมูลที่สามารถใช้การถดถอยเชิงพหุนาม ลองดูความสัมพันธ์ระหว่างวันที่และราคาอีกครั้ง กราฟกระจายนี้ดูเหมือนควรจะวิเคราะห์ด้วยเส้นตรงหรือไม่? ราคาสามารถผันผวนได้หรือไม่? ในกรณีนี้ คุณสามารถลองใช้การถดถอยเชิงพหุนาม ✅ พหุนามเป็นนิพจน์ทางคณิตศาสตร์ที่อาจประกอบด้วยตัวแปรและสัมประสิทธิ์หนึ่งตัวหรือมากกว่า การถดถอยเชิงพหุนามสร้างเส้นโค้งเพื่อให้เหมาะสมกับข้อมูลที่ไม่เป็นเชิงเส้นได้ดียิ่งขึ้น ในกรณีของเรา หากเรารวมตัวแปร `DayOfYear` กำลังสองเข้าไปในข้อมูลนำเข้า เราควรจะสามารถปรับข้อมูลของเราให้เข้ากับเส้นโค้งพาราโบลา ซึ่งจะมีค่าต่ำสุดในช่วงเวลาหนึ่งของปี Scikit-learn มี [API pipeline](https://scikit-learn.org/stable/modules/generated/sklearn.pipeline.make_pipeline.html?highlight=pipeline#sklearn.pipeline.make_pipeline) ที่มีประโยชน์สำหรับการรวมขั้นตอนต่างๆ ของการประมวลผลข้อมูลเข้าด้วยกัน **Pipeline** คือชุดของ **estimators** ในกรณีของเรา เราจะสร้าง pipeline ที่เพิ่มคุณสมบัติพหุนามให้กับโมเดลของเรา และฝึกการถดถอย: ```python from sklearn.preprocessing import PolynomialFeatures from sklearn.pipeline import make_pipeline pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression()) pipeline.fit(X_train,y_train) ``` การใช้ `PolynomialFeatures(2)` หมายความว่าเราจะรวมพหุนามระดับสองทั้งหมดจากข้อมูลนำเข้า ในกรณีของเราจะหมายถึงเพียง `DayOfYear`² แต่หากมีตัวแปรนำเข้าสองตัว X และ Y จะเพิ่ม X², XY และ Y² เราอาจใช้พหุนามระดับสูงกว่านี้หากต้องการ Pipeline สามารถใช้งานได้ในลักษณะเดียวกับวัตถุ `LinearRegression` ดั้งเดิม เช่น เราสามารถ `fit` pipeline และใช้ `predict` เพื่อรับผลการทำนาย นี่คือกราฟที่แสดงข้อมูลทดสอบและเส้นโค้งประมาณค่า: การใช้การถดถอยเชิงพหุนาม เราสามารถลดค่า MSE และเพิ่มค่าสัมประสิทธิ์การกำหนดได้เล็กน้อย แต่ไม่มากนัก เราจำเป็นต้องพิจารณาคุณสมบัติอื่นๆ ด้วย! > คุณจะเห็นว่าราคาฟักทองต่ำสุดจะอยู่ประมาณวันฮาโลวีน คุณจะอธิบายเรื่องนี้ได้อย่างไร? 🎃 ยินดีด้วย คุณเพิ่งสร้างโมเดลที่สามารถช่วยทำนายราคาฟักทองสำหรับทำพาย คุณอาจทำขั้นตอนเดียวกันนี้ซ้ำสำหรับฟักทองทุกประเภท แต่จะค่อนข้างน่าเบื่อ มาเรียนรู้วิธีนำประเภทฟักทองมาพิจารณาในโมเดลของเรากันเถอะ! ## คุณสมบัติประเภทหมวดหมู่ ในโลกอุดมคติ เราต้องการสามารถทำนายราคาสำหรับฟักทองหลากหลายประเภทโดยใช้โมเดลเดียว อย่างไรก็ตาม คอลัมน์ `Variety` นั้นแตกต่างจากคอลัมน์อย่าง `Month` เพราะมันมีค่าที่ไม่ใช่ตัวเลข คอลัมน์เหล่านี้เรียกว่า **หมวดหมู่** [](https://youtu.be/DYGliioIAE0 "ML for beginners - Categorical Feature Predictions with Linear Regression") > 🎥 คลิกที่ภาพด้านบนเพื่อดูวิดีโอสั้นๆ เกี่ยวกับการใช้คุณสมบัติประเภทหมวดหมู่ นี่คือกราฟที่แสดงให้เห็นว่าราคาเฉลี่ยขึ้นอยู่กับประเภทฟักทองอย่างไร: เพื่อพิจารณาประเภทฟักทอง เราต้องแปลงมันเป็นรูปแบบตัวเลขก่อน หรือ **เข้ารหัส** มีหลายวิธีที่เราสามารถทำได้: * การเข้ารหัสตัวเลขแบบง่ายจะสร้างตารางของประเภทฟักทองต่างๆ และแทนที่ชื่อประเภทฟักทองด้วยดัชนีในตารางนั้น วิธีนี้ไม่เหมาะสำหรับการถดถอยเชิงเส้น เพราะการถดถอยเชิงเส้นจะใช้ค่าตัวเลขของดัชนีจริงๆ และเพิ่มเข้าไปในผลลัพธ์โดยการคูณด้วยสัมประสิทธิ์ ในกรณีของเรา ความสัมพันธ์ระหว่างหมายเลขดัชนีและราคานั้นชัดเจนว่าไม่เป็นเชิงเส้น แม้ว่าเราจะจัดลำดับดัชนีในลักษณะเฉพาะก็ตาม * **การเข้ารหัสแบบ one-hot** จะเปลี่ยนคอลัมน์ `Variety` เป็น 4 คอลัมน์ที่แตกต่างกัน หนึ่งคอลัมน์สำหรับแต่ละประเภทฟักทอง แต่ละคอลัมน์จะมีค่า `1` หากแถวที่เกี่ยวข้องเป็นประเภทฟักทองนั้น และ `0` หากไม่ใช่ นั่นหมายความว่าจะมีสัมประสิทธิ์สี่ตัวในการถดถอยเชิงเส้น หนึ่งตัวสำหรับแต่ละประเภทฟักทอง ซึ่งรับผิดชอบ "ราคาเริ่มต้น" (หรือ "ราคาที่เพิ่มขึ้น") สำหรับประเภทนั้นๆ โค้ดด้านล่างแสดงวิธีการเข้ารหัสแบบ one-hot สำหรับประเภทฟักทอง: ```python pd.get_dummies(new_pumpkins['Variety']) ``` ID | FAIRYTALE | MINIATURE | MIXED HEIRLOOM VARIETIES | PIE TYPE ----|-----------|-----------|--------------------------|---------- 70 | 0 | 0 | 0 | 1 71 | 0 | 0 | 0 | 1 ... | ... | ... | ... | ... 1738 | 0 | 1 | 0 | 0 1739 | 0 | 1 | 0 | 0 1740 | 0 | 1 | 0 | 0 1741 | 0 | 1 | 0 | 0 1742 | 0 | 1 | 0 | 0 เพื่อฝึกการถดถอยเชิงเส้นโดยใช้ประเภทฟักทองที่เข้ารหัสแบบ one-hot เป็นข้อมูลนำเข้า เราเพียงแค่ต้องกำหนดข้อมูล `X` และ `y` ให้ถูกต้อง: ```python X = pd.get_dummies(new_pumpkins['Variety']) y = new_pumpkins['Price'] ``` โค้ดที่เหลือเหมือนกับที่เราใช้ด้านบนเพื่อฝึกการถดถอยเชิงเส้น หากคุณลอง คุณจะเห็นว่าค่า MSE ใกล้เคียงกัน แต่เราจะได้ค่าสัมประสิทธิ์การกำหนดที่สูงขึ้น (~77%) เพื่อให้การทำนายแม่นยำยิ่งขึ้น เราสามารถนำคุณสมบัติประเภทหมวดหมู่อื่นๆ มาพิจารณา รวมถึงคุณสมบัติตัวเลข เช่น `Month` หรือ `DayOfYear` เพื่อสร้างชุดข้อมูลคุณสมบัติขนาดใหญ่ เราสามารถใช้ `join`: ```python X = pd.get_dummies(new_pumpkins['Variety']) \ .join(new_pumpkins['Month']) \ .join(pd.get_dummies(new_pumpkins['City'])) \ .join(pd.get_dummies(new_pumpkins['Package'])) y = new_pumpkins['Price'] ``` ที่นี่เรายังพิจารณา `City` และประเภท `Package` ซึ่งให้ค่า MSE 2.84 (10%) และค่าสัมประสิทธิ์การกำหนด 0.94! ## รวมทุกอย่างเข้าด้วยกัน เพื่อสร้างโมเดลที่ดีที่สุด เราสามารถใช้ข้อมูลที่รวมกัน (ประเภทหมวดหมู่ที่เข้ารหัสแบบ one-hot + ตัวเลข) จากตัวอย่างด้านบนร่วมกับการถดถอยเชิงพหุนาม นี่คือโค้ดทั้งหมดเพื่อความสะดวกของคุณ: ```python # set up training data X = pd.get_dummies(new_pumpkins['Variety']) \ .join(new_pumpkins['Month']) \ .join(pd.get_dummies(new_pumpkins['City'])) \ .join(pd.get_dummies(new_pumpkins['Package'])) y = new_pumpkins['Price'] # make train-test split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) # setup and train the pipeline pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression()) pipeline.fit(X_train,y_train) # predict results for test data pred = pipeline.predict(X_test) # calculate MSE and determination mse = np.sqrt(mean_squared_error(y_test,pred)) print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)') score = pipeline.score(X_train,y_train) print('Model determination: ', score) ``` สิ่งนี้ควรให้ค่าสัมประสิทธิ์การกำหนดที่ดีที่สุดเกือบ 97% และ MSE=2.23 (~8% ข้อผิดพลาดในการทำนาย) | โมเดล | MSE | ค่าสัมประสิทธิ์การกำหนด | |-------|-----|---------------------------| | `DayOfYear` Linear | 2.77 (17.2%) | 0.07 | | `DayOfYear` Polynomial | 2.73 (17.0%) | 0.08 | | `Variety` Linear | 5.24 (19.7%) | 0.77 | | All features Linear | 2.84 (10.5%) | 0.94 | | All features Polynomial | 2.23 (8.25%) | 0.97 | 🏆 ยอดเยี่ยม! คุณสร้างโมเดลการถดถอย 4 โมเดลในบทเรียนเดียว และปรับปรุงคุณภาพโมเดลได้ถึง 97% ในส่วนสุดท้ายเกี่ยวกับการถดถอย คุณจะได้เรียนรู้เกี่ยวกับการถดถอยโลจิสติกเพื่อกำหนดหมวดหมู่ --- ## 🚀ความท้าทาย ทดสอบตัวแปรต่างๆ ในโน้ตบุ๊กนี้เพื่อดูว่าความสัมพันธ์สอดคล้องกับความแม่นยำของโมเดลอย่างไร ## [แบบทดสอบหลังการบรรยาย](https://ff-quizzes.netlify.app/en/ml/) ## ทบทวนและศึกษาด้วยตนเอง ในบทเรียนนี้เราได้เรียนรู้เกี่ยวกับการถดถอยเชิงเส้น ยังมีประเภทการถดถอยที่สำคัญอื่นๆ อ่านเกี่ยวกับเทคนิค Stepwise, Ridge, Lasso และ Elasticnet หลักสูตรที่ดีในการศึกษาเพิ่มเติมคือ [Stanford Statistical Learning course](https://online.stanford.edu/courses/sohs-ystatslearning-statistical-learning) ## งานที่ได้รับมอบหมาย [สร้างโมเดล](assignment.md) --- **ข้อจำกัดความรับผิดชอบ**: เอกสารนี้ได้รับการแปลโดยใช้บริการแปลภาษา AI [Co-op Translator](https://github.com/Azure/co-op-translator) แม้ว่าเราจะพยายามให้การแปลมีความถูกต้อง แต่โปรดทราบว่าการแปลอัตโนมัติอาจมีข้อผิดพลาดหรือความไม่แม่นยำ เอกสารต้นฉบับในภาษาดั้งเดิมควรถือเป็นแหล่งข้อมูลที่เชื่อถือได้ สำหรับข้อมูลที่สำคัญ แนะนำให้ใช้บริการแปลภาษาจากผู้เชี่ยวชาญ เราไม่รับผิดชอบต่อความเข้าใจผิดหรือการตีความที่ผิดพลาดซึ่งเกิดจากการใช้การแปลนี้