# Ustvarjanje regresijskega modela s Scikit-learn: štiri načini regresije
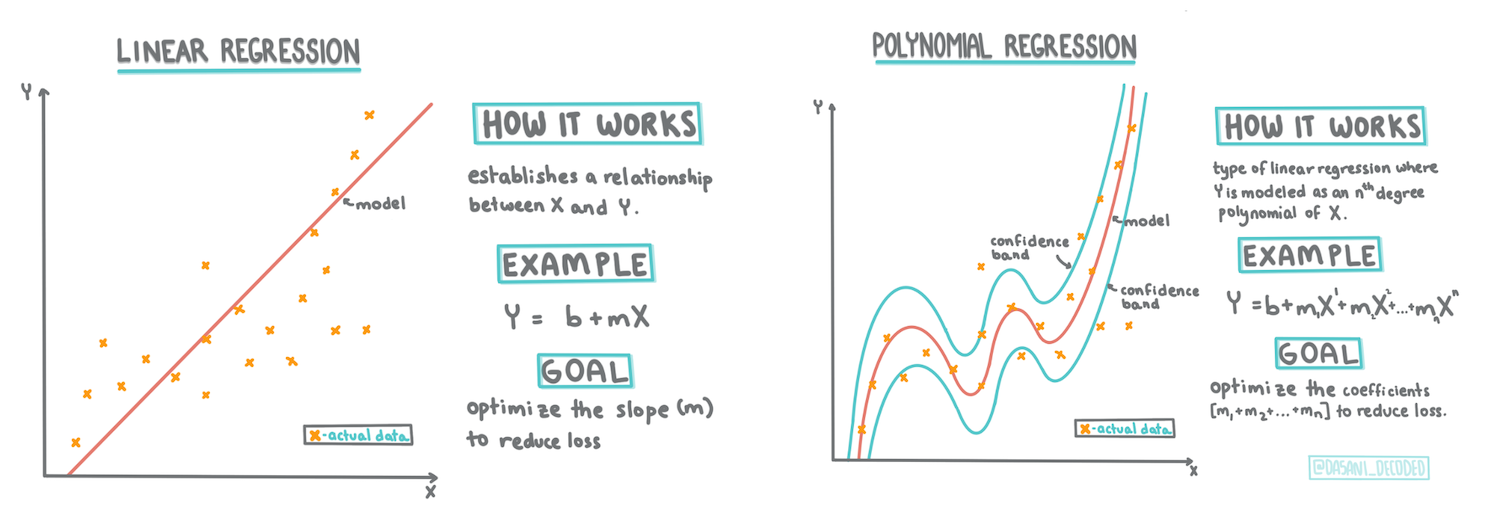
> Infografika avtorja [Dasani Madipalli](https://twitter.com/dasani_decoded)
## [Predavanje kviz](https://ff-quizzes.netlify.app/en/ml/)
> ### [To lekcijo lahko najdete tudi v jeziku R!](../../../../2-Regression/3-Linear/solution/R/lesson_3.html)
### Uvod
Do sedaj ste raziskali, kaj je regresija, z vzorčnimi podatki iz nabora podatkov o cenah buč, ki ga bomo uporabljali skozi celotno lekcijo. Prav tako ste podatke vizualizirali z uporabo knjižnice Matplotlib.
Zdaj ste pripravljeni, da se poglobite v regresijo za strojno učenje. Medtem ko vizualizacija omogoča razumevanje podatkov, je prava moč strojnega učenja v _treningu modelov_. Modele treniramo na zgodovinskih podatkih, da samodejno zajamejo odvisnosti podatkov, kar omogoča napovedovanje rezultatov za nove podatke, ki jih model še ni videl.
V tej lekciji boste izvedeli več o dveh vrstah regresije: _osnovni linearni regresiji_ in _polinomski regresiji_, skupaj z nekaj matematike, ki stoji za temi tehnikami. Ti modeli nam bodo omogočili napovedovanje cen buč glede na različne vhodne podatke.
[](https://youtu.be/CRxFT8oTDMg "ML za začetnike - Razumevanje linearne regresije")
> 🎥 Kliknite zgornjo sliko za kratek video pregled linearne regresije.
> Skozi celoten učni načrt predpostavljamo minimalno matematično predznanje in si prizadevamo, da bi bilo gradivo dostopno študentom iz drugih področij. Zato bodite pozorni na opombe, 🧮 poudarke, diagrame in druga učna orodja, ki pomagajo pri razumevanju.
### Predpogoji
Do zdaj bi morali biti že seznanjeni s strukturo podatkov o bučah, ki jih preučujemo. Najdete jih prednaložene in predhodno očiščene v datoteki _notebook.ipynb_ te lekcije. V datoteki so cene buč prikazane na bušel v novem podatkovnem okviru. Prepričajte se, da lahko zaženete te beležnice v jedrih Visual Studio Code.
### Priprava
Kot opomnik, te podatke nalagate, da bi si zastavili vprašanja, kot so:
- Kdaj je najboljši čas za nakup buč?
- Kakšno ceno lahko pričakujem za zabojček mini buč?
- Ali naj jih kupim v polovičnih bušelskih košarah ali v škatlah velikosti 1 1/9 bušla?
Poglobimo se v te podatke.
V prejšnji lekciji ste ustvarili podatkovni okvir Pandas in ga napolnili z delom izvirnega nabora podatkov, standardizirali cene na bušel. S tem pa ste lahko zbrali le približno 400 podatkovnih točk in le za jesenske mesece.
Oglejte si podatke, ki so prednaloženi v beležnici, ki spremlja to lekcijo. Podatki so prednaloženi, začetni raztrosni diagram pa je narisan, da prikaže podatke po mesecih. Morda lahko z dodatnim čiščenjem pridobimo več podrobnosti o naravi podatkov.
## Linearna regresijska premica
Kot ste se naučili v 1. lekciji, je cilj linearne regresije narisati premico, ki:
- **Prikaže odnose med spremenljivkami**. Prikaže razmerje med spremenljivkami.
- **Omogoča napovedi**. Omogoča natančne napovedi, kje bi nova podatkovna točka padla v razmerju do te premice.
Za risanje te vrste premice je značilna metoda **najmanjših kvadratov**. Izraz 'najmanjši kvadrati' pomeni, da so vse podatkovne točke okoli regresijske premice kvadrirane in nato seštejejo. Idealno je, da je ta končna vsota čim manjša, saj želimo nizko število napak ali `najmanjše kvadrate`.
To storimo, ker želimo modelirati premico, ki ima najmanjšo kumulativno razdaljo od vseh naših podatkovnih točk. Člene kvadriramo pred seštevanjem, saj nas zanima njihova velikost, ne pa smer.
> **🧮 Pokaži mi matematiko**
>
> Ta premica, imenovana _premica najboljše prileganja_, je izražena z [enačbo](https://en.wikipedia.org/wiki/Simple_linear_regression):
>
> ```
> Y = a + bX
> ```
>
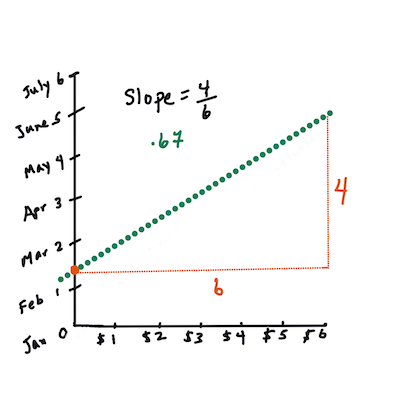
> `X` je 'pojasnjevalna spremenljivka'. `Y` je 'odvisna spremenljivka'. Naklon premice je `b`, `a` pa je presečišče z osjo y, kar se nanaša na vrednost `Y`, ko `X = 0`.
>
>
>
> Najprej izračunajte naklon `b`. Infografika avtorja [Jen Looper](https://twitter.com/jenlooper)
>
> Z drugimi besedami, glede na naše izvirno vprašanje o podatkih o bučah: "napovedati ceno buče na bušel glede na mesec", bi `X` predstavljal ceno, `Y` pa mesec prodaje.
>
>
>
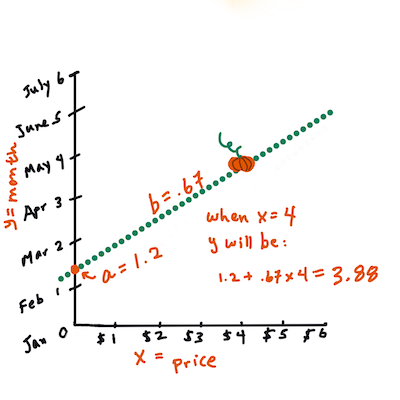
> Izračunajte vrednost Y. Če plačujete približno 4 $, mora biti april! Infografika avtorja [Jen Looper](https://twitter.com/jenlooper)
>
> Matematika, ki izračuna premico, mora prikazati njen naklon, ki je odvisen tudi od presečišča, torej od tega, kje se `Y` nahaja, ko `X = 0`.
>
> Metodo izračuna teh vrednosti si lahko ogledate na spletnem mestu [Math is Fun](https://www.mathsisfun.com/data/least-squares-regression.html). Obiščite tudi [ta kalkulator najmanjših kvadratov](https://www.mathsisfun.com/data/least-squares-calculator.html), da vidite, kako vrednosti številk vplivajo na premico.
## Korelacija
Še en izraz, ki ga je treba razumeti, je **koeficient korelacije** med danima spremenljivkama X in Y. Z raztrosnim diagramom lahko hitro vizualizirate ta koeficient. Diagram s podatkovnimi točkami, razporejenimi v ravni črti, ima visoko korelacijo, medtem ko ima diagram s podatkovnimi točkami, razpršenimi povsod med X in Y, nizko korelacijo.
Dober model linearne regresije bo tisti, ki ima visok (bližje 1 kot 0) koeficient korelacije z uporabo metode najmanjših kvadratov in regresijske premice.
✅ Zaženite beležnico, ki spremlja to lekcijo, in si oglejte raztrosni diagram meseca in cene. Ali se vam zdi, da imajo podatki, ki povezujejo mesec in ceno prodaje buč, visoko ali nizko korelacijo glede na vašo vizualno interpretacijo raztrosnega diagrama? Ali se to spremeni, če uporabite bolj natančno merilo namesto `Mesec`, npr. *dan v letu* (tj. število dni od začetka leta)?
V spodnji kodi bomo predpostavili, da smo očistili podatke in pridobili podatkovni okvir z imenom `new_pumpkins`, podoben naslednjemu:
ID | Mesec | DanVLeto | Vrsta | Mesto | Paket | Najnižja cena | Najvišja cena | Cena
---|-------|----------|-------|-------|-------|---------------|---------------|------
70 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 škatle | 15.0 | 15.0 | 13.636364
71 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 škatle | 18.0 | 18.0 | 16.363636
72 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 škatle | 18.0 | 18.0 | 16.363636
73 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 škatle | 17.0 | 17.0 | 15.454545
74 | 10 | 281 | PIE TYPE | BALTIMORE | 1 1/9 škatle | 15.0 | 15.0 | 13.636364
> Koda za čiščenje podatkov je na voljo v datoteki [`notebook.ipynb`](../../../../2-Regression/3-Linear/notebook.ipynb). Izvedli smo enake korake čiščenja kot v prejšnji lekciji in izračunali stolpec `DanVLeto` z naslednjim izrazom:
```python
day_of_year = pd.to_datetime(pumpkins['Date']).apply(lambda dt: (dt-datetime(dt.year,1,1)).days)
```
Zdaj, ko razumete matematiko za linearno regresijo, ustvarimo regresijski model, da preverimo, ali lahko napovemo, kateri paket buč bo imel najboljše cene. Nekdo, ki kupuje buče za praznični bučni nasad, bi morda želel te informacije, da bi optimiziral svoje nakupe paketov buč za nasad.
## Iskanje korelacije
[](https://youtu.be/uoRq-lW2eQo "ML za začetnike - Iskanje korelacije: Ključ do linearne regresije")
> 🎥 Kliknite zgornjo sliko za kratek video pregled korelacije.
Iz prejšnje lekcije ste verjetno videli, da povprečna cena za različne mesece izgleda takole:
To nakazuje, da bi morala obstajati neka korelacija, in lahko poskusimo trenirati linearni regresijski model za napovedovanje razmerja med `Mesec` in `Cena` ali med `DanVLeto` in `Cena`. Tukaj je raztrosni diagram, ki prikazuje slednje razmerje:
Preverimo, ali obstaja korelacija, z uporabo funkcije `corr`:
```python
print(new_pumpkins['Month'].corr(new_pumpkins['Price']))
print(new_pumpkins['DayOfYear'].corr(new_pumpkins['Price']))
```
Zdi se, da je korelacija precej majhna, -0,15 za `Mesec` in -0,17 za `DanVLeto`, vendar bi lahko obstajalo drugo pomembno razmerje. Zdi se, da obstajajo različni grozdi cen, ki ustrezajo različnim vrstam buč. Da potrdimo to hipotezo, narišimo vsako kategorijo buč z drugo barvo. S posredovanjem parametra `ax` funkciji za risanje raztrosa lahko narišemo vse točke na isti grafikon:
```python
ax=None
colors = ['red','blue','green','yellow']
for i,var in enumerate(new_pumpkins['Variety'].unique()):
df = new_pumpkins[new_pumpkins['Variety']==var]
ax = df.plot.scatter('DayOfYear','Price',ax=ax,c=colors[i],label=var)
```
Naša raziskava nakazuje, da ima vrsta buče večji vpliv na skupno ceno kot dejanski datum prodaje. To lahko vidimo z barvnim grafom:
```python
new_pumpkins.groupby('Variety')['Price'].mean().plot(kind='bar')
```
Osredotočimo se za trenutek samo na eno vrsto buč, 'pie type', in preverimo, kakšen vpliv ima datum na ceno:
```python
pie_pumpkins = new_pumpkins[new_pumpkins['Variety']=='PIE TYPE']
pie_pumpkins.plot.scatter('DayOfYear','Price')
```
Če zdaj izračunamo korelacijo med `Cena` in `DanVLeto` z uporabo funkcije `corr`, bomo dobili nekaj okoli `-0,27` - kar pomeni, da ima smisel trenirati napovedni model.
> Pred treningom linearnega regresijskega modela je pomembno zagotoviti, da so naši podatki čisti. Linearna regresija ne deluje dobro z manjkajočimi vrednostmi, zato je smiselno odstraniti vse prazne celice:
```python
pie_pumpkins.dropna(inplace=True)
pie_pumpkins.info()
```
Drugi pristop bi bil zapolniti te prazne vrednosti s povprečnimi vrednostmi iz ustreznega stolpca.
## Enostavna linearna regresija
[](https://youtu.be/e4c_UP2fSjg "ML za začetnike - Linearna in polinomska regresija z uporabo Scikit-learn")
> 🎥 Kliknite zgornjo sliko za kratek video pregled linearne in polinomske regresije.
Za treniranje našega linearnega regresijskega modela bomo uporabili knjižnico **Scikit-learn**.
```python
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
```
Začnemo z ločevanjem vhodnih vrednosti (značilnosti) in pričakovanega izhoda (oznake) v ločena numpy polja:
```python
X = pie_pumpkins['DayOfYear'].to_numpy().reshape(-1,1)
y = pie_pumpkins['Price']
```
> Upoštevajte, da smo morali izvesti `reshape` na vhodnih podatkih, da jih Linear Regression paket pravilno razume. Linearna regresija pričakuje 2D polje kot vhod, kjer vsaka vrstica polja ustreza vektorju vhodnih značilnosti. V našem primeru, ker imamo samo en vhod, potrebujemo polje oblike N×1, kjer je N velikost nabora podatkov.
Nato moramo podatke razdeliti na učni in testni nabor, da lahko po treningu preverimo naš model:
```python
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
```
Na koncu trening dejanskega linearnega regresijskega modela zahteva le dve vrstici kode. Definiramo objekt `LinearRegression` in ga prilagodimo našim podatkom z uporabo metode `fit`:
```python
lin_reg = LinearRegression()
lin_reg.fit(X_train,y_train)
```
Objekt `LinearRegression` po prilagoditvi vsebuje vse koeficiente regresije, do katerih lahko dostopamo z lastnostjo `.coef_`. V našem primeru je le en koeficient, ki bi moral biti okoli `-0,017`. To pomeni, da se cene zdi, da rahlo padajo s časom, vendar ne preveč, približno 2 centa na dan. Prav tako lahko dostopamo do presečišča regresije z osjo Y z uporabo `lin_reg.intercept_` - v našem primeru bo to okoli `21`, kar kaže na ceno na začetku leta.
Da vidimo, kako natančen je naš model, lahko napovemo cene na testnem naboru podatkov in nato izmerimo, kako blizu so naše napovedi pričakovanim vrednostim. To lahko storimo z uporabo metrike srednje kvadratne napake (MSE), ki je povprečje vseh kvadratnih razlik med pričakovano in napovedano vrednostjo.
```python
pred = lin_reg.predict(X_test)
mse = np.sqrt(mean_squared_error(y_test,pred))
print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)')
```
Naša napaka se zdi okoli 2 točk, kar je približno 17 %. Ni ravno dobro. Drug kazalnik kakovosti modela je **koeficient determinacije**, ki ga lahko pridobimo na naslednji način:
```python
score = lin_reg.score(X_train,y_train)
print('Model determination: ', score)
```
Če je vrednost 0, to pomeni, da model ne upošteva vhodnih podatkov in deluje kot *najslabši linearni napovedovalec*, kar je preprosto povprečna vrednost rezultata. Vrednost 1 pomeni, da lahko popolnoma napovemo vse pričakovane izhode. V našem primeru je koeficient okoli 0,06, kar je precej nizko.
Prav tako lahko narišemo testne podatke skupaj z regresijsko premico, da bolje vidimo, kako regresija deluje v našem primeru:
```python
plt.scatter(X_test,y_test)
plt.plot(X_test,pred)
```
## Polinomska regresija
Druga vrsta linearne regresije je polinomska regresija. Čeprav včasih obstaja linearna povezava med spremenljivkami – večja kot je buča po prostornini, višja je cena – včasih teh povezav ni mogoče prikazati kot ravnino ali premico.
✅ Tukaj so [nekateri dodatni primeri](https://online.stat.psu.edu/stat501/lesson/9/9.8) podatkov, ki bi lahko uporabili polinomsko regresijo.
Poglejte še enkrat razmerje med datumom in ceno. Ali se zdi, da bi moral biti ta raztros nujno analiziran s premico? Ali cene ne morejo nihati? V tem primeru lahko poskusite polinomsko regresijo.
✅ Polinomi so matematični izrazi, ki lahko vsebujejo eno ali več spremenljivk in koeficientov.
Polinomska regresija ustvari ukrivljeno premico, ki bolje ustreza nelinearnim podatkom. V našem primeru, če v vhodne podatke vključimo kvadratno spremenljivko `DayOfYear`, bi morali biti sposobni prilagoditi naše podatke s parabolično krivuljo, ki bo imela minimum na določenem mestu v letu.
Scikit-learn vključuje uporabno [API za pipeline](https://scikit-learn.org/stable/modules/generated/sklearn.pipeline.make_pipeline.html?highlight=pipeline#sklearn.pipeline.make_pipeline), ki združuje različne korake obdelave podatkov. **Pipeline** je veriga **ocenjevalcev**. V našem primeru bomo ustvarili pipeline, ki najprej doda polinomske značilnosti našemu modelu, nato pa izvede regresijo:
```python
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression())
pipeline.fit(X_train,y_train)
```
Uporaba `PolynomialFeatures(2)` pomeni, da bomo vključili vse polinome druge stopnje iz vhodnih podatkov. V našem primeru to pomeni le `DayOfYear`2, vendar ob dveh vhodnih spremenljivkah X in Y to doda X2, XY in Y2. Uporabimo lahko tudi polinome višjih stopenj, če želimo.
Pipeline lahko uporabljamo na enak način kot originalni objekt `LinearRegression`, tj. lahko uporabimo `fit` za prilagoditev modela in nato `predict` za pridobitev rezultatov napovedi. Tukaj je graf, ki prikazuje testne podatke in aproksimacijsko krivuljo:
S polinomsko regresijo lahko dosežemo nekoliko nižji MSE in višji koeficient determinacije, vendar ne bistveno. Upoštevati moramo tudi druge značilnosti!
> Opazite, da so najnižje cene buč opazovane nekje okoli noči čarovnic. Kako to razložite?
🎃 Čestitke, pravkar ste ustvarili model, ki lahko pomaga napovedati ceno buč za pite. Verjetno lahko ponovite isti postopek za vse vrste buč, vendar bi bilo to zamudno. Zdaj se naučimo, kako upoštevati različne vrste buč v našem modelu!
## Kategorijske značilnosti
V idealnem svetu bi želeli napovedati cene za različne vrste buč z istim modelom. Vendar je stolpec `Variety` nekoliko drugačen od stolpcev, kot je `Month`, saj vsebuje nenumerične vrednosti. Takšni stolpci se imenujejo **kategorijski**.
[](https://youtu.be/DYGliioIAE0 "ML za začetnike - Napovedovanje kategorijskih značilnosti z linearno regresijo")
> 🎥 Kliknite zgornjo sliko za kratek video pregled uporabe kategorijskih značilnosti.
Tukaj lahko vidite, kako povprečna cena odvisna od vrste buče:
Da upoštevamo vrsto buče, jo moramo najprej pretvoriti v numerično obliko, ali jo **kodirati**. Obstaja več načinov, kako to storiti:
* Preprosto **numerično kodiranje** bo ustvarilo tabelo različnih vrst in nato zamenjalo ime vrste z indeksom v tej tabeli. To ni najboljša ideja za linearno regresijo, saj linearna regresija upošteva dejansko numerično vrednost indeksa in jo doda rezultatu, pomnoženo z nekim koeficientom. V našem primeru je razmerje med številko indeksa in ceno očitno nelinearno, tudi če poskrbimo, da so indeksi urejeni na določen način.
* **One-hot kodiranje** bo zamenjalo stolpec `Variety` s 4 različnimi stolpci, enim za vsako vrsto. Vsak stolpec bo vseboval `1`, če je ustrezna vrstica določene vrste, in `0` sicer. To pomeni, da bo v linearni regresiji štiri koeficiente, po enega za vsako vrsto buče, ki bodo odgovorni za "začetno ceno" (ali bolje "dodatno ceno") za to določeno vrsto.
Spodnja koda prikazuje, kako lahko izvedemo one-hot kodiranje vrste:
```python
pd.get_dummies(new_pumpkins['Variety'])
```
ID | FAIRYTALE | MINIATURE | MIXED HEIRLOOM VARIETIES | PIE TYPE
----|-----------|-----------|--------------------------|----------
70 | 0 | 0 | 0 | 1
71 | 0 | 0 | 0 | 1
... | ... | ... | ... | ...
1738 | 0 | 1 | 0 | 0
1739 | 0 | 1 | 0 | 0
1740 | 0 | 1 | 0 | 0
1741 | 0 | 1 | 0 | 0
1742 | 0 | 1 | 0 | 0
Za treniranje linearne regresije z uporabo one-hot kodirane vrste kot vhodnih podatkov moramo le pravilno inicializirati podatke `X` in `y`:
```python
X = pd.get_dummies(new_pumpkins['Variety'])
y = new_pumpkins['Price']
```
Preostala koda je enaka kot tista, ki smo jo uporabili zgoraj za treniranje linearne regresije. Če jo preizkusite, boste videli, da je povprečna kvadratna napaka približno enaka, vendar dobimo veliko višji koeficient determinacije (~77 %). Za še bolj natančne napovedi lahko upoštevamo več kategorijskih značilnosti, pa tudi numerične značilnosti, kot sta `Month` ali `DayOfYear`. Za pridobitev ene velike matrike značilnosti lahko uporabimo `join`:
```python
X = pd.get_dummies(new_pumpkins['Variety']) \
.join(new_pumpkins['Month']) \
.join(pd.get_dummies(new_pumpkins['City'])) \
.join(pd.get_dummies(new_pumpkins['Package']))
y = new_pumpkins['Price']
```
Tukaj upoštevamo tudi `City` in vrsto `Package`, kar nam daje MSE 2,84 (10 %) in determinacijo 0,94!
## Vse skupaj
Za najboljši model lahko uporabimo kombinirane (one-hot kodirane kategorijske + numerične) podatke iz zgornjega primera skupaj s polinomsko regresijo. Tukaj je celotna koda za vašo uporabo:
```python
# set up training data
X = pd.get_dummies(new_pumpkins['Variety']) \
.join(new_pumpkins['Month']) \
.join(pd.get_dummies(new_pumpkins['City'])) \
.join(pd.get_dummies(new_pumpkins['Package']))
y = new_pumpkins['Price']
# make train-test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# setup and train the pipeline
pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression())
pipeline.fit(X_train,y_train)
# predict results for test data
pred = pipeline.predict(X_test)
# calculate MSE and determination
mse = np.sqrt(mean_squared_error(y_test,pred))
print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)')
score = pipeline.score(X_train,y_train)
print('Model determination: ', score)
```
To bi nam moralo dati najboljši koeficient determinacije skoraj 97 % in MSE=2,23 (~8 % napake pri napovedi).
| Model | MSE | Determinacija |
|-------|-----|---------------|
| `DayOfYear` Linear | 2,77 (17,2 %) | 0,07 |
| `DayOfYear` Polinomski | 2,73 (17,0 %) | 0,08 |
| `Variety` Linear | 5,24 (19,7 %) | 0,77 |
| Vse značilnosti Linear | 2,84 (10,5 %) | 0,94 |
| Vse značilnosti Polinomski | 2,23 (8,25 %) | 0,97 |
🏆 Odlično! Ustvarili ste štiri regresijske modele v eni lekciji in izboljšali kakovost modela na 97 %. V zadnjem delu o regresiji se boste naučili o logistični regresiji za določanje kategorij.
---
## 🚀Izziv
Preizkusite več različnih spremenljivk v tej beležnici, da vidite, kako korelacija ustreza natančnosti modela.
## [Kvizi po predavanju](https://ff-quizzes.netlify.app/en/ml/)
## Pregled in samostojno učenje
V tej lekciji smo se naučili o linearni regresiji. Obstajajo tudi druge pomembne vrste regresije. Preberite o tehnikah Stepwise, Ridge, Lasso in Elasticnet. Dober tečaj za nadaljnje učenje je [Stanfordov tečaj statističnega učenja](https://online.stanford.edu/courses/sohs-ystatslearning-statistical-learning).
## Naloga
[Ustvarite model](assignment.md)
---
**Omejitev odgovornosti**:
Ta dokument je bil preveden z uporabo storitve za strojno prevajanje [Co-op Translator](https://github.com/Azure/co-op-translator). Čeprav si prizadevamo za natančnost, vas prosimo, da upoštevate, da lahko avtomatizirani prevodi vsebujejo napake ali netočnosti. Izvirni dokument v njegovem izvirnem jeziku je treba obravnavati kot avtoritativni vir. Za ključne informacije priporočamo strokovno človeško prevajanje. Ne prevzemamo odgovornosti za morebitna nesporazumevanja ali napačne razlage, ki izhajajo iz uporabe tega prevoda.