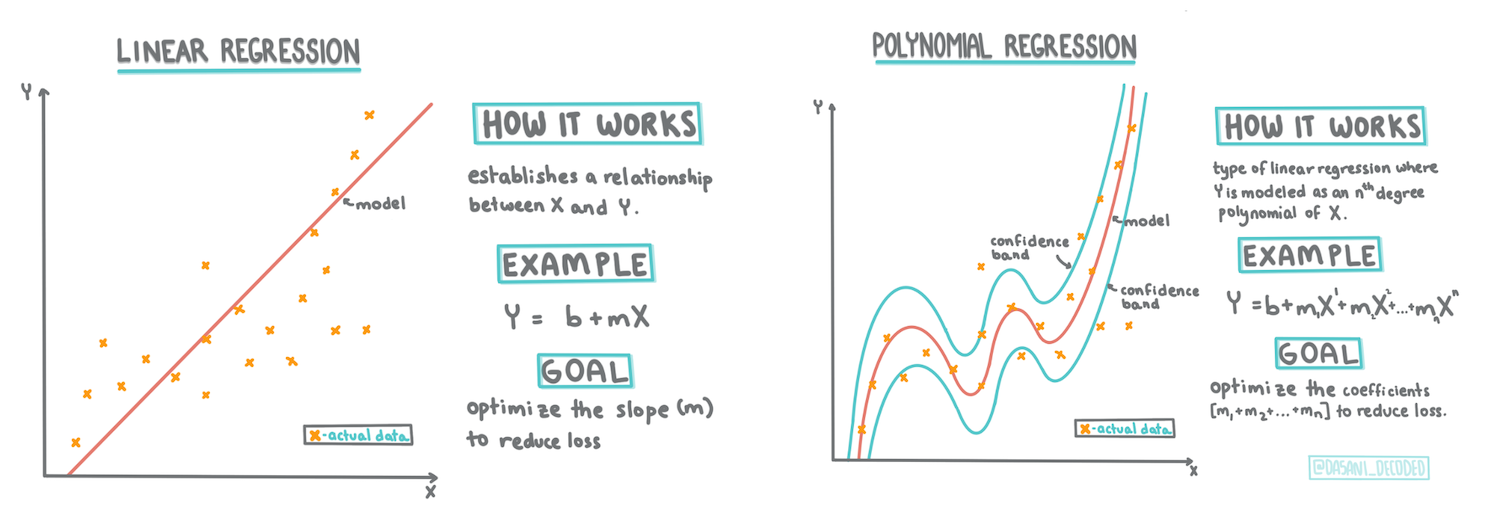
# Построение модели регрессии с использованием Scikit-learn: четыре способа регрессии  > Инфографика от [Dasani Madipalli](https://twitter.com/dasani_decoded) ## [Тест перед лекцией](https://ff-quizzes.netlify.app/en/ml/) > ### [Этот урок доступен на R!](../../../../2-Regression/3-Linear/solution/R/lesson_3.html) ### Введение До этого момента вы изучали, что такое регрессия, используя пример данных из набора данных о ценах на тыквы, который мы будем использовать на протяжении всего урока. Вы также визуализировали данные с помощью Matplotlib. Теперь вы готовы углубиться в регрессию для машинного обучения. Визуализация помогает понять данные, но настоящая сила машинного обучения заключается в _обучении моделей_. Модели обучаются на исторических данных, чтобы автоматически выявлять зависимости в данных, и позволяют предсказывать результаты для новых данных, которые модель ранее не видела. В этом уроке вы узнаете больше о двух типах регрессии: _основной линейной регрессии_ и _полиномиальной регрессии_, а также о некоторых математических основах этих методов. Эти модели позволят нам предсказывать цены на тыквы в зависимости от различных входных данных. [](https://youtu.be/CRxFT8oTDMg "Машинное обучение для начинающих - Понимание линейной регрессии") > 🎥 Нажмите на изображение выше, чтобы посмотреть короткий видеообзор линейной регрессии. > В рамках этой программы мы предполагаем минимальные знания математики и стремимся сделать материал доступным для студентов из других областей. Следите за заметками, 🧮 подсказками, диаграммами и другими инструментами обучения, которые помогут вам понять материал. ### Предварительные знания На данный момент вы должны быть знакомы со структурой данных о тыквах, которые мы изучаем. Вы можете найти их предварительно загруженными и очищенными в файле _notebook.ipynb_ этого урока. В файле цена на тыквы отображается за бушель в новом датафрейме. Убедитесь, что вы можете запускать эти ноутбуки в ядрах Visual Studio Code. ### Подготовка Напомним, что вы загружаете эти данные, чтобы задавать им вопросы. - Когда лучше всего покупать тыквы? - Какую цену можно ожидать за коробку миниатюрных тыкв? - Стоит ли покупать их в корзинах на полбушеля или в коробках на 1 1/9 бушеля? Давайте продолжим изучение этих данных. В предыдущем уроке вы создали датафрейм Pandas и заполнили его частью исходного набора данных, стандартизировав цены по бушелю. Однако, сделав это, вы смогли собрать только около 400 точек данных, и только за осенние месяцы. Посмотрите на данные, которые предварительно загружены в ноутбуке, сопровождающем этот урок. Данные предварительно загружены, и начальный диаграмма рассеяния построена, чтобы показать данные по месяцам. Возможно, мы сможем получить немного больше информации о природе данных, если очистим их более тщательно. ## Линия линейной регрессии Как вы узнали в Уроке 1, цель упражнения по линейной регрессии — построить линию, чтобы: - **Показать взаимосвязь переменных**. Показать связь между переменными. - **Сделать прогнозы**. Сделать точные прогнозы о том, где новая точка данных окажется относительно этой линии. Обычно для построения такой линии используется метод **наименьших квадратов**. Термин "наименьшие квадраты" означает, что все точки данных вокруг линии регрессии возводятся в квадрат, а затем складываются. В идеале, итоговая сумма должна быть как можно меньше, так как мы хотим минимизировать количество ошибок, или `наименьшие квадраты`. Мы делаем это, потому что хотим смоделировать линию, которая имеет наименьшее суммарное расстояние от всех наших точек данных. Мы также возводим термины в квадрат перед их сложением, так как нас интересует их величина, а не направление. 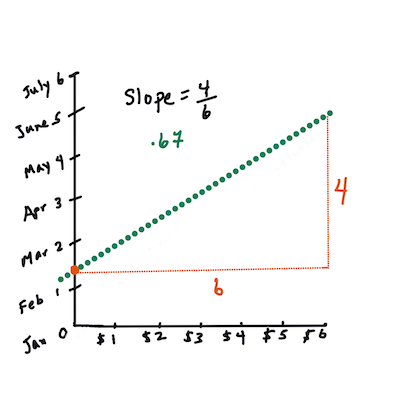> **🧮 Покажите мне математику** > > Эта линия, называемая _линией наилучшего соответствия_, может быть выражена [уравнением](https://en.wikipedia.org/wiki/Simple_linear_regression): > > ``` > Y = a + bX > ``` > > `X` — это "объясняющая переменная". `Y` — это "зависимая переменная". Наклон линии — это `b`, а `a` — это пересечение с осью Y, которое относится к значению `Y`, когда `X = 0`. > > > > Сначала вычислите наклон `b`. 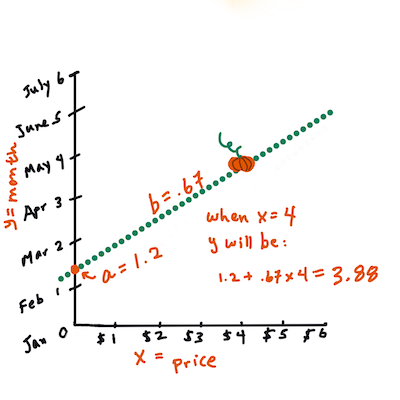Инфографика от [Jen Looper](https://twitter.com/jenlooper) > > Другими словами, если обратиться к исходному вопросу о данных о тыквах: "предсказать цену тыквы за бушель по месяцам", `X` будет относиться к цене, а `Y` — к месяцу продажи. > > > > Вычислите значение Y. Если вы платите около $4, значит, это апрель! Инфографика от [Jen Looper](https://twitter.com/jenlooper) > > Математика, которая вычисляет линию, должна демонстрировать наклон линии, который также зависит от пересечения, или от того, где `Y` находится, когда `X = 0`. > > Вы можете ознакомиться с методом вычисления этих значений на сайте [Math is Fun](https://www.mathsisfun.com/data/least-squares-regression.html). Также посетите [этот калькулятор наименьших квадратов](https://www.mathsisfun.com/data/least-squares-calculator.html), чтобы увидеть, как значения чисел влияют на линию. ## Корреляция Еще один термин, который важно понять, — это **коэффициент корреляции** между заданными переменными X и Y. Используя диаграмму рассеяния, вы можете быстро визуализировать этот коэффициент. Диаграмма с точками данных, расположенными в аккуратной линии, имеет высокую корреляцию, а диаграмма с точками данных, разбросанными повсюду между X и Y, имеет низкую корреляцию. Хорошая модель линейной регрессии будет той, которая имеет высокий коэффициент корреляции (ближе к 1, чем к 0) при использовании метода наименьших квадратов с линией регрессии. ✅ Запустите ноутбук, сопровождающий этот урок, и посмотрите на диаграмму рассеяния "Месяц к цене". Кажется ли, что данные, связывающие месяц с ценой продаж тыкв, имеют высокую или низкую корреляцию, согласно вашему визуальному восприятию диаграммы рассеяния? Изменится ли это, если использовать более точную меру вместо `Месяц`, например, *день года* (т.е. количество дней с начала года)? В приведенном ниже коде мы предполагаем, что мы очистили данные и получили датафрейм под названием `new_pumpkins`, похожий на следующий: ID | Месяц | ДеньГода | Сорт | Город | Упаковка | Низкая цена | Высокая цена | Цена ---|-------|----------|------|-------|----------|-------------|--------------|----- 70 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 15.0 | 15.0 | 13.636364 71 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 18.0 | 18.0 | 16.363636 72 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 18.0 | 18.0 | 16.363636 73 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 17.0 | 17.0 | 15.454545 74 | 10 | 281 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 15.0 | 15.0 | 13.636364 > Код для очистки данных доступен в [`notebook.ipynb`](../../../../2-Regression/3-Linear/notebook.ipynb). Мы выполнили те же шаги очистки, что и в предыдущем уроке, и вычислили столбец `DayOfYear` с использованием следующего выражения: ```python day_of_year = pd.to_datetime(pumpkins['Date']).apply(lambda dt: (dt-datetime(dt.year,1,1)).days) ``` Теперь, когда вы понимаете математику линейной регрессии, давайте создадим модель регрессии, чтобы выяснить, какой пакет тыкв будет иметь лучшие цены на тыквы. Кто-то, покупающий тыквы для праздничного тыквенного поля, может захотеть получить эту информацию, чтобы оптимизировать свои покупки пакетов тыкв для поля. ## Поиск корреляции [](https://youtu.be/uoRq-lW2eQo "Машинное обучение для начинающих - Поиск корреляции: ключ к линейной регрессии") > 🎥 Нажмите на изображение выше, чтобы посмотреть короткий видеообзор корреляции. Из предыдущего урока вы, вероятно, видели, что средняя цена за разные месяцы выглядит следующим образом: Это предполагает, что должна быть некоторая корреляция, и мы можем попробовать обучить модель линейной регрессии, чтобы предсказать связь между `Месяцем` и `Ценой`, или между `ДнемГода` и `Ценой`. Вот диаграмма рассеяния, показывающая последнюю связь: Давайте проверим наличие корреляции с помощью функции `corr`: ```python print(new_pumpkins['Month'].corr(new_pumpkins['Price'])) print(new_pumpkins['DayOfYear'].corr(new_pumpkins['Price'])) ``` Кажется, что корреляция довольно мала, -0.15 для `Месяца` и -0.17 для `ДняГода`, но может быть другая важная связь. Похоже, что существуют разные кластеры цен, соответствующие различным сортам тыкв. Чтобы подтвердить эту гипотезу, давайте построим график, где каждая категория тыкв будет отображаться разным цветом. Передавая параметр `ax` в функцию построения диаграммы рассеяния, мы можем построить все точки на одном графике: ```python ax=None colors = ['red','blue','green','yellow'] for i,var in enumerate(new_pumpkins['Variety'].unique()): df = new_pumpkins[new_pumpkins['Variety']==var] ax = df.plot.scatter('DayOfYear','Price',ax=ax,c=colors[i],label=var) ``` Наше исследование предполагает, что сорт тыкв оказывает большее влияние на общую цену, чем фактическая дата продажи. Мы можем увидеть это на столбчатом графике: ```python new_pumpkins.groupby('Variety')['Price'].mean().plot(kind='bar') ``` Давайте сосредоточимся на одном сорте тыкв, 'pie type', и посмотрим, какое влияние дата оказывает на цену: ```python pie_pumpkins = new_pumpkins[new_pumpkins['Variety']=='PIE TYPE'] pie_pumpkins.plot.scatter('DayOfYear','Price') ``` Если теперь рассчитать корреляцию между `Ценой` и `ДнемГода` с помощью функции `corr`, мы получим что-то около `-0.27`, что означает, что обучение предсказательной модели имеет смысл. > Перед обучением модели линейной регрессии важно убедиться, что наши данные чистые. Линейная регрессия плохо работает с пропущенными значениями, поэтому имеет смысл избавиться от всех пустых ячеек: ```python pie_pumpkins.dropna(inplace=True) pie_pumpkins.info() ``` Другой подход — заполнить эти пустые значения средними значениями из соответствующего столбца. ## Простая линейная регрессия [](https://youtu.be/e4c_UP2fSjg "Машинное обучение для начинающих - Линейная и полиномиальная регрессия с использованием Scikit-learn") > 🎥 Нажмите на изображение выше, чтобы посмотреть короткий видеообзор линейной и полиномиальной регрессии. Для обучения нашей модели линейной регрессии мы будем использовать библиотеку **Scikit-learn**. ```python from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error from sklearn.model_selection import train_test_split ``` Начнем с разделения входных значений (признаков) и ожидаемого результата (метки) на отдельные массивы numpy: ```python X = pie_pumpkins['DayOfYear'].to_numpy().reshape(-1,1) y = pie_pumpkins['Price'] ``` > Обратите внимание, что нам пришлось выполнить `reshape` для входных данных, чтобы пакет линейной регрессии понял их правильно. Линейная регрессия ожидает 2D-массив в качестве входных данных, где каждая строка массива соответствует вектору входных признаков. В нашем случае, поскольку у нас есть только один вход, нам нужен массив с формой N×1, где N — размер набора данных. Затем нам нужно разделить данные на обучающий и тестовый наборы, чтобы мы могли проверить нашу модель после обучения: ```python X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) ``` Наконец, обучение самой модели линейной регрессии занимает всего две строки кода. Мы определяем объект `LinearRegression` и обучаем его на наших данных с помощью метода `fit`: ```python lin_reg = LinearRegression() lin_reg.fit(X_train,y_train) ``` Объект `LinearRegression` после выполнения метода `fit` содержит все коэффициенты регрессии, которые можно получить с помощью свойства `.coef_`. В нашем случае есть только один коэффициент, который должен быть около `-0.017`. Это означает, что цены, кажется, немного снижаются со временем, но не слишком сильно, примерно на 2 цента в день. Мы также можем получить точку пересечения регрессии с осью Y, используя `lin_reg.intercept_` — она будет около `21` в нашем случае, что указывает на цену в начале года. Чтобы увидеть, насколько точна наша модель, мы можем предсказать цены на тестовом наборе данных, а затем измерить, насколько близки наши прогнозы к ожидаемым значениям. Это можно сделать с помощью метрики среднеквадратичной ошибки (MSE), которая представляет собой среднее всех квадратов разностей между ожидаемым и предсказанным значением. ```python pred = lin_reg.predict(X_test) mse = np.sqrt(mean_squared_error(y_test,pred)) print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)') ``` Наша ошибка составляет около 2 пунктов, что примерно 17%. Не слишком хорошо. Еще один показатель качества модели — **коэффициент детерминации**, который можно получить следующим образом: ```python score = lin_reg.score(X_train,y_train) print('Model determination: ', score) ``` Если значение равно 0, это означает, что модель не учитывает входные данные и действует как *худший линейный предсказатель*, который просто является средним значением результата. Значение 1 означает, что мы можем идеально предсказать все ожидаемые выходные данные. В нашем случае коэффициент составляет около 0.06, что довольно низко. Мы также можем построить график тестовых данных вместе с линией регрессии, чтобы лучше понять, как работает регрессия в нашем случае: ```python plt.scatter(X_test,y_test) plt.plot(X_test,pred) ``` ## Полиномиальная регрессия Другой тип линейной регрессии — это полиномиальная регрессия. Хотя иногда между переменными существует линейная зависимость — например, чем больше объем тыквы, тем выше цена — иногда эти зависимости нельзя изобразить в виде плоскости или прямой линии. ✅ Вот [несколько примеров](https://online.stat.psu.edu/stat501/lesson/9/9.8) данных, которые могут использовать полиномиальную регрессию. Посмотрите еще раз на зависимость между датой и ценой. Кажется ли, что этот график обязательно должен быть проанализирован прямой линией? Разве цены не могут колебаться? В этом случае можно попробовать полиномиальную регрессию. ✅ Полиномы — это математические выражения, которые могут состоять из одной или нескольких переменных и коэффициентов. Полиномиальная регрессия создает кривую линию, чтобы лучше соответствовать нелинейным данным. В нашем случае, если мы включим квадратную переменную `DayOfYear` во входные данные, мы сможем подогнать наши данные под параболическую кривую, которая будет иметь минимум в определенный момент года. Scikit-learn включает удобный [API для создания конвейеров](https://scikit-learn.org/stable/modules/generated/sklearn.pipeline.make_pipeline.html?highlight=pipeline#sklearn.pipeline.make_pipeline), чтобы объединить различные этапы обработки данных. **Конвейер** — это цепочка **оценщиков**. В нашем случае мы создадим конвейер, который сначала добавит полиномиальные признаки в нашу модель, а затем обучит регрессию: ```python from sklearn.preprocessing import PolynomialFeatures from sklearn.pipeline import make_pipeline pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression()) pipeline.fit(X_train,y_train) ``` Использование `PolynomialFeatures(2)` означает, что мы включим все полиномы второй степени из входных данных. В нашем случае это просто будет `DayOfYear`², но если есть две входные переменные X и Y, это добавит X², XY и Y². Мы также можем использовать полиномы более высокой степени, если захотим. Конвейеры можно использовать так же, как и оригинальный объект `LinearRegression`, то есть мы можем выполнить `fit` для конвейера, а затем использовать `predict`, чтобы получить результаты предсказания. Вот график, показывающий тестовые данные и аппроксимационную кривую: Используя полиномиальную регрессию, мы можем получить немного более низкий MSE и более высокий коэффициент детерминации, но не значительно. Нам нужно учитывать другие признаки! > Вы можете заметить, что минимальные цены на тыквы наблюдаются примерно в период Хэллоуина. Как вы можете это объяснить? 🎃 Поздравляем, вы только что создали модель, которая может помочь предсказывать цену тыкв для пирогов. Вы, вероятно, можете повторить ту же процедуру для всех типов тыкв, но это было бы утомительно. Давайте теперь узнаем, как учитывать разновидности тыкв в нашей модели! ## Категориальные признаки В идеальном мире мы хотим иметь возможность предсказывать цены для разных разновидностей тыкв, используя одну и ту же модель. Однако столбец `Variety` несколько отличается от таких столбцов, как `Month`, потому что он содержит нечисловые значения. Такие столбцы называются **категориальными**. [](https://youtu.be/DYGliioIAE0 "ML для начинающих — предсказания с категориальными признаками в линейной регрессии") > 🎥 Нажмите на изображение выше, чтобы посмотреть короткий видеообзор использования категориальных признаков. Здесь вы можете увидеть, как средняя цена зависит от разновидности: Чтобы учитывать разновидность, сначала нужно преобразовать ее в числовую форму, или **закодировать**. Существует несколько способов сделать это: * Простое **числовое кодирование** создаст таблицу различных разновидностей, а затем заменит название разновидности индексом в этой таблице. Это не лучший вариант для линейной регрессии, потому что линейная регрессия учитывает фактическое числовое значение индекса и добавляет его к результату, умножая на некоторый коэффициент. В нашем случае связь между номером индекса и ценой явно нелинейна, даже если мы убедимся, что индексы упорядочены каким-то определенным образом. * **One-hot кодирование** заменит столбец `Variety` на 4 разных столбца, по одному для каждой разновидности. Каждый столбец будет содержать `1`, если соответствующая строка относится к данной разновидности, и `0` в противном случае. Это означает, что в линейной регрессии будет четыре коэффициента, по одному для каждой разновидности тыкв, отвечающих за "начальную цену" (или скорее "дополнительную цену") для этой конкретной разновидности. Код ниже показывает, как можно выполнить one-hot кодирование для разновидности: ```python pd.get_dummies(new_pumpkins['Variety']) ``` ID | FAIRYTALE | MINIATURE | MIXED HEIRLOOM VARIETIES | PIE TYPE ----|-----------|-----------|--------------------------|---------- 70 | 0 | 0 | 0 | 1 71 | 0 | 0 | 0 | 1 ... | ... | ... | ... | ... 1738 | 0 | 1 | 0 | 0 1739 | 0 | 1 | 0 | 0 1740 | 0 | 1 | 0 | 0 1741 | 0 | 1 | 0 | 0 1742 | 0 | 1 | 0 | 0 Чтобы обучить линейную регрессию, используя one-hot кодированную разновидность в качестве входных данных, нам просто нужно правильно инициализировать данные `X` и `y`: ```python X = pd.get_dummies(new_pumpkins['Variety']) y = new_pumpkins['Price'] ``` Остальной код такой же, как тот, который мы использовали выше для обучения линейной регрессии. Если вы попробуете его, то увидите, что среднеквадратичная ошибка примерно такая же, но мы получаем гораздо более высокий коэффициент детерминации (~77%). Чтобы получить еще более точные предсказания, мы можем учитывать больше категориальных признаков, а также числовые признаки, такие как `Month` или `DayOfYear`. Чтобы получить один большой массив признаков, мы можем использовать `join`: ```python X = pd.get_dummies(new_pumpkins['Variety']) \ .join(new_pumpkins['Month']) \ .join(pd.get_dummies(new_pumpkins['City'])) \ .join(pd.get_dummies(new_pumpkins['Package'])) y = new_pumpkins['Price'] ``` Здесь мы также учитываем `City` и тип упаковки `Package`, что дает нам MSE 2.84 (10%) и коэффициент детерминации 0.94! ## Собираем все вместе Чтобы создать лучшую модель, мы можем использовать комбинированные данные (one-hot кодированные категориальные + числовые) из примера выше вместе с полиномиальной регрессией. Вот полный код для вашего удобства: ```python # set up training data X = pd.get_dummies(new_pumpkins['Variety']) \ .join(new_pumpkins['Month']) \ .join(pd.get_dummies(new_pumpkins['City'])) \ .join(pd.get_dummies(new_pumpkins['Package'])) y = new_pumpkins['Price'] # make train-test split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) # setup and train the pipeline pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression()) pipeline.fit(X_train,y_train) # predict results for test data pred = pipeline.predict(X_test) # calculate MSE and determination mse = np.sqrt(mean_squared_error(y_test,pred)) print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)') score = pipeline.score(X_train,y_train) print('Model determination: ', score) ``` Это должно дать нам лучший коэффициент детерминации почти 97% и MSE=2.23 (~8% ошибки предсказания). | Модель | MSE | Коэффициент детерминации | |--------|-----|--------------------------| | `DayOfYear` Линейная | 2.77 (17.2%) | 0.07 | | `DayOfYear` Полиномиальная | 2.73 (17.0%) | 0.08 | | `Variety` Линейная | 5.24 (19.7%) | 0.77 | | Все признаки Линейная | 2.84 (10.5%) | 0.94 | | Все признаки Полиномиальная | 2.23 (8.25%) | 0.97 | 🏆 Отличная работа! Вы создали четыре модели регрессии за один урок и улучшили качество модели до 97%. В последнем разделе о регрессии вы узнаете о логистической регрессии для определения категорий. --- ## 🚀Задание Протестируйте несколько различных переменных в этом ноутбуке, чтобы увидеть, как корреляция влияет на точность модели. ## [Викторина после лекции](https://ff-quizzes.netlify.app/en/ml/) ## Обзор и самостоятельное изучение В этом уроке мы изучили линейную регрессию. Существуют и другие важные типы регрессии. Прочитайте о методах Stepwise, Ridge, Lasso и Elasticnet. Хороший курс для изучения — [курс статистического обучения Стэнфорда](https://online.stanford.edu/courses/sohs-ystatslearning-statistical-learning). ## Задание [Создайте модель](assignment.md) --- **Отказ от ответственности**: Этот документ был переведен с помощью сервиса автоматического перевода [Co-op Translator](https://github.com/Azure/co-op-translator). Несмотря на наши усилия по обеспечению точности, автоматические переводы могут содержать ошибки или неточности. Оригинальный документ на его родном языке следует считать авторитетным источником. Для получения критически важной информации рекомендуется профессиональный перевод человеком. Мы не несем ответственности за любые недоразумения или неправильные интерпретации, возникшие в результате использования данного перевода.