# Construirea unui model de regresie folosind Scikit-learn: patru metode de regresie
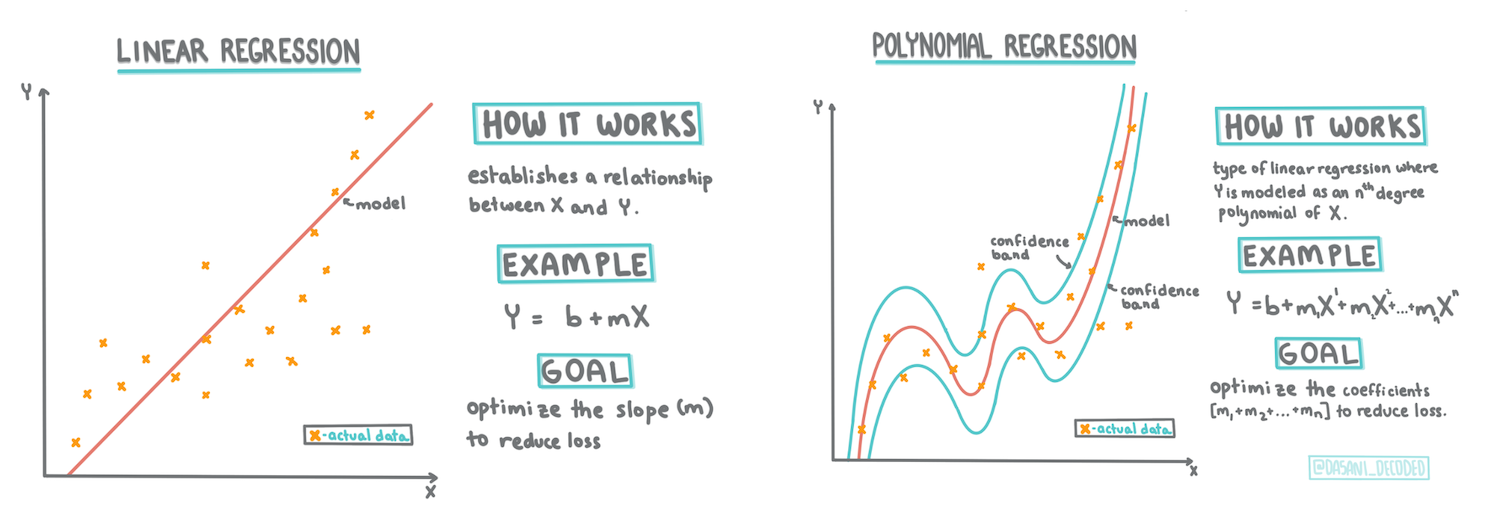
> Infografic de [Dasani Madipalli](https://twitter.com/dasani_decoded)
## [Chestionar înainte de lecție](https://ff-quizzes.netlify.app/en/ml/)
> ### [Această lecție este disponibilă și în R!](../../../../2-Regression/3-Linear/solution/R/lesson_3.html)
### Introducere
Până acum, ai explorat ce este regresia folosind date de exemplu colectate din setul de date privind prețurile dovlecilor, pe care îl vom folosi pe parcursul acestei lecții. De asemenea, ai vizualizat aceste date folosind Matplotlib.
Acum ești pregătit să aprofundezi regresia pentru ML. Deși vizualizarea te ajută să înțelegi datele, adevărata putere a Machine Learning vine din _antrenarea modelelor_. Modelele sunt antrenate pe date istorice pentru a captura automat dependențele dintre date și permit prezicerea rezultatelor pentru date noi, pe care modelul nu le-a văzut anterior.
În această lecție, vei învăța mai multe despre două tipuri de regresie: _regresia liniară de bază_ și _regresia polinomială_, împreună cu o parte din matematica care stă la baza acestor tehnici. Aceste modele ne vor permite să prezicem prețurile dovlecilor în funcție de diferite date de intrare.
[](https://youtu.be/CRxFT8oTDMg "ML pentru începători - Înțelegerea regresiei liniare")
> 🎥 Fă clic pe imaginea de mai sus pentru un scurt videoclip despre regresia liniară.
> Pe parcursul acestui curriculum, presupunem cunoștințe minime de matematică și încercăm să o facem accesibilă pentru studenții din alte domenii, așa că fii atent la notițe, 🧮 explicații, diagrame și alte instrumente de învățare care să ajute la înțelegere.
### Cerințe preliminare
Ar trebui să fii familiarizat până acum cu structura datelor despre dovleci pe care le examinăm. Le poți găsi preîncărcate și pre-curățate în fișierul _notebook.ipynb_ al acestei lecții. În fișier, prețul dovlecilor este afișat per bushel într-un nou cadru de date. Asigură-te că poți rula aceste notebook-uri în kernel-uri din Visual Studio Code.
### Pregătire
Ca o reamintire, încarci aceste date pentru a pune întrebări despre ele.
- Care este cel mai bun moment pentru a cumpăra dovleci?
- Ce preț pot să mă aștept pentru o cutie de dovleci miniaturali?
- Ar trebui să îi cumpăr în coșuri de jumătate de bushel sau în cutii de 1 1/9 bushel?
Să continuăm să explorăm aceste date.
În lecția anterioară, ai creat un cadru de date Pandas și l-ai populat cu o parte din setul de date original, standardizând prețurile pe bushel. Procedând astfel, însă, ai reușit să colectezi doar aproximativ 400 de puncte de date și doar pentru lunile de toamnă.
Aruncă o privire la datele preîncărcate în notebook-ul care însoțește această lecție. Datele sunt preîncărcate și un grafic inițial de tip scatterplot este creat pentru a arăta datele lunare. Poate putem obține mai multe detalii despre natura datelor curățându-le mai mult.
## O linie de regresie liniară
Așa cum ai învățat în Lecția 1, scopul unui exercițiu de regresie liniară este să poți trasa o linie pentru:
- **Afișarea relațiilor dintre variabile**. Afișarea relației dintre variabile
- **Realizarea de predicții**. Realizarea de predicții precise despre unde ar cădea un nou punct de date în raport cu acea linie.
Este tipic pentru **Regresia Least-Squares** să traseze acest tip de linie. Termenul 'least-squares' înseamnă că toate punctele de date din jurul liniei de regresie sunt ridicate la pătrat și apoi adunate. Ideal, suma finală este cât mai mică posibil, deoarece dorim un număr redus de erori, sau `least-squares`.
Facem acest lucru deoarece dorim să modelăm o linie care are cea mai mică distanță cumulativă față de toate punctele noastre de date. De asemenea, ridicăm termenii la pătrat înainte de a-i aduna, deoarece ne preocupă magnitudinea lor, nu direcția.
> **🧮 Arată-mi matematica**
>
> Această linie, numită _linia de cea mai bună potrivire_, poate fi exprimată prin [o ecuație](https://en.wikipedia.org/wiki/Simple_linear_regression):
>
> ```
> Y = a + bX
> ```
>
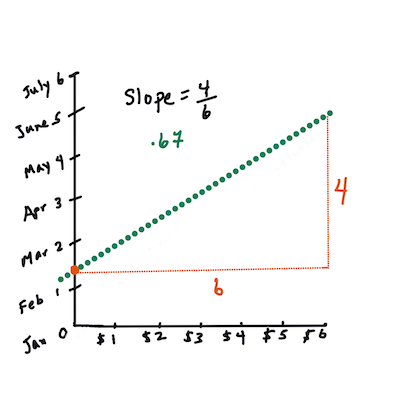
> `X` este 'variabila explicativă'. `Y` este 'variabila dependentă'. Panta liniei este `b`, iar `a` este interceptul pe axa Y, care se referă la valoarea lui `Y` când `X = 0`.
>
>
>
> Mai întâi, calculează panta `b`. Infografic de [Jen Looper](https://twitter.com/jenlooper)
>
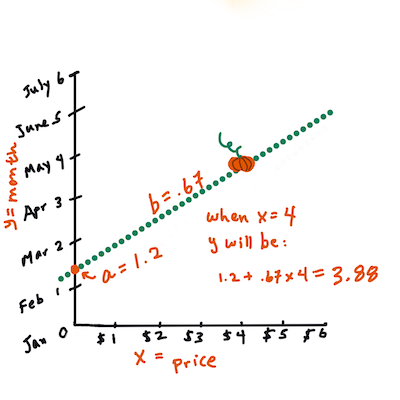
> Cu alte cuvinte, referindu-ne la întrebarea originală despre datele dovlecilor: "prezice prețul unui dovleac per bushel în funcție de lună", `X` ar fi prețul, iar `Y` ar fi luna vânzării.
>
>
>
> Calculează valoarea lui Y. Dacă plătești în jur de 4 dolari, trebuie să fie aprilie! Infografic de [Jen Looper](https://twitter.com/jenlooper)
>
> Matematica care calculează linia trebuie să demonstreze panta liniei, care depinde și de interceptul, sau unde se află `Y` când `X = 0`.
>
> Poți observa metoda de calcul pentru aceste valori pe site-ul [Math is Fun](https://www.mathsisfun.com/data/least-squares-regression.html). Vizitează și [acest calculator Least-squares](https://www.mathsisfun.com/data/least-squares-calculator.html) pentru a vedea cum valorile numerelor influențează linia.
## Corelație
Un alt termen de înțeles este **Coeficientul de Corelație** între variabilele X și Y date. Folosind un scatterplot, poți vizualiza rapid acest coeficient. Un grafic cu puncte de date distribuite într-o linie ordonată are o corelație mare, dar un grafic cu puncte de date distribuite aleatoriu între X și Y are o corelație mică.
Un model de regresie liniară bun va fi unul care are un Coeficient de Corelație mare (mai aproape de 1 decât de 0) folosind metoda Least-Squares Regression cu o linie de regresie.
✅ Rulează notebook-ul care însoțește această lecție și uită-te la scatterplot-ul Lună-Preț. Datele care asociază Luna cu Prețul pentru vânzările de dovleci par să aibă o corelație mare sau mică, conform interpretării tale vizuale a scatterplot-ului? Se schimbă acest lucru dacă folosești o măsură mai detaliată în loc de `Lună`, de exemplu *ziua anului* (adică numărul de zile de la începutul anului)?
În codul de mai jos, vom presupune că am curățat datele și am obținut un cadru de date numit `new_pumpkins`, similar cu următorul:
ID | Lună | ZiuaAnului | Tip | Oraș | Pachet | Preț Minim | Preț Maxim | Preț
---|------|------------|-----|------|--------|------------|------------|------
70 | 9 | 267 | TIP PLĂCINTĂ | BALTIMORE | 1 1/9 bushel cartons | 15.0 | 15.0 | 13.636364
71 | 9 | 267 | TIP PLĂCINTĂ | BALTIMORE | 1 1/9 bushel cartons | 18.0 | 18.0 | 16.363636
72 | 10 | 274 | TIP PLĂCINTĂ | BALTIMORE | 1 1/9 bushel cartons | 18.0 | 18.0 | 16.363636
73 | 10 | 274 | TIP PLĂCINTĂ | BALTIMORE | 1 1/9 bushel cartons | 17.0 | 17.0 | 15.454545
74 | 10 | 281 | TIP PLĂCINTĂ | BALTIMORE | 1 1/9 bushel cartons | 15.0 | 15.0 | 13.636364
> Codul pentru curățarea datelor este disponibil în [`notebook.ipynb`](../../../../2-Regression/3-Linear/notebook.ipynb). Am efectuat aceleași pași de curățare ca în lecția anterioară și am calculat coloana `ZiuaAnului` folosind următoarea expresie:
```python
day_of_year = pd.to_datetime(pumpkins['Date']).apply(lambda dt: (dt-datetime(dt.year,1,1)).days)
```
Acum că ai o înțelegere a matematicii din spatele regresiei liniare, să creăm un model de regresie pentru a vedea dacă putem prezice care pachet de dovleci va avea cele mai bune prețuri. Cineva care cumpără dovleci pentru o grădină tematică de sărbători ar putea dori aceste informații pentru a optimiza achizițiile de pachete de dovleci pentru grădină.
## Căutarea corelației
[](https://youtu.be/uoRq-lW2eQo "ML pentru începători - Căutarea corelației: cheia regresiei liniare")
> 🎥 Fă clic pe imaginea de mai sus pentru un scurt videoclip despre corelație.
Din lecția anterioară, probabil ai observat că prețul mediu pentru diferite luni arată astfel:
Acest lucru sugerează că ar trebui să existe o anumită corelație, iar noi putem încerca să antrenăm un model de regresie liniară pentru a prezice relația dintre `Lună` și `Preț`, sau dintre `ZiuaAnului` și `Preț`. Iată scatterplot-ul care arată ultima relație:
Să vedem dacă există o corelație folosind funcția `corr`:
```python
print(new_pumpkins['Month'].corr(new_pumpkins['Price']))
print(new_pumpkins['DayOfYear'].corr(new_pumpkins['Price']))
```
Se pare că corelația este destul de mică, -0.15 pentru `Lună` și -0.17 pentru `ZiuaAnului`, dar ar putea exista o altă relație importantă. Se pare că există diferite grupuri de prețuri corespunzătoare diferitelor varietăți de dovleci. Pentru a confirma această ipoteză, să reprezentăm fiecare categorie de dovleci folosind o culoare diferită. Prin transmiterea unui parametru `ax` funcției de plotare `scatter`, putem reprezenta toate punctele pe același grafic:
```python
ax=None
colors = ['red','blue','green','yellow']
for i,var in enumerate(new_pumpkins['Variety'].unique()):
df = new_pumpkins[new_pumpkins['Variety']==var]
ax = df.plot.scatter('DayOfYear','Price',ax=ax,c=colors[i],label=var)
```
Investigația noastră sugerează că varietatea are un efect mai mare asupra prețului general decât data efectivă de vânzare. Putem vedea acest lucru cu un grafic de tip bară:
```python
new_pumpkins.groupby('Variety')['Price'].mean().plot(kind='bar')
```
Să ne concentrăm pentru moment doar pe o singură varietate de dovleci, 'tip plăcintă', și să vedem ce efect are data asupra prețului:
```python
pie_pumpkins = new_pumpkins[new_pumpkins['Variety']=='PIE TYPE']
pie_pumpkins.plot.scatter('DayOfYear','Price')
```
Dacă acum calculăm corelația dintre `Preț` și `ZiuaAnului` folosind funcția `corr`, vom obține ceva în jur de `-0.27` - ceea ce înseamnă că antrenarea unui model predictiv are sens.
> Înainte de a antrena un model de regresie liniară, este important să ne asigurăm că datele noastre sunt curate. Regresia liniară nu funcționează bine cu valori lipsă, astfel încât este logic să eliminăm toate celulele goale:
```python
pie_pumpkins.dropna(inplace=True)
pie_pumpkins.info()
```
O altă abordare ar fi să completăm valorile lipsă cu valorile medii din coloana corespunzătoare.
## Regresie liniară simplă
[](https://youtu.be/e4c_UP2fSjg "ML pentru începători - Regresie liniară și polinomială folosind Scikit-learn")
> 🎥 Fă clic pe imaginea de mai sus pentru un scurt videoclip despre regresia liniară și polinomială.
Pentru a antrena modelul nostru de regresie liniară, vom folosi biblioteca **Scikit-learn**.
```python
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
```
Începem prin separarea valorilor de intrare (caracteristici) și a ieșirii așteptate (eticheta) în array-uri numpy separate:
```python
X = pie_pumpkins['DayOfYear'].to_numpy().reshape(-1,1)
y = pie_pumpkins['Price']
```
> Observă că a trebuit să aplicăm `reshape` pe datele de intrare pentru ca pachetul de regresie liniară să le înțeleagă corect. Regresia liniară așteaptă un array 2D ca intrare, unde fiecare rând al array-ului corespunde unui vector de caracteristici de intrare. În cazul nostru, deoarece avem doar o singură intrare - avem nevoie de un array cu forma N×1, unde N este dimensiunea setului de date.
Apoi, trebuie să împărțim datele în seturi de antrenament și test, astfel încât să putem valida modelul nostru după antrenament:
```python
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
```
În cele din urmă, antrenarea modelului de regresie liniară propriu-zis durează doar două linii de cod. Definim obiectul `LinearRegression` și îl ajustăm la datele noastre folosind metoda `fit`:
```python
lin_reg = LinearRegression()
lin_reg.fit(X_train,y_train)
```
Obiectul `LinearRegression` după ajustare conține toate coeficienții regresiei, care pot fi accesați folosind proprietatea `.coef_`. În cazul nostru, există doar un coeficient, care ar trebui să fie în jur de `-0.017`. Acest lucru înseamnă că prețurile par să scadă puțin în timp, dar nu prea mult, aproximativ 2 cenți pe zi. De asemenea, putem accesa punctul de intersecție al regresiei cu axa Y folosind `lin_reg.intercept_` - va fi în jur de `21` în cazul nostru, indicând prețul de la începutul anului.
Pentru a vedea cât de precis este modelul nostru, putem prezice prețurile pe un set de date de test și apoi măsura cât de apropiate sunt predicțiile noastre de valorile așteptate. Acest lucru poate fi realizat folosind metrica mean square error (MSE), care este media tuturor diferențelor pătrate dintre valoarea așteptată și cea prezisă.
```python
pred = lin_reg.predict(X_test)
mse = np.sqrt(mean_squared_error(y_test,pred))
print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)')
```
Eroarea noastră pare să fie în jur de 2 puncte, ceea ce reprezintă ~17%. Nu prea bine. Un alt indicator al calității modelului este **coeficientul de determinare**, care poate fi obținut astfel:
```python
score = lin_reg.score(X_train,y_train)
print('Model determination: ', score)
```
Dacă valoarea este 0, înseamnă că modelul nu ia în considerare datele de intrare și acționează ca *cel mai slab predictor liniar*, care este pur și simplu valoarea medie a rezultatului. Valoarea de 1 înseamnă că putem prezice perfect toate rezultatele așteptate. În cazul nostru, coeficientul este în jur de 0.06, ceea ce este destul de scăzut.
Putem, de asemenea, să reprezentăm grafic datele de testare împreună cu linia de regresie pentru a vedea mai bine cum funcționează regresia în cazul nostru:
```python
plt.scatter(X_test,y_test)
plt.plot(X_test,pred)
```
## Regresie Polinomială
Un alt tip de regresie liniară este regresia polinomială. Deși uneori există o relație liniară între variabile - cu cât dovleacul este mai mare în volum, cu atât prețul este mai mare - uneori aceste relații nu pot fi reprezentate ca un plan sau o linie dreaptă.
✅ Iată [câteva exemple](https://online.stat.psu.edu/stat501/lesson/9/9.8) de date care ar putea utiliza regresia polinomială.
Privește din nou relația dintre Dată și Preț. Acest scatterplot pare să fie analizat neapărat printr-o linie dreaptă? Nu pot prețurile să fluctueze? În acest caz, poți încerca regresia polinomială.
✅ Polinoamele sunt expresii matematice care pot consta din una sau mai multe variabile și coeficienți.
Regresia polinomială creează o linie curbată pentru a se potrivi mai bine datelor neliniare. În cazul nostru, dacă includem o variabilă pătratică `DayOfYear` în datele de intrare, ar trebui să putem ajusta datele noastre cu o curbă parabolică, care va avea un minim într-un anumit punct al anului.
Scikit-learn include o [API pipeline](https://scikit-learn.org/stable/modules/generated/sklearn.pipeline.make_pipeline.html?highlight=pipeline#sklearn.pipeline.make_pipeline) utilă pentru a combina diferite etape de procesare a datelor. Un **pipeline** este un lanț de **estimatori**. În cazul nostru, vom crea un pipeline care mai întâi adaugă caracteristici polinomiale modelului nostru, apoi antrenează regresia:
```python
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression())
pipeline.fit(X_train,y_train)
```
Utilizarea `PolynomialFeatures(2)` înseamnă că vom include toate polinoamele de gradul doi din datele de intrare. În cazul nostru, aceasta va însemna doar `DayOfYear`2, dar având două variabile de intrare X și Y, aceasta va adăuga X2, XY și Y2. Putem folosi și polinoame de grad mai mare dacă dorim.
Pipeline-urile pot fi utilizate în același mod ca obiectul original `LinearRegression`, adică putem aplica `fit` pipeline-ului și apoi utiliza `predict` pentru a obține rezultatele predicției. Iată graficul care arată datele de testare și curba de aproximare:
Folosind regresia polinomială, putem obține un MSE ușor mai mic și un coeficient de determinare mai mare, dar nu semnificativ. Trebuie să luăm în considerare alte caracteristici!
> Poți observa că prețurile minime ale dovlecilor sunt observate undeva în jurul Halloween-ului. Cum poți explica acest lucru?
🎃 Felicitări, tocmai ai creat un model care poate ajuta la prezicerea prețului dovlecilor pentru plăcintă. Probabil poți repeta aceeași procedură pentru toate tipurile de dovleci, dar ar fi obositor. Să învățăm acum cum să luăm în considerare varietatea dovlecilor în modelul nostru!
## Caracteristici Categoriale
În lumea ideală, ne dorim să putem prezice prețurile pentru diferite varietăți de dovleci folosind același model. Totuși, coloana `Variety` este oarecum diferită de coloane precum `Month`, deoarece conține valori non-numerice. Astfel de coloane sunt numite **categoriale**.
[](https://youtu.be/DYGliioIAE0 "ML pentru începători - Predicții cu caracteristici categoriale folosind regresia liniară")
> 🎥 Fă clic pe imaginea de mai sus pentru un scurt videoclip despre utilizarea caracteristicilor categoriale.
Aici poți vedea cum prețul mediu depinde de varietate:
Pentru a lua în considerare varietatea, mai întâi trebuie să o convertim într-o formă numerică, sau să o **codificăm**. Există mai multe moduri în care putem face acest lucru:
* Codificarea numerică simplă va construi un tabel cu diferite varietăți și apoi va înlocui numele varietății cu un index din acel tabel. Aceasta nu este cea mai bună idee pentru regresia liniară, deoarece regresia liniară ia valoarea numerică reală a indexului și o adaugă la rezultat, înmulțind-o cu un coeficient. În cazul nostru, relația dintre numărul indexului și preț este clar neliniară, chiar dacă ne asigurăm că indicii sunt ordonați într-un mod specific.
* **Codificarea one-hot** va înlocui coloana `Variety` cu 4 coloane diferite, câte una pentru fiecare varietate. Fiecare coloană va conține `1` dacă rândul corespunzător este de o anumită varietate și `0` în caz contrar. Aceasta înseamnă că vor exista patru coeficienți în regresia liniară, câte unul pentru fiecare varietate de dovleac, responsabili pentru "prețul de pornire" (sau mai degrabă "prețul suplimentar") pentru acea varietate specifică.
Codul de mai jos arată cum putem codifica one-hot o varietate:
```python
pd.get_dummies(new_pumpkins['Variety'])
```
ID | FAIRYTALE | MINIATURE | MIXED HEIRLOOM VARIETIES | PIE TYPE
----|-----------|-----------|--------------------------|----------
70 | 0 | 0 | 0 | 1
71 | 0 | 0 | 0 | 1
... | ... | ... | ... | ...
1738 | 0 | 1 | 0 | 0
1739 | 0 | 1 | 0 | 0
1740 | 0 | 1 | 0 | 0
1741 | 0 | 1 | 0 | 0
1742 | 0 | 1 | 0 | 0
Pentru a antrena regresia liniară folosind varietatea codificată one-hot ca intrare, trebuie doar să inițializăm corect datele `X` și `y`:
```python
X = pd.get_dummies(new_pumpkins['Variety'])
y = new_pumpkins['Price']
```
Restul codului este același cu cel pe care l-am folosit mai sus pentru a antrena regresia liniară. Dacă încerci, vei vedea că eroarea medie pătratică este aproximativ aceeași, dar obținem un coeficient de determinare mult mai mare (~77%). Pentru a obține predicții și mai precise, putem lua în considerare mai multe caracteristici categoriale, precum și caracteristici numerice, cum ar fi `Month` sau `DayOfYear`. Pentru a obține un array mare de caracteristici, putem folosi `join`:
```python
X = pd.get_dummies(new_pumpkins['Variety']) \
.join(new_pumpkins['Month']) \
.join(pd.get_dummies(new_pumpkins['City'])) \
.join(pd.get_dummies(new_pumpkins['Package']))
y = new_pumpkins['Price']
```
Aici luăm în considerare și `City` și tipul de `Package`, ceea ce ne oferă un MSE de 2.84 (10%) și un coeficient de determinare de 0.94!
## Punând totul împreună
Pentru a crea cel mai bun model, putem folosi date combinate (categoriale codificate one-hot + numerice) din exemplul de mai sus împreună cu regresia polinomială. Iată codul complet pentru confortul tău:
```python
# set up training data
X = pd.get_dummies(new_pumpkins['Variety']) \
.join(new_pumpkins['Month']) \
.join(pd.get_dummies(new_pumpkins['City'])) \
.join(pd.get_dummies(new_pumpkins['Package']))
y = new_pumpkins['Price']
# make train-test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# setup and train the pipeline
pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression())
pipeline.fit(X_train,y_train)
# predict results for test data
pred = pipeline.predict(X_test)
# calculate MSE and determination
mse = np.sqrt(mean_squared_error(y_test,pred))
print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)')
score = pipeline.score(X_train,y_train)
print('Model determination: ', score)
```
Acest lucru ar trebui să ne ofere cel mai bun coeficient de determinare de aproape 97% și MSE=2.23 (~8% eroare de predicție).
| Model | MSE | Determinare |
|-------|-----|-------------|
| `DayOfYear` Liniar | 2.77 (17.2%) | 0.07 |
| `DayOfYear` Polinomial | 2.73 (17.0%) | 0.08 |
| `Variety` Liniar | 5.24 (19.7%) | 0.77 |
| Toate caracteristicile Liniar | 2.84 (10.5%) | 0.94 |
| Toate caracteristicile Polinomial | 2.23 (8.25%) | 0.97 |
🏆 Bravo! Ai creat patru modele de regresie într-o singură lecție și ai îmbunătățit calitatea modelului la 97%. În secțiunea finală despre regresie, vei învăța despre regresia logistică pentru a determina categorii.
---
## 🚀Provocare
Testează mai multe variabile diferite în acest notebook pentru a vedea cum corelația corespunde cu acuratețea modelului.
## [Quiz post-lectură](https://ff-quizzes.netlify.app/en/ml/)
## Recapitulare & Studiu Individual
În această lecție am învățat despre regresia liniară. Există alte tipuri importante de regresie. Citește despre tehnicile Stepwise, Ridge, Lasso și Elasticnet. Un curs bun pentru a învăța mai multe este [cursul de învățare statistică de la Stanford](https://online.stanford.edu/courses/sohs-ystatslearning-statistical-learning).
## Temă
[Construiește un model](assignment.md)
---
**Declinare de responsabilitate**:
Acest document a fost tradus folosind serviciul de traducere AI [Co-op Translator](https://github.com/Azure/co-op-translator). Deși ne străduim să asigurăm acuratețea, vă rugăm să fiți conștienți că traducerile automate pot conține erori sau inexactități. Documentul original în limba sa natală ar trebui considerat sursa autoritară. Pentru informații critice, se recomandă traducerea profesională realizată de un specialist uman. Nu ne asumăm responsabilitatea pentru eventualele neînțelegeri sau interpretări greșite care pot apărea din utilizarea acestei traduceri.