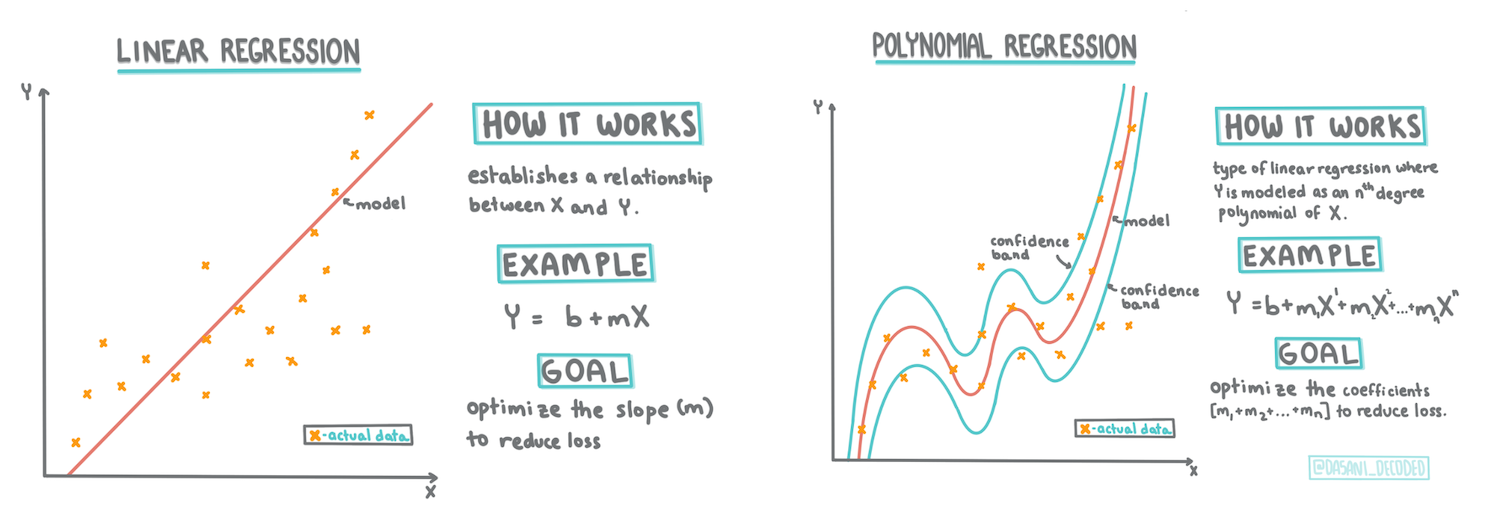
# Bygg en regresjonsmodell med Scikit-learn: regresjon på fire måter  > Infografikk av [Dasani Madipalli](https://twitter.com/dasani_decoded) ## [Quiz før forelesning](https://ff-quizzes.netlify.app/en/ml/) > ### [Denne leksjonen er også tilgjengelig i R!](../../../../2-Regression/3-Linear/solution/R/lesson_3.html) ### Introduksjon Så langt har du utforsket hva regresjon er med eksempeldata hentet fra gresskarpris-datasettet som vi skal bruke gjennom hele denne leksjonen. Du har også visualisert det ved hjelp av Matplotlib. Nå er du klar til å dykke dypere inn i regresjon for maskinlæring. Mens visualisering hjelper deg med å forstå data, ligger den virkelige kraften i maskinlæring i _å trene modeller_. Modeller trenes på historiske data for automatisk å fange opp datamønstre, og de lar deg forutsi utfall for nye data som modellen ikke har sett før. I denne leksjonen vil du lære mer om to typer regresjon: _grunnleggende lineær regresjon_ og _polynomisk regresjon_, sammen med noe av matematikken som ligger til grunn for disse teknikkene. Disse modellene vil hjelpe oss med å forutsi gresskarpriser basert på ulike inngangsdata. [](https://youtu.be/CRxFT8oTDMg "ML for nybegynnere - Forstå lineær regresjon") > 🎥 Klikk på bildet over for en kort videooversikt over lineær regresjon. > Gjennom hele dette kurset antar vi minimal kunnskap om matematikk og søker å gjøre det tilgjengelig for studenter fra andre felt. Se etter notater, 🧮 utrop, diagrammer og andre læringsverktøy for å hjelpe med forståelsen. ### Forutsetninger Du bør nå være kjent med strukturen til gresskar-datasettet vi undersøker. Du finner det forhåndslastet og forhåndsrenset i denne leksjonens _notebook.ipynb_-fil. I filen vises gresskarprisen per bushel i en ny data frame. Sørg for at du kan kjøre disse notatbøkene i kjerner i Visual Studio Code. ### Forberedelse Som en påminnelse, du laster inn disse dataene for å stille spørsmål til dem. - Når er det best å kjøpe gresskar? - Hvilken pris kan jeg forvente for en kasse med miniatyrgresskar? - Bør jeg kjøpe dem i halv-bushelkurver eller i 1 1/9 bushel-esker? La oss fortsette å grave i disse dataene. I forrige leksjon opprettet du en Pandas data frame og fylte den med en del av det opprinnelige datasettet, og standardiserte prisen per bushel. Ved å gjøre det var du imidlertid bare i stand til å samle rundt 400 datapunkter, og kun for høstmånedene. Ta en titt på dataene som vi har forhåndslastet i denne leksjonens tilhørende notatbok. Dataene er forhåndslastet, og et første spredningsdiagram er laget for å vise månedsdata. Kanskje vi kan få litt mer innsikt i dataene ved å rense dem ytterligere. ## En lineær regresjonslinje Som du lærte i leksjon 1, er målet med en lineær regresjonsøvelse å kunne tegne en linje for å: - **Vise variabelsammenhenger**. Vise forholdet mellom variabler - **Gjøre forutsigelser**. Gjøre nøyaktige forutsigelser om hvor et nytt datapunkt vil falle i forhold til den linjen. Det er typisk for **minste kvadraters regresjon** å tegne denne typen linje. Begrepet 'minste kvadrater' betyr at alle datapunktene rundt regresjonslinjen kvadreres og deretter summeres. Ideelt sett er denne summen så liten som mulig, fordi vi ønsker et lavt antall feil, eller `minste kvadrater`. Vi gjør dette fordi vi ønsker å modellere en linje som har minst mulig kumulativ avstand fra alle datapunktene våre. Vi kvadrerer også termene før vi legger dem sammen, siden vi er opptatt av størrelsen snarere enn retningen. 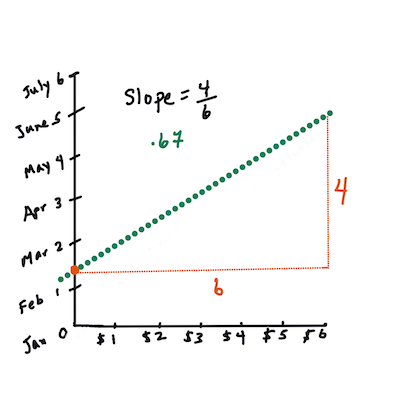> **🧮 Vis meg matematikken** > > Denne linjen, kalt _linjen for beste tilpasning_, kan uttrykkes ved [en ligning](https://en.wikipedia.org/wiki/Simple_linear_regression): > > ``` > Y = a + bX > ``` > > `X` er den 'forklarende variabelen'. `Y` er den 'avhengige variabelen'. Stigningen på linjen er `b`, og `a` er skjæringspunktet med y-aksen, som refererer til verdien av `Y` når `X = 0`. > > > > Først, beregn stigningen `b`. 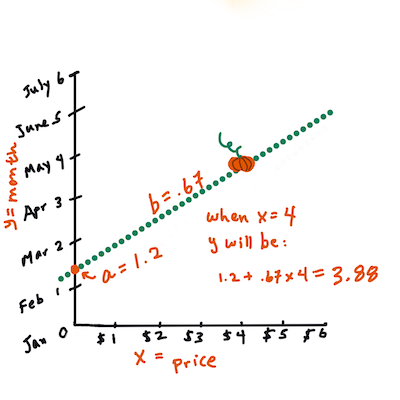Infografikk av [Jen Looper](https://twitter.com/jenlooper) > > Med andre ord, og med henvisning til det opprinnelige spørsmålet om gresskar-dataene: "forutsi prisen på et gresskar per bushel etter måned", ville `X` referere til prisen og `Y` til salgsdatoen. > > > > Beregn verdien av Y. Hvis du betaler rundt $4, må det være april! Infografikk av [Jen Looper](https://twitter.com/jenlooper) > > Matematikk som beregner linjen må vise stigningen på linjen, som også avhenger av skjæringspunktet, eller hvor `Y` er plassert når `X = 0`. > > Du kan se metoden for beregning av disse verdiene på nettstedet [Math is Fun](https://www.mathsisfun.com/data/least-squares-regression.html). Besøk også [denne minste kvadraters kalkulatoren](https://www.mathsisfun.com/data/least-squares-calculator.html) for å se hvordan tallverdiene påvirker linjen. ## Korrelasjon Et annet begrep å forstå er **korrelasjonskoeffisienten** mellom gitte X- og Y-variabler. Ved hjelp av et spredningsdiagram kan du raskt visualisere denne koeffisienten. Et diagram med datapunkter spredt i en ryddig linje har høy korrelasjon, men et diagram med datapunkter spredt overalt mellom X og Y har lav korrelasjon. En god lineær regresjonsmodell vil være en som har en høy (nærmere 1 enn 0) korrelasjonskoeffisient ved bruk av minste kvadraters regresjonsmetode med en regresjonslinje. ✅ Kjør notatboken som følger med denne leksjonen, og se på spredningsdiagrammet for måned til pris. Ser dataene som knytter måned til pris for gresskarsalg ut til å ha høy eller lav korrelasjon, ifølge din visuelle tolkning av spredningsdiagrammet? Endrer det seg hvis du bruker en mer detaljert måling i stedet for `Måned`, for eksempel *dag i året* (dvs. antall dager siden begynnelsen av året)? I koden nedenfor antar vi at vi har renset dataene og fått en data frame kalt `new_pumpkins`, som ligner på følgende: ID | Måned | DagIÅret | Sort | By | Pakke | Lav pris | Høy pris | Pris ---|-------|----------|------|-----|--------|----------|----------|----- 70 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 15.0 | 15.0 | 13.636364 71 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 18.0 | 18.0 | 16.363636 72 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 18.0 | 18.0 | 16.363636 73 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 17.0 | 17.0 | 15.454545 74 | 10 | 281 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 15.0 | 15.0 | 13.636364 > Koden for å rense dataene er tilgjengelig i [`notebook.ipynb`](../../../../2-Regression/3-Linear/notebook.ipynb). Vi har utført de samme rensetrinnene som i forrige leksjon, og har beregnet `DagIÅret`-kolonnen ved hjelp av følgende uttrykk: ```python day_of_year = pd.to_datetime(pumpkins['Date']).apply(lambda dt: (dt-datetime(dt.year,1,1)).days) ``` Nå som du har en forståelse av matematikken bak lineær regresjon, la oss lage en regresjonsmodell for å se om vi kan forutsi hvilken pakke med gresskar som vil ha de beste prisene. Noen som kjøper gresskar til en høstfest kan ha nytte av denne informasjonen for å optimalisere kjøpene sine. ## Lete etter korrelasjon [](https://youtu.be/uoRq-lW2eQo "ML for nybegynnere - Lete etter korrelasjon: Nøkkelen til lineær regresjon") > 🎥 Klikk på bildet over for en kort videooversikt over korrelasjon. Fra forrige leksjon har du sannsynligvis sett at gjennomsnittsprisen for ulike måneder ser slik ut: Dette antyder at det bør være en viss korrelasjon, og vi kan prøve å trene en lineær regresjonsmodell for å forutsi forholdet mellom `Måned` og `Pris`, eller mellom `DagIÅret` og `Pris`. Her er spredningsdiagrammet som viser det sistnevnte forholdet: La oss se om det er en korrelasjon ved hjelp av `corr`-funksjonen: ```python print(new_pumpkins['Month'].corr(new_pumpkins['Price'])) print(new_pumpkins['DayOfYear'].corr(new_pumpkins['Price'])) ``` Det ser ut til at korrelasjonen er ganske liten, -0.15 for `Måned` og -0.17 for `DagIÅret`, men det kan være et annet viktig forhold. Det ser ut til at det er forskjellige prisgrupper som tilsvarer ulike gresskarsorter. For å bekrefte denne hypotesen, la oss plotte hver gresskarkategori med en annen farge. Ved å sende en `ax`-parameter til `scatter`-plottefunksjonen kan vi plotte alle punkter på samme graf: ```python ax=None colors = ['red','blue','green','yellow'] for i,var in enumerate(new_pumpkins['Variety'].unique()): df = new_pumpkins[new_pumpkins['Variety']==var] ax = df.plot.scatter('DayOfYear','Price',ax=ax,c=colors[i],label=var) ``` Vår undersøkelse antyder at sorten har større effekt på den totale prisen enn selve salgsdatoen. Vi kan se dette med et stolpediagram: ```python new_pumpkins.groupby('Variety')['Price'].mean().plot(kind='bar') ``` La oss for øyeblikket fokusere kun på én gresskarsort, 'pie type', og se hvilken effekt datoen har på prisen: ```python pie_pumpkins = new_pumpkins[new_pumpkins['Variety']=='PIE TYPE'] pie_pumpkins.plot.scatter('DayOfYear','Price') ``` Hvis vi nå beregner korrelasjonen mellom `Pris` og `DagIÅret` ved hjelp av `corr`-funksjonen, vil vi få noe som `-0.27` - noe som betyr at det gir mening å trene en prediktiv modell. > Før du trener en lineær regresjonsmodell, er det viktig å sørge for at dataene våre er rene. Lineær regresjon fungerer ikke godt med manglende verdier, så det gir mening å fjerne alle tomme celler: ```python pie_pumpkins.dropna(inplace=True) pie_pumpkins.info() ``` En annen tilnærming ville være å fylle de tomme verdiene med gjennomsnittsverdier fra den tilsvarende kolonnen. ## Enkel lineær regresjon [](https://youtu.be/e4c_UP2fSjg "ML for nybegynnere - Lineær og polynomisk regresjon med Scikit-learn") > 🎥 Klikk på bildet over for en kort videooversikt over lineær og polynomisk regresjon. For å trene vår lineære regresjonsmodell, vil vi bruke **Scikit-learn**-biblioteket. ```python from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error from sklearn.model_selection import train_test_split ``` Vi starter med å skille inngangsverdier (funksjoner) og forventet utgang (etikett) i separate numpy-arrays: ```python X = pie_pumpkins['DayOfYear'].to_numpy().reshape(-1,1) y = pie_pumpkins['Price'] ``` > Merk at vi måtte utføre `reshape` på inngangsdataene for at pakken for lineær regresjon skulle forstå dem riktig. Lineær regresjon forventer et 2D-array som inngang, hvor hver rad i arrayet tilsvarer en vektor av inngangsfunksjoner. I vårt tilfelle, siden vi bare har én inngang, trenger vi et array med formen N×1, hvor N er datasettets størrelse. Deretter må vi dele dataene inn i trenings- og testdatasett, slik at vi kan validere modellen vår etter trening: ```python X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) ``` Til slutt tar det bare to linjer med kode å trene den faktiske lineære regresjonsmodellen. Vi definerer `LinearRegression`-objektet og tilpasser det til dataene våre ved hjelp av `fit`-metoden: ```python lin_reg = LinearRegression() lin_reg.fit(X_train,y_train) ``` `LinearRegression`-objektet inneholder etter `fit`-prosessen alle koeffisientene for regresjonen, som kan nås ved hjelp av `.coef_`-egenskapen. I vårt tilfelle er det bare én koeffisient, som bør være rundt `-0.017`. Dette betyr at prisene ser ut til å synke litt over tid, men ikke mye, rundt 2 cent per dag. Vi kan også få tilgang til skjæringspunktet med Y-aksen ved hjelp av `lin_reg.intercept_` - det vil være rundt `21` i vårt tilfelle, noe som indikerer prisen ved begynnelsen av året. For å se hvor nøyaktig modellen vår er, kan vi forutsi priser på et testdatasett og deretter måle hvor nærme forutsigelsene våre er de forventede verdiene. Dette kan gjøres ved hjelp av middelkvadratfeil (MSE)-metrikken, som er gjennomsnittet av alle kvadrerte forskjeller mellom forventet og forutsagt verdi. ```python pred = lin_reg.predict(X_test) mse = np.sqrt(mean_squared_error(y_test,pred)) print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)') ``` Feilen vår ser ut til å være rundt 2 punkter, som er ~17 %. Ikke så bra. En annen indikator på modellkvalitet er **determinasjonskoeffisienten**, som kan beregnes slik: ```python score = lin_reg.score(X_train,y_train) print('Model determination: ', score) ``` Hvis verdien er 0, betyr det at modellen ikke tar hensyn til inputdata, og fungerer som den *dårligste lineære prediktoren*, som bare er gjennomsnittsverdien av resultatet. Verdien 1 betyr at vi kan perfekt forutsi alle forventede utfall. I vårt tilfelle er koeffisienten rundt 0,06, som er ganske lav. Vi kan også plotte testdata sammen med regresjonslinjen for bedre å se hvordan regresjonen fungerer i vårt tilfelle: ```python plt.scatter(X_test,y_test) plt.plot(X_test,pred) ``` ## Polynomisk regresjon En annen type lineær regresjon er polynomisk regresjon. Selv om det noen ganger er en lineær sammenheng mellom variabler - jo større gresskaret er i volum, jo høyere pris - kan det noen ganger være slik at disse sammenhengene ikke kan plottes som et plan eller en rett linje. ✅ Her er [noen flere eksempler](https://online.stat.psu.edu/stat501/lesson/9/9.8) på data som kan bruke polynomisk regresjon. Se en gang til på sammenhengen mellom dato og pris. Ser dette spredningsdiagrammet ut som det nødvendigvis bør analyseres med en rett linje? Kan ikke priser svinge? I dette tilfellet kan du prøve polynomisk regresjon. ✅ Polynomier er matematiske uttrykk som kan bestå av én eller flere variabler og koeffisienter. Polynomisk regresjon skaper en kurvet linje for bedre å tilpasse seg ikke-lineære data. I vårt tilfelle, hvis vi inkluderer en kvadrert `DayOfYear`-variabel i inputdataene, bør vi kunne tilpasse dataene våre med en parabolsk kurve, som vil ha et minimum på et bestemt punkt i løpet av året. Scikit-learn inkluderer en nyttig [pipeline-API](https://scikit-learn.org/stable/modules/generated/sklearn.pipeline.make_pipeline.html?highlight=pipeline#sklearn.pipeline.make_pipeline) for å kombinere ulike trinn i databehandlingen. En **pipeline** er en kjede av **estimators**. I vårt tilfelle vil vi lage en pipeline som først legger til polynomiske funksjoner til modellen vår, og deretter trener regresjonen: ```python from sklearn.preprocessing import PolynomialFeatures from sklearn.pipeline import make_pipeline pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression()) pipeline.fit(X_train,y_train) ``` Ved å bruke `PolynomialFeatures(2)` betyr det at vi vil inkludere alle andregrads polynomier fra inputdataene. I vårt tilfelle vil det bare bety `DayOfYear`², men gitt to inputvariabler X og Y, vil dette legge til X², XY og Y². Vi kan også bruke polynomier av høyere grad hvis vi ønsker. Pipelines kan brukes på samme måte som det opprinnelige `LinearRegression`-objektet, dvs. vi kan `fit` pipelinen, og deretter bruke `predict` for å få prediksjonsresultatene. Her er grafen som viser testdataene og tilnærmingskurven: Ved å bruke polynomisk regresjon kan vi få litt lavere MSE og høyere determinasjon, men ikke betydelig. Vi må ta hensyn til andre funksjoner! > Du kan se at de laveste gresskarprisene observeres et sted rundt Halloween. Hvordan kan du forklare dette? 🎃 Gratulerer, du har nettopp laget en modell som kan hjelpe med å forutsi prisen på pai-gresskar. Du kan sannsynligvis gjenta samme prosedyre for alle gresskartyper, men det ville være tidkrevende. La oss nå lære hvordan vi kan ta gresskarsort i betraktning i modellen vår! ## Kategoriske funksjoner I en ideell verden ønsker vi å kunne forutsi priser for ulike gresskarsorter ved hjelp av samme modell. Imidlertid er `Variety`-kolonnen litt annerledes enn kolonner som `Month`, fordi den inneholder ikke-numeriske verdier. Slike kolonner kalles **kategoriske**. [](https://youtu.be/DYGliioIAE0 "ML for nybegynnere - Kategoriske funksjoner med lineær regresjon") > 🎥 Klikk på bildet over for en kort videooversikt om bruk av kategoriske funksjoner. Her kan du se hvordan gjennomsnittsprisen avhenger av sort: For å ta sort i betraktning, må vi først konvertere den til numerisk form, eller **enkode** den. Det finnes flere måter vi kan gjøre dette på: * Enkel **numerisk enkoding** vil bygge en tabell over ulike sorter, og deretter erstatte sortnavnet med en indeks i den tabellen. Dette er ikke den beste ideen for lineær regresjon, fordi lineær regresjon tar den faktiske numeriske verdien av indeksen og legger den til resultatet, multiplisert med en koeffisient. I vårt tilfelle er sammenhengen mellom indeksnummeret og prisen tydelig ikke-lineær, selv om vi sørger for at indeksene er ordnet på en spesifikk måte. * **One-hot enkoding** vil erstatte `Variety`-kolonnen med 4 forskjellige kolonner, én for hver sort. Hver kolonne vil inneholde `1` hvis den tilsvarende raden er av en gitt sort, og `0` ellers. Dette betyr at det vil være fire koeffisienter i lineær regresjon, én for hver gresskarsort, som er ansvarlig for "startpris" (eller rettere sagt "tilleggspris") for den spesifikke sorten. Koden nedenfor viser hvordan vi kan one-hot enkode en sort: ```python pd.get_dummies(new_pumpkins['Variety']) ``` ID | FAIRYTALE | MINIATURE | MIXED HEIRLOOM VARIETIES | PIE TYPE ----|-----------|-----------|--------------------------|---------- 70 | 0 | 0 | 0 | 1 71 | 0 | 0 | 0 | 1 ... | ... | ... | ... | ... 1738 | 0 | 1 | 0 | 0 1739 | 0 | 1 | 0 | 0 1740 | 0 | 1 | 0 | 0 1741 | 0 | 1 | 0 | 0 1742 | 0 | 1 | 0 | 0 For å trene lineær regresjon ved bruk av one-hot enkodet sort som input, trenger vi bare å initialisere `X` og `y`-dataene korrekt: ```python X = pd.get_dummies(new_pumpkins['Variety']) y = new_pumpkins['Price'] ``` Resten av koden er den samme som vi brukte ovenfor for å trene lineær regresjon. Hvis du prøver det, vil du se at den gjennomsnittlige kvadratiske feilen er omtrent den samme, men vi får en mye høyere determinasjonskoeffisient (~77 %). For å få enda mer nøyaktige prediksjoner kan vi ta flere kategoriske funksjoner i betraktning, samt numeriske funksjoner, som `Month` eller `DayOfYear`. For å få én stor funksjonsmatrise kan vi bruke `join`: ```python X = pd.get_dummies(new_pumpkins['Variety']) \ .join(new_pumpkins['Month']) \ .join(pd.get_dummies(new_pumpkins['City'])) \ .join(pd.get_dummies(new_pumpkins['Package'])) y = new_pumpkins['Price'] ``` Her tar vi også hensyn til `City` og `Package`-type, som gir oss MSE 2,84 (10 %) og determinasjon 0,94! ## Alt samlet For å lage den beste modellen kan vi bruke kombinerte (one-hot enkodede kategoriske + numeriske) data fra eksempelet ovenfor sammen med polynomisk regresjon. Her er den komplette koden for enkelhets skyld: ```python # set up training data X = pd.get_dummies(new_pumpkins['Variety']) \ .join(new_pumpkins['Month']) \ .join(pd.get_dummies(new_pumpkins['City'])) \ .join(pd.get_dummies(new_pumpkins['Package'])) y = new_pumpkins['Price'] # make train-test split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) # setup and train the pipeline pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression()) pipeline.fit(X_train,y_train) # predict results for test data pred = pipeline.predict(X_test) # calculate MSE and determination mse = np.sqrt(mean_squared_error(y_test,pred)) print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)') score = pipeline.score(X_train,y_train) print('Model determination: ', score) ``` Dette bør gi oss den beste determinasjonskoeffisienten på nesten 97 %, og MSE=2,23 (~8 % prediksjonsfeil). | Modell | MSE | Determinasjon | |--------|-----|---------------| | `DayOfYear` Lineær | 2,77 (17,2 %) | 0,07 | | `DayOfYear` Polynomisk | 2,73 (17,0 %) | 0,08 | | `Variety` Lineær | 5,24 (19,7 %) | 0,77 | | Alle funksjoner Lineær | 2,84 (10,5 %) | 0,94 | | Alle funksjoner Polynomisk | 2,23 (8,25 %) | 0,97 | 🏆 Bra jobbet! Du har laget fire regresjonsmodeller i én leksjon, og forbedret modellkvaliteten til 97 %. I den siste delen om regresjon vil du lære om logistisk regresjon for å bestemme kategorier. --- ## 🚀Utfordring Test flere forskjellige variabler i denne notatboken for å se hvordan korrelasjon samsvarer med modellens nøyaktighet. ## [Quiz etter forelesning](https://ff-quizzes.netlify.app/en/ml/) ## Gjennomgang og selvstudium I denne leksjonen lærte vi om lineær regresjon. Det finnes andre viktige typer regresjon. Les om Stepwise, Ridge, Lasso og Elasticnet-teknikker. Et godt kurs for å lære mer er [Stanford Statistical Learning course](https://online.stanford.edu/courses/sohs-ystatslearning-statistical-learning). ## Oppgave [Bygg en modell](assignment.md) --- **Ansvarsfraskrivelse**: Dette dokumentet er oversatt ved hjelp av AI-oversettelsestjenesten [Co-op Translator](https://github.com/Azure/co-op-translator). Selv om vi tilstreber nøyaktighet, vennligst vær oppmerksom på at automatiske oversettelser kan inneholde feil eller unøyaktigheter. Det originale dokumentet på sitt opprinnelige språk bør anses som den autoritative kilden. For kritisk informasjon anbefales profesjonell menneskelig oversettelse. Vi er ikke ansvarlige for eventuelle misforståelser eller feiltolkninger som oppstår ved bruk av denne oversettelsen.