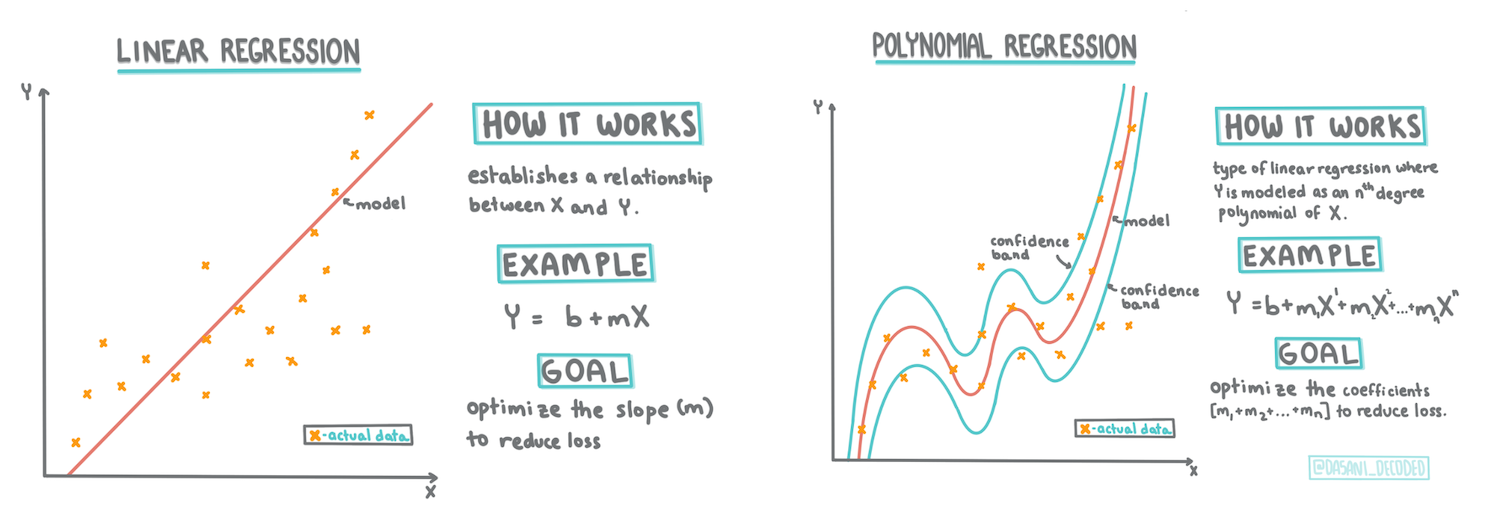
# Scikit-learn प्रयोग गरेर रिग्रेशन मोडेल बनाउने: चार तरिकामा रिग्रेशन  > इन्फोग्राफिक: [Dasani Madipalli](https://twitter.com/dasani_decoded) ## [पाठ अघि क्विज](https://ff-quizzes.netlify.app/en/ml/) > ### [यो पाठ R मा उपलब्ध छ!](../../../../2-Regression/3-Linear/solution/R/lesson_3.html) ### परिचय अहिलेसम्म तपाईंले रिग्रेशन के हो भनेर बुझ्न कद्दूको मूल्य निर्धारण डेटासेटको नमूना डाटाको साथ अन्वेषण गर्नुभएको छ, जुन हामीले यस पाठभरि प्रयोग गर्नेछौं। तपाईंले यसलाई Matplotlib प्रयोग गरेर दृश्यात्मक रूपमा पनि हेर्नुभएको छ। अब तपाईं ML को लागि रिग्रेशनमा गहिरो रूपमा जान तयार हुनुहुन्छ। दृश्यात्मकता डाटालाई बुझ्न मद्दत गर्दछ, तर मेसिन लर्निङको वास्तविक शक्ति _मोडेल प्रशिक्षण_ बाट आउँछ। मोडेलहरू ऐतिहासिक डाटामा प्रशिक्षित गरिन्छन् ताकि डाटाको निर्भरता स्वचालित रूपमा समात्न सकियोस्, र तिनीहरूले नयाँ डाटाको लागि परिणामहरू भविष्यवाणी गर्न अनुमति दिन्छन्, जुन मोडेलले पहिले देखेको छैन। यस पाठमा, तपाईं दुई प्रकारका रिग्रेशनबारे थप जान्नेछ: _साधारण रेखीय रिग्रेशन_ र _बहुपद रिग्रेशन_, साथै यी प्रविधिहरूको आधारभूत गणित। यी मोडेलहरूले हामीलाई विभिन्न इनपुट डाटाको आधारमा कद्दूको मूल्य भविष्यवाणी गर्न अनुमति दिनेछन्। [](https://youtu.be/CRxFT8oTDMg "मेसिन लर्निङका लागि शुरुआती - रेखीय रिग्रेशन बुझ्दै") > 🎥 माथिको छवि क्लिक गरेर रेखीय रिग्रेशनको छोटो भिडियो अवलोकन हेर्नुहोस्। > यस पाठ्यक्रमभरि, हामी न्यूनतम गणितीय ज्ञानलाई मान्यता दिन्छौं, र अन्य क्षेत्रबाट आएका विद्यार्थीहरूको लागि यसलाई पहुँचयोग्य बनाउन प्रयास गर्छौं। नोटहरू, 🧮 गणितीय संकेतहरू, रेखाचित्रहरू, र अन्य सिकाइ उपकरणहरूको लागि ध्यान दिनुहोस्। ### पूर्वआवश्यकता तपाईंले अहिले सम्म कद्दूको डाटाको संरचनासँग परिचित हुनुहुन्छ जुन हामी अध्ययन गर्दैछौं। यो पाठको _notebook.ipynb_ फाइलमा पूर्वलोड गरिएको र सफा गरिएको छ। फाइलमा, कद्दूको मूल्य प्रति बुशल नयाँ डाटाफ्रेममा देखाइएको छ। सुनिश्चित गर्नुहोस् कि तपाईं यी नोटबुकहरू Visual Studio Code मा चलाउन सक्नुहुन्छ। ### तयारी याद दिलाउनका लागि, तपाईं यो डाटा लोड गर्दै हुनुहुन्छ ताकि यसबाट प्रश्न सोध्न सकियोस्। - कद्दू किन्ने उत्तम समय कहिले हो? - सानो कद्दूको केसको मूल्य कति अपेक्षा गर्न सकिन्छ? - म तिनीहरूलाई आधा-बुशल टोकरीमा किन्ने कि 1 1/9 बुशल बक्समा? आउनुहोस्, यस डाटामा अझै गहिरो अध्ययन गरौं। पछिल्लो पाठमा, तपाईंले Pandas डाटाफ्रेम सिर्जना गर्नुभयो र मूल डेटासेटको भागसँग यसलाई भर्नुभयो, बुशलद्वारा मूल्यलाई मानकीकरण गर्दै। तर, त्यसो गर्दा, तपाईंले केवल लगभग 400 डाटाप्वाइन्टहरू मात्र संकलन गर्न सक्नुभयो र केवल शरद ऋतु महिनाहरूको लागि। यस पाठको साथमा रहेको नोटबुकमा पूर्वलोड गरिएको डाटालाई हेर्नुहोस्। डाटा पूर्वलोड गरिएको छ र प्रारम्भिक स्क्याटरप्लट चार्ट गरिएको छ ताकि महिनाको डाटा देखाउन सकियोस्। सायद हामी यस डाटाको प्रकृतिबारे अझै धेरै विवरण प्राप्त गर्न सक्छौं यदि यसलाई अझ सफा गरियो भने। ## रेखीय रिग्रेशन रेखा Lesson 1 मा तपाईंले सिक्नुभएको अनुसार, रेखीय रिग्रेशन अभ्यासको लक्ष्य एउटा रेखा प्लट गर्न सक्षम हुनु हो: - **चरहरूको सम्बन्ध देखाउनुहोस्**। चरहरू बीचको सम्बन्ध देखाउनुहोस् - **भविष्यवाणी गर्नुहोस्**। नयाँ डाटाप्वाइन्ट उक्त रेखासँगको सम्बन्धमा कहाँ पर्नेछ भन्ने सटीक भविष्यवाणी गर्नुहोस्। यो **Least-Squares Regression** को लागि सामान्य हो कि यस प्रकारको रेखा कोरियोस्। 'least-squares' शब्दको अर्थ हो कि रिग्रेशन रेखाको वरिपरिका सबै डाटाप्वाइन्टहरू वर्गाकार गरिन्छ र त्यसपछि जोडिन्छ। आदर्श रूपमा, अन्तिम योग यथासम्भव सानो हुनुपर्छ, किनभने हामी कम त्रुटिहरू, वा `least-squares` चाहन्छौं। हामी यसो गर्छौं किनभने हामी चाहन्छौं कि हाम्रो सबै डाटाप्वाइन्टहरूको सँग्लित दूरी कम भएको मोडेल बनोस्। हामीले तिनीहरूलाई वर्गाकार गरेर जोड्छौं किनभने हामी यसको परिमाणमा चासो राख्छौं, यसको दिशा होइन। > **🧮 गणित देखाउनुहोस्** > > यो रेखा, जसलाई _सबैभन्दा राम्रो फिटको रेखा_ भनिन्छ, [एक समीकरण](https://en.wikipedia.org/wiki/Simple_linear_regression) द्वारा व्यक्त गर्न सकिन्छ: > > ``` > Y = a + bX > ``` > > `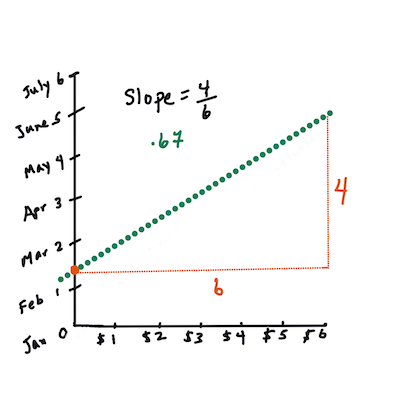X` 'व्याख्यात्मक चर' हो। `Y` 'निर्भर चर' हो। रेखाको ढलान `b` हो र `a` y-अवरोध हो, जसले `X = 0` हुँदा `Y` को मानलाई जनाउँछ। > > > > पहिलो, ढलान `b` गणना गर्नुहोस्। इन्फोग्राफिक: [Jen Looper](https://twitter.com/jenlooper) > > अर्को शब्दमा, र हाम्रो कद्दू डाटाको मूल प्रश्नलाई सन्दर्भ गर्दै: "महिनाद्वारा प्रति बुशल कद्दूको मूल्य भविष्यवाणी गर्नुहोस्", `X` मूल्यलाई जनाउँछ र `Y` बिक्रीको महिनालाई जनाउँछ। > > > > `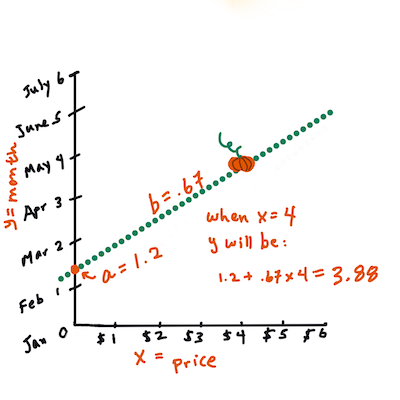Y` को मान गणना गर्नुहोस्। यदि तपाईं लगभग $4 तिर्दै हुनुहुन्छ भने, यो अप्रिल हुनुपर्छ! इन्फोग्राफिक: [Jen Looper](https://twitter.com/jenlooper) > > रेखाको ढलान गणना गर्ने गणित, जुन अवरोधमा पनि निर्भर गर्दछ, `X = 0` हुँदा `Y` कहाँ स्थित छ भनेर देखाउनुपर्छ। > > तपाईंले यी मानहरूको गणना गर्ने विधि [Math is Fun](https://www.mathsisfun.com/data/least-squares-regression.html) वेबसाइटमा अवलोकन गर्न सक्नुहुन्छ। [यो Least-squares calculator](https://www.mathsisfun.com/data/least-squares-calculator.html) पनि भ्रमण गर्नुहोस् ताकि संख्याहरूको मानले रेखालाई कसरी प्रभाव पार्छ हेर्न सकियोस्। ## सम्बन्ध अर्को शब्द बुझ्नुपर्ने भनेको **Correlation Coefficient** हो, जुन दिइएको X र Y चरहरू बीचको सम्बन्ध हो। स्क्याटरप्लट प्रयोग गरेर, तपाईंले यो गुणांकलाई छिटो दृश्यात्मक रूपमा हेर्न सक्नुहुन्छ। यदि प्लटमा डाटाप्वाइन्टहरू एक सुन्दर रेखामा फैलिएका छन् भने उच्च सम्बन्ध हुन्छ, तर यदि प्लटमा डाटाप्वाइन्टहरू X र Y बीचमा जताततै फैलिएका छन् भने कम सम्बन्ध हुन्छ। एक राम्रो रेखीय रिग्रेशन मोडेल भनेको उच्च (1 नजिक, 0 भन्दा टाढा) सम्बन्ध गुणांक भएको मोडेल हो, Least-Squares Regression विधि प्रयोग गरेर रिग्रेशन रेखासँग। ✅ यस पाठसँगको नोटबुक चलाउनुहोस् र महिना र मूल्यको स्क्याटरप्लट हेर्नुहोस्। कद्दू बिक्रीको लागि महिना र मूल्यको डाटा स्क्याटरप्लटको दृश्यात्मक व्याख्याको आधारमा उच्च वा कम सम्बन्ध देखिन्छ? यदि तपाईं `महिना` को सट्टा *वर्षको दिन* (जस्तै, वर्षको सुरुबाट दिनहरूको संख्या) प्रयोग गर्नुहुन्छ भने के यो परिवर्तन हुन्छ? तलको कोडमा, हामी मान्छौं कि हामीले डाटालाई सफा गरिसकेका छौं, र `new_pumpkins` नामक डाटाफ्रेम प्राप्त गरेका छौं, निम्नानुसार: ID | महिना | वर्षको दिन | प्रकार | सहर | प्याकेज | न्यूनतम मूल्य | उच्चतम मूल्य | मूल्य ---|-------|-----------|---------|------|---------|-----------|------------|------- 70 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 बुशल कार्टन | 15.0 | 15.0 | 13.636364 71 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 बुशल कार्टन | 18.0 | 18.0 | 16.363636 72 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 बुशल कार्टन | 18.0 | 18.0 | 16.363636 73 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 बुशल कार्टन | 17.0 | 17.0 | 15.454545 74 | 10 | 281 | PIE TYPE | BALTIMORE | 1 1/9 बुशल कार्टन | 15.0 | 15.0 | 13.636364 > डाटा सफा गर्ने कोड [`notebook.ipynb`](../../../../2-Regression/3-Linear/notebook.ipynb) मा उपलब्ध छ। हामीले अघिल्लो पाठमा जस्तै सफा गर्ने चरणहरू पूरा गरेका छौं, र निम्न अभिव्यक्तिको प्रयोग गरेर `DayOfYear` स्तम्भ गणना गरेका छौं: ```python day_of_year = pd.to_datetime(pumpkins['Date']).apply(lambda dt: (dt-datetime(dt.year,1,1)).days) ``` अब तपाईंले रेखीय रिग्रेशनको गणितको समझ पाउनुभएको छ, आउनुहोस् रिग्रेशन मोडेल बनाऔं ताकि हामी भविष्यवाणी गर्न सकौं कि कद्दूको प्याकेजको मूल्य कुनमा सबैभन्दा राम्रो हुनेछ। छुट्टीको कद्दूको बगैंचाको लागि कद्दू किन्ने कोहीले कद्दू प्याकेजहरूको खरीदलाई अनुकूलित गर्न यो जानकारी चाहन सक्छ। ## सम्बन्ध खोज्दै [](https://youtu.be/uoRq-lW2eQo "मेसिन लर्निङका लागि शुरुआती - सम्बन्ध खोज्दै: रेखीय रिग्रेशनको कुञ्जी") > 🎥 माथिको छवि क्लिक गरेर सम्बन्धको छोटो भिडियो अवलोकन हेर्नुहोस्। पछिल्लो पाठबाट तपाईंले सम्भवतः देख्नुभएको छ कि विभिन्न महिनाहरूको लागि औसत मूल्य यस प्रकार देखिन्छ: यसले सुझाव दिन्छ कि केही सम्बन्ध हुनुपर्छ, र हामी `महिना` र `मूल्य` बीचको सम्बन्ध भविष्यवाणी गर्न, वा `DayOfYear` र `मूल्य` बीचको सम्बन्ध भविष्यवाणी गर्न रेखीय रिग्रेशन मोडेल प्रशिक्षण गर्न प्रयास गर्न सक्छौं। यहाँ स्क्याटरप्लट छ जसले पछिल्लो सम्बन्ध देखाउँछ: आउनुहोस् `corr` फंक्शन प्रयोग गरेर सम्बन्ध छ कि छैन हेर्नुहोस्: ```python print(new_pumpkins['Month'].corr(new_pumpkins['Price'])) print(new_pumpkins['DayOfYear'].corr(new_pumpkins['Price'])) ``` यो देखिन्छ कि सम्बन्ध धेरै सानो छ, `महिना` द्वारा -0.15 र `DayOfMonth` द्वारा -0.17, तर अर्को महत्त्वपूर्ण सम्बन्ध हुन सक्छ। यस्तो देखिन्छ कि विभिन्न कद्दू प्रकारहरूका लागि मूल्यका विभिन्न समूहहरू छन्। यस परिकल्पनालाई पुष्टि गर्न, आउनुहोस् प्रत्येक कद्दूको प्रकारलाई फरक रंगमा प्लट गरौं। `scatter` प्लटिङ फंक्शनमा `ax` प्यारामिटर पास गरेर हामी सबै बिन्दुहरू एउटै ग्राफमा प्लट गर्न सक्छौं: ```python ax=None colors = ['red','blue','green','yellow'] for i,var in enumerate(new_pumpkins['Variety'].unique()): df = new_pumpkins[new_pumpkins['Variety']==var] ax = df.plot.scatter('DayOfYear','Price',ax=ax,c=colors[i],label=var) ``` हाम्रो अनुसन्धानले सुझाव दिन्छ कि प्रकारले वास्तविक बिक्री मितिभन्दा समग्र मूल्यमा बढी प्रभाव पार्छ। हामीले यो बार ग्राफको साथ देख्न सक्छौं: ```python new_pumpkins.groupby('Variety')['Price'].mean().plot(kind='bar') ``` आउनुहोस् अहिलेको लागि केवल एक कद्दू प्रकार, 'pie type', मा ध्यान केन्द्रित गरौं, र हेर्नुहोस् कि मितिले मूल्यमा कस्तो प्रभाव पार्छ: ```python pie_pumpkins = new_pumpkins[new_pumpkins['Variety']=='PIE TYPE'] pie_pumpkins.plot.scatter('DayOfYear','Price') ``` यदि हामी अहिले `corr` फंक्शन प्रयोग गरेर `मूल्य` र `DayOfYear` बीचको सम्बन्ध गणना गर्छौं भने, हामीले `-0.27` जस्तो केही प्राप्त गर्नेछौं - जसको अर्थ भविष्यवाणी मोडेल प्रशिक्षण गर्नुको अर्थ छ। > रेखीय रिग्रेशन मोडेल प्रशिक्षण गर्नु अघि, यो सुनिश्चित गर्नु महत्त्वपूर्ण छ कि हाम्रो डाटा सफा छ। रेखीय रिग्रेशनले हराएका मानहरूसँग राम्रोसँग काम गर्दैन, त्यसैले सबै खाली कोषहरू हटाउनु उचित हुन्छ: ```python pie_pumpkins.dropna(inplace=True) pie_pumpkins.info() ``` अर्को दृष्टिकोण भनेको ती खाली मानहरूलाई सम्बन्धित स्तम्भबाट औसत मानहरूद्वारा भरिदिनु हो। ## साधारण रेखीय रिग्रेशन [](https://youtu.be/e4c_UP2fSjg "मेसिन लर्निङका लागि शुरुआती - Scikit-learn प्रयोग गरेर रेखीय र बहुपद रिग्रेशन") > 🎥 माथिको छवि क्लिक गरेर रेखीय र बहुपद रिग्रेशनको छोटो भिडियो अवलोकन हेर्नुहोस्। हाम्रो रेखीय रिग्रेशन मोडेल प्रशिक्षण गर्न, हामी **Scikit-learn** लाइब्रेरी प्रयोग गर्नेछौं। ```python from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error from sklearn.model_selection import train_test_split ``` हामी इनपुट मानहरू (features) र अपेक्षित आउटपुट (label) लाई अलग-अलग numpy arrays मा विभाजन गरेर सुरु गर्छौं: ```python X = pie_pumpkins['DayOfYear'].to_numpy().reshape(-1,1) y = pie_pumpkins['Price'] ``` > ध्यान दिनुहोस् कि हामीले इनपुट डाटामा `reshape` प्रदर्शन गर्नुपर्‍यो ताकि रेखीय रिग्रेशन प्याकेजले यसलाई सही रूपमा बुझ्न सकियोस्। रेखीय रिग्रेशनले इनपुटको रूपमा 2D-array अपेक्षा गर्दछ, जहाँ array को प्रत्येक पङ्क्ति इनपुट features को भेक्टरसँग मेल खान्छ। हाम्रो केसमा, किनभने हामीसँग केवल एक इनपुट छ - हामीलाई आकार N×1 भएको array चाहिन्छ, जहाँ N डेटासेटको आकार हो। त्यसपछि, हामीले डाटालाई ट्रेन र टेस्ट डेटासेटहरूमा विभाजन गर्नुपर्छ ताकि प्रशिक्षण पछि हाम्रो मोडेललाई मान्य गर्न सकियोस्: ```python X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) ``` अन्ततः, वास्तविक रेखीय रिग्रेशन मोडेल प्रशिक्षण गर्न केवल दुई लाइन कोड लाग्छ। हामी `LinearRegression` वस्तु परिभाषित गर्छौं, र `fit` विधि प्रयोग गरेर यसलाई हाम्रो डाटामा फिट गर्छौं: ```python lin_reg = LinearRegression() lin_reg.fit(X_train,y_train) ``` `LinearRegression` वस्तु `fit`-पश्चात् रिग्रेशनका सबै गुणांकहरू समावेश गर्दछ, जसलाई `.coef_` प्रोपर्टी प्रयोग गरेर पहुँच गर्न सकिन्छ। हाम्रो केसमा, केवल एक गुणांक छ, जुन `-0.017` को वरिपरि हुनुपर्छ। यसको अर्थ मूल्य समयसँगै थोरै घट्छ, तर धेरै होइन, लगभग प्रति दिन 2 सेन्ट। हामी रिग्रेशनको Y-अक्षसँगको intersection बिन्दु `lin_reg.intercept_` प्रयोग गरेर पनि पहुँच गर्न सक्छौं - यो हाम्रो केसमा लगभग `21` हुनेछ, जसले वर्षको सुरुमा मूल्यलाई संकेत गर्दछ। हाम्रो मोडेल कति सटीक छ हेर्नको लागि, हामी टेस्ट डेटासेटमा मूल्यहरू भविष्यवाणी गर्न सक्छौं, र त्यसपछि हाम्रो भविष्यवाणीहरू अपेक्षित मानहरूसँग कति नजिक छन् मापन गर्न सक्छौं। यो mean square error (MSE) मेट्रिक्स प्रयोग गरेर गर्न सकिन्छ, जुन अपेक्षित र भविष्यवाणी गरिएको मानहरू बीचको सबै वर्गाकार भिन्नताहरूको औसत हो। ```python pred = lin_reg.predict(X_test) mse = np.sqrt(mean_squared_error(y_test,pred)) print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)') ``` हाम्रो त्रुटि लगभग २ बिन्दुमा देखिन्छ, जुन ~१७% हो। यो धेरै राम्रो छैन। मोडेलको गुणस्तरको अर्को सूचक **निर्धारण गुणांक** हो, जसलाई यसरी प्राप्त गर्न सकिन्छ: ```python score = lin_reg.score(X_train,y_train) print('Model determination: ', score) ``` यदि मान ० छ भने यसको अर्थ मोडेलले इनपुट डाटालाई ध्यानमा राख्दैन, र *सबभन्दा खराब रेखीय भविष्यवक्ता* को रूपमा कार्य गर्दछ, जुन परिणामको औसत मान मात्र हो। मान १ भएमा हामी सबै अपेक्षित नतिजाहरू पूर्ण रूपमा भविष्यवाणी गर्न सक्छौं। हाम्रो अवस्थामा, निर्धारण गुणांक लगभग ०.०६ छ, जुन धेरै कम छ। हामी परीक्षण डाटा र रिग्रेसन रेखालाई सँगै प्लट गर्न सक्छौं ताकि हाम्रो अवस्थामा रिग्रेसन कसरी काम गर्छ भन्ने राम्रोसँग देख्न सकियोस्: ```python plt.scatter(X_test,y_test) plt.plot(X_test,pred) ``` ## बहुपद रिग्रेसन रेखीय रिग्रेसनको अर्को प्रकार बहुपद रिग्रेसन हो। कहिलेकाहीँ चरहरू बीच रेखीय सम्बन्ध हुन्छ - जस्तै, कद्दूको मात्रा ठूलो भएमा मूल्य उच्च हुन्छ - तर कहिलेकाहीँ यी सम्बन्धहरू समतल वा सीधा रेखाको रूपमा प्लट गर्न सकिँदैन। ✅ यहाँ [केही थप उदाहरणहरू](https://online.stat.psu.edu/stat501/lesson/9/9.8) छन् जसले बहुपद रिग्रेसन प्रयोग गर्न सक्ने डाटा देखाउँछ। मिति र मूल्य बीचको सम्बन्धलाई फेरि हेर्नुहोस्। के यो स्क्याटरप्लट सीधा रेखाले विश्लेषण गर्नुपर्छ जस्तो देखिन्छ? के मूल्यहरू परिवर्तन हुन सक्दैनन्? यस अवस्थामा, तपाईं बहुपद रिग्रेसन प्रयास गर्न सक्नुहुन्छ। ✅ बहुपदहरू गणितीय अभिव्यक्तिहरू हुन् जसमा एक वा बढी चर र गुणांकहरू समावेश हुन सक्छन्। बहुपद रिग्रेसनले गैर-रेखीय डाटालाई राम्रोसँग फिट गर्न घुमाउरो रेखा सिर्जना गर्छ। हाम्रो अवस्थामा, यदि हामी इनपुट डाटामा वर्गाकार `DayOfYear` चर समावेश गर्छौं भने, हामी हाम्रो डाटालाई पराबोलिक वक्रसँग फिट गर्न सक्षम हुनेछौं, जसको न्यूनतम वर्षको निश्चित बिन्दुमा हुनेछ। Scikit-learn ले विभिन्न डाटा प्रशोधन चरणहरूलाई सँगै संयोजन गर्न उपयोगी [पाइपलाइन API](https://scikit-learn.org/stable/modules/generated/sklearn.pipeline.make_pipeline.html?highlight=pipeline#sklearn.pipeline.make_pipeline) समावेश गर्दछ। **पाइपलाइन** **अनुमानकर्ताहरू** को श्रृंखला हो। हाम्रो अवस्थामा, हामी एक पाइपलाइन सिर्जना गर्नेछौं जसले पहिलो बहुपद विशेषताहरूलाई हाम्रो मोडेलमा थप्छ, र त्यसपछि रिग्रेसनलाई प्रशिक्षण दिन्छ: ```python from sklearn.preprocessing import PolynomialFeatures from sklearn.pipeline import make_pipeline pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression()) pipeline.fit(X_train,y_train) ``` `PolynomialFeatures(2)` प्रयोग गर्दा यसको अर्थ इनपुट डाटाबाट सबै दोस्रो-डिग्री बहुपदहरू समावेश हुनेछ। हाम्रो अवस्थामा यसको मतलब केवल `DayOfYear`² हुनेछ, तर दुई इनपुट चरहरू X र Y दिँदा, यसले X², XY र Y² थप्नेछ। यदि हामी चाहन्छौं भने उच्च डिग्री बहुपदहरू पनि प्रयोग गर्न सक्छौं। पाइपलाइनहरू मूल `LinearRegression` वस्तुको जस्तै तरिकामा प्रयोग गर्न सकिन्छ, अर्थात् हामी पाइपलाइनलाई `fit` गर्न सक्छौं, र त्यसपछि भविष्यवाणी परिणामहरू प्राप्त गर्न `predict` प्रयोग गर्न सक्छौं। यहाँ परीक्षण डाटा र अनुमान वक्र देखाउने ग्राफ छ: बहुपद रिग्रेसन प्रयोग गर्दा, हामी थोरै कम MSE र उच्च निर्धारण प्राप्त गर्न सक्छौं, तर धेरै महत्त्वपूर्ण रूपमा होइन। हामीले अन्य विशेषताहरूलाई ध्यानमा राख्न आवश्यक छ! > तपाईं देख्न सक्नुहुन्छ कि न्यूनतम कद्दू मूल्यहरू हलोविनको वरिपरि देखिन्छ। तपाईं यसलाई कसरी व्याख्या गर्न सक्नुहुन्छ? 🎃 बधाई छ, तपाईंले पाई कद्दूको मूल्य भविष्यवाणी गर्न मद्दत गर्ने मोडेल सिर्जना गर्नुभयो। तपाईं सम्भवतः सबै कद्दू प्रकारहरूको लागि समान प्रक्रिया दोहोर्याउन सक्नुहुन्छ, तर त्यो थकाउने हुनेछ। अब सिकौं कि कसरी हाम्रो मोडेलमा कद्दूको विविधतालाई ध्यानमा राख्ने! ## श्रेणीगत विशेषताहरू आदर्श संसारमा, हामी एउटै मोडेल प्रयोग गरेर विभिन्न कद्दू प्रकारहरूको मूल्य भविष्यवाणी गर्न सक्षम हुन चाहन्छौं। तर, `Variety` स्तम्भ `Month` जस्ता स्तम्भहरू भन्दा केही फरक छ, किनभने यसमा गैर-संख्यात्मक मानहरू समावेश छन्। यस्ता स्तम्भहरूलाई **श्रेणीगत** भनिन्छ। [](https://youtu.be/DYGliioIAE0 "शुरुआतीहरूको लागि ML - श्रेणीगत विशेषताहरूको साथ रेखीय रिग्रेसन") > 🎥 माथिको छवि क्लिक गरेर श्रेणीगत विशेषताहरू प्रयोग गर्ने छोटो भिडियो अवलोकन हेर्नुहोस्। यहाँ तपाईं देख्न सक्नुहुन्छ कि औसत मूल्य विविधतामा कसरी निर्भर गर्दछ: विविधतालाई ध्यानमा राख्न, हामीले पहिले यसलाई संख्यात्मक रूपमा रूपान्तरण गर्न आवश्यक छ, वा **एन्कोड** गर्नुपर्छ। यसलाई गर्नका लागि केही तरिकाहरू छन्: * साधारण **संख्यात्मक एन्कोडिङ** ले विभिन्न विविधताहरूको तालिका बनाउनेछ, र त्यसपछि विविधताको नामलाई उक्त तालिकामा सूचकांकले प्रतिस्थापन गर्नेछ। यो रेखीय रिग्रेसनको लागि उत्तम विचार होइन, किनभने रेखीय रिग्रेसनले सूचकांकको वास्तविक संख्यात्मक मानलाई लिन्छ, र केही गुणांकले गुणा गरेर नतिजामा थप्छ। हाम्रो अवस्थामा, सूचकांक नम्बर र मूल्य बीचको सम्बन्ध स्पष्ट रूपमा गैर-रेखीय छ, भले पनि हामी सुनिश्चित गर्छौं कि सूचकांकहरू कुनै विशिष्ट तरिकामा क्रमबद्ध छन्। * **वन-हट एन्कोडिङ** ले `Variety` स्तम्भलाई ४ विभिन्न स्तम्भहरूले प्रतिस्थापन गर्नेछ, प्रत्येक विविधताको लागि एउटा। प्रत्येक स्तम्भले `१` समावेश गर्नेछ यदि सम्बन्धित पङ्क्ति दिइएको विविधताको हो भने, र `०` अन्यथा। यसको मतलब रेखीय रिग्रेसनमा चार गुणांकहरू हुनेछन्, प्रत्येक कद्दू विविधताको लागि, उक्त विशेष विविधताको लागि "सुरुवात मूल्य" (वा "थप मूल्य") को जिम्मेवार। तलको कोडले विविधतालाई वन-हट एन्कोड कसरी गर्न सकिन्छ देखाउँछ: ```python pd.get_dummies(new_pumpkins['Variety']) ``` ID | FAIRYTALE | MINIATURE | MIXED HEIRLOOM VARIETIES | PIE TYPE ----|-----------|-----------|--------------------------|---------- 70 | 0 | 0 | 0 | 1 71 | 0 | 0 | 0 | 1 ... | ... | ... | ... | ... 1738 | 0 | 1 | 0 | 0 1739 | 0 | 1 | 0 | 0 1740 | 0 | 1 | 0 | 0 1741 | 0 | 1 | 0 | 0 1742 | 0 | 1 | 0 | 0 वन-हट एन्कोड गरिएको विविधतालाई इनपुटको रूपमा प्रयोग गरेर रेखीय रिग्रेसन प्रशिक्षण गर्न, हामीले केवल `X` र `y` डाटालाई सही रूपमा आरम्भ गर्न आवश्यक छ: ```python X = pd.get_dummies(new_pumpkins['Variety']) y = new_pumpkins['Price'] ``` बाकी कोड माथि प्रयोग गरिएको रेखीय रिग्रेसन प्रशिक्षण गर्न प्रयोग गरिएको कोड जस्तै छ। यदि तपाईंले प्रयास गर्नुभयो भने, तपाईं देख्नुहुनेछ कि औसत वर्ग त्रुटि लगभग उस्तै छ, तर हामीले धेरै उच्च निर्धारण गुणांक (~७७%) प्राप्त गर्छौं। अझ सही भविष्यवाणीहरू प्राप्त गर्न, हामीले थप श्रेणीगत विशेषताहरू, साथै संख्यात्मक विशेषताहरू, जस्तै `Month` वा `DayOfYear` लाई ध्यानमा राख्न सक्छौं। विशेषताहरूको ठूलो एरे प्राप्त गर्न, हामी `join` प्रयोग गर्न सक्छौं: ```python X = pd.get_dummies(new_pumpkins['Variety']) \ .join(new_pumpkins['Month']) \ .join(pd.get_dummies(new_pumpkins['City'])) \ .join(pd.get_dummies(new_pumpkins['Package'])) y = new_pumpkins['Price'] ``` यहाँ हामीले `City` र `Package` प्रकारलाई पनि ध्यानमा राखेका छौं, जसले हामीलाई MSE २.८४ (१०%) र निर्धारण ०.९४ दिन्छ! ## सबैलाई सँगै राख्दै सर्वश्रेष्ठ मोडेल बनाउन, हामी माथिको उदाहरणबाट संयुक्त (वन-हट एन्कोड गरिएको श्रेणीगत + संख्यात्मक) डाटा बहुपद रिग्रेसनसँग प्रयोग गर्न सक्छौं। यहाँ तपाईंको सुविधाको लागि पूर्ण कोड छ: ```python # set up training data X = pd.get_dummies(new_pumpkins['Variety']) \ .join(new_pumpkins['Month']) \ .join(pd.get_dummies(new_pumpkins['City'])) \ .join(pd.get_dummies(new_pumpkins['Package'])) y = new_pumpkins['Price'] # make train-test split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) # setup and train the pipeline pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression()) pipeline.fit(X_train,y_train) # predict results for test data pred = pipeline.predict(X_test) # calculate MSE and determination mse = np.sqrt(mean_squared_error(y_test,pred)) print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)') score = pipeline.score(X_train,y_train) print('Model determination: ', score) ``` यसले हामीलाई लगभग ९७% निर्धारण गुणांक र MSE=२.२३ (~८% भविष्यवाणी त्रुटि) दिन्छ। | मोडेल | MSE | निर्धारण | |-------|-----|----------| | `DayOfYear` रेखीय | २.७७ (१७.२%) | ०.०७ | | `DayOfYear` बहुपद | २.७३ (१७.०%) | ०.०८ | | `Variety` रेखीय | ५.२४ (१९.७%) | ०.७७ | | सबै विशेषताहरू रेखीय | २.८४ (१०.५%) | ०.९४ | | सबै विशेषताहरू बहुपद | २.२३ (८.२५%) | ०.९७ | 🏆 राम्रो काम! तपाईंले एक पाठमा चार रिग्रेसन मोडेलहरू सिर्जना गर्नुभयो, र मोडेलको गुणस्तरलाई ९७% सम्म सुधार गर्नुभयो। रिग्रेसनको अन्तिम खण्डमा, तपाईंले श्रेणी निर्धारण गर्न लॉजिस्टिक रिग्रेसनको बारेमा सिक्नुहुनेछ। --- ## 🚀 चुनौती यस नोटबुकमा विभिन्न चरहरू परीक्षण गर्नुहोस् ताकि सम्बन्ध मोडेलको सटीकतासँग कसरी मेल खान्छ हेर्न सकियोस्। ## [पाठ-पछिको क्विज](https://ff-quizzes.netlify.app/en/ml/) ## समीक्षा र आत्म अध्ययन यस पाठमा हामीले रेखीय रिग्रेसनको बारेमा सिक्यौं। रिग्रेसनका अन्य महत्त्वपूर्ण प्रकारहरू छन्। Stepwise, Ridge, Lasso र Elasticnet प्रविधिहरूको बारेमा पढ्नुहोस्। थप जान्नको लागि राम्रो पाठ्यक्रम [स्ट्यानफोर्ड स्ट्याटिस्टिकल लर्निङ कोर्स](https://online.stanford.edu/courses/sohs-ystatslearning-statistical-learning) हो। ## असाइनमेन्ट [मोडेल बनाउनुहोस्](assignment.md) --- **अस्वीकरण**: यो दस्तावेज़ AI अनुवाद सेवा [Co-op Translator](https://github.com/Azure/co-op-translator) प्रयोग गरी अनुवाद गरिएको हो। हामी यथासम्भव सटीकता सुनिश्चित गर्न प्रयास गर्छौं, तर कृपया ध्यान दिनुहोस् कि स्वचालित अनुवादहरूमा त्रुटि वा अशुद्धता हुन सक्छ। यसको मूल भाषामा रहेको मूल दस्तावेज़लाई आधिकारिक स्रोत मानिनुपर्छ। महत्त्वपूर्ण जानकारीका लागि, व्यावसायिक मानव अनुवाद सिफारिस गरिन्छ। यस अनुवादको प्रयोगबाट उत्पन्न हुने कुनै पनि गलतफहमी वा गलत व्याख्याका लागि हामी जिम्मेवार हुने छैनौं।