# Scikit-learn ကို အသုံးပြု၍ Regression မော်ဒယ်တစ်ခု တည်ဆောက်ခြင်း: Regression လုပ်နည်း ၄ မျိုး
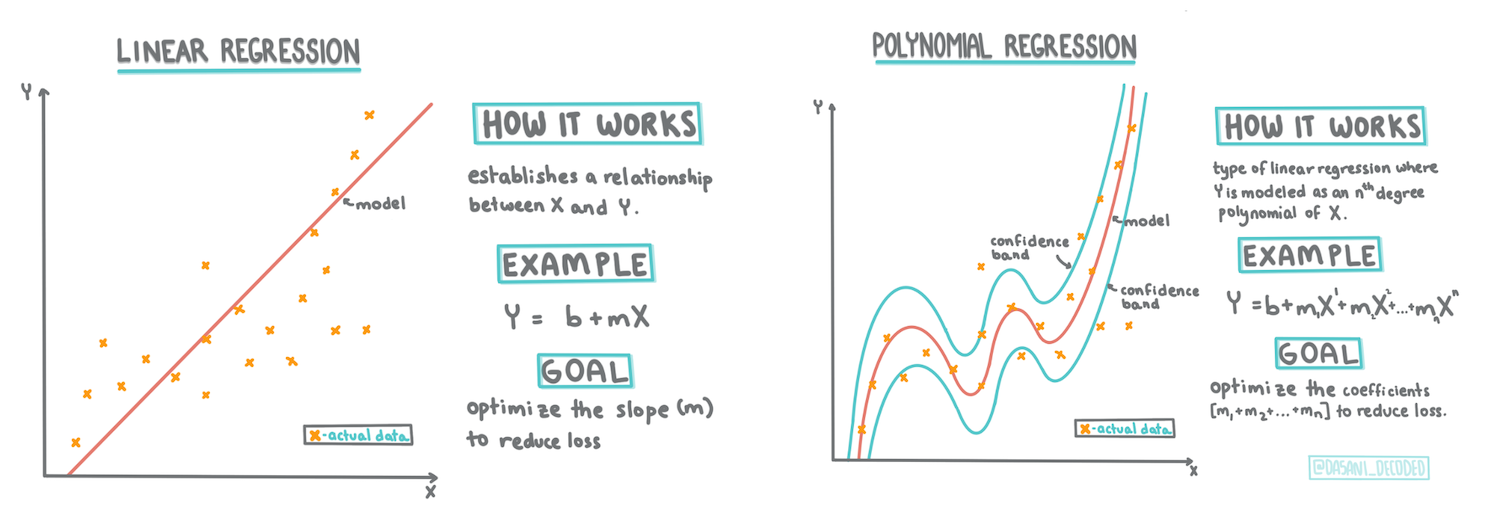
> Infographic by [Dasani Madipalli](https://twitter.com/dasani_decoded)
## [Pre-lecture quiz](https://ff-quizzes.netlify.app/en/ml/)
> ### [ဒီသင်ခန်းစာကို R မှာလည်းရနိုင်ပါတယ်!](../../../../2-Regression/3-Linear/solution/R/lesson_3.html)
### အကျဉ်းချုပ်
ယခင်အခန်းများတွင် Regression ဆိုတာဘာလဲဆိုတာကို သင် Pumpkin စျေးနှုန်း dataset ကို အသုံးပြု၍ လေ့လာခဲ့ပြီး Matplotlib ကို အသုံးပြု၍ visualization လုပ်ခဲ့ပါသည်။
အခုတော့ ML အတွက် Regression ကို ပိုမိုနက်နက်ရှိုင်းရှိုင်း လေ့လာရန် အဆင်သင့်ဖြစ်ပါပြီ။ Visualization က ဒေတာကို နားလည်စေသလို Machine Learning ရဲ့ အဓိကအားသာချက်ကတော့ _မော်ဒယ်များကို လေ့ကျင့်ခြင်း_ ဖြစ်ပါတယ်။ မော်ဒယ်များကို သမိုင်းကြောင်းဒေတာပေါ်မှာ လေ့ကျင့်ပြီး ဒေတာအချင်းချင်း ဆက်နွယ်မှုများကို အလိုအလျောက် ဖမ်းဆီးနိုင်စေပြီး မော်ဒယ်မမြင်ဖူးသေးတဲ့ ဒေတာအသစ်များအတွက် အကျိုးအမြတ်ကို ခန့်မှန်းနိုင်စေပါတယ်။
ဒီသင်ခန်းစာမှာ Regression အမျိုးအစား ၂ မျိုးကို ပိုမိုနက်နက်ရှိုင်းရှိုင်း လေ့လာပါမည်။ _အခြေခံ Linear Regression_ နှင့် _Polynomial Regression_ တို့ဖြစ်ပြီး ဒီနည်းလမ်းများရဲ့ သင်္ချာဆိုင်ရာ အခြေခံကိုလည်း လေ့လာပါမည်။ ဒီမော်ဒယ်များက Pumpkin စျေးနှုန်းကို input data အမျိုးမျိုးပေါ်မူတည်ပြီး ခန့်မှန်းနိုင်စေပါမည်။
[](https://youtu.be/CRxFT8oTDMg "ML for beginners - Understanding Linear Regression")
> 🎥 Linear Regression ရဲ့ အကျဉ်းချုပ်ကို ကြည့်ရန် အထက်ပါပုံကို နှိပ်ပါ။
> ဒီသင်ရိုးတစ်ခုလုံးမှာ သင်္ချာအပေါ် အနည်းငယ်သာ သိရှိမှုရှိသည်ဟု သတ်မှတ်ပြီး သင်္ချာကို အခြားနယ်ပယ်မှ ကျောင်းသားများလည်း နားလည်နိုင်စေရန် ရည်ရွယ်ထားပါသည်။ 🧮 မှတ်ချက်များ၊ အကြောင်းပြ callouts၊ ရှင်းလင်းပုံများနှင့် အခြားသင်ယူမှုကိရိယာများကို အသုံးပြုထားသည်။
### ကြိုတင်လိုအပ်ချက်
Pumpkin data ရဲ့ ဖွဲ့စည်းပုံကို ယခုအချိန်မှာ သင်နားလည်ပြီးဖြစ်ရမည်။ ဒီသင်ခန်းစာရဲ့ _notebook.ipynb_ ဖိုင်မှာ preloaded နှင့် pre-cleaned ဖြစ်ပြီး bushel တစ်ခုအတွက် Pumpkin စျေးနှုန်းကို အသစ်သော data frame မှာ ပြထားသည်။ Visual Studio Code ရဲ့ kernels တွင် ဒီ notebooks များကို run လုပ်နိုင်ရမည်။
### ပြင်ဆင်မှု
ဒီဒေတာကို load လုပ်ပြီး အမေးအဖြေများကို ရှာဖွေဖို့ သတိပြုပါ။
- Pumpkin ဝယ်ဖို့ အချိန်ကောင်းဆုံးက ဘယ်အချိန်လဲ?
- Miniature pumpkins တစ် case ရဲ့ စျေးနှုန်းကို ဘယ်လောက်ခန့်မှန်းနိုင်မလဲ?
- Half-bushel baskets နဲ့ 1 1/9 bushel box တစ်ခုကို ဘယ်ဟာကို ဝယ်သင့်လဲ?
ဒီဒေတာကို ဆက်လက် လေ့လာကြည့်ရအောင်။
ယခင်သင်ခန်းစာမှာ Pandas data frame တစ်ခုကို ဖန်တီးပြီး မူရင်း dataset ရဲ့ အစိတ်အပိုင်းတစ်ခုကို ထည့်သွင်းခဲ့သည်။ Pricing ကို bushel အတိုင်းအတာဖြင့် စံပြုခဲ့သည်။ ဒါပေမယ့် ၄၀၀ ခန့်သော datapoints ကိုသာ ရရှိခဲ့ပြီး ဆောင်းရာသီလများအတွက်သာ ရရှိခဲ့သည်။
ဒီသင်ခန်းစာရဲ့ notebook တွင် preloaded data ကို ကြည့်ပါ။ ဒေတာကို preloaded လုပ်ပြီး month data ကို scatterplot တစ်ခုအဖြစ် chart လုပ်ထားသည်။ ဒေတာရဲ့ nature ကို ပိုမိုသေချာစေရန် ပိုမိုသန့်စင်နိုင်မလားဆိုတာ ကြည့်ပါ။
## Linear Regression Line တစ်ခု
Lesson 1 မှာ သင်လေ့လာခဲ့သလို Linear Regression ရဲ့ ရည်ရွယ်ချက်ကတော့ လိုင်းတစ်ခုကို plot လုပ်နိုင်ရန် ဖြစ်သည်။
- **Variable ဆက်နွယ်မှုများကို ပြသရန်**။ Variable များအကြား ဆက်နွယ်မှုကို ပြသရန်
- **ခန့်မှန်းချက်များ ပြုလုပ်ရန်**။ Datapoint အသစ်တစ်ခုကို လိုင်းနှင့် ဆက်နွယ်မှုအပေါ် အတိအကျ ခန့်မှန်းရန်
**Least-Squares Regression** သုံးပြီး ဒီလိုင်းကို ရေးဆွဲသည်။ 'Least-squares' ဆိုတာက Regression လိုင်းကို ဝန်းရံထားသော datapoints များကို square လုပ်ပြီး ထည့်ပေါင်းခြင်းဖြစ်သည်။ အဆုံးသတ်ပေါင်းစုက အနည်းဆုံးဖြစ်ရမည်။ အမှားများနည်းသော `least-squares` ကို ရရှိရန် ဖြစ်သည်။
ဒါကို လုပ်ရတဲ့အကြောင်းကတော့ ဒေတာပွိုင့်များအားလုံးမှ cumulative distance အနည်းဆုံးဖြစ်သော လိုင်းတစ်ခုကို မော်ဒယ်ဖန်တီးလိုခြင်း ဖြစ်သည်။ ထို့အပြင် direction ကိုမဟုတ်ဘဲ magnitude ကိုသာ စိုးရိမ်သောကြောင့် term များကို square လုပ်ပြီး ထည့်ပေါင်းသည်။
> **🧮 သင်္ချာကို ပြပါ**
>
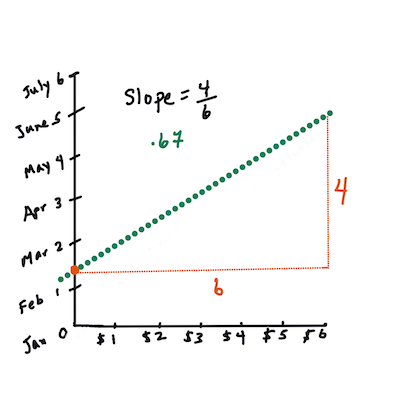
> ဒီလိုင်းကို _line of best fit_ ဟုခေါ်ပြီး [equation](https://en.wikipedia.org/wiki/Simple_linear_regression) ဖြင့် ဖော်ပြနိုင်သည်။
>
> ```
> Y = a + bX
> ```
>
> `X` က 'explanatory variable' ဖြစ်သည်။ `Y` က 'dependent variable' ဖြစ်သည်။ လိုင်းရဲ့ slope ကို `b` ဟုခေါ်ပြီး y-intercept ကို `a` ဟုခေါ်သည်။ `X = 0` ဖြစ်သောအခါ `Y` ရဲ့တန်ဖိုးကို ရည်ညွှန်းသည်။
>
>
>
> ပထမဆုံး slope `b` ကိုတွက်ပါ။ Infographic by [Jen Looper](https://twitter.com/jenlooper)
>
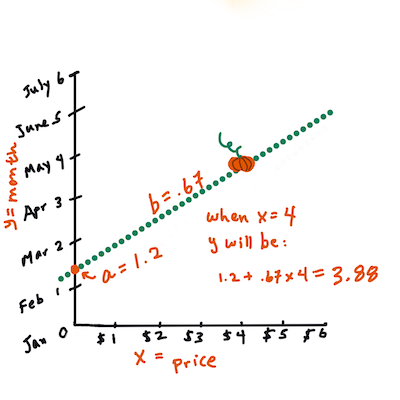
> Pumpkin data ရဲ့ မူရင်းမေးခွန်းကို ရည်ညွှန်းပါက "month အပေါ်မူတည်ပြီး bushel တစ်ခုအတွက် Pumpkin စျေးနှုန်းကို ခန့်မှန်းပါ" ဆိုသည်မှာ `X` က စျေးနှုန်းကို ရည်ညွှန်းပြီး `Y` က ရောင်းချသောလကို ရည်ညွှန်းသည်။
>
>
>
> `Y` ရဲ့တန်ဖိုးကိုတွက်ပါ။ $4 ဝန်းကျင်ပေးရမယ်ဆိုရင် April ဖြစ်နေလိမ့်မယ်! Infographic by [Jen Looper](https://twitter.com/jenlooper)
>
> လိုင်းရဲ့ slope ကိုတွက်ရန် သင်္ချာက intercept ကိုလည်း အခြေခံထားသည်။ `X = 0` ဖြစ်သောအခါ `Y` ရဲ့တည်နေရာကိုလည်း ထည့်သွင်းတွက်ချက်ထားသည်။
>
> ဒီတန်ဖိုးများရဲ့ လိုင်းကို ဘယ်လိုသတ်မှတ်ရမလဲဆိုတာကို [Math is Fun](https://www.mathsisfun.com/data/least-squares-regression.html) ဝဘ်ဆိုဒ်မှာ ကြည့်နိုင်သည်။ [Least-squares calculator](https://www.mathsisfun.com/data/least-squares-calculator.html) ကိုလည်း သုံးပြီး တန်ဖိုးများက လိုင်းကို ဘယ်လိုသက်ရောက်မှုရှိသလဲဆိုတာ ကြည့်နိုင်သည်။
## Correlation
နောက်ထပ်နားလည်ရမည့် term တစ်ခုကတော့ **Correlation Coefficient** ဖြစ်သည်။ X နှင့် Y variable များအကြား scatterplot ကို အသုံးပြု၍ Coefficient ကို မြန်မြန်ဆန်ဆန် visualization လုပ်နိုင်သည်။ Datapoints များကို တိကျသောလိုင်းတစ်ခုအတိုင်း scatter လုပ်ထားသော plot တွင် correlation မြင့်မားသည်။ X နှင့် Y အကြား scatter လုပ်ထားသော plot တွင် correlation နည်းပါမည်။
Linear Regression မော်ဒယ်က correlation coefficient မြင့်မားသော (၁ နီးစပ်ပြီး ၀ မနီးစပ်သော) Least-Squares Regression method နှင့် regression line ရှိရမည်။
✅ ဒီသင်ခန်းစာရဲ့ notebook ကို run လုပ်ပြီး Month နှင့် Price scatterplot ကိုကြည့်ပါ။ Pumpkin ရောင်းချမှုအတွက် Month နှင့် Price data တွေဟာ scatterplot အရ correlation မြင့်မားသလား၊ နိမ့်နားသလားဆိုတာ သင့် visual interpretation အရ သတ်မှတ်ပါ။ `Month` အစား *day of the year* (နှစ်အစမှစ၍ ရက်ပေါင်း) ကို အသုံးပြုပါက အဲဒီ correlation က ပြောင်းလဲသလား?
အောက်ပါ code မှာ သန့်စင်ပြီး data frame `new_pumpkins` ကို ရရှိထားသည်ဟု သတ်မှတ်ပါမည်။ အဲဒီ data frame က အောက်ပါအတိုင်းဖြစ်သည်။
ID | Month | DayOfYear | Variety | City | Package | Low Price | High Price | Price
---|-------|-----------|---------|------|---------|-----------|------------|-------
70 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 15.0 | 15.0 | 13.636364
71 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 18.0 | 18.0 | 16.363636
72 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 18.0 | 18.0 | 16.363636
73 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 17.0 | 17.0 | 15.454545
74 | 10 | 281 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 15.0 | 15.0 | 13.636364
> ဒီ data ကို သန့်စင်ရန် code ကို [`notebook.ipynb`](../../../../2-Regression/3-Linear/notebook.ipynb) တွင် ရရှိနိုင်သည်။ ယခင်သင်ခန်းစာတွင် လုပ်ခဲ့သည့် သန့်စင်ခြင်းအဆင့်များကို ပြုလုပ်ပြီး `DayOfYear` column ကို အောက်ပါ expression ကို အသုံးပြု၍ တွက်ချက်ထားသည်။
```python
day_of_year = pd.to_datetime(pumpkins['Date']).apply(lambda dt: (dt-datetime(dt.year,1,1)).days)
```
Linear Regression ရဲ့ သင်္ချာကို နားလည်ပြီးပြီဆိုရင် Pumpkin စျေးနှုန်းများကို ခန့်မှန်းနိုင်ရန် Regression မော်ဒယ်တစ်ခုကို ဖန်တီးကြည့်ရအောင်။ Holiday Pumpkin Patch အတွက် Pumpkin packages များကို optimize လုပ်ရန် ဝယ်ယူသူတစ်ဦးအတွက် ဒီအချက်အလက်များ အသုံးဝင်နိုင်ပါမည်။
## Correlation ရှာဖွေခြင်း
[](https://youtu.be/uoRq-lW2eQo "ML for beginners - Looking for Correlation: The Key to Linear Regression")
> 🎥 Correlation ရဲ့ အကျဉ်းချုပ်ကို ကြည့်ရန် အထက်ပါပုံကို နှိပ်ပါ။
ယခင်သင်ခန်းစာမှ သင်မြင်ခဲ့သည်မှာ အမျိုးမျိုးသောလများအတွက် အလယ်ပျဉ်စျေးနှုန်းသည် အောက်ပါအတိုင်းဖြစ်သည်။
ဒါက correlation ရှိနိုင်သည်ဟု အကြံပြုသည်။ Linear Regression မော်ဒယ်ကို `Month` နှင့် `Price` အကြား သို့မဟုတ် `DayOfYear` နှင့် `Price` အကြား ဆက်နွယ်မှုကို ခန့်မှန်းရန် လေ့ကျင့်ကြည့်နိုင်သည်။ အောက်ပါ scatter plot က `DayOfYear` နှင့် `Price` အကြား ဆက်နွယ်မှုကို ပြသည်။
`corr` function ကို အသုံးပြု၍ correlation ရှိမရှိ ကြည့်ရအောင်။
```python
print(new_pumpkins['Month'].corr(new_pumpkins['Price']))
print(new_pumpkins['DayOfYear'].corr(new_pumpkins['Price']))
```
`Month` အပေါ် correlation က -0.15 ဖြစ်ပြီး `DayOfYear` အပေါ် correlation က -0.17 ဖြစ်သည်။ ဒါပေမယ့် အခြားသော ဆက်နွယ်မှုတစ်ခုရှိနိုင်သည်။ Pumpkin အမျိုးအစားများနှင့် ဆက်နွယ်မှုရှိသည်ဟု ထင်ရသည်။ ဒီ hypothesis ကို အတည်ပြုရန် Pumpkin အမျိုးအစားတစ်ခုစီကို အရောင်ကွဲကွဲဖြင့် plot လုပ်ကြည့်ရအောင်။ `scatter` plotting function မှ `ax` parameter ကို အသုံးပြု၍ point အားလုံးကို graph တစ်ခုအပေါ် plot လုပ်နိုင်သည်။
```python
ax=None
colors = ['red','blue','green','yellow']
for i,var in enumerate(new_pumpkins['Variety'].unique()):
df = new_pumpkins[new_pumpkins['Variety']==var]
ax = df.plot.scatter('DayOfYear','Price',ax=ax,c=colors[i],label=var)
```
ကျွန်ုပ်တို့ရဲ့ စုံစမ်းမှုက variety က စျေးနှုန်းအပေါ် date ထက် ပိုမိုသက်ရောက်မှုရှိသည်ဟု အတည်ပြုသည်။ Bar graph ဖြင့်လည်း မြင်နိုင်သည်။
```python
new_pumpkins.groupby('Variety')['Price'].mean().plot(kind='bar')
```
ယခုအချိန်မှာ 'pie type' ဟုခေါ်သော Pumpkin အမျိုးအစားတစ်ခုကိုသာ အာရုံစိုက်ပြီး date ရဲ့ စျေးနှုန်းအပေါ် သက်ရောက်မှုကို ကြည့်ရအောင်။
```python
pie_pumpkins = new_pumpkins[new_pumpkins['Variety']=='PIE TYPE']
pie_pumpkins.plot.scatter('DayOfYear','Price')
```
`corr` function ကို အသုံးပြု၍ `Price` နှင့် `DayOfYear` အကြား correlation ကို တွက်ချက်ပါက `-0.27` ရရှိမည် - ဒါက predictive model တစ်ခုကို လေ့ကျင့်ခြင်း make sense ဖြစ်သည်ဟု ဆိုလိုသည်။
> Linear Regression မော်ဒယ်ကို လေ့ကျင့်မည်ဆိုရင် ဒေတာကို သန့်စင်ထားရန် အရေးကြီးသည်။ Linear Regression က missing values များနှင့် အလုပ်မလုပ်သင့်သောကြောင့် အလွတ်နေသော cell များကို ဖယ်ရှားရန် make sense ဖြစ်သည်။
```python
pie_pumpkins.dropna(inplace=True)
pie_pumpkins.info()
```
အခြားနည်းလမ်းတစ်ခုကတော့ အလွတ်နေသော value များကို column တစ်ခုစီမှ mean value များဖြင့် ဖြည့်ရန် ဖြစ်သည်။
## Simple Linear Regression
[](https://youtu.be/e4c_UP2fSjg "ML for beginners - Linear and Polynomial Regression using Scikit-learn")
> 🎥 Linear Regression နှင့် Polynomial Regression ရဲ့ အကျဉ်းချုပ်ကို ကြည့်ရန် အထက်ပါပုံကို နှိပ်ပါ။
Linear Regression မော်ဒယ်ကို လေ့ကျင့်ရန် **Scikit-learn** library ကို အသုံးပြုပါမည်။
```python
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
```
ပထမဆုံး input values (features) နှင့် ရလဒ် output (label) ကို numpy arrays သို့ ခွဲခြားပါ:
```python
X = pie_pumpkins['DayOfYear'].to_numpy().reshape(-1,1)
y = pie_pumpkins['Price']
```
> Linear Regression package ကို မှန်ကန်စွာ နားလည်စေရန် input data ကို `reshape` ပြုလုပ်ရန် လိုအပ်သည်။ Linear Regression က input အဖြစ် 2D-array ကို မျှော်မှန်းသည်။ အဲဒီ array ရဲ့ row တစ်ခုစီက input features ရဲ့ vector ကို ကိုယ်စားပြုသည်။ ကျွန်ုပ်တို့ရဲ့အခြေအနေမှာ input တစ်ခုသာရှိသောကြောင့် N×1 အရွယ်အစားရှိသော array တစ်ခုလိုအပ်သည်။ N က dataset size ဖြစ်သည်။
ထို့နောက် train dataset နှင့် test dataset များသို့ data ကို ခွဲခြားရန် လိုအပ်သည်။ ဒါက training ပြီးနောက် မော်ဒယ်ကို validate လုပ်နိုင်ရန် ဖြစ်သည်။
```python
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
```
နောက်ဆုံးမှာ Linear Regression မော်ဒယ်ကို training လုပ်ရန် code ၂ လိုင်းသာ လိုအပ်သည်။ `Linear
ကျွန်တော်တို့ရဲ့အမှားဟာ ၂ ခုလောက်မှာရှိပြီး၊ ~17% လောက်ဖြစ်ပါတယ်။ အတော်လေးမကောင်းပါဘူး။ မော်ဒယ်ရဲ့အရည်အသွေးကိုပြသနိုင်တဲ့အခြားအချက်တစ်ခုက **coefficient of determination** ဖြစ်ပြီး၊ ဒီလိုရနိုင်ပါတယ်။
```python
score = lin_reg.score(X_train,y_train)
print('Model determination: ', score)
```
တန်ဖိုးက 0 ဖြစ်ရင်၊ မော်ဒယ်က input data ကိုမထည့်သွင်းစဉ်းစားဘဲ၊ *အဆိုးဆုံး linear predictor* ဖြစ်ပြီး၊ ရလဒ်ရဲ့ပျမ်းမျှတန်ဖိုးကိုသာပြသပါတယ်။ တန်ဖိုးက 1 ဖြစ်ရင်၊ မျှော်မှန်းထားတဲ့ output အားလုံးကိုတိကျစွာခန့်မှန်းနိုင်ပါတယ်။ ကျွန်တော်တို့ရဲ့အခြေအနေမှာ coefficient က 0.06 လောက်ရှိပြီး၊ အတော်လေးနိမ့်ပါတယ်။
ကျွန်တော်တို့ test data ကို regression line နဲ့အတူ plot လုပ်ပြီး၊ regression ကကျွန်တော်တို့အခြေအနေမှာဘယ်လိုအလုပ်လုပ်သလဲဆိုတာပိုမိုမြင်နိုင်ပါတယ်။
```python
plt.scatter(X_test,y_test)
plt.plot(X_test,pred)
```
## Polynomial Regression
Linear Regression ရဲ့အခြားအမျိုးအစားတစ်ခုက Polynomial Regression ဖြစ်ပါတယ်။ တစ်ခါတစ်လေ variable တွေကြား linear relationship ရှိနိုင်ပေမယ့် - ဥပမာ၊ ဖရဲသီးရဲ့အရွယ်အစားကြီးလာတာနဲ့အမျှ၊ စျေးနှုန်းမြင့်လာတာ - တစ်ခါတစ်လေ relationship တွေကို plane သို့မဟုတ်တည့်တည့်လိုင်းအဖြစ် plot လုပ်လို့မရနိုင်ပါဘူး။
✅ [ဒီမှာ](https://online.stat.psu.edu/stat501/lesson/9/9.8) Polynomial Regression အသုံးပြုနိုင်တဲ့ data အမျိုးအစားအချို့ကိုကြည့်ပါ။
Date နဲ့ Price ကြားက relationship ကိုထပ်ကြည့်ပါ။ ဒီ scatterplot ကိုတည့်တည့်လိုင်းနဲ့ခန့်မှန်းသင့်တယ်လို့ထင်ပါသလား။ စျေးနှုန်းတွေကအတက်အကျဖြစ်နိုင်တာမဟုတ်လား။ ဒီအခြေအနေမှာ Polynomial Regression ကိုစမ်းကြည့်နိုင်ပါတယ်။
✅ Polynomial တွေက variable တစ်ခုသို့မဟုတ်အများကြီးနဲ့ coefficient တွေပါဝင်နိုင်တဲ့ mathematical expression တွေဖြစ်ပါတယ်။
Polynomial regression က nonlinear data ကိုပိုမိုတည့်တည့်အောင် curve လိုင်းတစ်ခုဖန်တီးပါတယ်။ ကျွန်တော်တို့အခြေအနေမှာ `DayOfYear` variable ကို input data ထဲမှာ squared အဖြစ်ထည့်သွင်းရင်၊ parabolic curve တစ်ခုနဲ့ data ကို fit လုပ်နိုင်ပြီး၊ curve ရဲ့အနိမ့်ဆုံးအချက်ကိုနှစ်တစ်နှစ်အတွင်းတစ်နေရာမှာရရှိနိုင်ပါမယ်။
Scikit-learn မှာ data processing ရဲ့အဆင့်အမျိုးမျိုးကိုပေါင်းစည်းဖို့အတွက်အသုံးဝင်တဲ့ [pipeline API](https://scikit-learn.org/stable/modules/generated/sklearn.pipeline.make_pipeline.html?highlight=pipeline#sklearn.pipeline.make_pipeline) ပါဝင်ပါတယ်။ **pipeline** က **estimators** တွေရဲ့ chain ဖြစ်ပါတယ်။ ကျွန်တော်တို့အခြေအနေမှာ၊ မော်ဒယ်ကို polynomial features တွေထည့်သွင်းပြီး၊ regression ကို training လုပ်တဲ့ pipeline တစ်ခုဖန်တီးပါမယ်။
```python
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression())
pipeline.fit(X_train,y_train)
```
`PolynomialFeatures(2)` ကိုအသုံးပြုခြင်းက input data ထဲက second-degree polynomials အားလုံးကိုထည့်သွင်းပါမယ်။ ကျွန်တော်တို့အခြေအနေမှာ `DayOfYear`2 ဖြစ်ပြီး၊ input variable X နဲ့ Y နှစ်ခုရှိရင်၊ X2, XY နဲ့ Y2 ကိုထည့်သွင်းပါမယ်။ ပိုမြင့်တဲ့ degree polynomials တွေကိုအသုံးပြုချင်ရင်လည်းရပါတယ်။
Pipelines တွေကို original `LinearRegression` object နဲ့တူညီတဲ့နည်းလမ်းနဲ့အသုံးပြုနိုင်ပြီး၊ pipeline ကို `fit` လုပ်ပြီး၊ `predict` ကိုအသုံးပြုပြီး prediction results ရနိုင်ပါတယ်။ ဒီမှာ test data နဲ့ approximation curve ကိုပြသထားပါတယ်။
Polynomial Regression ကိုအသုံးပြုပြီး MSE နည်းပြီး determination မြင့်တက်နိုင်ပေမယ့်၊ အတော်လေးမထူးခြားပါဘူး။ အခြား feature တွေကိုလည်းထည့်သွင်းစဉ်းစားဖို့လိုအပ်ပါတယ်။
> ဖရဲသီးစျေးနှုန်းအနိမ့်ဆုံးက Halloween အနီးမှာတွေ့ရတာကိုဘယ်လိုရှင်းပြနိုင်မလဲ?
🎃 အားလုံးကိုဂုဏ်ပြုပါတယ်၊ pie ဖရဲသီးရဲ့စျေးနှုန်းကိုခန့်မှန်းနိုင်တဲ့မော်ဒယ်တစ်ခုဖန်တီးနိုင်ခဲ့ပါပြီ။ ဖရဲသီးအမျိုးအစားအားလုံးအတွက်တူညီတဲ့နည်းလမ်းကိုအသုံးပြုနိုင်ပေမယ့်၊ အတော်လေးအလုပ်ရှုပ်ပါတယ်။ အခုတော့ဖရဲသီးအမျိုးအစားကိုမော်ဒယ်ထဲမှာထည့်သွင်းစဉ်းစားနည်းကိုလေ့လာကြပါစို့!
## Categorical Features
အကောင်းဆုံးအခြေအနေမှာ၊ ဖရဲသီးအမျိုးအစားအမျိုးမျိုးအတွက်တူညီတဲ့မော်ဒယ်ကိုအသုံးပြုပြီးစျေးနှုန်းကိုခန့်မှန်းနိုင်ချင်ပါတယ်။ သို့သော် `Variety` column က `Month` ကဲ့သို့ numeric value မပါဝင်ပါဘူး။ ဒီလို column တွေကို **categorical** လို့ခေါ်ပါတယ်။
[](https://youtu.be/DYGliioIAE0 "ML for beginners - Categorical Feature Predictions with Linear Regression")
> 🎥 အထက်ကပုံကိုနှိပ်ပြီး categorical features အသုံးပြုနည်းအကျဉ်းချုပ်ဗီဒီယိုကိုကြည့်ပါ။
ဒီမှာ variety အပေါ်မူတည်ပြီးပျမ်းမျှစျေးနှုန်းကိုမြင်နိုင်ပါတယ်။
Variety ကိုစဉ်းစားဖို့အတွက်၊ variety ကို numeric form သို့မဟုတ် **encode** လုပ်ဖို့လိုအပ်ပါတယ်။ encode လုပ်နည်းအမျိုးမျိုးရှိပါတယ်-
* **Numeric encoding** က variety အမျိုးအစားတွေကို table တစ်ခုထဲမှာတည်ဆောက်ပြီး၊ variety နာမည်ကို table ထဲက index နဲ့အစားထိုးပါမယ်။ ဒါဟာ linear regression အတွက်အကောင်းဆုံးနည်းလမ်းမဟုတ်ပါဘူး၊ အကြောင်းက linear regression က index ရဲ့ actual numeric value ကိုယူပြီး၊ coefficient တစ်ခုနဲ့မြှောက်ပြီးရလဒ်ထဲထည့်သွင်းပါတယ်။ ကျွန်တော်တို့အခြေအနေမှာ index နံပါတ်နဲ့စျေးနှုန်းကြားက relationship က non-linear ဖြစ်ပါတယ်၊ indices တွေကိုအတိအကျစီစဉ်ထားတယ်ဆိုရင်တောင်ပါ။
* **One-hot encoding** က `Variety` column ကို variety တစ်ခုစီအတွက် column ၄ ခုနဲ့အစားထိုးပါမယ်။ တစ်ခုချင်းစီ column မှာ၊ row တစ်ခုဟာအတိအကျ variety တစ်ခုဖြစ်ရင် `1` ပါမယ်၊ မဟုတ်ရင် `0` ပါမယ်။ ဒါက linear regression မှာ variety တစ်ခုချင်းစီအတွက် coefficient ၄ ခုပါဝင်ပြီး၊ အဲဒီ variety အတွက် "starting price" (သို့မဟုတ် "additional price") ကိုတာဝန်ယူပါမယ်။
Variety ကို one-hot encode လုပ်နည်းကိုအောက်မှာပြထားပါတယ်-
```python
pd.get_dummies(new_pumpkins['Variety'])
```
ID | FAIRYTALE | MINIATURE | MIXED HEIRLOOM VARIETIES | PIE TYPE
----|-----------|-----------|--------------------------|----------
70 | 0 | 0 | 0 | 1
71 | 0 | 0 | 0 | 1
... | ... | ... | ... | ...
1738 | 0 | 1 | 0 | 0
1739 | 0 | 1 | 0 | 0
1740 | 0 | 1 | 0 | 0
1741 | 0 | 1 | 0 | 0
1742 | 0 | 1 | 0 | 0
One-hot encoded variety ကို input အဖြစ်အသုံးပြုပြီး linear regression ကို training လုပ်ဖို့အတွက်၊ `X` နဲ့ `y` data ကိုမှန်ကန်စွာ initialize လုပ်ဖို့လိုအပ်ပါတယ်-
```python
X = pd.get_dummies(new_pumpkins['Variety'])
y = new_pumpkins['Price']
```
အပေါ်မှာ Linear Regression ကို training လုပ်ဖို့အသုံးပြုတဲ့ code နဲ့အတူတူပါပဲ။ စမ်းကြည့်ရင်၊ mean squared error ကအတော်လေးတူတူပါပေမယ့်၊ coefficient of determination (~77%) ကပိုမြင့်တက်ပါတယ်။ ပိုမိုတိကျတဲ့ခန့်မှန်းချက်ရဖို့အတွက်၊ categorical features တွေ၊ နဲ့ numeric features တွေဖြစ်တဲ့ `Month` သို့မဟုတ် `DayOfYear` ကိုထည့်သွင်းစဉ်းစားနိုင်ပါတယ်။ feature တွေကိုတစ်စုတစ်စည်းအဖြစ်ရဖို့ `join` ကိုအသုံးပြုနိုင်ပါတယ်-
```python
X = pd.get_dummies(new_pumpkins['Variety']) \
.join(new_pumpkins['Month']) \
.join(pd.get_dummies(new_pumpkins['City'])) \
.join(pd.get_dummies(new_pumpkins['Package']))
y = new_pumpkins['Price']
```
ဒီမှာ `City` နဲ့ `Package` type ကိုလည်းထည့်သွင်းထားပြီး၊ MSE 2.84 (10%) နဲ့ determination 0.94 ရရှိပါတယ်!
## Putting it all together
အကောင်းဆုံးမော်ဒယ်ကိုဖန်တီးဖို့အတွက်၊ အပေါ်ကဥပမာထဲက combined (one-hot encoded categorical + numeric) data ကို Polynomial Regression နဲ့အတူအသုံးပြုနိုင်ပါတယ်။ အောက်မှာအပြည့်အစုံ code ကိုပြထားပါတယ်-
```python
# set up training data
X = pd.get_dummies(new_pumpkins['Variety']) \
.join(new_pumpkins['Month']) \
.join(pd.get_dummies(new_pumpkins['City'])) \
.join(pd.get_dummies(new_pumpkins['Package']))
y = new_pumpkins['Price']
# make train-test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# setup and train the pipeline
pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression())
pipeline.fit(X_train,y_train)
# predict results for test data
pred = pipeline.predict(X_test)
# calculate MSE and determination
mse = np.sqrt(mean_squared_error(y_test,pred))
print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)')
score = pipeline.score(X_train,y_train)
print('Model determination: ', score)
```
ဒီနည်းလမ်းက determination coefficient 97% နီးပါးနဲ့ MSE=2.23 (~8% prediction error) ရရှိစေပါမယ်။
| Model | MSE | Determination |
|-------|-----|---------------|
| `DayOfYear` Linear | 2.77 (17.2%) | 0.07 |
| `DayOfYear` Polynomial | 2.73 (17.0%) | 0.08 |
| `Variety` Linear | 5.24 (19.7%) | 0.77 |
| All features Linear | 2.84 (10.5%) | 0.94 |
| All features Polynomial | 2.23 (8.25%) | 0.97 |
🏆 အားလုံးကိုဂုဏ်ပြုပါတယ်! Regression models ၄ ခုကိုတစ်ခန်းတည်းမှာဖန်တီးပြီး၊ မော်ဒယ်ရဲ့အရည်အသွေးကို 97% အထိတိုးတက်စေခဲ့ပါတယ်။ Regression ရဲ့နောက်ဆုံးအပိုင်းမှာ၊ category တွေကိုသတ်မှတ်ဖို့ Logistic Regression ကိုလေ့လာပါမယ်။
---
## 🚀Challenge
ဒီ notebook ထဲမှာ variable အမျိုးမျိုးကိုစမ်းကြည့်ပြီး၊ correlation နဲ့ model accuracy ကြားကဆက်နွယ်မှုကိုကြည့်ပါ။
## [Post-lecture quiz](https://ff-quizzes.netlify.app/en/ml/)
## Review & Self Study
ဒီခန်းမှာ Linear Regression ကိုလေ့လာခဲ့ပါတယ်။ Regression ရဲ့အရေးကြီးတဲ့အမျိုးအစားအခြားများလည်းရှိပါတယ်။ Stepwise, Ridge, Lasso နဲ့ Elasticnet techniques တွေကိုဖတ်ရှုပါ။ ပိုမိုလေ့လာချင်ရင် [Stanford Statistical Learning course](https://online.stanford.edu/courses/sohs-ystatslearning-statistical-learning) ကိုလေ့လာပါ။
## Assignment
[Build a Model](assignment.md)
---
**ဝက်ဘ်ဆိုက်မှတ်ချက်**:
ဤစာရွက်စာတမ်းကို AI ဘာသာပြန်ဝန်ဆောင်မှု [Co-op Translator](https://github.com/Azure/co-op-translator) ကို အသုံးပြု၍ ဘာသာပြန်ထားပါသည်။ ကျွန်ုပ်တို့သည် တိကျမှန်ကန်မှုအတွက် ကြိုးစားနေပါသော်လည်း၊ အလိုအလျောက်ဘာသာပြန်ဆိုမှုများတွင် အမှားများ သို့မဟုတ် မတိကျမှုများ ပါဝင်နိုင်သည်ကို ကျေးဇူးပြု၍ သတိပြုပါ။ မူရင်းဘာသာစကားဖြင့် ရေးသားထားသော စာရွက်စာတမ်းကို အာဏာတည်သော ရင်းမြစ်အဖြစ် သတ်မှတ်သင့်ပါသည်။ အရေးကြီးသော အချက်အလက်များအတွက် လူက ဘာသာပြန်ဝန်ဆောင်မှုကို အသုံးပြုရန် အကြံပြုပါသည်။ ဤဘာသာပြန်ကို အသုံးပြုခြင်းမှ ဖြစ်ပေါ်လာသော နားလည်မှုမှားများ သို့မဟုတ် အဓိပ္ပာယ်မှားများအတွက် ကျွန်ုပ်တို့သည် တာဝန်မယူပါ။