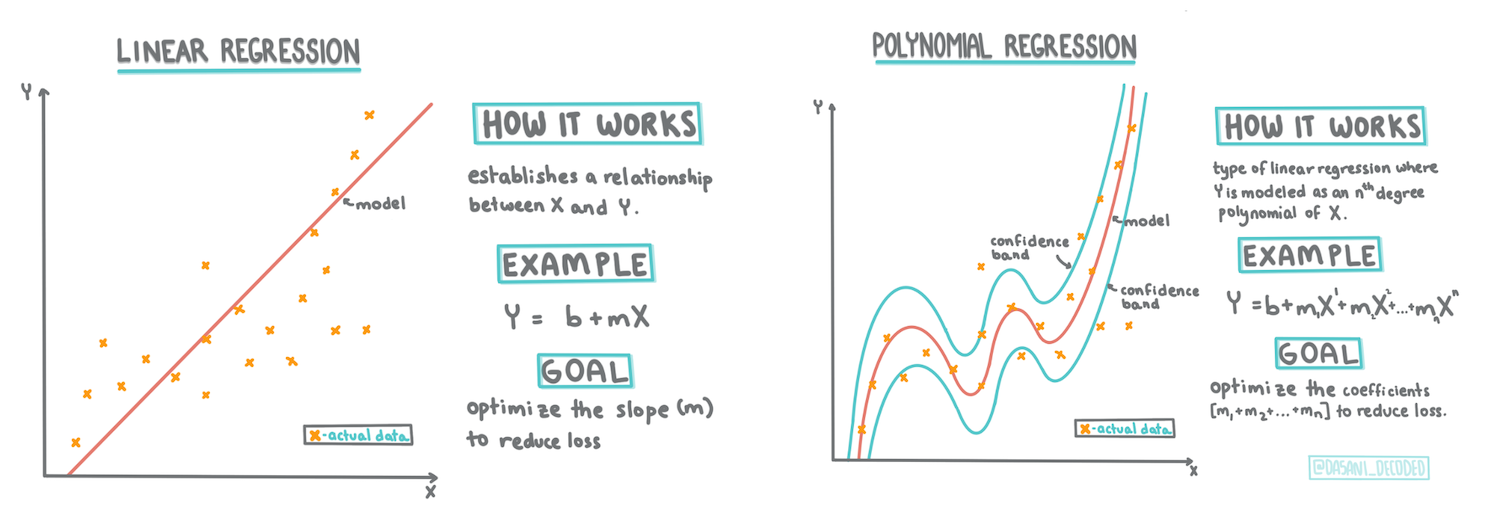
# Scikit-learn वापरून रिग्रेशन मॉडेल तयार करा: चार प्रकारे रिग्रेशन  > माहितीग्राफिक [दसानी मदीपल्ली](https://twitter.com/dasani_decoded) यांच्याकडून ## [पूर्व-व्याख्यान क्विझ](https://ff-quizzes.netlify.app/en/ml/) > ### [हा धडा R मध्ये उपलब्ध आहे!](../../../../2-Regression/3-Linear/solution/R/lesson_3.html) ### परिचय आतापर्यंत तुम्ही कद्दूच्या किंमतींच्या डेटासेटवर आधारित नमुना डेटासह रिग्रेशन म्हणजे काय हे शोधले आहे, जे आपण या धड्यादरम्यान वापरणार आहोत. तुम्ही ते Matplotlib वापरून व्हिज्युअलाइझ देखील केले आहे. आता तुम्ही मशीन लर्निंगसाठी रिग्रेशनमध्ये अधिक खोलवर जाण्यास तयार आहात. व्हिज्युअलायझेशन डेटाचा अर्थ लावण्यास मदत करते, परंतु मशीन लर्निंगची खरी ताकद _मॉडेल प्रशिक्षण_ यामध्ये आहे. मॉडेल ऐतिहासिक डेटावर प्रशिक्षण दिले जाते जेणेकरून डेटाच्या परस्परसंबंधांना स्वयंचलितपणे कॅप्चर करता येईल आणि नवीन डेटासाठी परिणामांची भविष्यवाणी करता येईल, जे मॉडेलने यापूर्वी पाहिलेले नाही. या धड्यात, तुम्ही रिग्रेशनचे दोन प्रकार शिकाल: _मूलभूत रेखीय रिग्रेशन_ आणि _बहुपद रिग्रेशन_, तसेच या तंत्रांच्या पाठीमागील काही गणित. ही मॉडेल्स आपल्याला विविध इनपुट डेटावर आधारित कद्दूच्या किंमतींची भविष्यवाणी करण्यास अनुमती देतील. [](https://youtu.be/CRxFT8oTDMg "मशीन लर्निंगसाठी नवशिक्यांसाठी - रेखीय रिग्रेशन समजून घेणे") > 🎥 वरील प्रतिमेवर क्लिक करा रेखीय रिग्रेशनचा संक्षिप्त व्हिडिओ आढावा पाहण्यासाठी. > या अभ्यासक्रमात, आम्ही गणिताचे किमान ज्ञान गृहीत धरतो आणि इतर क्षेत्रांमधून येणाऱ्या विद्यार्थ्यांसाठी ते सुलभ करण्याचा प्रयत्न करतो. त्यामुळे नोट्स, 🧮 गणना, आकृत्या आणि समज वाढवण्यासाठी इतर शिकण्याची साधने शोधा. ### पूर्वअट आतापर्यंत तुम्ही कद्दूच्या डेटाच्या रचनेशी परिचित असले पाहिजे, ज्याचा आपण अभ्यास करत आहोत. हे डेटासेट या धड्याच्या _notebook.ipynb_ फाईलमध्ये पूर्व-लोड केलेले आणि पूर्व-स्वच्छ केलेले आहे. फाईलमध्ये, कद्दूची किंमत नवीन डेटा फ्रेममध्ये प्रति बशेल दर्शविली जाते. Visual Studio Code मध्ये नोटबुक चालवू शकता याची खात्री करा. ### तयारी तुम्ही हे डेटा लोड करत आहात याची आठवण करून द्या जेणेकरून त्यावर प्रश्न विचारता येतील. - कधी कद्दू खरेदी करणे सर्वात चांगले आहे? - मिनिएचर कद्दूंच्या एका केसची किंमत किती अपेक्षित आहे? - मला ते अर्ध्या बशेलच्या टोपलीत खरेदी करावे का किंवा 1 1/9 बशेल बॉक्समध्ये? चला या डेटामध्ये अधिक खोदून पाहूया. मागील धड्यात, तुम्ही Pandas डेटा फ्रेम तयार केली आणि ती मूळ डेटासेटच्या भागाने भरली, किंमती बशेलने प्रमाणित केल्या. असे करून, तुम्हाला सुमारे 400 डेटा पॉइंट्स आणि फक्त शरद ऋतूतील महिन्यांसाठी डेटा गोळा करता आला. या धड्याच्या सोबतच्या नोटबुकमध्ये पूर्व-लोड केलेल्या डेटावर एक नजर टाका. डेटा पूर्व-लोड केलेला आहे आणि महिन्याच्या डेटाचे प्रारंभिक स्कॅटरप्लॉट तयार केले आहे. कदाचित आपण डेटा अधिक स्वच्छ करून त्याच्या स्वरूपाबद्दल अधिक तपशील मिळवू शकतो. ## रेखीय रिग्रेशन रेषा धडा 1 मध्ये तुम्ही शिकलात की, रेखीय रिग्रेशनचा उद्देश म्हणजे एक रेषा प्लॉट करणे: - **चलांचे परस्परसंबंध दाखवा**. चलांमधील परस्परसंबंध दाखवा - **भविष्यवाणी करा**. नवीन डेटा पॉइंट त्या रेषेच्या संदर्भात कुठे असेल याची अचूक भविष्यवाणी करा. **लीस्ट-स्क्वेअर्स रिग्रेशन** सहसा या प्रकारची रेषा काढण्यासाठी वापरली जाते. 'लीस्ट-स्क्वेअर्स' या संज्ञेचा अर्थ असा आहे की रिग्रेशन रेषेभोवती असलेल्या सर्व डेटा पॉइंट्सचे वर्ग केले जातात आणि नंतर त्यांची बेरीज केली जाते. आदर्शतः, ती अंतिम बेरीज शक्य तितकी लहान असावी, कारण आपल्याला कमी चुका हव्या आहेत, किंवा `लीस्ट-स्क्वेअर्स`. हे असे करतो कारण आम्हाला अशी रेषा मॉडेल करायची आहे ज्यामध्ये आपल्या सर्व डेटा पॉइंट्सपासून किमान एकत्रित अंतर आहे. तसेच, आम्ही अटींचा वर्ग करतो कारण आम्हाला त्याच्या दिशेऐवजी त्याच्या परिमाणाची काळजी आहे. 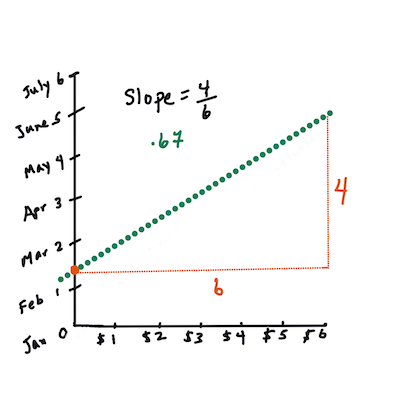> **🧮 गणित दाखवा** > > ही रेषा, ज्याला _सर्वोत्तम तंदुरुस्तीची रेषा_ म्हणतात, [एका समीकरणाने](https://en.wikipedia.org/wiki/Simple_linear_regression) व्यक्त केली जाऊ शकते: > > ``` > Y = a + bX > ``` > > `X` हा 'स्पष्टीकरणात्मक चल' आहे. `Y` हा 'अवलंबित चल' आहे. रेषेचा उतार `b` आहे आणि `a` हा वाय-अवरोध आहे, जो `X = 0` असताना `Y` च्या मूल्याचा संदर्भ घेतो. > >  > > प्रथम, उतार `b` काढा. माहितीग्राफिक [जेन लूपर](https://twitter.com/jenlooper) यांच्याकडून. > > दुसऱ्या शब्दांत, आणि आपल्या कद्दू डेटाच्या मूळ प्रश्नाचा संदर्भ घेत: "महिन्यानुसार प्रति बशेल कद्दूची किंमत भाकीत करा", `X` किंमतीचा संदर्भ घेईल आणि `Y` विक्रीच्या महिन्याचा संदर्भ घेईल. 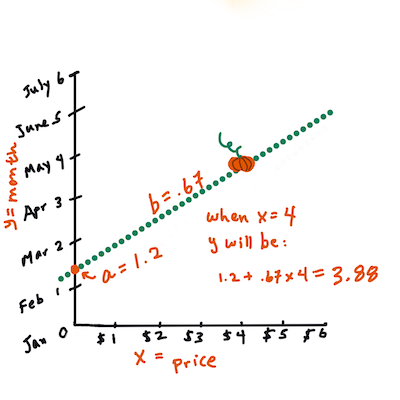> >  > > `Y` चे मूल्य काढा. जर तुम्ही सुमारे $4 देत असाल, तर तो एप्रिल असणार! माहितीग्राफिक [जेन लूपर](https://twitter.com/jenlooper) यांच्याकडून. > > रेषेचा उतार काढण्यासाठी गणित अवरोधावर अवलंबून असते, किंवा `X = 0` असताना `Y` कुठे आहे. > > या मूल्यांच्या गणनेची पद्धत [Math is Fun](https://www.mathsisfun.com/data/least-squares-regression.html) वेबसाइटवर पाहू शकता. तसेच [हा लीस्ट-स्क्वेअर्स कॅल्क्युलेटर](https://www.mathsisfun.com/data/least-squares-calculator.html) भेट द्या आणि कसे आकडे रेषेवर परिणाम करतात ते पाहा. ## सहसंबंध समजून घेण्यासारखी आणखी एक संज्ञा म्हणजे दिलेल्या X आणि Y चलांमधील **सहसंबंध गुणांक**. स्कॅटरप्लॉट वापरून तुम्ही हा गुणांक पटकन व्हिज्युअलाइझ करू शकता. जर प्लॉटमधील डेटा पॉइंट्स एका नीट रेषेत विखुरलेले असतील तर त्यात उच्च सहसंबंध असतो, परंतु जर डेटा पॉइंट्स X आणि Y दरम्यान सर्वत्र विखुरलेले असतील तर त्यात कमी सहसंबंध असतो. एक चांगले रेखीय रिग्रेशन मॉडेल असेल ज्यामध्ये लीस्ट-स्क्वेअर्स रिग्रेशन पद्धतीसह रिग्रेशन रेषेचा वापर करून उच्च (1 च्या जवळ) सहसंबंध गुणांक असेल. ✅ या धड्याच्या सोबतच्या नोटबुकमध्ये स्कॅटरप्लॉट चालवा आणि महिना ते किंमत डेटा पाहा. कद्दू विक्रीसाठी महिना ते किंमत डेटा उच्च किंवा कमी सहसंबंध दर्शवतो का? जर तुम्ही `महिना` ऐवजी अधिक सूक्ष्म मोजमाप वापरले (उदा. *वर्षाचा दिवस* म्हणजेच वर्षाच्या सुरुवातीपासूनचे दिवस) तर ते बदलते का? वरील कोडमध्ये, आम्ही गृहीत धरतो की आम्ही डेटा स्वच्छ केला आहे आणि `new_pumpkins` नावाचा डेटा फ्रेम प्राप्त केला आहे, जो खालीलप्रमाणे आहे: ID | महिना | वर्षाचा दिवस | प्रकार | शहर | पॅकेज | कमी किंमत | जास्त किंमत | किंमत ---|-------|-----------|---------|------|---------|-----------|------------|------- 70 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 15.0 | 15.0 | 13.636364 71 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 18.0 | 18.0 | 16.363636 72 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 18.0 | 18.0 | 16.363636 73 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 17.0 | 17.0 | 15.454545 74 | 10 | 281 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 15.0 | 15.0 | 13.636364 > डेटा स्वच्छ करण्यासाठी कोड [`notebook.ipynb`](../../../../2-Regression/3-Linear/notebook.ipynb) मध्ये उपलब्ध आहे. आम्ही मागील धडातील समान स्वच्छता पावले घेतली आहेत आणि खालील अभिव्यक्ती वापरून `DayOfYear` स्तंभाची गणना केली आहे: ```python day_of_year = pd.to_datetime(pumpkins['Date']).apply(lambda dt: (dt-datetime(dt.year,1,1)).days) ``` आता तुम्हाला रेखीय रिग्रेशनमागील गणित समजले आहे, चला रिग्रेशन मॉडेल तयार करूया आणि पाहूया की कद्दूच्या पॅकेजसाठी सर्वोत्तम किंमतींची भविष्यवाणी करता येते का. एखाद्या सुट्टीतील कद्दूच्या पॅचसाठी कद्दू खरेदी करणाऱ्या व्यक्तीला कदाचित कद्दूच्या पॅकेजेसची खरेदी ऑप्टिमाइझ करण्यासाठी ही माहिती हवी असेल. ## सहसंबंध शोधणे [](https://youtu.be/uoRq-lW2eQo "मशीन लर्निंगसाठी नवशिक्यांसाठी - सहसंबंध शोधणे: रेखीय रिग्रेशनची गुरुकिल्ली") > 🎥 वरील प्रतिमेवर क्लिक करा सहसंबंधाचा संक्षिप्त व्हिडिओ आढावा पाहण्यासाठी. मागील धडामध्ये तुम्ही कदाचित पाहिले असेल की विविध महिन्यांसाठी सरासरी किंमत अशी दिसते: हे सूचित करते की काही सहसंबंध असावा, आणि आपण `महिना` आणि `किंमत` यांच्यातील किंवा `वर्षाचा दिवस` आणि `किंमत` यांच्यातील संबंध भाकीत करण्यासाठी रेखीय रिग्रेशन मॉडेल प्रशिक्षण देण्याचा प्रयत्न करू शकतो. खालील स्कॅटरप्लॉट नातेसंबंध दर्शवतो: चला `corr` फंक्शन वापरून सहसंबंध तपासूया: ```python print(new_pumpkins['Month'].corr(new_pumpkins['Price'])) print(new_pumpkins['DayOfYear'].corr(new_pumpkins['Price'])) ``` असे दिसते की सहसंबंध खूपच कमी आहे, `महिना` साठी -0.15 आणि `वर्षाचा दिवस` साठी -0.17, परंतु आणखी एक महत्त्वाचा संबंध असू शकतो. असे दिसते की विविध कद्दू प्रकारांशी संबंधित किंमतींचे वेगवेगळे क्लस्टर आहेत. ही गृहीतके पुष्टी करण्यासाठी, चला प्रत्येक कद्दू प्रकार वेगळ्या रंगात प्लॉट करूया. `scatter` प्लॉटिंग फंक्शनला `ax` पॅरामीटर पास करून आपण सर्व पॉइंट्स एकाच ग्राफवर प्लॉट करू शकतो: ```python ax=None colors = ['red','blue','green','yellow'] for i,var in enumerate(new_pumpkins['Variety'].unique()): df = new_pumpkins[new_pumpkins['Variety']==var] ax = df.plot.scatter('DayOfYear','Price',ax=ax,c=colors[i],label=var) ``` आपल्या तपासणीने सूचित केले की प्रकाराचा एकूण किंमतीवर विक्रीच्या तारखेपेक्षा जास्त परिणाम होतो. आपण हे बार ग्राफसह पाहू शकतो: ```python new_pumpkins.groupby('Variety')['Price'].mean().plot(kind='bar') ``` आता आपण फक्त एका कद्दू प्रकारावर लक्ष केंद्रित करूया, 'पाई प्रकार', आणि पाहूया की तारखेचा किंमतीवर काय परिणाम होतो: ```python pie_pumpkins = new_pumpkins[new_pumpkins['Variety']=='PIE TYPE'] pie_pumpkins.plot.scatter('DayOfYear','Price') ``` जर आपण आता `corr` फंक्शन वापरून `किंमत` आणि `वर्षाचा दिवस` यांच्यातील सहसंबंधाची गणना केली, तर आपल्याला सुमारे `-0.27` मिळेल - याचा अर्थ असा की भाकीत मॉडेल प्रशिक्षण देणे योग्य आहे. > रेखीय रिग्रेशन मॉडेल प्रशिक्षण देण्यापूर्वी, आपला डेटा स्वच्छ असल्याची खात्री करणे महत्त्वाचे आहे. रेखीय रिग्रेशन रिक्त मूल्यांसह चांगले कार्य करत नाही, त्यामुळे सर्व रिक्त पेशी काढून टाकणे योग्य ठरेल: ```python pie_pumpkins.dropna(inplace=True) pie_pumpkins.info() ``` आणखी एक दृष्टिकोन म्हणजे त्या रिक्त मूल्यांना संबंधित स्तंभातील सरासरी मूल्यांनी भरून काढणे. ## साधे रेखीय रिग्रेशन [](https://youtu.be/e4c_UP2fSjg "मशीन लर्निंगसाठी नवशिक्यांसाठी - Scikit-learn वापरून रेखीय आणि बहुपद रिग्रेशन") > 🎥 वरील प्रतिमेवर क्लिक करा रेखीय आणि बहुपद रिग्रेशनचा संक्षिप्त व्हिडिओ आढावा पाहण्यासाठी. आमच्या रेखीय रिग्रेशन मॉडेलला प्रशिक्षण देण्यासाठी, आम्ही **Scikit-learn** लायब्ररी वापरणार आहोत. ```python from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error from sklearn.model_selection import train_test_split ``` आम्ही इनपुट मूल्ये (वैशिष्ट्ये) आणि अपेक्षित आउटपुट (लेबल) वेगळ्या numpy ऍरेमध्ये विभाजित करून सुरुवात करतो: ```python X = pie_pumpkins['DayOfYear'].to_numpy().reshape(-1,1) y = pie_pumpkins['Price'] ``` > लक्षात घ्या की रेखीय रिग्रेशन पॅकेजने ते योग्यरित्या समजण्यासाठी आम्हाला इनपुट डेटावर `reshape` करावे लागले. रेखीय रिग्रेशनला 2D-ऍरे इनपुट म्हणून अपेक्षित आहे, जिथे ऍरेमधील प्रत्येक पंक्ती इनपुट वैशिष्ट्यांच्या व्हेक्टरशी संबंधित आहे. आपल्या प्रकरणात, कारण आपल्याकडे फक्त एक इनपुट आहे - आपल्याला N×1 आकाराचे ऍरे आवश्यक आहे, जिथे N डेटासेटचा आकार आहे. यानंतर, आम्हाला डेटा ट्रेन आणि टेस्ट डेटासेटमध्ये विभाजित करणे आवश्यक आहे, जेणेकरून प्रशिक्षणानंतर आम्ही आमच्या मॉडेलची पडताळणी करू शकू: ```python X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) ``` शेवटी, वास्तविक रेखीय रिग्रेशन मॉडेल प्रशिक्षण देणे फक्त दोन ओळींचे काम आहे. आम्ही `LinearRegression` ऑब्जेक्ट परिभाषित करतो आणि `fit` पद्धतीचा वापर करून आमच्या डेटावर फिट करतो: ```python lin_reg = LinearRegression() lin_reg.fit(X_train,y_train) ``` `LinearRegression` ऑब्जेक्टमध्ये `fit` केल्यानंतर सर्व रिग्रेशन गुणांक असतात, जे `.coef_` प्रॉपर्टी वापरून प्रवेश करता येतात. आपल्या प्रकरणात, फक्त एक गुणांक आहे, जो सुमारे `-0.017` असावा. याचा अर्थ किंमती कालांतराने किंचित कमी होत आहेत, परंतु फार नाही, दररोज सुमारे 2 सेंट. आम्ही `lin_reg.inter आमची चूक सुमारे 2 मुद्द्यांवर आहे, जी ~17% आहे. फारशी चांगली नाही. मॉडेल गुणवत्तेचा आणखी एक निर्देशक म्हणजे **निर्धारण गुणांक**, जो खालीलप्रमाणे मिळवता येतो: ```python score = lin_reg.score(X_train,y_train) print('Model determination: ', score) ``` जर मूल्य 0 असेल, तर याचा अर्थ मॉडेल इनपुट डेटा विचारात घेत नाही आणि *सर्वात वाईट रेषीय भविष्यवक्ता* म्हणून कार्य करते, जो फक्त निकालाचा सरासरी मूल्य आहे. मूल्य 1 असल्यास, आपण सर्व अपेक्षित आउटपुट पूर्णपणे अंदाज करू शकतो. आमच्या बाबतीत, निर्धारण गुणांक सुमारे 0.06 आहे, जो खूपच कमी आहे. आम्ही चाचणी डेटा आणि रेषीय रिग्रेशन लाइन एकत्र प्लॉट करू शकतो, ज्यामुळे आमच्या बाबतीत रिग्रेशन कसे कार्य करते हे चांगल्या प्रकारे दिसेल: ```python plt.scatter(X_test,y_test) plt.plot(X_test,pred) ``` ## बहुपद रिग्रेशन रेषीय रिग्रेशनचा आणखी एक प्रकार म्हणजे बहुपद रिग्रेशन. कधी कधी व्हेरिएबल्समध्ये रेषीय संबंध असतो - जसे की भोपळ्याचा आकार मोठा असेल तर किंमत जास्त असेल - परंतु कधी कधी हे संबंध सरळ रेषा किंवा पृष्ठभाग म्हणून प्लॉट करता येत नाहीत. ✅ येथे [काही अधिक उदाहरणे](https://online.stat.psu.edu/stat501/lesson/9/9.8) आहेत ज्यामध्ये बहुपद रिग्रेशनचा उपयोग होऊ शकतो. Date आणि Price यांच्यातील संबंध पुन्हा एकदा पाहा. हा स्कॅटरप्लॉट सरळ रेषेने विश्लेषित केला जावा असे वाटते का? किंमती बदलू शकत नाहीत का? अशा परिस्थितीत, तुम्ही बहुपद रिग्रेशन वापरून पाहू शकता. ✅ बहुपद म्हणजे गणितीय अभिव्यक्ती ज्यामध्ये एक किंवा अधिक व्हेरिएबल्स आणि गुणांक असू शकतात. बहुपद रिग्रेशन वाकवलेली रेषा तयार करते जी नॉन-रेषीय डेटाशी चांगल्या प्रकारे जुळते. आमच्या बाबतीत, जर आम्ही `DayOfYear` व्हेरिएबलचे वर्ग समाविष्ट केले, तर आम्ही आमचा डेटा एका परबोलिक वक्राने फिट करू शकतो, ज्याचा किमान बिंदू वर्षाच्या विशिष्ट बिंदूवर असेल. Scikit-learn मध्ये डेटा प्रोसेसिंगच्या विविध टप्प्यांना एकत्र करण्यासाठी एक उपयुक्त [pipeline API](https://scikit-learn.org/stable/modules/generated/sklearn.pipeline.make_pipeline.html?highlight=pipeline#sklearn.pipeline.make_pipeline) समाविष्ट आहे. **पाइपलाइन** म्हणजे **अंदाजकांची** साखळी. आमच्या बाबतीत, आम्ही एक पाइपलाइन तयार करू जी प्रथम मॉडेलमध्ये बहुपद वैशिष्ट्ये जोडते आणि नंतर रिग्रेशन प्रशिक्षित करते: ```python from sklearn.preprocessing import PolynomialFeatures from sklearn.pipeline import make_pipeline pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression()) pipeline.fit(X_train,y_train) ``` `PolynomialFeatures(2)` वापरण्याचा अर्थ असा आहे की आम्ही इनपुट डेटामधून सर्व दुसऱ्या-डिग्री बहुपद समाविष्ट करू. आमच्या बाबतीत याचा अर्थ फक्त `DayOfYear`<sup>2</sup> असेल, परंतु दोन इनपुट व्हेरिएबल्स X आणि Y दिल्यास, हे X<sup>2</sup>, XY आणि Y<sup>2</sup> जोडेल. आम्ही हवे असल्यास उच्च डिग्री बहुपद देखील वापरू शकतो. पाइपलाइन मूळ `LinearRegression` ऑब्जेक्टप्रमाणेच वापरली जाऊ शकते, म्हणजेच आम्ही पाइपलाइन `fit` करू शकतो आणि नंतर `predict` वापरून अंदाज परिणाम मिळवू शकतो. येथे चाचणी डेटा आणि अंदाज वक्र दर्शविणारा ग्राफ आहे: बहुपद रिग्रेशन वापरून, आम्हाला किंचित कमी MSE आणि उच्च निर्धारण मिळू शकते, परंतु फारसे महत्त्वाचे नाही. आम्हाला इतर वैशिष्ट्यांचा विचार करणे आवश्यक आहे! > तुम्ही पाहू शकता की किमान भोपळ्याच्या किंमती हॅलोविनच्या आसपास दिसतात. तुम्ही हे कसे स्पष्ट कराल? 🎃 अभिनंदन, तुम्ही एक मॉडेल तयार केले आहे जे पाई भोपळ्याच्या किंमतींचा अंदाज लावण्यास मदत करू शकते. तुम्ही कदाचित सर्व प्रकारच्या भोपळ्यांसाठी हीच प्रक्रिया पुन्हा करू शकता, परंतु ते कंटाळवाणे होईल. आता आपण आपल्या मॉडेलमध्ये भोपळ्याच्या प्रकाराचा विचार कसा करायचा ते शिकूया! ## श्रेणी वैशिष्ट्ये आदर्श जगात, आम्हाला एकाच मॉडेलचा वापर करून भोपळ्याच्या विविध प्रकारांसाठी किंमतींचा अंदाज लावता यावा अशी इच्छा आहे. तथापि, `Variety` कॉलम `Month` सारख्या कॉलमपेक्षा थोडा वेगळा आहे, कारण त्यामध्ये नॉन-न्यूमेरिक मूल्ये आहेत. अशा कॉलम्सला **श्रेणी** म्हणतात. [](https://youtu.be/DYGliioIAE0 "ML for beginners - श्रेणी वैशिष्ट्यांसह रेषीय रिग्रेशन") > 🎥 वरील प्रतिमेवर क्लिक करा श्रेणी वैशिष्ट्यांचा वापर करण्याचा संक्षिप्त व्हिडिओ पाहण्यासाठी. येथे तुम्ही पाहू शकता की प्रकारानुसार सरासरी किंमत कशी बदलते: प्रकाराचा विचार करण्यासाठी, प्रथम त्याला न्यूमेरिक स्वरूपात रूपांतरित करणे आवश्यक आहे, किंवा **एन्कोड** करणे आवश्यक आहे. हे करण्याचे अनेक मार्ग आहेत: * साधे **न्यूमेरिक एन्कोडिंग** विविध प्रकारांची एक टेबल तयार करेल आणि नंतर प्रकाराचे नाव त्या टेबलमधील निर्देशांकाने बदलले जाईल. हे रेषीय रिग्रेशनसाठी सर्वोत्तम कल्पना नाही, कारण रेषीय रिग्रेशन निर्देशांकाच्या वास्तविक न्यूमेरिक मूल्याचा विचार करते आणि काही गुणांकाने गुणाकार करून निकालात जोडते. आमच्या बाबतीत, निर्देशांक क्रमांक आणि किंमत यांच्यातील संबंध स्पष्टपणे नॉन-रेषीय आहे, जरी आम्ही सुनिश्चित केले की निर्देशांक विशिष्ट क्रमाने आहेत. * **वन-हॉट एन्कोडिंग** `Variety` कॉलम 4 वेगळ्या कॉलम्सने बदलेल, प्रत्येक प्रकारासाठी एक. प्रत्येक कॉलममध्ये `1` असेल जर संबंधित रांग दिलेल्या प्रकाराची असेल, आणि `0` अन्यथा. याचा अर्थ असा की रेषीय रिग्रेशनमध्ये चार गुणांक असतील, प्रत्येक भोपळ्याच्या प्रकारासाठी एक, त्या विशिष्ट प्रकारासाठी "प्रारंभिक किंमत" (किंवा "अतिरिक्त किंमत") जबाबदार. खालील कोड प्रकार वन-हॉट एन्कोड कसा करता येतो हे दाखवतो: ```python pd.get_dummies(new_pumpkins['Variety']) ``` ID | FAIRYTALE | MINIATURE | MIXED HEIRLOOM VARIETIES | PIE TYPE ----|-----------|-----------|--------------------------|---------- 70 | 0 | 0 | 0 | 1 71 | 0 | 0 | 0 | 1 ... | ... | ... | ... | ... 1738 | 0 | 1 | 0 | 0 1739 | 0 | 1 | 0 | 0 1740 | 0 | 1 | 0 | 0 1741 | 0 | 1 | 0 | 0 1742 | 0 | 1 | 0 | 0 वन-हॉट एन्कोड केलेला प्रकार इनपुट म्हणून वापरून रेषीय रिग्रेशन प्रशिक्षित करण्यासाठी, आम्हाला फक्त `X` आणि `y` डेटा योग्य प्रकारे प्रारंभ करणे आवश्यक आहे: ```python X = pd.get_dummies(new_pumpkins['Variety']) y = new_pumpkins['Price'] ``` उर्वरित कोड वर वापरलेल्या रेषीय रिग्रेशन प्रशिक्षित करण्यासाठी समान आहे. जर तुम्ही प्रयत्न केला, तर तुम्हाला दिसेल की सरासरी चौरस त्रुटी जवळजवळ समान आहे, परंतु आम्हाला खूप उच्च निर्धारण गुणांक (~77%) मिळतो. अधिक अचूक अंदाज मिळवण्यासाठी, आम्ही अधिक श्रेणी वैशिष्ट्यांचा विचार करू शकतो, तसेच `Month` किंवा `DayOfYear` सारख्या न्यूमेरिक वैशिष्ट्यांचा विचार करू शकतो. एक मोठा वैशिष्ट्यांचा अ‍ॅरे मिळवण्यासाठी, आम्ही `join` वापरू शकतो: ```python X = pd.get_dummies(new_pumpkins['Variety']) \ .join(new_pumpkins['Month']) \ .join(pd.get_dummies(new_pumpkins['City'])) \ .join(pd.get_dummies(new_pumpkins['Package'])) y = new_pumpkins['Price'] ``` येथे आम्ही `City` आणि `Package` प्रकाराचाही विचार करतो, ज्यामुळे आम्हाला MSE 2.84 (10%) आणि निर्धारण 0.94 मिळते! ## सर्वकाही एकत्र ठेवणे सर्वात चांगले मॉडेल तयार करण्यासाठी, आम्ही वरील उदाहरणातील संयुक्त (वन-हॉट एन्कोड केलेले श्रेणी + न्यूमेरिक) डेटा बहुपद रिग्रेशनसह वापरू शकतो. तुमच्या सोयीसाठी येथे संपूर्ण कोड आहे: ```python # set up training data X = pd.get_dummies(new_pumpkins['Variety']) \ .join(new_pumpkins['Month']) \ .join(pd.get_dummies(new_pumpkins['City'])) \ .join(pd.get_dummies(new_pumpkins['Package'])) y = new_pumpkins['Price'] # make train-test split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) # setup and train the pipeline pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression()) pipeline.fit(X_train,y_train) # predict results for test data pred = pipeline.predict(X_test) # calculate MSE and determination mse = np.sqrt(mean_squared_error(y_test,pred)) print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)') score = pipeline.score(X_train,y_train) print('Model determination: ', score) ``` यामुळे आम्हाला जवळजवळ 97% निर्धारण गुणांक आणि MSE=2.23 (~8% अंदाज त्रुटी) मिळेल. | मॉडेल | MSE | निर्धारण | |-------|-----|----------| | `DayOfYear` रेषीय | 2.77 (17.2%) | 0.07 | | `DayOfYear` बहुपद | 2.73 (17.0%) | 0.08 | | `Variety` रेषीय | 5.24 (19.7%) | 0.77 | | सर्व वैशिष्ट्ये रेषीय | 2.84 (10.5%) | 0.94 | | सर्व वैशिष्ट्ये बहुपद | 2.23 (8.25%) | 0.97 | 🏆 उत्तम काम! तुम्ही एका धड्यात चार रिग्रेशन मॉडेल्स तयार केली आणि मॉडेलची गुणवत्ता 97% पर्यंत सुधारली. रिग्रेशनवरील अंतिम विभागात, तुम्ही श्रेणी निश्चित करण्यासाठी लॉजिस्टिक रिग्रेशनबद्दल शिकाल. --- ## 🚀चॅलेंज या नोटबुकमध्ये विविध व्हेरिएबल्स तपासा आणि पाहा की सहसंबंध मॉडेल अचूकतेशी कसा संबंधित आहे. ## [पाठ-व्याख्यान क्विझ](https://ff-quizzes.netlify.app/en/ml/) ## पुनरावलोकन आणि स्व-अभ्यास या धड्यात आपण रेषीय रिग्रेशनबद्दल शिकलो. रिग्रेशनचे इतर महत्त्वाचे प्रकार आहेत. Stepwise, Ridge, Lasso आणि Elasticnet तंत्रांबद्दल वाचा. अधिक शिकण्यासाठी एक चांगला अभ्यासक्रम म्हणजे [स्टॅनफोर्ड स्टॅटिस्टिकल लर्निंग कोर्स](https://online.stanford.edu/courses/sohs-ystatslearning-statistical-learning). ## असाइनमेंट [मॉडेल तयार करा](assignment.md) --- **अस्वीकरण**: हा दस्तऐवज AI भाषांतर सेवा [Co-op Translator](https://github.com/Azure/co-op-translator) चा वापर करून भाषांतरित करण्यात आला आहे. आम्ही अचूकतेसाठी प्रयत्नशील असलो तरी कृपया लक्षात घ्या की स्वयंचलित भाषांतरांमध्ये त्रुटी किंवा अचूकतेचा अभाव असू शकतो. मूळ भाषेतील दस्तऐवज हा अधिकृत स्रोत मानला जावा. महत्त्वाच्या माहितीसाठी व्यावसायिक मानवी भाषांतराची शिफारस केली जाते. या भाषांतराचा वापर केल्यामुळे उद्भवणाऱ्या कोणत्याही गैरसमज किंवा चुकीच्या अर्थासाठी आम्ही जबाबदार राहणार नाही.