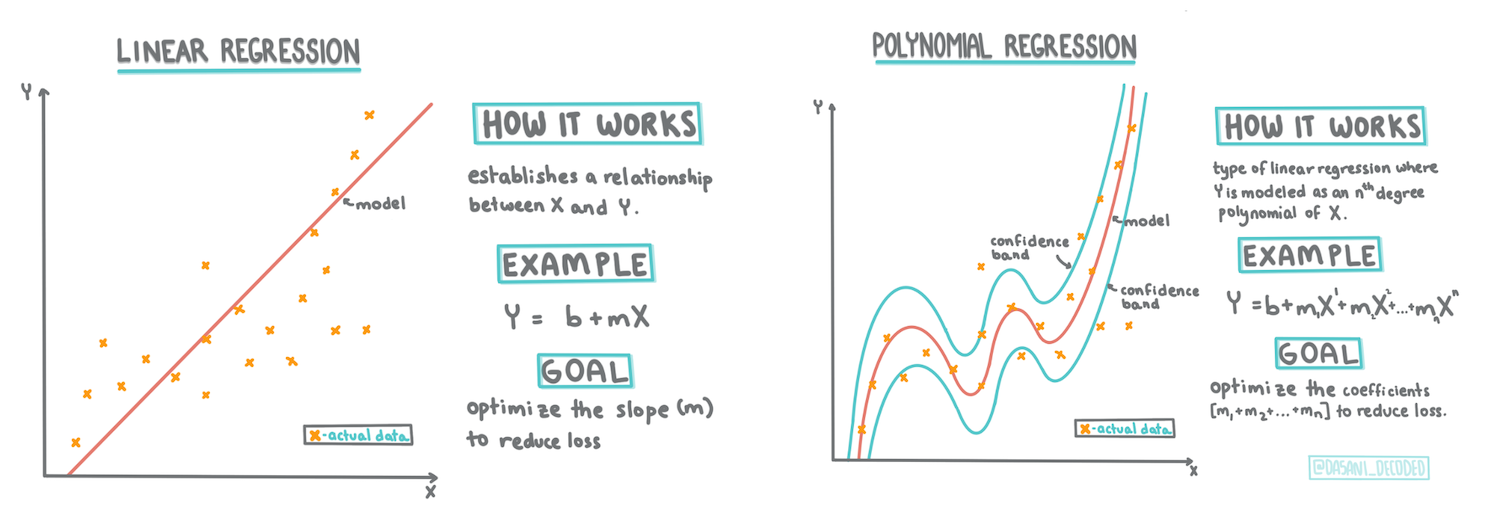
# Membangun Model Regresi Menggunakan Scikit-learn: Empat Cara Regresi  > Infografik oleh [Dasani Madipalli](https://twitter.com/dasani_decoded) ## [Kuis Pra-Pelajaran](https://ff-quizzes.netlify.app/en/ml/) > ### [Pelajaran ini tersedia dalam R!](../../../../2-Regression/3-Linear/solution/R/lesson_3.html) ### Pengantar Sejauh ini, Anda telah mempelajari apa itu regresi dengan data sampel yang diambil dari dataset harga labu yang akan kita gunakan sepanjang pelajaran ini. Anda juga telah memvisualisasikannya menggunakan Matplotlib. Sekarang Anda siap untuk mendalami regresi dalam pembelajaran mesin. Sementara visualisasi memungkinkan Anda memahami data, kekuatan sebenarnya dari Pembelajaran Mesin berasal dari _melatih model_. Model dilatih pada data historis untuk secara otomatis menangkap ketergantungan data, dan memungkinkan Anda memprediksi hasil untuk data baru yang belum pernah dilihat oleh model sebelumnya. Dalam pelajaran ini, Anda akan mempelajari lebih lanjut tentang dua jenis regresi: _regresi linear dasar_ dan _regresi polinomial_, bersama dengan beberapa matematika yang mendasari teknik-teknik ini. Model-model tersebut akan memungkinkan kita memprediksi harga labu berdasarkan berbagai data input. [](https://youtu.be/CRxFT8oTDMg "ML untuk pemula - Memahami Regresi Linear") > 🎥 Klik gambar di atas untuk video singkat tentang regresi linear. > Sepanjang kurikulum ini, kami mengasumsikan pengetahuan matematika yang minimal, dan berusaha membuatnya dapat diakses oleh siswa dari bidang lain, jadi perhatikan catatan, 🧮 penjelasan, diagram, dan alat pembelajaran lainnya untuk membantu pemahaman. ### Prasyarat Pada titik ini, Anda seharusnya sudah familiar dengan struktur data labu yang sedang kita analisis. Anda dapat menemukannya sudah dimuat dan dibersihkan di file _notebook.ipynb_ pelajaran ini. Dalam file tersebut, harga labu ditampilkan per bushel dalam kerangka data baru. Pastikan Anda dapat menjalankan notebook ini di kernel Visual Studio Code. ### Persiapan Sebagai pengingat, Anda memuat data ini untuk mengajukan pertanyaan tentangnya. - Kapan waktu terbaik untuk membeli labu? - Berapa harga yang bisa saya harapkan untuk satu kotak labu mini? - Haruskah saya membelinya dalam keranjang setengah bushel atau dalam kotak bushel 1 1/9? Mari kita terus menggali data ini. Dalam pelajaran sebelumnya, Anda membuat kerangka data Pandas dan mengisinya dengan sebagian dari dataset asli, menstandarkan harga berdasarkan bushel. Namun, dengan melakukan itu, Anda hanya dapat mengumpulkan sekitar 400 titik data dan hanya untuk bulan-bulan musim gugur. Lihat data yang telah dimuat sebelumnya di notebook yang menyertai pelajaran ini. Data telah dimuat sebelumnya dan plot sebar awal telah dibuat untuk menunjukkan data bulan. Mungkin kita bisa mendapatkan sedikit lebih banyak detail tentang sifat data dengan membersihkannya lebih lanjut. ## Garis Regresi Linear Seperti yang Anda pelajari di Pelajaran 1, tujuan dari latihan regresi linear adalah untuk dapat membuat garis untuk: - **Menunjukkan hubungan variabel**. Menunjukkan hubungan antara variabel - **Membuat prediksi**. Membuat prediksi yang akurat tentang di mana titik data baru akan berada dalam hubungan dengan garis tersebut. Biasanya, **Regresi Kuadrat Terkecil** digunakan untuk menggambar jenis garis ini. Istilah 'kuadrat terkecil' berarti bahwa semua titik data di sekitar garis regresi dikuadratkan dan kemudian dijumlahkan. Idealnya, jumlah akhir itu sekecil mungkin, karena kita menginginkan jumlah kesalahan yang rendah, atau `kuadrat terkecil`. Kami melakukan ini karena kami ingin memodelkan garis yang memiliki jarak kumulatif terkecil dari semua titik data kami. Kami juga mengkuadratkan istilah sebelum menjumlahkannya karena kami lebih peduli dengan besarnya daripada arahnya. 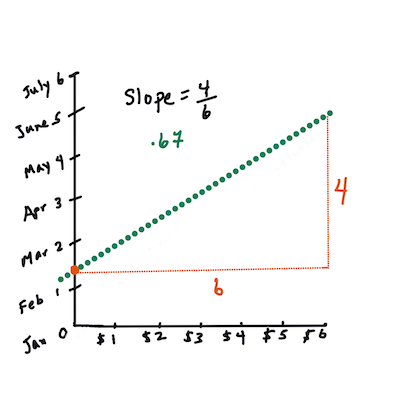> **🧮 Tunjukkan matematikanya** > > Garis ini, yang disebut _garis terbaik_, dapat diekspresikan dengan [persamaan](https://en.wikipedia.org/wiki/Simple_linear_regression): > > ``` > Y = a + bX > ``` > > `X` adalah 'variabel penjelas'. `Y` adalah 'variabel dependen'. Kemiringan garis adalah `b` dan `a` adalah titik potong sumbu y, yang mengacu pada nilai `Y` ketika `X = 0`. > > > > Pertama, hitung kemiringan `b`. 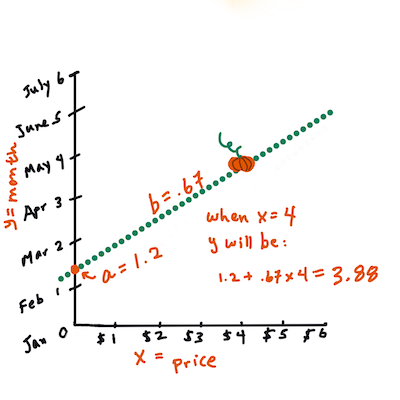Infografik oleh [Jen Looper](https://twitter.com/jenlooper) > > Dengan kata lain, dan merujuk pada pertanyaan asli data labu kita: "memprediksi harga labu per bushel berdasarkan bulan", `X` akan merujuk pada harga dan `Y` akan merujuk pada bulan penjualan. > > > > Hitung nilai Y. Jika Anda membayar sekitar $4, itu pasti bulan April! Infografik oleh [Jen Looper](https://twitter.com/jenlooper) > > Matematika yang menghitung garis harus menunjukkan kemiringan garis, yang juga bergantung pada titik potong, atau di mana `Y` berada ketika `X = 0`. > > Anda dapat mengamati metode perhitungan untuk nilai-nilai ini di situs web [Math is Fun](https://www.mathsisfun.com/data/least-squares-regression.html). Juga kunjungi [Kalkulator Kuadrat Terkecil](https://www.mathsisfun.com/data/least-squares-calculator.html) untuk melihat bagaimana nilai angka memengaruhi garis. ## Korelasi Satu istilah lagi yang perlu dipahami adalah **Koefisien Korelasi** antara variabel X dan Y yang diberikan. Menggunakan plot sebar, Anda dapat dengan cepat memvisualisasikan koefisien ini. Plot dengan titik data yang tersebar dalam garis rapi memiliki korelasi tinggi, tetapi plot dengan titik data yang tersebar di mana-mana antara X dan Y memiliki korelasi rendah. Model regresi linear yang baik adalah model yang memiliki Koefisien Korelasi tinggi (lebih dekat ke 1 daripada 0) menggunakan metode Regresi Kuadrat Terkecil dengan garis regresi. ✅ Jalankan notebook yang menyertai pelajaran ini dan lihat plot sebar Bulan ke Harga. Apakah data yang menghubungkan Bulan ke Harga untuk penjualan labu tampaknya memiliki korelasi tinggi atau rendah, menurut interpretasi visual Anda terhadap plot sebar? Apakah itu berubah jika Anda menggunakan ukuran yang lebih rinci daripada `Bulan`, misalnya *hari dalam setahun* (yaitu jumlah hari sejak awal tahun)? Dalam kode di bawah ini, kita akan mengasumsikan bahwa kita telah membersihkan data, dan memperoleh kerangka data yang disebut `new_pumpkins`, mirip dengan berikut ini: ID | Bulan | HariDalamTahun | Jenis | Kota | Paket | Harga Rendah | Harga Tinggi | Harga ---|-------|----------------|-------|------|-------|--------------|--------------|------ 70 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 15.0 | 15.0 | 13.636364 71 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 18.0 | 18.0 | 16.363636 72 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 18.0 | 18.0 | 16.363636 73 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 17.0 | 17.0 | 15.454545 74 | 10 | 281 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 15.0 | 15.0 | 13.636364 > Kode untuk membersihkan data tersedia di [`notebook.ipynb`](../../../../2-Regression/3-Linear/notebook.ipynb). Kami telah melakukan langkah-langkah pembersihan yang sama seperti pada pelajaran sebelumnya, dan telah menghitung kolom `HariDalamTahun` menggunakan ekspresi berikut: ```python day_of_year = pd.to_datetime(pumpkins['Date']).apply(lambda dt: (dt-datetime(dt.year,1,1)).days) ``` Sekarang setelah Anda memahami matematika di balik regresi linear, mari kita buat model Regresi untuk melihat apakah kita dapat memprediksi paket labu mana yang akan memiliki harga labu terbaik. Seseorang yang membeli labu untuk kebun labu liburan mungkin menginginkan informasi ini untuk dapat mengoptimalkan pembelian paket labu untuk kebun tersebut. ## Mencari Korelasi [](https://youtu.be/uoRq-lW2eQo "ML untuk pemula - Mencari Korelasi: Kunci Regresi Linear") > 🎥 Klik gambar di atas untuk video singkat tentang korelasi. Dari pelajaran sebelumnya, Anda mungkin telah melihat bahwa harga rata-rata untuk berbagai bulan terlihat seperti ini: Ini menunjukkan bahwa seharusnya ada beberapa korelasi, dan kita dapat mencoba melatih model regresi linear untuk memprediksi hubungan antara `Bulan` dan `Harga`, atau antara `HariDalamTahun` dan `Harga`. Berikut adalah plot sebar yang menunjukkan hubungan yang terakhir: Mari kita lihat apakah ada korelasi menggunakan fungsi `corr`: ```python print(new_pumpkins['Month'].corr(new_pumpkins['Price'])) print(new_pumpkins['DayOfYear'].corr(new_pumpkins['Price'])) ``` Tampaknya korelasi cukup kecil, -0.15 berdasarkan `Bulan` dan -0.17 berdasarkan `HariDalamTahun`, tetapi mungkin ada hubungan penting lainnya. Tampaknya ada kelompok harga yang berbeda yang sesuai dengan berbagai jenis labu. Untuk mengonfirmasi hipotesis ini, mari kita plot setiap kategori labu menggunakan warna yang berbeda. Dengan meneruskan parameter `ax` ke fungsi plot sebar, kita dapat memplot semua titik pada grafik yang sama: ```python ax=None colors = ['red','blue','green','yellow'] for i,var in enumerate(new_pumpkins['Variety'].unique()): df = new_pumpkins[new_pumpkins['Variety']==var] ax = df.plot.scatter('DayOfYear','Price',ax=ax,c=colors[i],label=var) ``` Penyelidikan kami menunjukkan bahwa jenis labu memiliki pengaruh lebih besar pada harga keseluruhan daripada tanggal penjualan sebenarnya. Kita dapat melihat ini dengan grafik batang: ```python new_pumpkins.groupby('Variety')['Price'].mean().plot(kind='bar') ``` Mari kita fokus untuk sementara hanya pada satu jenis labu, yaitu 'pie type', dan lihat apa pengaruh tanggal terhadap harga: ```python pie_pumpkins = new_pumpkins[new_pumpkins['Variety']=='PIE TYPE'] pie_pumpkins.plot.scatter('DayOfYear','Price') ``` Jika kita sekarang menghitung korelasi antara `Harga` dan `HariDalamTahun` menggunakan fungsi `corr`, kita akan mendapatkan sesuatu seperti `-0.27` - yang berarti bahwa melatih model prediktif masuk akal. > Sebelum melatih model regresi linear, penting untuk memastikan bahwa data kita bersih. Regresi linear tidak bekerja dengan baik dengan nilai yang hilang, sehingga masuk akal untuk menghapus semua sel kosong: ```python pie_pumpkins.dropna(inplace=True) pie_pumpkins.info() ``` Pendekatan lain adalah mengisi nilai kosong tersebut dengan nilai rata-rata dari kolom yang sesuai. ## Regresi Linear Sederhana [](https://youtu.be/e4c_UP2fSjg "ML untuk pemula - Regresi Linear dan Polinomial menggunakan Scikit-learn") > 🎥 Klik gambar di atas untuk video singkat tentang regresi linear dan polinomial. Untuk melatih model Regresi Linear kita, kita akan menggunakan pustaka **Scikit-learn**. ```python from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error from sklearn.model_selection import train_test_split ``` Kita mulai dengan memisahkan nilai input (fitur) dan output yang diharapkan (label) ke dalam array numpy terpisah: ```python X = pie_pumpkins['DayOfYear'].to_numpy().reshape(-1,1) y = pie_pumpkins['Price'] ``` > Perhatikan bahwa kita harus melakukan `reshape` pada data input agar paket Regresi Linear dapat memahaminya dengan benar. Regresi Linear mengharapkan array 2D sebagai input, di mana setiap baris array sesuai dengan vektor fitur input. Dalam kasus kita, karena kita hanya memiliki satu input - kita membutuhkan array dengan bentuk N×1, di mana N adalah ukuran dataset. Kemudian, kita perlu membagi data menjadi dataset pelatihan dan pengujian, sehingga kita dapat memvalidasi model kita setelah pelatihan: ```python X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) ``` Akhirnya, melatih model Regresi Linear yang sebenarnya hanya membutuhkan dua baris kode. Kita mendefinisikan objek `LinearRegression`, dan menyesuaikannya dengan data kita menggunakan metode `fit`: ```python lin_reg = LinearRegression() lin_reg.fit(X_train,y_train) ``` Objek `LinearRegression` setelah `fit`-ting berisi semua koefisien regresi, yang dapat diakses menggunakan properti `.coef_`. Dalam kasus kita, hanya ada satu koefisien, yang seharusnya sekitar `-0.017`. Ini berarti bahwa harga tampaknya turun sedikit seiring waktu, tetapi tidak terlalu banyak, sekitar 2 sen per hari. Kita juga dapat mengakses titik perpotongan regresi dengan sumbu Y menggunakan `lin_reg.intercept_` - ini akan sekitar `21` dalam kasus kita, menunjukkan harga di awal tahun. Untuk melihat seberapa akurat model kita, kita dapat memprediksi harga pada dataset pengujian, dan kemudian mengukur seberapa dekat prediksi kita dengan nilai yang diharapkan. Ini dapat dilakukan menggunakan metrik mean square error (MSE), yang merupakan rata-rata dari semua perbedaan kuadrat antara nilai yang diharapkan dan nilai yang diprediksi. ```python pred = lin_reg.predict(X_test) mse = np.sqrt(mean_squared_error(y_test,pred)) print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)') ``` Kesalahan kita tampaknya berada di sekitar 2 poin, yaitu ~17%. Tidak terlalu bagus. Indikator lain dari kualitas model adalah **koefisien determinasi**, yang dapat diperoleh seperti ini: ```python score = lin_reg.score(X_train,y_train) print('Model determination: ', score) ``` Jika nilainya 0, itu berarti model tidak mempertimbangkan data input, dan bertindak sebagai *prediktor linear terburuk*, yang hanya merupakan nilai rata-rata dari hasil. Nilai 1 berarti kita dapat memprediksi semua output yang diharapkan dengan sempurna. Dalam kasus kita, koefisiennya sekitar 0.06, yang cukup rendah. Kita juga dapat memplot data uji bersama dengan garis regresi untuk melihat lebih jelas bagaimana regresi bekerja dalam kasus kita: ```python plt.scatter(X_test,y_test) plt.plot(X_test,pred) ``` ## Regresi Polinomial Jenis lain dari Regresi Linear adalah Regresi Polinomial. Meskipun terkadang ada hubungan linear antara variabel - semakin besar volume labu, semakin tinggi harganya - terkadang hubungan ini tidak dapat dipetakan sebagai bidang atau garis lurus. ✅ Berikut adalah [beberapa contoh lainnya](https://online.stat.psu.edu/stat501/lesson/9/9.8) dari data yang dapat menggunakan Regresi Polinomial. Lihat kembali hubungan antara Tanggal dan Harga. Apakah scatterplot ini tampaknya harus dianalisis dengan garis lurus? Bukankah harga bisa berfluktuasi? Dalam kasus ini, Anda dapat mencoba regresi polinomial. ✅ Polinomial adalah ekspresi matematika yang mungkin terdiri dari satu atau lebih variabel dan koefisien. Regresi polinomial menciptakan garis melengkung untuk lebih cocok dengan data non-linear. Dalam kasus kita, jika kita menyertakan variabel `DayOfYear` kuadrat ke dalam data input, kita harus dapat menyesuaikan data kita dengan kurva parabola, yang akan memiliki titik minimum pada waktu tertentu dalam setahun. Scikit-learn menyertakan [API pipeline](https://scikit-learn.org/stable/modules/generated/sklearn.pipeline.make_pipeline.html?highlight=pipeline#sklearn.pipeline.make_pipeline) yang berguna untuk menggabungkan berbagai langkah pemrosesan data. **Pipeline** adalah rantai **estimasi**. Dalam kasus kita, kita akan membuat pipeline yang pertama-tama menambahkan fitur polinomial ke model kita, lalu melatih regresi: ```python from sklearn.preprocessing import PolynomialFeatures from sklearn.pipeline import make_pipeline pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression()) pipeline.fit(X_train,y_train) ``` Menggunakan `PolynomialFeatures(2)` berarti kita akan menyertakan semua polinomial derajat kedua dari data input. Dalam kasus kita, ini hanya berarti `DayOfYear`², tetapi dengan dua variabel input X dan Y, ini akan menambahkan X², XY, dan Y². Kita juga dapat menggunakan polinomial derajat lebih tinggi jika diinginkan. Pipeline dapat digunakan dengan cara yang sama seperti objek `LinearRegression` asli, yaitu kita dapat `fit` pipeline, lalu menggunakan `predict` untuk mendapatkan hasil prediksi. Berikut adalah grafik yang menunjukkan data uji dan kurva aproksimasi: Dengan menggunakan Regresi Polinomial, kita dapat memperoleh MSE yang sedikit lebih rendah dan determinasi yang lebih tinggi, tetapi tidak signifikan. Kita perlu mempertimbangkan fitur lainnya! > Anda dapat melihat bahwa harga labu terendah diamati di sekitar Halloween. Bagaimana Anda menjelaskan ini? 🎃 Selamat, Anda baru saja membuat model yang dapat membantu memprediksi harga labu untuk pai. Anda mungkin dapat mengulangi prosedur yang sama untuk semua jenis labu, tetapi itu akan membosankan. Sekarang mari kita pelajari cara mempertimbangkan variasi labu dalam model kita! ## Fitur Kategorikal Dalam dunia ideal, kita ingin dapat memprediksi harga untuk berbagai jenis labu menggunakan model yang sama. Namun, kolom `Variety` agak berbeda dari kolom seperti `Month`, karena berisi nilai non-numerik. Kolom seperti ini disebut **kategorikal**. [](https://youtu.be/DYGliioIAE0 "ML untuk pemula - Prediksi Fitur Kategorikal dengan Regresi Linear") > 🎥 Klik gambar di atas untuk video singkat tentang penggunaan fitur kategorikal. Di sini Anda dapat melihat bagaimana harga rata-rata bergantung pada variasi: Untuk mempertimbangkan variasi, pertama-tama kita perlu mengonversinya ke bentuk numerik, atau **encode**. Ada beberapa cara untuk melakukannya: * **Numeric encoding** sederhana akan membuat tabel variasi yang berbeda, lalu mengganti nama variasi dengan indeks dalam tabel tersebut. Ini bukan ide terbaik untuk regresi linear, karena regresi linear mengambil nilai numerik aktual dari indeks dan menambahkannya ke hasil, mengalikan dengan beberapa koefisien. Dalam kasus kita, hubungan antara nomor indeks dan harga jelas tidak linear, bahkan jika kita memastikan bahwa indeks diurutkan dengan cara tertentu. * **One-hot encoding** akan mengganti kolom `Variety` dengan 4 kolom berbeda, satu untuk setiap variasi. Setiap kolom akan berisi `1` jika baris yang sesuai adalah variasi tertentu, dan `0` jika tidak. Ini berarti akan ada empat koefisien dalam regresi linear, satu untuk setiap variasi labu, yang bertanggung jawab atas "harga awal" (atau lebih tepatnya "harga tambahan") untuk variasi tertentu. Kode di bawah ini menunjukkan bagaimana kita dapat melakukan one-hot encoding pada variasi: ```python pd.get_dummies(new_pumpkins['Variety']) ``` ID | FAIRYTALE | MINIATURE | MIXED HEIRLOOM VARIETIES | PIE TYPE ----|-----------|-----------|--------------------------|---------- 70 | 0 | 0 | 0 | 1 71 | 0 | 0 | 0 | 1 ... | ... | ... | ... | ... 1738 | 0 | 1 | 0 | 0 1739 | 0 | 1 | 0 | 0 1740 | 0 | 1 | 0 | 0 1741 | 0 | 1 | 0 | 0 1742 | 0 | 1 | 0 | 0 Untuk melatih regresi linear menggunakan variasi yang telah di-one-hot encode sebagai input, kita hanya perlu menginisialisasi data `X` dan `y` dengan benar: ```python X = pd.get_dummies(new_pumpkins['Variety']) y = new_pumpkins['Price'] ``` Sisa kode sama seperti yang kita gunakan di atas untuk melatih Regresi Linear. Jika Anda mencobanya, Anda akan melihat bahwa mean squared error hampir sama, tetapi kita mendapatkan koefisien determinasi yang jauh lebih tinggi (~77%). Untuk mendapatkan prediksi yang lebih akurat, kita dapat mempertimbangkan lebih banyak fitur kategorikal, serta fitur numerik seperti `Month` atau `DayOfYear`. Untuk mendapatkan satu array besar fitur, kita dapat menggunakan `join`: ```python X = pd.get_dummies(new_pumpkins['Variety']) \ .join(new_pumpkins['Month']) \ .join(pd.get_dummies(new_pumpkins['City'])) \ .join(pd.get_dummies(new_pumpkins['Package'])) y = new_pumpkins['Price'] ``` Di sini kita juga mempertimbangkan `City` dan jenis `Package`, yang memberikan kita MSE 2.84 (10%), dan determinasi 0.94! ## Menggabungkan Semuanya Untuk membuat model terbaik, kita dapat menggunakan data gabungan (one-hot encoded kategorikal + numerik) dari contoh di atas bersama dengan Regresi Polinomial. Berikut adalah kode lengkap untuk kenyamanan Anda: ```python # set up training data X = pd.get_dummies(new_pumpkins['Variety']) \ .join(new_pumpkins['Month']) \ .join(pd.get_dummies(new_pumpkins['City'])) \ .join(pd.get_dummies(new_pumpkins['Package'])) y = new_pumpkins['Price'] # make train-test split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) # setup and train the pipeline pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression()) pipeline.fit(X_train,y_train) # predict results for test data pred = pipeline.predict(X_test) # calculate MSE and determination mse = np.sqrt(mean_squared_error(y_test,pred)) print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)') score = pipeline.score(X_train,y_train) print('Model determination: ', score) ``` Ini seharusnya memberikan kita koefisien determinasi terbaik hampir 97%, dan MSE=2.23 (~8% kesalahan prediksi). | Model | MSE | Determinasi | |-------|-----|-------------| | `DayOfYear` Linear | 2.77 (17.2%) | 0.07 | | `DayOfYear` Polynomial | 2.73 (17.0%) | 0.08 | | `Variety` Linear | 5.24 (19.7%) | 0.77 | | Semua fitur Linear | 2.84 (10.5%) | 0.94 | | Semua fitur Polynomial | 2.23 (8.25%) | 0.97 | 🏆 Kerja bagus! Anda telah membuat empat model Regresi dalam satu pelajaran, dan meningkatkan kualitas model hingga 97%. Dalam bagian terakhir tentang Regresi, Anda akan belajar tentang Regresi Logistik untuk menentukan kategori. --- ## 🚀Tantangan Uji beberapa variabel berbeda dalam notebook ini untuk melihat bagaimana korelasi berhubungan dengan akurasi model. ## [Kuis setelah pelajaran](https://ff-quizzes.netlify.app/en/ml/) ## Tinjauan & Studi Mandiri Dalam pelajaran ini kita belajar tentang Regresi Linear. Ada jenis Regresi penting lainnya. Bacalah tentang teknik Stepwise, Ridge, Lasso, dan Elasticnet. Kursus yang bagus untuk mempelajari lebih lanjut adalah [Kursus Pembelajaran Statistik Stanford](https://online.stanford.edu/courses/sohs-ystatslearning-statistical-learning). ## Tugas [Bangun Model](assignment.md) --- **Penafian**: Dokumen ini telah diterjemahkan menggunakan layanan penerjemahan AI [Co-op Translator](https://github.com/Azure/co-op-translator). Meskipun kami berusaha untuk memberikan hasil yang akurat, harap diketahui bahwa terjemahan otomatis mungkin mengandung kesalahan atau ketidakakuratan. Dokumen asli dalam bahasa aslinya harus dianggap sebagai sumber yang otoritatif. Untuk informasi yang bersifat kritis, disarankan menggunakan jasa penerjemahan profesional oleh manusia. Kami tidak bertanggung jawab atas kesalahpahaman atau penafsiran yang keliru yang timbul dari penggunaan terjemahan ini.