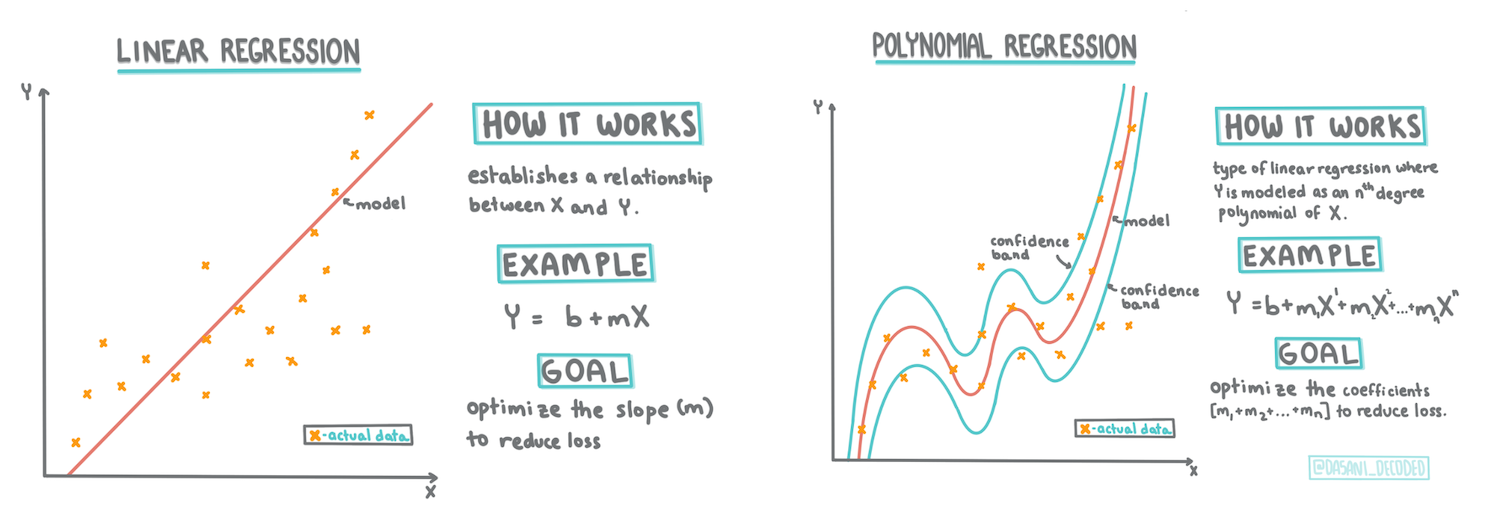
# Készítsünk regressziós modellt Scikit-learn segítségével: négyféle regresszió  > Infografika: [Dasani Madipalli](https://twitter.com/dasani_decoded) ## [Előadás előtti kvíz](https://ff-quizzes.netlify.app/en/ml/) > ### [Ez a lecke elérhető R-ben is!](../../../../2-Regression/3-Linear/solution/R/lesson_3.html) ### Bevezetés Eddig megismerkedtél azzal, hogy mi is az a regresszió, például a tökárak adatain keresztül, amelyeket ebben a leckében fogunk használni. A Matplotlib segítségével vizualizáltad is az adatokat. Most készen állsz arra, hogy mélyebben belemerülj a gépi tanulás regressziós technikáiba. Bár a vizualizáció segít az adatok megértésében, a gépi tanulás valódi ereje a _modellek tanításában_ rejlik. A modelleket történelmi adatokon tanítjuk, hogy automatikusan felismerjék az adatok közötti összefüggéseket, és lehetővé tegyék az előrejelzést olyan új adatokra, amelyeket a modell korábban nem látott. Ebben a leckében többet fogsz megtudni kétféle regresszióról: _egyszerű lineáris regresszióról_ és _polinomiális regresszióról_, valamint az ezek mögött álló matematikáról. Ezek a modellek lehetővé teszik számunkra, hogy különböző bemeneti adatok alapján előre jelezzük a tökárakat. [](https://youtu.be/CRxFT8oTDMg "Gépi tanulás kezdőknek - A lineáris regresszió megértése") > 🎥 Kattints a fenti képre egy rövid videós összefoglalóért a lineáris regresszióról. > Ebben a tananyagban minimális matematikai ismereteket feltételezünk, és igyekszünk hozzáférhetővé tenni a különböző területekről érkező diákok számára. Figyelj a jegyzetekre, 🧮 matematikai hívásokra, diagramokra és más tanulási eszközökre, amelyek segítik a megértést. ### Előfeltétel Mostanra már ismerned kell a tökadatok szerkezetét, amelyeket vizsgálunk. Ezek az adatok előre betöltve és megtisztítva találhatók meg ennek a leckének a _notebook.ipynb_ fájljában. A fájlban a tökárak bushelre vetítve jelennek meg egy új adatkeretben. Győződj meg róla, hogy ezeket a notebookokat futtatni tudod a Visual Studio Code kerneljeiben. ### Felkészülés Emlékeztetőül: ezeket az adatokat azért töltöd be, hogy kérdéseket tegyél fel velük kapcsolatban. - Mikor érdemes tököt vásárolni? - Milyen árat várhatok egy doboz miniatűr tök esetében? - Érdemes fél bushel kosárban vagy 1 1/9 bushel dobozban vásárolni őket? Folytassuk az adatok vizsgálatát. Az előző leckében létrehoztál egy Pandas adatkeretet, és feltöltötted az eredeti adatkészlet egy részével, standardizálva az árakat bushelre vetítve. Ezzel azonban csak körülbelül 400 adatpontot tudtál összegyűjteni, és csak az őszi hónapokra vonatkozóan. Nézd meg az adatokat, amelyeket előre betöltöttünk ennek a leckének a notebookjában. Az adatok előre betöltve vannak, és egy kezdeti szórásdiagramot is készítettünk, amely hónap adatokat mutat. Talán egy kicsit részletesebb képet kaphatunk az adatok természetéről, ha tovább tisztítjuk őket. ## Egy lineáris regressziós vonal Ahogy az 1. leckében megtanultad, a lineáris regresszió célja, hogy egy vonalat rajzoljunk, amely: - **Megmutatja a változók közötti kapcsolatot**. Megmutatja a változók közötti összefüggést. - **Előrejelzéseket készít**. Pontos előrejelzéseket készít arról, hogy egy új adatpont hol helyezkedne el a vonalhoz képest. A **Legkisebb négyzetek regressziója** általában ezt a fajta vonalat rajzolja. A "legkisebb négyzetek" kifejezés azt jelenti, hogy a regressziós vonal körüli összes adatpontot négyzetre emeljük, majd összeadjuk. Ideális esetben ez az összeg a lehető legkisebb, mivel alacsony hibaszámot, vagyis `legkisebb négyzeteket` szeretnénk. Ezt azért tesszük, mert olyan vonalat szeretnénk modellezni, amelynek a legkisebb kumulatív távolsága van az összes adatponttól. Az értékeket négyzetre emeljük, mielőtt összeadnánk őket, mivel az irány helyett a nagyságuk érdekel minket. 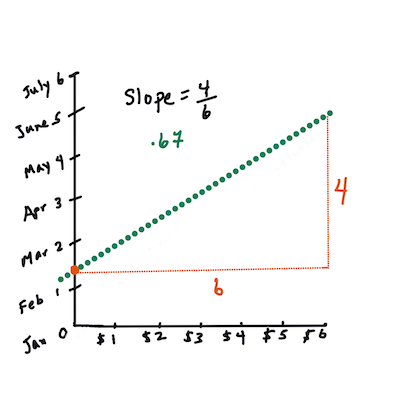> **🧮 Mutasd a matematikát** > > Ez a vonal, amelyet _legjobb illeszkedés vonalának_ nevezünk, [egy egyenlettel](https://en.wikipedia.org/wiki/Simple_linear_regression) fejezhető ki: > > ``` > Y = a + bX > ``` > > `X` az 'magyarázó változó'. `Y` a 'függő változó'. A vonal meredeksége `b`, és `a` az y-metszet, amely arra utal, hogy `Y` értéke mennyi, amikor `X = 0`. > > > > Először számítsd ki a meredekséget `b`. Infografika: [Jen Looper](https://twitter.com/jenlooper) > > Más szavakkal, és utalva a tökadatok eredeti kérdésére: "jósoljuk meg a tök árát bushelre vetítve hónap szerint", `X` az árra, `Y` pedig az eladási hónapra utalna. 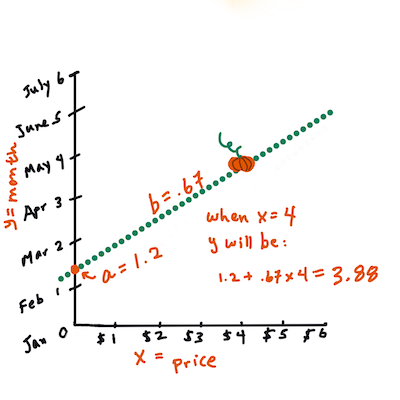> > > > Számítsd ki `Y` értékét. Ha körülbelül 4 dollárt fizetsz, akkor április van! Infografika: [Jen Looper](https://twitter.com/jenlooper) > > Az egyenlet kiszámításához szükséges matematika megmutatja a vonal meredekségét, amely az y-metszettől is függ, vagyis attól, hogy `Y` hol helyezkedik el, amikor `X = 0`. > > Megfigyelheted az értékek kiszámításának módszerét a [Math is Fun](https://www.mathsisfun.com/data/least-squares-regression.html) weboldalon. Látogasd meg a [Legkisebb négyzetek kalkulátort](https://www.mathsisfun.com/data/least-squares-calculator.html), hogy láthasd, hogyan befolyásolják a számok értékei a vonalat. ## Korreláció Egy másik fontos fogalom a **Korrelációs együttható** az adott X és Y változók között. Egy szórásdiagram segítségével gyorsan vizualizálhatod ezt az együtthatót. Ha az adatpontok szépen egy vonalban helyezkednek el, akkor magas korrelációról beszélünk, de ha az adatpontok szétszórtan helyezkednek el X és Y között, akkor alacsony korrelációról van szó. Egy jó lineáris regressziós modell olyan, amelynek magas (1-hez közelebb álló, mint 0-hoz) Korrelációs együtthatója van a Legkisebb négyzetek regressziós módszerével és egy regressziós vonallal. ✅ Futtasd a leckéhez tartozó notebookot, és nézd meg a Hónap és Ár szórásdiagramot. Az adatok, amelyek a Hónap és Ár közötti kapcsolatot mutatják a tökeladások esetében, vizuális értelmezésed szerint magas vagy alacsony korrelációval rendelkeznek? Változik ez, ha finomabb mértéket használsz a `Hónap` helyett, például *az év napját* (azaz az év eleje óta eltelt napok száma)? Az alábbi kódban feltételezzük, hogy megtisztítottuk az adatokat, és egy `new_pumpkins` nevű adatkeretet kaptunk, amely hasonló az alábbihoz: ID | Hónap | ÉvNapja | Fajta | Város | Csomagolás | Alacsony ár | Magas ár | Ár ---|-------|---------|-------|-------|------------|-------------|----------|----- 70 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 bushel kartonok | 15.0 | 15.0 | 13.636364 71 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 bushel kartonok | 18.0 | 18.0 | 16.363636 72 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 bushel kartonok | 18.0 | 18.0 | 16.363636 73 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 bushel kartonok | 17.0 | 17.0 | 15.454545 74 | 10 | 281 | PIE TYPE | BALTIMORE | 1 1/9 bushel kartonok | 15.0 | 15.0 | 13.636364 > Az adatok tisztításához szükséges kód megtalálható a [`notebook.ipynb`](../../../../2-Regression/3-Linear/notebook.ipynb) fájlban. Ugyanazokat a tisztítási lépéseket hajtottuk végre, mint az előző leckében, és kiszámítottuk az `ÉvNapja` oszlopot az alábbi kifejezés segítségével: ```python day_of_year = pd.to_datetime(pumpkins['Date']).apply(lambda dt: (dt-datetime(dt.year,1,1)).days) ``` Most, hogy megértetted a lineáris regresszió mögötti matematikát, hozzunk létre egy regressziós modellt, hogy megnézzük, meg tudjuk-e jósolni, melyik tökcsomagolás kínálja a legjobb árakat. Valaki, aki tököt vásárol egy ünnepi tökfolt számára, szeretné optimalizálni a tökcsomagok vásárlását. ## Korreláció keresése [](https://youtu.be/uoRq-lW2eQo "Gépi tanulás kezdőknek - Korreláció keresése: A lineáris regresszió kulcsa") > 🎥 Kattints a fenti képre egy rövid videós összefoglalóért a korrelációról. Az előző leckéből valószínűleg láttad, hogy az átlagár különböző hónapokra így néz ki: Ez arra utal, hogy lehet némi korreláció, és megpróbálhatunk egy lineáris regressziós modellt tanítani, hogy megjósoljuk a `Hónap` és `Ár`, vagy az `ÉvNapja` és `Ár` közötti kapcsolatot. Íme egy szórásdiagram, amely az utóbbi kapcsolatot mutatja: Nézzük meg, van-e korreláció a `corr` függvény segítségével: ```python print(new_pumpkins['Month'].corr(new_pumpkins['Price'])) print(new_pumpkins['DayOfYear'].corr(new_pumpkins['Price'])) ``` Úgy tűnik, hogy a korreláció elég kicsi, -0.15 a `Hónap` és -0.17 az `ÉvNapja` esetében, de lehet, hogy van egy másik fontos kapcsolat. Úgy tűnik, hogy az árak különböző csoportjai a tökfajtákhoz kapcsolódnak. Ennek a hipotézisnek a megerősítéséhez ábrázoljuk minden tökkategóriát különböző színnel. Az `ax` paraméter átadásával a `scatter` ábrázolási függvénynek az összes pontot ugyanazon a grafikonon ábrázolhatjuk: ```python ax=None colors = ['red','blue','green','yellow'] for i,var in enumerate(new_pumpkins['Variety'].unique()): df = new_pumpkins[new_pumpkins['Variety']==var] ax = df.plot.scatter('DayOfYear','Price',ax=ax,c=colors[i],label=var) ``` Vizsgálatunk azt sugallja, hogy a fajta nagyobb hatással van az árakra, mint az eladási dátum. Ezt egy oszlopdiagramon is láthatjuk: ```python new_pumpkins.groupby('Variety')['Price'].mean().plot(kind='bar') ``` Most koncentráljunk egyetlen tökfajtára, a 'pie type'-ra, és nézzük meg, milyen hatással van a dátum az árra: ```python pie_pumpkins = new_pumpkins[new_pumpkins['Variety']=='PIE TYPE'] pie_pumpkins.plot.scatter('DayOfYear','Price') ``` Ha most kiszámítjuk az `Ár` és az `ÉvNapja` közötti korrelációt a `corr` függvény segítségével, körülbelül `-0.27` értéket kapunk - ami azt jelenti, hogy érdemes egy prediktív modellt tanítani. > Mielőtt lineáris regressziós modellt tanítanánk, fontos megbizonyosodni arról, hogy az adataink tiszták. A lineáris regresszió nem működik jól hiányzó értékekkel, ezért érdemes megszabadulni az üres celláktól: ```python pie_pumpkins.dropna(inplace=True) pie_pumpkins.info() ``` Egy másik megközelítés az lenne, hogy az üres értékeket az adott oszlop átlagértékeivel töltjük ki. ## Egyszerű lineáris regresszió [](https://youtu.be/e4c_UP2fSjg "Gépi tanulás kezdőknek - Lineáris és polinomiális regresszió Scikit-learn segítségével") > 🎥 Kattints a fenti képre egy rövid videós összefoglalóért a lineáris és polinomiális regresszióról. A lineáris regressziós modellünk tanításához a **Scikit-learn** könyvtárat fogjuk használni. ```python from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error from sklearn.model_selection import train_test_split ``` Először szétválasztjuk a bemeneti értékeket (jellemzők) és a várt kimenetet (címke) külön numpy tömbökbe: ```python X = pie_pumpkins['DayOfYear'].to_numpy().reshape(-1,1) y = pie_pumpkins['Price'] ``` > Figyeld meg, hogy a bemeneti adatokat `reshape`-el kellett átalakítanunk, hogy a Lineáris Regresszió csomag helyesen értelmezze. A Lineáris Regresszió 2D-tömböt vár bemenetként, ahol a tömb minden sora a bemeneti jellemzők vektorának felel meg. Ebben az esetben, mivel csak egy bemenetünk van, egy N×1 alakú tömbre van szükségünk, ahol N az adatkészlet mérete. Ezután az adatokat szét kell osztanunk tanító és teszt adatkészletekre, hogy a modellünket validálni tudjuk a tanítás után: ```python X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) ``` Végül a tényleges Lineáris Regressziós modell tanítása mindössze két kódsort igényel. Meghatározzuk a `LinearRegression` objektumot, és az adatainkra illesztjük a `fit` metódus segítségével: ```python lin_reg = LinearRegression() lin_reg.fit(X_train,y_train) ``` A `LinearRegression` objektum a `fit`-elés után tartalmazza a regresszió összes együtthatóját, amelyeket a `.coef_` tulajdonságon keresztül érhetünk el. Ebben az esetben csak egy együttható van, amelynek értéke Hibánk körülbelül 2 pontnál van, ami ~17%. Nem túl jó. Egy másik mutató a modell minőségére a **determinizációs együttható**, amelyet így lehet kiszámítani: ```python score = lin_reg.score(X_train,y_train) print('Model determination: ', score) ``` Ha az érték 0, az azt jelenti, hogy a modell nem veszi figyelembe a bemeneti adatokat, és úgy működik, mint a *legrosszabb lineáris előrejelző*, amely egyszerűen az eredmény átlagértéke. Az 1-es érték azt jelenti, hogy tökéletesen meg tudjuk jósolni az összes várt kimenetet. Esetünkben az együttható körülbelül 0.06, ami elég alacsony. A tesztadatokat a regressziós vonallal együtt is ábrázolhatjuk, hogy jobban lássuk, hogyan működik a regresszió a mi esetünkben: ```python plt.scatter(X_test,y_test) plt.plot(X_test,pred) ``` ## Polinomiális regresszió A lineáris regresszió egy másik típusa a polinomiális regresszió. Bár néha van lineáris kapcsolat a változók között – például minél nagyobb a tök térfogata, annál magasabb az ára –, néha ezek a kapcsolatok nem ábrázolhatók síkként vagy egyenes vonalként. ✅ Itt van [néhány példa](https://online.stat.psu.edu/stat501/lesson/9/9.8) olyan adatokra, amelyekhez polinomiális regressziót lehet használni. Nézd meg újra a dátum és az ár közötti kapcsolatot. Úgy tűnik, hogy ezt a szórásdiagramot feltétlenül egy egyenes vonallal kellene elemezni? Nem ingadozhatnak az árak? Ebben az esetben megpróbálhatod a polinomiális regressziót. ✅ A polinomok olyan matematikai kifejezések, amelyek egy vagy több változót és együtthatót tartalmazhatnak. A polinomiális regresszió egy görbe vonalat hoz létre, amely jobban illeszkedik a nemlineáris adatokhoz. Esetünkben, ha egy négyzetes `DayOfYear` változót is hozzáadunk a bemeneti adatokhoz, akkor egy parabola görbével tudjuk illeszteni az adatainkat, amelynek minimuma az év egy bizonyos pontján lesz. A Scikit-learn tartalmaz egy hasznos [pipeline API-t](https://scikit-learn.org/stable/modules/generated/sklearn.pipeline.make_pipeline.html?highlight=pipeline#sklearn.pipeline.make_pipeline), amely lehetővé teszi az adatfeldolgozás különböző lépéseinek összekapcsolását. A **pipeline** egy **becslők** láncolata. Esetünkben egy olyan pipeline-t hozunk létre, amely először polinomiális jellemzőket ad a modellhez, majd elvégzi a regressziót: ```python from sklearn.preprocessing import PolynomialFeatures from sklearn.pipeline import make_pipeline pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression()) pipeline.fit(X_train,y_train) ``` A `PolynomialFeatures(2)` használata azt jelenti, hogy a bemeneti adatokból minden másodfokú polinomot beillesztünk. Esetünkben ez csak a `DayOfYear`²-t jelenti, de ha két bemeneti változónk van, X és Y, akkor ez hozzáadja X²-t, XY-t és Y²-t. Magasabb fokú polinomokat is használhatunk, ha szeretnénk. A pipeline-t ugyanúgy használhatjuk, mint az eredeti `LinearRegression` objektumot, azaz `fit`-elhetjük a pipeline-t, majd a `predict` segítségével megkaphatjuk az előrejelzési eredményeket. Íme a grafikon, amely a tesztadatokat és az approximációs görbét mutatja: A polinomiális regresszió használatával kissé alacsonyabb MSE-t és magasabb determinizációs együtthatót érhetünk el, de nem jelentősen. Figyelembe kell vennünk más jellemzőket is! > Láthatod, hogy a tökök legalacsonyabb árai valahol Halloween környékén figyelhetők meg. Hogyan magyaráznád ezt? 🎃 Gratulálok, most létrehoztál egy modellt, amely segíthet a pite tökök árának előrejelzésében. Valószínűleg ugyanezt az eljárást megismételheted az összes tökfajtára, de ez elég fárasztó lenne. Most tanuljuk meg, hogyan vegyük figyelembe a tökfajtákat a modellünkben! ## Kategorikus jellemzők Az ideális világban szeretnénk képesek lenni előre jelezni az árakat különböző tökfajtákra ugyanazzal a modellel. Azonban a `Variety` oszlop kissé eltér az olyan oszlopoktól, mint a `Month`, mert nem numerikus értékeket tartalmaz. Az ilyen oszlopokat **kategorikus** oszlopoknak nevezzük. [](https://youtu.be/DYGliioIAE0 "ML kezdőknek - Kategorikus jellemzők előrejelzése lineáris regresszióval") > 🎥 Kattints a fenti képre egy rövid videós áttekintésért a kategorikus jellemzők használatáról. Itt láthatod, hogyan függ az átlagár a fajtától: Ahhoz, hogy figyelembe vegyük a fajtát, először numerikus formára kell átalakítanunk, vagyis **kódolnunk** kell. Többféle módon tehetjük ezt meg: * Az egyszerű **numerikus kódolás** egy táblázatot készít a különböző fajtákról, majd a fajta nevét egy indexszel helyettesíti a táblázatban. Ez nem a legjobb ötlet a lineáris regresszióhoz, mert a lineáris regresszió az index tényleges numerikus értékét veszi figyelembe, és hozzáadja az eredményhez, megszorozva egy együtthatóval. Esetünkben az indexszám és az ár közötti kapcsolat egyértelműen nem lineáris, még akkor sem, ha biztosítjuk, hogy az indexek valamilyen specifikus sorrendben legyenek. * A **one-hot kódolás** a `Variety` oszlopot 4 különböző oszlopra cseréli, egyet minden fajtához. Minden oszlop `1`-et tartalmaz, ha az adott sor egy adott fajtához tartozik, és `0`-t, ha nem. Ez azt jelenti, hogy a lineáris regresszióban négy együttható lesz, egy-egy minden tökfajtához, amely felelős az adott fajta "kezdő árának" (vagy inkább "további árának"). Az alábbi kód megmutatja, hogyan kódolhatjuk one-hot módszerrel a fajtát: ```python pd.get_dummies(new_pumpkins['Variety']) ``` ID | FAIRYTALE | MINIATURE | MIXED HEIRLOOM VARIETIES | PIE TYPE ----|-----------|-----------|--------------------------|---------- 70 | 0 | 0 | 0 | 1 71 | 0 | 0 | 0 | 1 ... | ... | ... | ... | ... 1738 | 0 | 1 | 0 | 0 1739 | 0 | 1 | 0 | 0 1740 | 0 | 1 | 0 | 0 1741 | 0 | 1 | 0 | 0 1742 | 0 | 1 | 0 | 0 Ahhoz, hogy lineáris regressziót tanítsunk one-hot kódolt fajta bemeneti adatokkal, csak helyesen kell inicializálnunk az `X` és `y` adatokat: ```python X = pd.get_dummies(new_pumpkins['Variety']) y = new_pumpkins['Price'] ``` A többi kód ugyanaz, mint amit korábban használtunk a lineáris regresszió tanításához. Ha kipróbálod, látni fogod, hogy az átlagos négyzetes hiba körülbelül ugyanaz, de sokkal magasabb determinizációs együtthatót kapunk (~77%). Ahhoz, hogy még pontosabb előrejelzéseket kapjunk, több kategorikus jellemzőt is figyelembe vehetünk, valamint numerikus jellemzőket, mint például a `Month` vagy a `DayOfYear`. Egy nagy jellemzőtömb létrehozásához használhatjuk a `join`-t: ```python X = pd.get_dummies(new_pumpkins['Variety']) \ .join(new_pumpkins['Month']) \ .join(pd.get_dummies(new_pumpkins['City'])) \ .join(pd.get_dummies(new_pumpkins['Package'])) y = new_pumpkins['Price'] ``` Itt figyelembe vesszük a `City` és a `Package` típusát is, ami 2.84-es MSE-t (10%) és 0.94-es determinizációs együtthatót eredményez! ## Mindent összefoglalva A legjobb modell létrehozásához használhatjuk a fenti példából származó kombinált (one-hot kódolt kategorikus + numerikus) adatokat polinomiális regresszióval együtt. Íme a teljes kód a kényelmed érdekében: ```python # set up training data X = pd.get_dummies(new_pumpkins['Variety']) \ .join(new_pumpkins['Month']) \ .join(pd.get_dummies(new_pumpkins['City'])) \ .join(pd.get_dummies(new_pumpkins['Package'])) y = new_pumpkins['Price'] # make train-test split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) # setup and train the pipeline pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression()) pipeline.fit(X_train,y_train) # predict results for test data pred = pipeline.predict(X_test) # calculate MSE and determination mse = np.sqrt(mean_squared_error(y_test,pred)) print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)') score = pipeline.score(X_train,y_train) print('Model determination: ', score) ``` Ez közel 97%-os determinizációs együtthatót és MSE=2.23 (~8%-os előrejelzési hiba) eredményez. | Modell | MSE | Determinizáció | |-------|-----|---------------| | `DayOfYear` Lineáris | 2.77 (17.2%) | 0.07 | | `DayOfYear` Polinomiális | 2.73 (17.0%) | 0.08 | | `Variety` Lineáris | 5.24 (19.7%) | 0.77 | | Minden jellemző Lineáris | 2.84 (10.5%) | 0.94 | | Minden jellemző Polinomiális | 2.23 (8.25%) | 0.97 | 🏆 Szép munka! Egyetlen leckében négy regressziós modellt hoztál létre, és a modell minőségét 97%-ra javítottad. A regresszióról szóló utolsó részben a logisztikus regresszióval fogsz megismerkedni, amely kategóriák meghatározására szolgál. --- ## 🚀Kihívás Tesztelj több különböző változót ebben a notebookban, hogy lásd, hogyan függ össze a korreláció a modell pontosságával. ## [Utólagos kvíz](https://ff-quizzes.netlify.app/en/ml/) ## Áttekintés és önálló tanulás Ebben a leckében a lineáris regresszióról tanultunk. Vannak más fontos regressziós technikák is. Olvass a Stepwise, Ridge, Lasso és Elasticnet technikákról. Egy jó kurzus, amelyet érdemes tanulmányozni, a [Stanford Statistical Learning kurzus](https://online.stanford.edu/courses/sohs-ystatslearning-statistical-learning). ## Feladat [Építs egy modellt](assignment.md) --- **Felelősség kizárása**: Ez a dokumentum az AI fordítási szolgáltatás [Co-op Translator](https://github.com/Azure/co-op-translator) segítségével lett lefordítva. Bár törekszünk a pontosságra, kérjük, vegye figyelembe, hogy az automatikus fordítások hibákat vagy pontatlanságokat tartalmazhatnak. Az eredeti dokumentum az eredeti nyelvén tekintendő hiteles forrásnak. Kritikus információk esetén javasolt professzionális emberi fordítást igénybe venni. Nem vállalunk felelősséget semmilyen félreértésért vagy téves értelmezésért, amely a fordítás használatából eredhet.