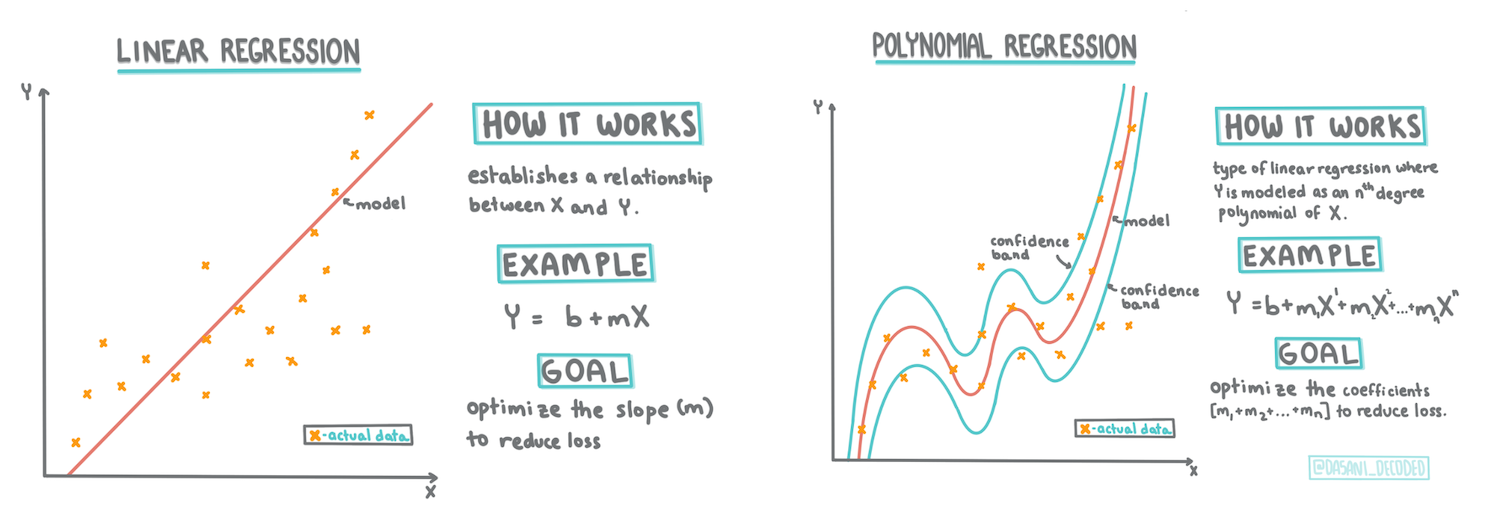
# Construir un modelo de regresión usando Scikit-learn: cuatro formas de regresión  > Infografía por [Dasani Madipalli](https://twitter.com/dasani_decoded) ## [Cuestionario previo a la lección](https://ff-quizzes.netlify.app/en/ml/) > ### [¡Esta lección está disponible en R!](../../../../2-Regression/3-Linear/solution/R/lesson_3.html) ### Introducción Hasta ahora has explorado qué es la regresión con datos de muestra obtenidos del conjunto de datos de precios de calabazas que utilizaremos a lo largo de esta lección. También lo has visualizado utilizando Matplotlib. Ahora estás listo para profundizar más en la regresión para ML. Mientras que la visualización te permite comprender los datos, el verdadero poder del aprendizaje automático proviene del _entrenamiento de modelos_. Los modelos se entrenan con datos históricos para capturar automáticamente las dependencias de los datos, y te permiten predecir resultados para nuevos datos que el modelo no ha visto antes. En esta lección, aprenderás más sobre dos tipos de regresión: _regresión lineal básica_ y _regresión polinómica_, junto con algunas de las matemáticas subyacentes a estas técnicas. Estos modelos nos permitirán predecir los precios de las calabazas dependiendo de diferentes datos de entrada. [](https://youtu.be/CRxFT8oTDMg "ML para principiantes - Entendiendo la regresión lineal") > 🎥 Haz clic en la imagen de arriba para un breve video sobre la regresión lineal. > A lo largo de este plan de estudios, asumimos un conocimiento mínimo de matemáticas y buscamos hacerlo accesible para estudiantes provenientes de otros campos, así que presta atención a las notas, 🧮 llamados, diagramas y otras herramientas de aprendizaje para facilitar la comprensión. ### Prerrequisitos A estas alturas deberías estar familiarizado con la estructura de los datos de calabazas que estamos examinando. Puedes encontrarlos precargados y preprocesados en el archivo _notebook.ipynb_ de esta lección. En el archivo, el precio de las calabazas se muestra por bushel en un nuevo marco de datos. Asegúrate de poder ejecutar estos notebooks en kernels en Visual Studio Code. ### Preparación Como recordatorio, estás cargando estos datos para hacer preguntas sobre ellos. - ¿Cuándo es el mejor momento para comprar calabazas? - ¿Qué precio puedo esperar por un paquete de calabazas miniatura? - ¿Debería comprarlas en cestas de medio bushel o en cajas de 1 1/9 bushel? Sigamos investigando estos datos. En la lección anterior, creaste un marco de datos de Pandas y lo llenaste con parte del conjunto de datos original, estandarizando los precios por bushel. Sin embargo, al hacer eso, solo pudiste recopilar alrededor de 400 puntos de datos y solo para los meses de otoño. Echa un vistazo a los datos que precargamos en el notebook que acompaña esta lección. Los datos están precargados y se ha trazado un gráfico de dispersión inicial para mostrar los datos por mes. Tal vez podamos obtener un poco más de detalle sobre la naturaleza de los datos limpiándolos más. ## Una línea de regresión lineal Como aprendiste en la Lección 1, el objetivo de un ejercicio de regresión lineal es poder trazar una línea para: - **Mostrar relaciones entre variables**. Mostrar la relación entre las variables. - **Hacer predicciones**. Hacer predicciones precisas sobre dónde caería un nuevo punto de datos en relación con esa línea. Es típico de la **Regresión de Mínimos Cuadrados** trazar este tipo de línea. El término 'mínimos cuadrados' significa que todos los puntos de datos que rodean la línea de regresión se elevan al cuadrado y luego se suman. Idealmente, esa suma final es lo más pequeña posible, porque queremos un número bajo de errores, o `mínimos cuadrados`. Hacemos esto porque queremos modelar una línea que tenga la menor distancia acumulada de todos nuestros puntos de datos. También elevamos los términos al cuadrado antes de sumarlos porque nos interesa su magnitud más que su dirección. 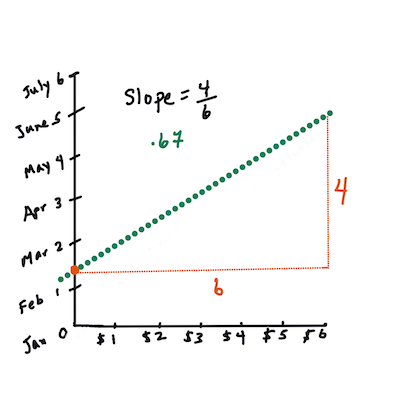> **🧮 Muéstrame las matemáticas** > > Esta línea, llamada _línea de mejor ajuste_, puede expresarse mediante [una ecuación](https://en.wikipedia.org/wiki/Simple_linear_regression): > > ``` > Y = a + bX > ``` > > `X` es la 'variable explicativa'. `Y` es la 'variable dependiente'. La pendiente de la línea es `b` y `a` es la intersección con el eje Y, que se refiere al valor de `Y` cuando `X = 0`. > > > > Primero, calcula la pendiente `b`. 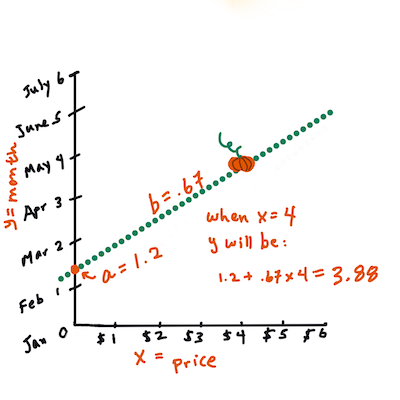Infografía por [Jen Looper](https://twitter.com/jenlooper) > > En otras palabras, y refiriéndonos a la pregunta original de los datos de calabazas: "predecir el precio de una calabaza por bushel según el mes", `X` se referiría al precio y `Y` se referiría al mes de venta. > > > > Calcula el valor de Y. Si estás pagando alrededor de $4, ¡debe ser abril! Infografía por [Jen Looper](https://twitter.com/jenlooper) > > Las matemáticas que calculan la línea deben demostrar la pendiente de la línea, que también depende de la intersección, o dónde se sitúa `Y` cuando `X = 0`. > > Puedes observar el método de cálculo para estos valores en el sitio web [Math is Fun](https://www.mathsisfun.com/data/least-squares-regression.html). También visita [este calculador de mínimos cuadrados](https://www.mathsisfun.com/data/least-squares-calculator.html) para ver cómo los valores de los números afectan la línea. ## Correlación Otro término que debes entender es el **Coeficiente de Correlación** entre las variables X e Y dadas. Usando un gráfico de dispersión, puedes visualizar rápidamente este coeficiente. Un gráfico con puntos de datos dispersos en una línea ordenada tiene alta correlación, pero un gráfico con puntos de datos dispersos por todas partes entre X e Y tiene baja correlación. Un buen modelo de regresión lineal será aquel que tenga un Coeficiente de Correlación alto (más cercano a 1 que a 0) utilizando el método de Regresión de Mínimos Cuadrados con una línea de regresión. ✅ Ejecuta el notebook que acompaña esta lección y observa el gráfico de dispersión de Mes a Precio. Según tu interpretación visual del gráfico de dispersión, ¿parece que los datos que asocian Mes con Precio para las ventas de calabazas tienen alta o baja correlación? ¿Cambia eso si usas una medida más detallada en lugar de `Mes`, por ejemplo, *día del año* (es decir, el número de días desde el inicio del año)? En el código a continuación, asumiremos que hemos limpiado los datos y obtenido un marco de datos llamado `new_pumpkins`, similar al siguiente: ID | Mes | DíaDelAño | Variedad | Ciudad | Paquete | Precio Bajo | Precio Alto | Precio ---|-----|-----------|----------|--------|---------|-------------|-------------|------- 70 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 15.0 | 15.0 | 13.636364 71 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 18.0 | 18.0 | 16.363636 72 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 18.0 | 18.0 | 16.363636 73 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 17.0 | 17.0 | 15.454545 74 | 10 | 281 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 15.0 | 15.0 | 13.636364 > El código para limpiar los datos está disponible en [`notebook.ipynb`](../../../../2-Regression/3-Linear/notebook.ipynb). Hemos realizado los mismos pasos de limpieza que en la lección anterior y hemos calculado la columna `DíaDelAño` utilizando la siguiente expresión: ```python day_of_year = pd.to_datetime(pumpkins['Date']).apply(lambda dt: (dt-datetime(dt.year,1,1)).days) ``` Ahora que tienes una comprensión de las matemáticas detrás de la regresión lineal, vamos a crear un modelo de Regresión para ver si podemos predecir qué paquete de calabazas tendrá los mejores precios. Alguien que compre calabazas para un huerto de calabazas festivo podría querer esta información para optimizar sus compras de paquetes de calabazas para el huerto. ## Buscando correlación [](https://youtu.be/uoRq-lW2eQo "ML para principiantes - Buscando correlación: La clave para la regresión lineal") > 🎥 Haz clic en la imagen de arriba para un breve video sobre la correlación. De la lección anterior probablemente hayas visto que el precio promedio para diferentes meses se ve así: Esto sugiere que debería haber alguna correlación, y podemos intentar entrenar un modelo de regresión lineal para predecir la relación entre `Mes` y `Precio`, o entre `DíaDelAño` y `Precio`. Aquí está el gráfico de dispersión que muestra esta última relación: Veamos si hay una correlación usando la función `corr`: ```python print(new_pumpkins['Month'].corr(new_pumpkins['Price'])) print(new_pumpkins['DayOfYear'].corr(new_pumpkins['Price'])) ``` Parece que la correlación es bastante pequeña, -0.15 por `Mes` y -0.17 por `DíaDelAño`, pero podría haber otra relación importante. Parece que hay diferentes grupos de precios que corresponden a diferentes variedades de calabazas. Para confirmar esta hipótesis, tracemos cada categoría de calabaza usando un color diferente. Al pasar un parámetro `ax` a la función de trazado de dispersión podemos trazar todos los puntos en el mismo gráfico: ```python ax=None colors = ['red','blue','green','yellow'] for i,var in enumerate(new_pumpkins['Variety'].unique()): df = new_pumpkins[new_pumpkins['Variety']==var] ax = df.plot.scatter('DayOfYear','Price',ax=ax,c=colors[i],label=var) ``` Nuestra investigación sugiere que la variedad tiene más efecto en el precio general que la fecha de venta real. Podemos ver esto con un gráfico de barras: ```python new_pumpkins.groupby('Variety')['Price'].mean().plot(kind='bar') ``` Centrémonos por el momento solo en una variedad de calabaza, el 'tipo pie', y veamos qué efecto tiene la fecha en el precio: ```python pie_pumpkins = new_pumpkins[new_pumpkins['Variety']=='PIE TYPE'] pie_pumpkins.plot.scatter('DayOfYear','Price') ``` Si ahora calculamos la correlación entre `Precio` y `DíaDelAño` usando la función `corr`, obtendremos algo como `-0.27`, lo que significa que tiene sentido entrenar un modelo predictivo. > Antes de entrenar un modelo de regresión lineal, es importante asegurarse de que nuestros datos estén limpios. La regresión lineal no funciona bien con valores faltantes, por lo que tiene sentido deshacerse de todas las celdas vacías: ```python pie_pumpkins.dropna(inplace=True) pie_pumpkins.info() ``` Otra opción sería llenar esos valores vacíos con valores promedio de la columna correspondiente. ## Regresión Lineal Simple [](https://youtu.be/e4c_UP2fSjg "ML para principiantes - Regresión Lineal y Polinómica usando Scikit-learn") > 🎥 Haz clic en la imagen de arriba para un breve video sobre regresión lineal y polinómica. Para entrenar nuestro modelo de Regresión Lineal, utilizaremos la biblioteca **Scikit-learn**. ```python from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error from sklearn.model_selection import train_test_split ``` Comenzamos separando los valores de entrada (características) y la salida esperada (etiqueta) en matrices numpy separadas: ```python X = pie_pumpkins['DayOfYear'].to_numpy().reshape(-1,1) y = pie_pumpkins['Price'] ``` > Nota que tuvimos que realizar un `reshape` en los datos de entrada para que el paquete de Regresión Lineal los entienda correctamente. La Regresión Lineal espera una matriz 2D como entrada, donde cada fila de la matriz corresponde a un vector de características de entrada. En nuestro caso, dado que solo tenemos una entrada, necesitamos una matriz con forma N×1, donde N es el tamaño del conjunto de datos. Luego, necesitamos dividir los datos en conjuntos de entrenamiento y prueba, para que podamos validar nuestro modelo después del entrenamiento: ```python X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) ``` Finalmente, entrenar el modelo de Regresión Lineal real toma solo dos líneas de código. Definimos el objeto `LinearRegression` y lo ajustamos a nuestros datos usando el método `fit`: ```python lin_reg = LinearRegression() lin_reg.fit(X_train,y_train) ``` El objeto `LinearRegression` después de ajustarse contiene todos los coeficientes de la regresión, que se pueden acceder usando la propiedad `.coef_`. En nuestro caso, solo hay un coeficiente, que debería estar alrededor de `-0.017`. Esto significa que los precios parecen bajar un poco con el tiempo, pero no demasiado, alrededor de 2 centavos por día. También podemos acceder al punto de intersección de la regresión con el eje Y usando `lin_reg.intercept_`, que estará alrededor de `21` en nuestro caso, indicando el precio al comienzo del año. Para ver qué tan preciso es nuestro modelo, podemos predecir precios en un conjunto de datos de prueba y luego medir qué tan cerca están nuestras predicciones de los valores esperados. Esto se puede hacer usando la métrica de error cuadrático medio (MSE), que es el promedio de todas las diferencias al cuadrado entre el valor esperado y el predicho. ```python pred = lin_reg.predict(X_test) mse = np.sqrt(mean_squared_error(y_test,pred)) print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)') ``` Nuestro error parece estar en torno a 2 puntos, lo que equivale a ~17%. No es muy bueno. Otro indicador de la calidad del modelo es el **coeficiente de determinación**, que se puede obtener de la siguiente manera: ```python score = lin_reg.score(X_train,y_train) print('Model determination: ', score) ``` Si el valor es 0, significa que el modelo no toma en cuenta los datos de entrada y actúa como el *peor predictor lineal*, que simplemente es el valor promedio del resultado. Un valor de 1 significa que podemos predecir perfectamente todos los resultados esperados. En nuestro caso, el coeficiente está alrededor de 0.06, lo cual es bastante bajo. También podemos graficar los datos de prueba junto con la línea de regresión para ver mejor cómo funciona la regresión en nuestro caso: ```python plt.scatter(X_test,y_test) plt.plot(X_test,pred) ``` ## Regresión Polinómica Otro tipo de Regresión Lineal es la Regresión Polinómica. Aunque a veces existe una relación lineal entre las variables - cuanto mayor es el volumen de la calabaza, mayor es el precio - en otras ocasiones estas relaciones no pueden representarse como un plano o una línea recta. ✅ Aquí hay [algunos ejemplos](https://online.stat.psu.edu/stat501/lesson/9/9.8) de datos que podrían usar Regresión Polinómica. Observa nuevamente la relación entre Fecha y Precio. ¿Este diagrama de dispersión parece que debería analizarse necesariamente con una línea recta? ¿No pueden fluctuar los precios? En este caso, puedes intentar con regresión polinómica. ✅ Los polinomios son expresiones matemáticas que pueden consistir en una o más variables y coeficientes. La regresión polinómica crea una línea curva para ajustar mejor los datos no lineales. En nuestro caso, si incluimos una variable `DayOfYear` al cuadrado en los datos de entrada, deberíamos poder ajustar nuestros datos con una curva parabólica, que tendrá un mínimo en cierto punto del año. Scikit-learn incluye una útil [API de pipeline](https://scikit-learn.org/stable/modules/generated/sklearn.pipeline.make_pipeline.html?highlight=pipeline#sklearn.pipeline.make_pipeline) para combinar diferentes pasos de procesamiento de datos. Un **pipeline** es una cadena de **estimadores**. En nuestro caso, crearemos un pipeline que primero agrega características polinómicas a nuestro modelo y luego entrena la regresión: ```python from sklearn.preprocessing import PolynomialFeatures from sklearn.pipeline import make_pipeline pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression()) pipeline.fit(X_train,y_train) ``` Usar `PolynomialFeatures(2)` significa que incluiremos todos los polinomios de segundo grado de los datos de entrada. En nuestro caso, esto simplemente significará `DayOfYear`², pero dado dos variables de entrada X e Y, esto agregará X², XY y Y². También podemos usar polinomios de mayor grado si lo deseamos. Los pipelines pueden usarse de la misma manera que el objeto original `LinearRegression`, es decir, podemos usar `fit` en el pipeline y luego usar `predict` para obtener los resultados de predicción. Aquí está el gráfico que muestra los datos de prueba y la curva de aproximación: Usando Regresión Polinómica, podemos obtener un MSE ligeramente más bajo y un coeficiente de determinación más alto, pero no significativamente. ¡Necesitamos tomar en cuenta otras características! > Puedes observar que los precios mínimos de las calabazas se registran en algún momento cerca de Halloween. ¿Cómo puedes explicar esto? 🎃 ¡Felicidades! Acabas de crear un modelo que puede ayudar a predecir el precio de las calabazas para pastel. Probablemente podrías repetir el mismo procedimiento para todos los tipos de calabazas, pero eso sería tedioso. ¡Ahora aprendamos cómo tomar en cuenta la variedad de calabazas en nuestro modelo! ## Características Categóricas En un mundo ideal, queremos poder predecir precios para diferentes variedades de calabazas usando el mismo modelo. Sin embargo, la columna `Variety` es algo diferente de columnas como `Month`, porque contiene valores no numéricos. Estas columnas se llaman **categóricas**. [](https://youtu.be/DYGliioIAE0 "ML para principiantes - Predicciones con características categóricas usando Regresión Lineal") > 🎥 Haz clic en la imagen de arriba para ver un breve video sobre el uso de características categóricas. Aquí puedes ver cómo el precio promedio depende de la variedad: Para tomar en cuenta la variedad, primero necesitamos convertirla a forma numérica, o **codificarla**. Hay varias maneras de hacerlo: * La **codificación numérica simple** construirá una tabla de diferentes variedades y luego reemplazará el nombre de la variedad por un índice en esa tabla. Esta no es la mejor idea para la regresión lineal, porque la regresión lineal toma el valor numérico real del índice y lo agrega al resultado, multiplicándolo por algún coeficiente. En nuestro caso, la relación entre el número de índice y el precio claramente no es lineal, incluso si nos aseguramos de que los índices estén ordenados de alguna manera específica. * La **codificación one-hot** reemplazará la columna `Variety` por 4 columnas diferentes, una para cada variedad. Cada columna contendrá `1` si la fila correspondiente es de una variedad dada, y `0` en caso contrario. Esto significa que habrá cuatro coeficientes en la regresión lineal, uno para cada variedad de calabaza, responsables del "precio inicial" (o más bien "precio adicional") para esa variedad en particular. El siguiente código muestra cómo podemos codificar una variedad usando one-hot: ```python pd.get_dummies(new_pumpkins['Variety']) ``` ID | FAIRYTALE | MINIATURE | MIXED HEIRLOOM VARIETIES | PIE TYPE ----|-----------|-----------|--------------------------|---------- 70 | 0 | 0 | 0 | 1 71 | 0 | 0 | 0 | 1 ... | ... | ... | ... | ... 1738 | 0 | 1 | 0 | 0 1739 | 0 | 1 | 0 | 0 1740 | 0 | 1 | 0 | 0 1741 | 0 | 1 | 0 | 0 1742 | 0 | 1 | 0 | 0 Para entrenar la regresión lineal usando la variedad codificada como one-hot en los datos de entrada, solo necesitamos inicializar correctamente los datos `X` y `y`: ```python X = pd.get_dummies(new_pumpkins['Variety']) y = new_pumpkins['Price'] ``` El resto del código es el mismo que usamos anteriormente para entrenar la Regresión Lineal. Si lo pruebas, verás que el error cuadrático medio es aproximadamente el mismo, pero obtenemos un coeficiente de determinación mucho más alto (~77%). Para obtener predicciones aún más precisas, podemos tomar en cuenta más características categóricas, así como características numéricas, como `Month` o `DayOfYear`. Para obtener un gran conjunto de características, podemos usar `join`: ```python X = pd.get_dummies(new_pumpkins['Variety']) \ .join(new_pumpkins['Month']) \ .join(pd.get_dummies(new_pumpkins['City'])) \ .join(pd.get_dummies(new_pumpkins['Package'])) y = new_pumpkins['Price'] ``` Aquí también tomamos en cuenta `City` y el tipo de `Package`, lo que nos da un MSE de 2.84 (10%) y un coeficiente de determinación de 0.94. ## Juntándolo todo Para crear el mejor modelo, podemos usar datos combinados (categóricos codificados como one-hot + numéricos) del ejemplo anterior junto con Regresión Polinómica. Aquí está el código completo para tu conveniencia: ```python # set up training data X = pd.get_dummies(new_pumpkins['Variety']) \ .join(new_pumpkins['Month']) \ .join(pd.get_dummies(new_pumpkins['City'])) \ .join(pd.get_dummies(new_pumpkins['Package'])) y = new_pumpkins['Price'] # make train-test split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) # setup and train the pipeline pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression()) pipeline.fit(X_train,y_train) # predict results for test data pred = pipeline.predict(X_test) # calculate MSE and determination mse = np.sqrt(mean_squared_error(y_test,pred)) print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)') score = pipeline.score(X_train,y_train) print('Model determination: ', score) ``` Esto debería darnos el mejor coeficiente de determinación de casi 97% y un MSE=2.23 (~8% de error de predicción). | Modelo | MSE | Determinación | |--------|-----|---------------| | `DayOfYear` Lineal | 2.77 (17.2%) | 0.07 | | `DayOfYear` Polinómico | 2.73 (17.0%) | 0.08 | | `Variety` Lineal | 5.24 (19.7%) | 0.77 | | Todas las características Lineal | 2.84 (10.5%) | 0.94 | | Todas las características Polinómico | 2.23 (8.25%) | 0.97 | 🏆 ¡Bien hecho! Creaste cuatro modelos de Regresión en una sola lección y mejoraste la calidad del modelo al 97%. En la sección final sobre Regresión, aprenderás sobre Regresión Logística para determinar categorías. --- ## 🚀Desafío Prueba varias variables diferentes en este notebook para ver cómo la correlación corresponde a la precisión del modelo. ## [Cuestionario posterior a la lección](https://ff-quizzes.netlify.app/en/ml/) ## Revisión y Autoestudio En esta lección aprendimos sobre Regresión Lineal. Hay otros tipos importantes de Regresión. Lee sobre las técnicas Stepwise, Ridge, Lasso y Elasticnet. Un buen curso para estudiar y aprender más es el [curso de Stanford sobre Aprendizaje Estadístico](https://online.stanford.edu/courses/sohs-ystatslearning-statistical-learning). ## Tarea [Construye un Modelo](assignment.md) --- **Descargo de responsabilidad**: Este documento ha sido traducido utilizando el servicio de traducción automática [Co-op Translator](https://github.com/Azure/co-op-translator). Si bien nos esforzamos por lograr precisión, tenga en cuenta que las traducciones automáticas pueden contener errores o imprecisiones. El documento original en su idioma nativo debe considerarse como la fuente autorizada. Para información crítica, se recomienda una traducción profesional realizada por humanos. No nos hacemos responsables de malentendidos o interpretaciones erróneas que puedan surgir del uso de esta traducción.