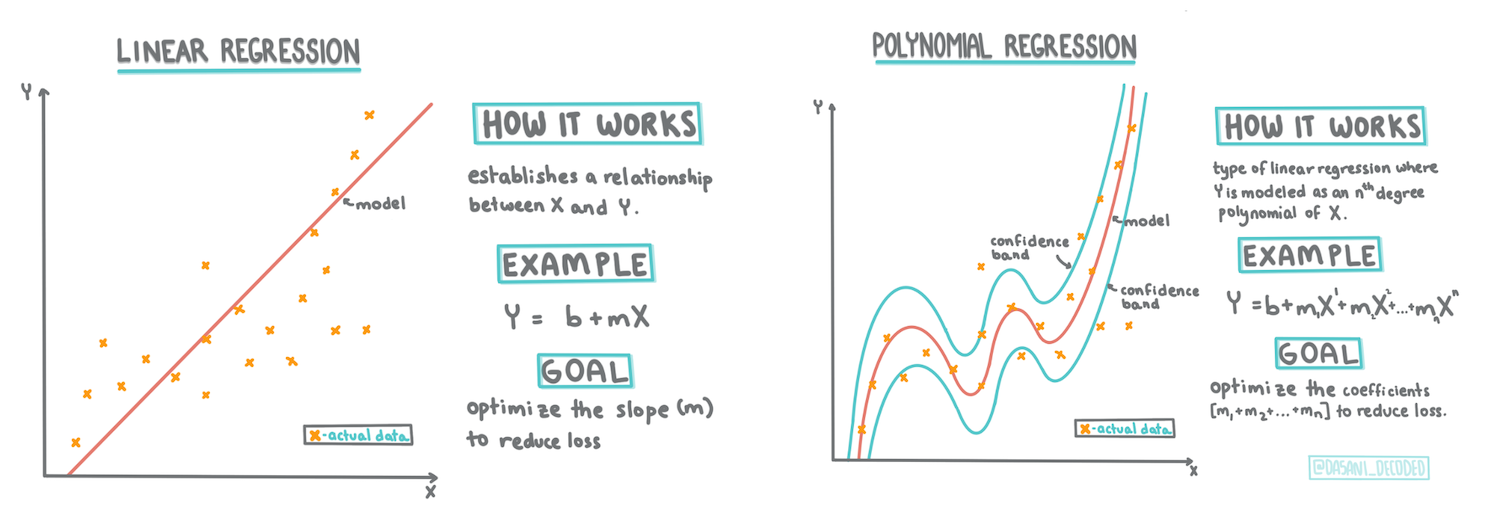
# بناء نموذج انحدار باستخدام Scikit-learn: الانحدار بأربع طرق  > مخطط معلوماتي بواسطة [Dasani Madipalli](https://twitter.com/dasani_decoded) ## [اختبار ما قبل المحاضرة](https://ff-quizzes.netlify.app/en/ml/) > ### [هذه الدرس متوفر بلغة R!](../../../../2-Regression/3-Linear/solution/R/lesson_3.html) ### المقدمة حتى الآن، قمت باستكشاف مفهوم الانحدار باستخدام بيانات عينة مأخوذة من مجموعة بيانات تسعير القرع التي سنستخدمها طوال هذا الدرس. كما قمت بتصورها باستخدام مكتبة Matplotlib. الآن أنت جاهز للتعمق أكثر في الانحدار في تعلم الآلة. بينما يسمح التصور بفهم البيانات، فإن القوة الحقيقية لتعلم الآلة تأتي من _تدريب النماذج_. يتم تدريب النماذج على البيانات التاريخية لالتقاط العلاقات بين البيانات تلقائيًا، وتتيح لك التنبؤ بالنتائج للبيانات الجديدة التي لم يرها النموذج من قبل. في هذا الدرس، ستتعلم المزيد عن نوعين من الانحدار: _الانحدار الخطي الأساسي_ و _الانحدار متعدد الحدود_، إلى جانب بعض الرياضيات الأساسية لهذه التقنيات. ستتيح لنا هذه النماذج التنبؤ بأسعار القرع بناءً على بيانات الإدخال المختلفة. [](https://youtu.be/CRxFT8oTDMg "تعلّم الآلة للمبتدئين - فهم الانحدار الخطي") > 🎥 انقر على الصورة أعلاه لمشاهدة فيديو قصير عن الانحدار الخطي. > خلال هذه المنهجية، نفترض معرفة بسيطة بالرياضيات، ونسعى لجعلها سهلة الوصول للطلاب القادمين من مجالات أخرى، لذا ابحث عن الملاحظات، 🧮 التنبيهات، الرسوم البيانية، وأدوات التعلم الأخرى لتسهيل الفهم. ### المتطلبات الأساسية يجب أن تكون الآن على دراية ببنية بيانات القرع التي نقوم بفحصها. يمكنك العثور عليها محملة مسبقًا ومُنظفة مسبقًا في ملف _notebook.ipynb_ الخاص بهذا الدرس. في الملف، يتم عرض سعر القرع لكل بوشل في إطار بيانات جديد. تأكد من أنك تستطيع تشغيل هذه الدفاتر في النواة الخاصة بـ Visual Studio Code. ### التحضير كتذكير، أنت تقوم بتحميل هذه البيانات لطرح أسئلة عليها. - متى يكون أفضل وقت لشراء القرع؟ - ما السعر المتوقع لصندوق من القرع الصغير؟ - هل يجب أن أشتريه في سلال نصف بوشل أو في صناديق بوشل 1 1/9؟ دعونا نستمر في استكشاف هذه البيانات. في الدرس السابق، قمت بإنشاء إطار بيانات باستخدام Pandas وملأته بجزء من مجموعة البيانات الأصلية، موحدًا التسعير حسب البوشل. ومع ذلك، من خلال القيام بذلك، تمكنت فقط من جمع حوالي 400 نقطة بيانات وفقط للأشهر الخريفية. ألقِ نظرة على البيانات التي قمنا بتحميلها مسبقًا في دفتر الملاحظات المرافق لهذا الدرس. البيانات محملة مسبقًا وتم رسم مخطط مبعثر أولي لإظهار بيانات الأشهر. ربما يمكننا الحصول على مزيد من التفاصيل حول طبيعة البيانات من خلال تنظيفها أكثر. ## خط الانحدار الخطي كما تعلمت في الدرس الأول، الهدف من تمرين الانحدار الخطي هو القدرة على رسم خط لـ: - **إظهار العلاقات بين المتغيرات**. إظهار العلاقة بين المتغيرات - **إجراء التنبؤات**. إجراء تنبؤات دقيقة حول مكان وقوع نقطة بيانات جديدة بالنسبة لذلك الخط. من المعتاد استخدام **انحدار المربعات الصغرى** لرسم هذا النوع من الخطوط. مصطلح "المربعات الصغرى" يعني أن جميع نقاط البيانات المحيطة بخط الانحدار يتم تربيعها ثم جمعها. من الناحية المثالية، يكون المجموع النهائي صغيرًا قدر الإمكان، لأننا نريد عددًا منخفضًا من الأخطاء، أو `المربعات الصغرى`. نقوم بذلك لأننا نريد نمذجة خط يحتوي على أقل مسافة تراكمية من جميع نقاط البيانات لدينا. كما نقوم بتربيع المصطلحات قبل جمعها لأننا نهتم بحجمها بدلاً من اتجاهها. 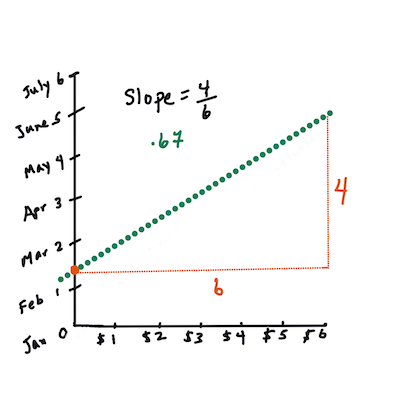> **🧮 أرني الرياضيات** > > يمكن التعبير عن هذا الخط، المسمى _خط أفضل تطابق_، بواسطة [معادلة](https://en.wikipedia.org/wiki/Simple_linear_regression): > > ``` > Y = a + bX > ``` > > `X` هو "المتغير التوضيحي". `Y` هو "المتغير التابع". ميل الخط هو `b` و `a` هو نقطة تقاطع المحور Y، والتي تشير إلى قيمة `Y` عندما يكون `X = 0`. > > > > أولاً، احسب الميل `b`. مخطط معلوماتي بواسطة [Jen Looper](https://twitter.com/jenlooper) > > بعبارة أخرى، وبالإشارة إلى السؤال الأصلي لبيانات القرع: "توقع سعر القرع لكل بوشل حسب الشهر"، سيكون `X` يشير إلى السعر و `Y` يشير إلى شهر البيع. 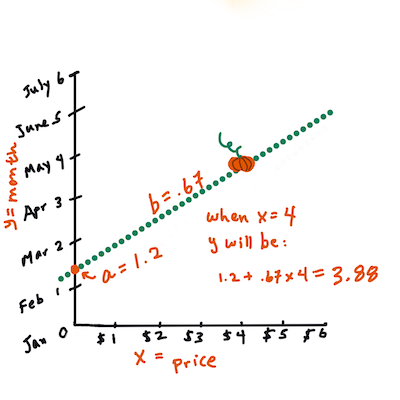> > > > احسب قيمة Y. إذا كنت تدفع حوالي 4 دولارات، فلا بد أن يكون أبريل! مخطط معلوماتي بواسطة [Jen Looper](https://twitter.com/jenlooper) > > يجب أن تُظهر الرياضيات التي تحسب الخط ميل الخط، والذي يعتمد أيضًا على نقطة التقاطع، أو مكان وجود `Y` عندما يكون `X = 0`. > > يمكنك مشاهدة طريقة الحساب لهذه القيم على موقع [Math is Fun](https://www.mathsisfun.com/data/least-squares-regression.html). كما يمكنك زيارة [آلة حاسبة المربعات الصغرى](https://www.mathsisfun.com/data/least-squares-calculator.html) لمشاهدة كيف تؤثر قيم الأرقام على الخط. ## الارتباط مصطلح آخر يجب فهمه هو **معامل الارتباط** بين المتغيرين X و Y المعطىين. باستخدام مخطط مبعثر، يمكنك بسرعة تصور هذا المعامل. مخطط يحتوي على نقاط بيانات متناثرة في خط مرتب لديه ارتباط عالي، ولكن مخطط يحتوي على نقاط بيانات متناثرة في كل مكان بين X و Y لديه ارتباط منخفض. نموذج الانحدار الخطي الجيد سيكون النموذج الذي يحتوي على معامل ارتباط عالي (أقرب إلى 1 من 0) باستخدام طريقة انحدار المربعات الصغرى مع خط الانحدار. ✅ قم بتشغيل دفتر الملاحظات المرافق لهذا الدرس وانظر إلى مخطط الشهر مقابل السعر. هل تبدو البيانات التي تربط الشهر بالسعر لمبيعات القرع ذات ارتباط عالي أو منخفض، وفقًا لتفسيرك البصري للمخطط المبعثر؟ هل يتغير ذلك إذا استخدمت مقياسًا أكثر دقة بدلاً من `الشهر`، مثل *اليوم من السنة* (أي عدد الأيام منذ بداية السنة)؟ في الكود أدناه، سنفترض أننا قمنا بتنظيف البيانات، وحصلنا على إطار بيانات يسمى `new_pumpkins`، مشابه لما يلي: ID | Month | DayOfYear | Variety | City | Package | Low Price | High Price | Price ---|-------|-----------|---------|------|---------|-----------|------------|------- 70 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 15.0 | 15.0 | 13.636364 71 | 9 | 267 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 18.0 | 18.0 | 16.363636 72 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 18.0 | 18.0 | 16.363636 73 | 10 | 274 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 17.0 | 17.0 | 15.454545 74 | 10 | 281 | PIE TYPE | BALTIMORE | 1 1/9 bushel cartons | 15.0 | 15.0 | 13.636364 > الكود لتنظيف البيانات متوفر في [`notebook.ipynb`](../../../../2-Regression/3-Linear/notebook.ipynb). قمنا بتنفيذ نفس خطوات التنظيف كما في الدرس السابق، وقمنا بحساب عمود `DayOfYear` باستخدام التعبير التالي: ```python day_of_year = pd.to_datetime(pumpkins['Date']).apply(lambda dt: (dt-datetime(dt.year,1,1)).days) ``` الآن بعد أن أصبحت لديك فهم للرياضيات وراء الانحدار الخطي، دعنا ننشئ نموذج انحدار لنرى ما إذا كان بإمكاننا التنبؤ بأي حزمة من القرع ستحتوي على أفضل أسعار القرع. قد يرغب شخص يشتري القرع لحديقة قرع العطلات في هذه المعلومات ليتمكن من تحسين مشترياته من حزم القرع للحديقة. ## البحث عن الارتباط [](https://youtu.be/uoRq-lW2eQo "تعلّم الآلة للمبتدئين - البحث عن الارتباط: المفتاح للانحدار الخطي") > 🎥 انقر على الصورة أعلاه لمشاهدة فيديو قصير عن الارتباط. من الدرس السابق ربما لاحظت أن متوسط السعر للأشهر المختلفة يبدو كالتالي: هذا يشير إلى أنه يجب أن يكون هناك بعض الارتباط، ويمكننا محاولة تدريب نموذج انحدار خطي للتنبؤ بالعلاقة بين `الشهر` و `السعر`، أو بين `اليوم من السنة` و `السعر`. إليك المخطط المبعثر الذي يظهر العلاقة الأخيرة: دعونا نرى ما إذا كان هناك ارتباط باستخدام وظيفة `corr`: ```python print(new_pumpkins['Month'].corr(new_pumpkins['Price'])) print(new_pumpkins['DayOfYear'].corr(new_pumpkins['Price'])) ``` يبدو أن الارتباط صغير جدًا، -0.15 حسب `الشهر` و -0.17 حسب `اليوم من الشهر`، ولكن قد تكون هناك علاقة مهمة أخرى. يبدو أن هناك مجموعات مختلفة من الأسعار تتوافق مع أنواع مختلفة من القرع. لتأكيد هذه الفرضية، دعونا نرسم كل فئة من القرع باستخدام لون مختلف. من خلال تمرير معلمة `ax` إلى وظيفة الرسم المبعثر، يمكننا رسم جميع النقاط على نفس الرسم البياني: ```python ax=None colors = ['red','blue','green','yellow'] for i,var in enumerate(new_pumpkins['Variety'].unique()): df = new_pumpkins[new_pumpkins['Variety']==var] ax = df.plot.scatter('DayOfYear','Price',ax=ax,c=colors[i],label=var) ``` تشير تحقيقاتنا إلى أن النوع له تأثير أكبر على السعر الإجمالي من تاريخ البيع الفعلي. يمكننا رؤية ذلك باستخدام مخطط شريطي: ```python new_pumpkins.groupby('Variety')['Price'].mean().plot(kind='bar') ``` دعونا نركز في الوقت الحالي فقط على نوع واحد من القرع، وهو "نوع الفطيرة"، ونرى ما هو تأثير التاريخ على السعر: ```python pie_pumpkins = new_pumpkins[new_pumpkins['Variety']=='PIE TYPE'] pie_pumpkins.plot.scatter('DayOfYear','Price') ``` إذا قمنا الآن بحساب الارتباط بين `السعر` و `اليوم من السنة` باستخدام وظيفة `corr`، سنحصل على شيء مثل `-0.27` - مما يعني أن تدريب نموذج تنبؤي يبدو منطقيًا. > قبل تدريب نموذج الانحدار الخطي، من المهم التأكد من أن بياناتنا نظيفة. لا يعمل الانحدار الخطي جيدًا مع القيم المفقودة، لذا من المنطقي التخلص من جميع الخلايا الفارغة: ```python pie_pumpkins.dropna(inplace=True) pie_pumpkins.info() ``` نهج آخر سيكون ملء تلك القيم الفارغة بالقيم المتوسطة من العمود المقابل. ## الانحدار الخطي البسيط [](https://youtu.be/e4c_UP2fSjg "تعلّم الآلة للمبتدئين - الانحدار الخطي ومتعدد الحدود باستخدام Scikit-learn") > 🎥 انقر على الصورة أعلاه لمشاهدة فيديو قصير عن الانحدار الخطي ومتعدد الحدود. لتدريب نموذج الانحدار الخطي الخاص بنا، سنستخدم مكتبة **Scikit-learn**. ```python from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error from sklearn.model_selection import train_test_split ``` نبدأ بفصل قيم الإدخال (الميزات) والنتائج المتوقعة (التسمية) في مصفوفات numpy منفصلة: ```python X = pie_pumpkins['DayOfYear'].to_numpy().reshape(-1,1) y = pie_pumpkins['Price'] ``` > لاحظ أننا اضطررنا إلى تنفيذ `reshape` على بيانات الإدخال لكي يفهمها حزمة الانحدار الخطي بشكل صحيح. يتوقع الانحدار الخطي مصفوفة ثنائية الأبعاد كمدخل، حيث يمثل كل صف من المصفوفة متجهًا لميزات الإدخال. في حالتنا، نظرًا لأن لدينا مدخلًا واحدًا فقط - نحتاج إلى مصفوفة ذات شكل N×1، حيث N هو حجم مجموعة البيانات. ثم، نحتاج إلى تقسيم البيانات إلى مجموعات تدريب واختبار، حتى نتمكن من التحقق من صحة النموذج بعد التدريب: ```python X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) ``` أخيرًا، تدريب نموذج الانحدار الخطي الفعلي يستغرق فقط سطرين من الكود. نقوم بتعريف كائن `LinearRegression`، ونقوم بتدريبه على بياناتنا باستخدام طريقة `fit`: ```python lin_reg = LinearRegression() lin_reg.fit(X_train,y_train) ``` يحتوي كائن `LinearRegression` بعد عملية `fit` على جميع معاملات الانحدار، والتي يمكن الوصول إليها باستخدام خاصية `.coef_`. في حالتنا، هناك معامل واحد فقط، والذي يجب أن يكون حوالي `-0.017`. هذا يعني أن الأسعار تبدو وكأنها تنخفض قليلاً مع مرور الوقت، ولكن ليس كثيرًا، حوالي 2 سنت في اليوم. يمكننا أيضًا الوصول إلى نقطة تقاطع الانحدار مع المحور Y باستخدام `lin_reg.intercept_` - ستكون حوالي `21` في حالتنا، مما يشير إلى السعر في بداية السنة. لرؤية مدى دقة نموذجنا، يمكننا توقع الأسعار على مجموعة بيانات الاختبار، ثم قياس مدى قرب توقعاتنا من القيم المتوقعة. يمكن القيام بذلك باستخدام مقياس متوسط الخطأ التربيعي (MSE)، وهو متوسط جميع الفروقات المربعة بين القيمة المتوقعة والقيمة المتنبأ بها. ```python pred = lin_reg.predict(X_test) mse = np.sqrt(mean_squared_error(y_test,pred)) print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)') ``` يبدو أن الخطأ لدينا يتمحور حول نقطتين، أي حوالي 17%. ليس جيدًا جدًا. مؤشر آخر لجودة النموذج هو **معامل التحديد**، والذي يمكن الحصول عليه بهذه الطريقة: ```python score = lin_reg.score(X_train,y_train) print('Model determination: ', score) ``` إذا كانت القيمة 0، فهذا يعني أن النموذج لا يأخذ بيانات الإدخال في الاعتبار، ويعمل كـ *أسوأ متنبئ خطي*، وهو ببساطة متوسط ​​القيمة للنتيجة. أما إذا كانت القيمة 1، فهذا يعني أننا يمكننا التنبؤ بجميع النتائج المتوقعة بشكل مثالي. في حالتنا، معامل التحديد حوالي 0.06، وهو منخفض جدًا. يمكننا أيضًا رسم بيانات الاختبار مع خط الانحدار لنرى بشكل أفضل كيف يعمل الانحدار في حالتنا: ```python plt.scatter(X_test,y_test) plt.plot(X_test,pred) ``` ## الانحدار متعدد الحدود نوع آخر من الانحدار الخطي هو الانحدار متعدد الحدود. في بعض الأحيان تكون هناك علاقة خطية بين المتغيرات - كلما زاد حجم اليقطين، زاد السعر - ولكن في أحيان أخرى لا يمكن رسم هذه العلاقات كطائرة أو خط مستقيم. ✅ إليك [بعض الأمثلة](https://online.stat.psu.edu/stat501/lesson/9/9.8) على البيانات التي يمكن استخدام الانحدار متعدد الحدود معها. ألقِ نظرة أخرى على العلاقة بين التاريخ والسعر. هل يبدو هذا الرسم البياني وكأنه يجب تحليله بخط مستقيم؟ ألا يمكن أن تتقلب الأسعار؟ في هذه الحالة، يمكنك تجربة الانحدار متعدد الحدود. ✅ الحدوديات هي تعبيرات رياضية قد تتكون من متغير واحد أو أكثر ومعاملات. الانحدار متعدد الحدود ينشئ خطًا منحنيًا ليتناسب بشكل أفضل مع البيانات غير الخطية. في حالتنا، إذا قمنا بإضافة متغير `DayOfYear` المربع إلى بيانات الإدخال، يجب أن نتمكن من ملاءمة بياناتنا بمنحنى شبه مكافئ، والذي سيكون له حد أدنى في نقطة معينة خلال السنة. تتضمن مكتبة Scikit-learn واجهة [API للأنابيب](https://scikit-learn.org/stable/modules/generated/sklearn.pipeline.make_pipeline.html?highlight=pipeline#sklearn.pipeline.make_pipeline) لتجميع خطوات معالجة البيانات المختلفة معًا. **الأنبوب** هو سلسلة من **المقدّرين**. في حالتنا، سننشئ أنبوبًا يضيف أولاً ميزات متعددة الحدود إلى النموذج، ثم يدرب الانحدار: ```python from sklearn.preprocessing import PolynomialFeatures from sklearn.pipeline import make_pipeline pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression()) pipeline.fit(X_train,y_train) ``` استخدام `PolynomialFeatures(2)` يعني أننا سنضيف جميع الحدوديات من الدرجة الثانية من بيانات الإدخال. في حالتنا، هذا يعني فقط `DayOfYear`²، ولكن إذا كان لدينا متغيران مدخلان X و Y، فسيتم إضافة X²، XY و Y². يمكننا أيضًا استخدام حدوديات من درجات أعلى إذا أردنا. يمكن استخدام الأنابيب بنفس الطريقة التي يتم بها استخدام كائن `LinearRegression` الأصلي، أي يمكننا `fit` الأنبوب، ثم استخدام `predict` للحصول على نتائج التنبؤ. إليك الرسم البياني الذي يظهر بيانات الاختبار ومنحنى التقريب: باستخدام الانحدار متعدد الحدود، يمكننا الحصول على MSE أقل قليلاً ومعامل تحديد أعلى، ولكن ليس بشكل كبير. يجب أن نأخذ في الاعتبار ميزات أخرى! > يمكنك أن ترى أن أدنى أسعار اليقطين تُلاحظ في مكان ما حول عيد الهالوين. كيف يمكنك تفسير ذلك؟ 🎃 تهانينا، لقد أنشأت نموذجًا يمكنه المساعدة في التنبؤ بسعر فطائر اليقطين. ربما يمكنك تكرار نفس الإجراء لجميع أنواع اليقطين، ولكن سيكون ذلك مرهقًا. دعنا نتعلم الآن كيفية أخذ نوع اليقطين في الاعتبار في نموذجنا! ## الميزات الفئوية في العالم المثالي، نريد أن نكون قادرين على التنبؤ بالأسعار لأنواع مختلفة من اليقطين باستخدام نفس النموذج. ومع ذلك، فإن العمود `Variety` يختلف قليلاً عن الأعمدة مثل `Month`، لأنه يحتوي على قيم غير رقمية. تُعرف هذه الأعمدة بـ **الفئوية**. [](https://youtu.be/DYGliioIAE0 "تعلم الآلة للمبتدئين - التنبؤ بالميزات الفئوية باستخدام الانحدار الخطي") > 🎥 انقر على الصورة أعلاه للحصول على نظرة عامة قصيرة حول استخدام الميزات الفئوية. هنا يمكنك رؤية كيف يعتمد السعر المتوسط على النوع: لأخذ النوع في الاعتبار، نحتاج أولاً إلى تحويله إلى شكل رقمي، أو **ترميزه**. هناك عدة طرق يمكننا القيام بها: * **الترميز الرقمي البسيط** سيقوم ببناء جدول لأنواع مختلفة، ثم استبدال اسم النوع برقم في هذا الجدول. هذه ليست أفضل فكرة للانحدار الخطي، لأن الانحدار الخطي يأخذ القيمة الرقمية الفعلية للرقم، ويضيفها إلى النتيجة، مضروبًا بمعامل معين. في حالتنا، العلاقة بين رقم الفهرس والسعر غير خطية بوضوح، حتى لو تأكدنا من أن الأرقام مرتبة بطريقة معينة. * **الترميز الواحد الساخن** سيقوم باستبدال العمود `Variety` بأربعة أعمدة مختلفة، واحد لكل نوع. يحتوي كل عمود على `1` إذا كانت الصف المقابل من نوع معين، و`0` خلاف ذلك. هذا يعني أنه سيكون هناك أربعة معاملات في الانحدار الخطي، واحد لكل نوع من أنواع اليقطين، مسؤول عن "السعر الأساسي" (أو بالأحرى "السعر الإضافي") لذلك النوع المحدد. الكود أدناه يظهر كيف يمكننا ترميز النوع الواحد الساخن: ```python pd.get_dummies(new_pumpkins['Variety']) ``` ID | FAIRYTALE | MINIATURE | MIXED HEIRLOOM VARIETIES | PIE TYPE ----|-----------|-----------|--------------------------|---------- 70 | 0 | 0 | 0 | 1 71 | 0 | 0 | 0 | 1 ... | ... | ... | ... | ... 1738 | 0 | 1 | 0 | 0 1739 | 0 | 1 | 0 | 0 1740 | 0 | 1 | 0 | 0 1741 | 0 | 1 | 0 | 0 1742 | 0 | 1 | 0 | 0 لتدريب الانحدار الخطي باستخدام النوع المرمز الواحد الساخن كمدخل، نحتاج فقط إلى تهيئة بيانات `X` و `y` بشكل صحيح: ```python X = pd.get_dummies(new_pumpkins['Variety']) y = new_pumpkins['Price'] ``` بقية الكود هي نفسها التي استخدمناها أعلاه لتدريب الانحدار الخطي. إذا جربتها، سترى أن متوسط الخطأ التربيعي مشابه، ولكن نحصل على معامل تحديد أعلى بكثير (~77%). للحصول على تنبؤات أكثر دقة، يمكننا أخذ المزيد من الميزات الفئوية في الاعتبار، بالإضافة إلى الميزات الرقمية، مثل `Month` أو `DayOfYear`. للحصول على مصفوفة كبيرة من الميزات، يمكننا استخدام `join`: ```python X = pd.get_dummies(new_pumpkins['Variety']) \ .join(new_pumpkins['Month']) \ .join(pd.get_dummies(new_pumpkins['City'])) \ .join(pd.get_dummies(new_pumpkins['Package'])) y = new_pumpkins['Price'] ``` هنا نأخذ أيضًا في الاعتبار `City` ونوع `Package`، مما يعطينا MSE 2.84 (10%)، ومعامل تحديد 0.94! ## تجميع كل شيء معًا لإنشاء أفضل نموذج، يمكننا استخدام البيانات المجمعة (الميزات الفئوية المرمزة الواحد الساخن + الرقمية) من المثال أعلاه مع الانحدار متعدد الحدود. إليك الكود الكامل لراحتك: ```python # set up training data X = pd.get_dummies(new_pumpkins['Variety']) \ .join(new_pumpkins['Month']) \ .join(pd.get_dummies(new_pumpkins['City'])) \ .join(pd.get_dummies(new_pumpkins['Package'])) y = new_pumpkins['Price'] # make train-test split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) # setup and train the pipeline pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression()) pipeline.fit(X_train,y_train) # predict results for test data pred = pipeline.predict(X_test) # calculate MSE and determination mse = np.sqrt(mean_squared_error(y_test,pred)) print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)') score = pipeline.score(X_train,y_train) print('Model determination: ', score) ``` هذا يجب أن يعطينا أفضل معامل تحديد تقريبًا 97%، و MSE=2.23 (~8% خطأ في التنبؤ). | النموذج | MSE | معامل التحديد | |---------|-----|---------------| | `DayOfYear` خطي | 2.77 (17.2%) | 0.07 | | `DayOfYear` متعدد الحدود | 2.73 (17.0%) | 0.08 | | `Variety` خطي | 5.24 (19.7%) | 0.77 | | جميع الميزات خطي | 2.84 (10.5%) | 0.94 | | جميع الميزات متعدد الحدود | 2.23 (8.25%) | 0.97 | 🏆 أحسنت! لقد أنشأت أربعة نماذج انحدار في درس واحد، وحسّنت جودة النموذج إلى 97%. في القسم الأخير حول الانحدار، ستتعلم عن الانحدار اللوجستي لتحديد الفئات. --- ## 🚀التحدي اختبر عدة متغيرات مختلفة في هذا الدفتر لترى كيف تتوافق العلاقة مع دقة النموذج. ## [اختبار ما بعد المحاضرة](https://ff-quizzes.netlify.app/en/ml/) ## المراجعة والدراسة الذاتية في هذا الدرس تعلمنا عن الانحدار الخطي. هناك أنواع أخرى مهمة من الانحدار. اقرأ عن تقنيات Stepwise، Ridge، Lasso و Elasticnet. دورة جيدة للدراسة لتعلم المزيد هي [دورة التعلم الإحصائي من جامعة ستانفورد](https://online.stanford.edu/courses/sohs-ystatslearning-statistical-learning). ## الواجب [قم ببناء نموذج](assignment.md) --- **إخلاء المسؤولية**: تمت ترجمة هذا المستند باستخدام خدمة الترجمة الآلية [Co-op Translator](https://github.com/Azure/co-op-translator). بينما نسعى لتحقيق الدقة، يرجى العلم أن الترجمات الآلية قد تحتوي على أخطاء أو معلومات غير دقيقة. يجب اعتبار المستند الأصلي بلغته الأصلية هو المصدر الموثوق. للحصول على معلومات حساسة أو هامة، يُوصى بالاستعانة بترجمة بشرية احترافية. نحن غير مسؤولين عن أي سوء فهم أو تفسيرات خاطئة تنشأ عن استخدام هذه الترجمة.