# Previsão de séries temporais com ARIMA
Na lição anterior, você aprendeu um pouco sobre previsão de séries temporais e carregou um conjunto de dados que mostra as flutuações da carga elétrica ao longo de um período de tempo.
[](https://youtu.be/IUSk-YDau10 "Introdução ao ARIMA")
> 🎥 Clique na imagem acima para assistir a um vídeo: Uma breve introdução aos modelos ARIMA. O exemplo é feito em R, mas os conceitos são universais.
## [Questionário pré-aula](https://gray-sand-07a10f403.1.azurestaticapps.net/quiz/43/)
## Introdução
Nesta lição, você descobrirá uma maneira específica de construir modelos com [ARIMA: *A*uto*R*egressivo *I*ntegrado *M*édia *M*óvel](https://wikipedia.org/wiki/Autoregressive_integrated_moving_average). Os modelos ARIMA são particularmente adequados para ajustar dados que apresentam [não-estacionariedade](https://wikipedia.org/wiki/Stationary_process).
## Conceitos gerais
Para poder trabalhar com ARIMA, há alguns conceitos que você precisa conhecer:
- 🎓 **Estacionariedade**. Em um contexto estatístico, estacionariedade refere-se a dados cuja distribuição não muda quando deslocados no tempo. Dados não estacionários, portanto, mostram flutuações devido a tendências que precisam ser transformadas para serem analisadas. A sazonalidade, por exemplo, pode introduzir flutuações nos dados e pode ser eliminada por um processo de 'diferenciação sazonal'.
- 🎓 **[Diferenciação](https://wikipedia.org/wiki/Autoregressive_integrated_moving_average#Differencing)**. A diferenciação de dados, novamente em um contexto estatístico, refere-se ao processo de transformar dados não estacionários para torná-los estacionários, removendo sua tendência não constante. "A diferenciação remove as mudanças no nível de uma série temporal, eliminando tendência e sazonalidade e, consequentemente, estabilizando a média da série temporal." [Artigo de Shixiong et al](https://arxiv.org/abs/1904.07632)
## ARIMA no contexto de séries temporais
Vamos desmembrar as partes do ARIMA para entender melhor como ele nos ajuda a modelar séries temporais e a fazer previsões a partir delas.
- **AR - de AutoRegressivo**. Modelos autoregressivos, como o nome sugere, olham 'para trás' no tempo para analisar valores anteriores em seus dados e fazer suposições sobre eles. Esses valores anteriores são chamados de 'defasagens'. Um exemplo seria dados que mostram vendas mensais de lápis. O total de vendas de cada mês seria considerado uma 'variável em evolução' no conjunto de dados. Este modelo é construído à medida que "a variável de interesse em evolução é regredida em seus próprios valores defasados (ou seja, anteriores)." [wikipedia](https://wikipedia.org/wiki/Autoregressive_integrated_moving_average)
- **I - de Integrado**. Ao contrário dos modelos 'ARMA' semelhantes, o 'I' em ARIMA refere-se ao seu aspecto *[integrado](https://wikipedia.org/wiki/Order_of_integration)*. Os dados são 'integrados' quando passos de diferenciação são aplicados para eliminar a não-estacionariedade.
- **MA - de Média Móvel**. O aspecto de [média móvel](https://wikipedia.org/wiki/Moving-average_model) deste modelo refere-se à variável de saída que é determinada observando os valores atuais e passados das defasagens.
Em resumo: ARIMA é usado para fazer um modelo se ajustar à forma especial dos dados de séries temporais o mais próximo possível.
## Exercício - construir um modelo ARIMA
Abra a pasta [_/working_](https://github.com/microsoft/ML-For-Beginners/tree/main/7-TimeSeries/2-ARIMA/working) nesta lição e encontre o arquivo [_notebook.ipynb_](https://github.com/microsoft/ML-For-Beginners/blob/main/7-TimeSeries/2-ARIMA/working/notebook.ipynb).
1. Execute o notebook para carregar a biblioteca Python `statsmodels`; você precisará disso para os modelos ARIMA.
1. Carregue as bibliotecas necessárias.
1. Agora, carregue várias outras bibliotecas úteis para plotar dados:
```python
import os
import warnings
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime as dt
import math
from pandas.plotting import autocorrelation_plot
from statsmodels.tsa.statespace.sarimax import SARIMAX
from sklearn.preprocessing import MinMaxScaler
from common.utils import load_data, mape
from IPython.display import Image
%matplotlib inline
pd.options.display.float_format = '{:,.2f}'.format
np.set_printoptions(precision=2)
warnings.filterwarnings("ignore") # specify to ignore warning messages
```
1. Carregue os dados do arquivo `/data/energy.csv` em um dataframe do Pandas e dê uma olhada:
```python
energy = load_data('./data')[['load']]
energy.head(10)
```
1. Plote todos os dados de energia disponíveis de janeiro de 2012 a dezembro de 2014. Não deve haver surpresas, pois vimos esses dados na última lição:
```python
energy.plot(y='load', subplots=True, figsize=(15, 8), fontsize=12)
plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()
```
Agora, vamos construir um modelo!
### Criar conjuntos de dados de treinamento e teste
Agora que seus dados estão carregados, você pode separá-los em conjuntos de treino e teste. Você treinará seu modelo no conjunto de treino. Como de costume, após o modelo ter terminado de treinar, você avaliará sua precisão usando o conjunto de teste. Você precisa garantir que o conjunto de teste cubra um período posterior ao conjunto de treino para garantir que o modelo não obtenha informações de períodos futuros.
1. Alocar um período de dois meses de 1º de setembro a 31 de outubro de 2014 para o conjunto de treino. O conjunto de teste incluirá o período de dois meses de 1º de novembro a 31 de dezembro de 2014:
```python
train_start_dt = '2014-11-01 00:00:00'
test_start_dt = '2014-12-30 00:00:00'
```
Como esses dados refletem o consumo diário de energia, há um forte padrão sazonal, mas o consumo é mais semelhante ao consumo em dias mais recentes.
1. Visualize as diferenças:
```python
energy[(energy.index < test_start_dt) & (energy.index >= train_start_dt)][['load']].rename(columns={'load':'train'}) \
.join(energy[test_start_dt:][['load']].rename(columns={'load':'test'}), how='outer') \
.plot(y=['train', 'test'], figsize=(15, 8), fontsize=12)
plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()
```
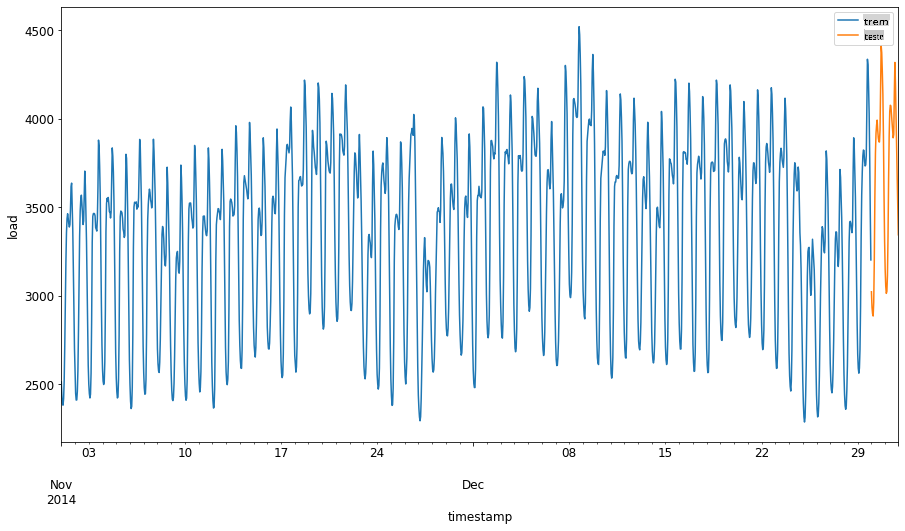
Portanto, usar uma janela de tempo relativamente pequena para treinar os dados deve ser suficiente.
> Nota: Como a função que usamos para ajustar o modelo ARIMA utiliza validação in-sample durante o ajuste, omitiremos os dados de validação.
### Preparar os dados para treinamento
Agora, você precisa preparar os dados para treinamento, realizando filtragem e escalonamento de seus dados. Filtre seu conjunto de dados para incluir apenas os períodos de tempo e colunas que você precisa, e escale para garantir que os dados sejam projetados no intervalo 0,1.
1. Filtre o conjunto de dados original para incluir apenas os períodos de tempo mencionados por conjunto e apenas a coluna necessária 'load' mais a data:
```python
train = energy.copy()[(energy.index >= train_start_dt) & (energy.index < test_start_dt)][['load']]
test = energy.copy()[energy.index >= test_start_dt][['load']]
print('Training data shape: ', train.shape)
print('Test data shape: ', test.shape)
```
Você pode ver a forma dos dados:
```output
Training data shape: (1416, 1)
Test data shape: (48, 1)
```
1. Escale os dados para que fiquem no intervalo (0, 1).
```python
scaler = MinMaxScaler()
train['load'] = scaler.fit_transform(train)
train.head(10)
```
1. Visualize os dados originais vs. os dados escalonados:
```python
energy[(energy.index >= train_start_dt) & (energy.index < test_start_dt)][['load']].rename(columns={'load':'original load'}).plot.hist(bins=100, fontsize=12)
train.rename(columns={'load':'scaled load'}).plot.hist(bins=100, fontsize=12)
plt.show()
```
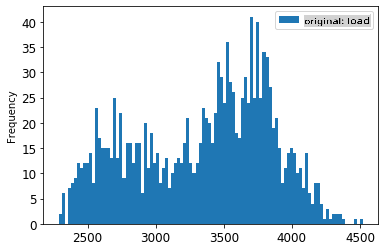
> Os dados originais
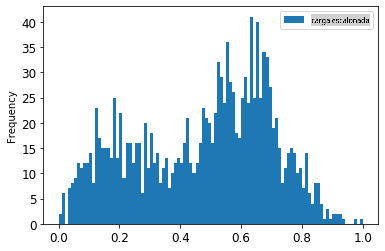
> Os dados escalonados
1. Agora que você calibrou os dados escalonados, pode escalar os dados de teste:
```python
test['load'] = scaler.transform(test)
test.head()
```
### Implementar ARIMA
É hora de implementar o ARIMA! Agora você usará a biblioteca `statsmodels` que você instalou anteriormente.
Agora você precisa seguir várias etapas:
1. Defina o modelo chamando `SARIMAX()` and passing in the model parameters: p, d, and q parameters, and P, D, and Q parameters.
2. Prepare the model for the training data by calling the fit() function.
3. Make predictions calling the `forecast()` function and specifying the number of steps (the `horizon`) to forecast.
> 🎓 What are all these parameters for? In an ARIMA model there are 3 parameters that are used to help model the major aspects of a time series: seasonality, trend, and noise. These parameters are:
`p`: the parameter associated with the auto-regressive aspect of the model, which incorporates *past* values.
`d`: the parameter associated with the integrated part of the model, which affects the amount of *differencing* (🎓 remember differencing 👆?) to apply to a time series.
`q`: the parameter associated with the moving-average part of the model.
> Note: If your data has a seasonal aspect - which this one does - , we use a seasonal ARIMA model (SARIMA). In that case you need to use another set of parameters: `P`, `D`, and `Q` which describe the same associations as `p`, `d`, and `q`, mas que correspondem aos componentes sazonais do modelo.
1. Comece definindo seu valor de horizonte preferido. Vamos tentar 3 horas:
```python
# Specify the number of steps to forecast ahead
HORIZON = 3
print('Forecasting horizon:', HORIZON, 'hours')
```
Selecionar os melhores valores para os parâmetros de um modelo ARIMA pode ser desafiador, pois é um pouco subjetivo e consome tempo. Você pode considerar usar uma biblioteca `auto_arima()` function from the [`pyramid`](https://alkaline-ml.com/pmdarima/0.9.0/modules/generated/pyramid.arima.auto_arima.html),
1. Por enquanto, tente algumas seleções manuais para encontrar um bom modelo.
```python
order = (4, 1, 0)
seasonal_order = (1, 1, 0, 24)
model = SARIMAX(endog=train, order=order, seasonal_order=seasonal_order)
results = model.fit()
print(results.summary())
```
Uma tabela de resultados é impressa.
Você construiu seu primeiro modelo! Agora precisamos encontrar uma maneira de avaliá-lo.
### Avalie seu modelo
Para avaliar seu modelo, você pode realizar a chamada validação `walk forward`. Na prática, os modelos de séries temporais são re-treinados cada vez que novos dados se tornam disponíveis. Isso permite que o modelo faça a melhor previsão em cada passo de tempo.
Começando no início da série temporal usando essa técnica, treine o modelo no conjunto de dados de treino. Em seguida, faça uma previsão no próximo passo de tempo. A previsão é avaliada em relação ao valor conhecido. O conjunto de treino é então expandido para incluir o valor conhecido e o processo é repetido.
> Nota: Você deve manter a janela do conjunto de treino fixa para um treinamento mais eficiente, de modo que toda vez que você adicionar uma nova observação ao conjunto de treino, você remova a observação do início do conjunto.
Esse processo fornece uma estimativa mais robusta de como o modelo se comportará na prática. No entanto, isso vem com o custo computacional de criar tantos modelos. Isso é aceitável se os dados forem pequenos ou se o modelo for simples, mas pode ser um problema em grande escala.
A validação walk-forward é o padrão ouro da avaliação de modelos de séries temporais e é recomendada para seus próprios projetos.
1. Primeiro, crie um ponto de dados de teste para cada passo do HORIZON.
```python
test_shifted = test.copy()
for t in range(1, HORIZON+1):
test_shifted['load+'+str(t)] = test_shifted['load'].shift(-t, freq='H')
test_shifted = test_shifted.dropna(how='any')
test_shifted.head(5)
```
| | | load | load+1 | load+2 |
| ---------- | -------- | ---- | ------ | ------ |
| 2014-12-30 | 00:00:00 | 0.33 | 0.29 | 0.27 |
| 2014-12-30 | 01:00:00 | 0.29 | 0.27 | 0.27 |
| 2014-12-30 | 02:00:00 | 0.27 | 0.27 | 0.30 |
| 2014-12-30 | 03:00:00 | 0.27 | 0.30 | 0.41 |
| 2014-12-30 | 04:00:00 | 0.30 | 0.41 | 0.57 |
Os dados são deslocados horizontalmente de acordo com seu ponto de horizonte.
1. Faça previsões em seus dados de teste usando essa abordagem de janela deslizante em um loop do tamanho do comprimento dos dados de teste:
```python
%%time
training_window = 720 # dedicate 30 days (720 hours) for training
train_ts = train['load']
test_ts = test_shifted
history = [x for x in train_ts]
history = history[(-training_window):]
predictions = list()
order = (2, 1, 0)
seasonal_order = (1, 1, 0, 24)
for t in range(test_ts.shape[0]):
model = SARIMAX(endog=history, order=order, seasonal_order=seasonal_order)
model_fit = model.fit()
yhat = model_fit.forecast(steps = HORIZON)
predictions.append(yhat)
obs = list(test_ts.iloc[t])
# move the training window
history.append(obs[0])
history.pop(0)
print(test_ts.index[t])
print(t+1, ': predicted =', yhat, 'expected =', obs)
```
Você pode observar o treinamento ocorrendo:
```output
2014-12-30 00:00:00
1 : predicted = [0.32 0.29 0.28] expected = [0.32945389435989236, 0.2900626678603402, 0.2739480752014323]
2014-12-30 01:00:00
2 : predicted = [0.3 0.29 0.3 ] expected = [0.2900626678603402, 0.2739480752014323, 0.26812891674127126]
2014-12-30 02:00:00
3 : predicted = [0.27 0.28 0.32] expected = [0.2739480752014323, 0.26812891674127126, 0.3025962399283795]
```
1. Compare as previsões com a carga real:
```python
eval_df = pd.DataFrame(predictions, columns=['t+'+str(t) for t in range(1, HORIZON+1)])
eval_df['timestamp'] = test.index[0:len(test.index)-HORIZON+1]
eval_df = pd.melt(eval_df, id_vars='timestamp', value_name='prediction', var_name='h')
eval_df['actual'] = np.array(np.transpose(test_ts)).ravel()
eval_df[['prediction', 'actual']] = scaler.inverse_transform(eval_df[['prediction', 'actual']])
eval_df.head()
```
Saída
| | | timestamp | h | previsão | real |
| --- | ---------- | --------- | --- | ---------- | -------- |
| 0 | 2014-12-30 | 00:00:00 | t+1 | 3,008.74 | 3,023.00 |
| 1 | 2014-12-30 | 01:00:00 | t+1 | 2,955.53 | 2,935.00 |
| 2 | 2014-12-30 | 02:00:00 | t+1 | 2,900.17 | 2,899.00 |
| 3 | 2014-12-30 | 03:00:00 | t+1 | 2,917.69 | 2,886.00 |
| 4 | 2014-12-30 | 04:00:00 | t+1 | 2,946.99 | 2,963.00 |
Observe a previsão dos dados horários, comparada à carga real. Quão precisa é essa previsão?
### Verifique a precisão do modelo
Verifique a precisão do seu modelo testando seu erro percentual absoluto médio (MAPE) em todas as previsões.
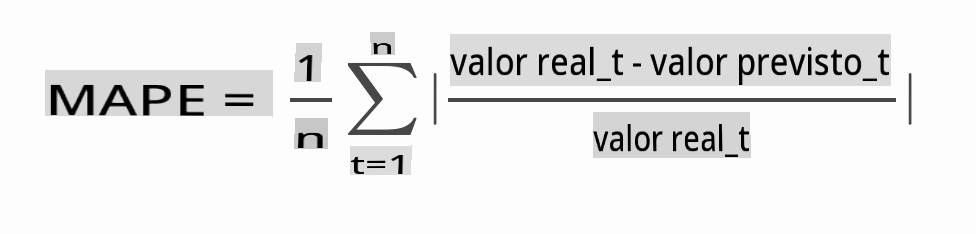
> **🧮 Mostre-me a matemática**
>
> 
>
> [MAPE](https://www.linkedin.com/pulse/what-mape-mad-msd-time-series-allameh-statistics/) é usado para mostrar a precisão da previsão como uma razão definida pela fórmula acima. A diferença entre realt e previstot é dividida pela realt. "O valor absoluto nesse cálculo é somado para cada ponto previsto no tempo e dividido pelo número de pontos ajustados n." [wikipedia](https://wikipedia.org/wiki/Mean_absolute_percentage_error)
1. Expresse a equação em código:
```python
if(HORIZON > 1):
eval_df['APE'] = (eval_df['prediction'] - eval_df['actual']).abs() / eval_df['actual']
print(eval_df.groupby('h')['APE'].mean())
```
1. Calcule o MAPE de um passo:
```python
print('One step forecast MAPE: ', (mape(eval_df[eval_df['h'] == 't+1']['prediction'], eval_df[eval_df['h'] == 't+1']['actual']))*100, '%')
```
MAPE da previsão de um passo: 0.5570581332313952 %
1. Imprima o MAPE da previsão de múltiplos passos:
```python
print('Multi-step forecast MAPE: ', mape(eval_df['prediction'], eval_df['actual'])*100, '%')
```
```output
Multi-step forecast MAPE: 1.1460048657704118 %
```
Um número baixo é o ideal: considere que uma previsão que tem um MAPE de 10 está errada em 10%.
1. Mas, como sempre, é mais fácil ver esse tipo de medição de precisão visualmente, então vamos plotá-la:
```python
if(HORIZON == 1):
## Plotting single step forecast
eval_df.plot(x='timestamp', y=['actual', 'prediction'], style=['r', 'b'], figsize=(15, 8))
else:
## Plotting multi step forecast
plot_df = eval_df[(eval_df.h=='t+1')][['timestamp', 'actual']]
for t in range(1, HORIZON+1):
plot_df['t+'+str(t)] = eval_df[(eval_df.h=='t+'+str(t))]['prediction'].values
fig = plt.figure(figsize=(15, 8))
ax = plt.plot(plot_df['timestamp'], plot_df['actual'], color='red', linewidth=4.0)
ax = fig.add_subplot(111)
for t in range(1, HORIZON+1):
x = plot_df['timestamp'][(t-1):]
y = plot_df['t+'+str(t)][0:len(x)]
ax.plot(x, y, color='blue', linewidth=4*math.pow(.9,t), alpha=math.pow(0.8,t))
ax.legend(loc='best')
plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()
```
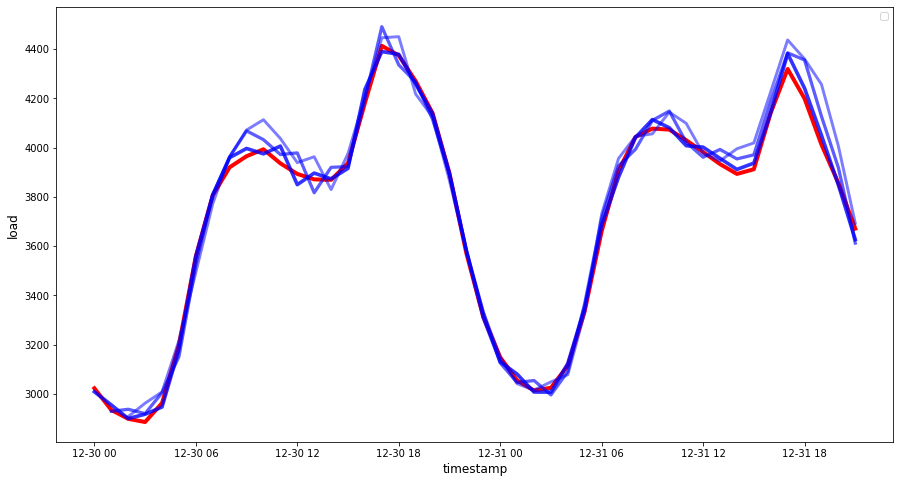
🏆 Um gráfico muito bonito, mostrando um modelo com boa precisão. Muito bem!
---
## 🚀Desafio
Explore as maneiras de testar a precisão de um Modelo de Série Temporal. Abordamos o MAPE nesta lição, mas existem outros métodos que você poderia usar? Pesquise-os e anote-os. Um documento útil pode ser encontrado [aqui](https://otexts.com/fpp2/accuracy.html)
## [Questionário pós-aula](https://gray-sand-07a10f403.1.azurestaticapps.net/quiz/44/)
## Revisão e Estudo Autônomo
Esta lição aborda apenas os conceitos básicos da Previsão de Séries Temporais com ARIMA. Reserve um tempo para aprofundar seu conhecimento explorando [este repositório](https://microsoft.github.io/forecasting/) e seus vários tipos de modelos para aprender outras maneiras de construir modelos de Séries Temporais.
## Tarefa
[Um novo modelo ARIMA](assignment.md)
**Aviso**:
Este documento foi traduzido utilizando serviços de tradução automática baseados em IA. Embora nos esforcemos pela precisão, esteja ciente de que traduções automatizadas podem conter erros ou imprecisões. O documento original em sua língua nativa deve ser considerado a fonte autoritativa. Para informações críticas, recomenda-se a tradução profissional feita por humanos. Não nos responsabilizamos por quaisquer mal-entendidos ou interpretações errôneas decorrentes do uso desta tradução.