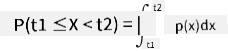|
|
2 weeks ago | |
|---|---|---|
| .. | ||
| solution | 2 weeks ago | |
| README.md | 2 weeks ago | |
| assignment.ipynb | 2 weeks ago | |
| assignment.md | 4 weeks ago | |
| notebook.ipynb | 2 weeks ago | |
README.md
统计与概率简要介绍
 |
|---|
| 统计与概率 - 由 @nitya 绘制的速记图 |
统计学和概率论是数学中两个密切相关的领域,与数据科学高度相关。虽然在没有深厚数学知识的情况下也可以处理数据,但了解一些基本概念仍然是有益的。在这里,我们将提供一个简短的介绍,帮助您入门。
课前测验
概率与随机变量
概率 是一个介于 0 和 1 之间的数字,用来表示某个 事件 的可能性。它定义为正结果(导致事件发生的结果)的数量除以总结果数量,前提是所有结果的可能性相等。例如,当我们掷骰子时,得到偶数的概率是 3/6 = 0.5。
谈到事件时,我们使用 随机变量。例如,表示掷骰子时得到的数字的随机变量可以取值 1 到 6。1 到 6 的数字集合称为 样本空间。我们可以讨论随机变量取某个值的概率,例如 P(X=3)=1/6。
上述例子中的随机变量称为 离散型,因为它有一个可计数的样本空间,即可以枚举的单独值。有些情况下,样本空间是实数范围或整个实数集。这类变量称为 连续型。一个很好的例子是公交车到达的时间。
概率分布
对于离散随机变量,可以通过函数 P(X) 简单地描述每个事件的概率。对于样本空间 S 中的每个值 s,它会给出一个介于 0 和 1 之间的数字,并且所有事件的 P(X=s) 值的总和为 1。
最著名的离散分布是 均匀分布,其中样本空间有 N 个元素,每个元素的概率相等,为 1/N。
描述连续变量的概率分布更为复杂,这些变量的值来自某个区间 [a,b] 或整个实数集 ℝ。考虑公交车到达时间的情况。实际上,对于每个确切的到达时间 t,公交车恰好在该时间到达的概率是 0!
现在您知道了概率为 0 的事件是会发生的,而且非常频繁!至少每次公交车到达时都是如此!
我们只能讨论变量落入某个值区间的概率,例如 P(t1≤X<t2)。在这种情况下,概率分布由 概率密度函数 p(x) 描述,其满足:
连续型均匀分布是均匀分布的连续版本,定义在有限区间内。值 X 落入长度为 l 的区间的概率与 l 成正比,最大为 1。
另一个重要的分布是 正态分布,我们将在下面详细讨论。
均值、方差与标准差
假设我们从随机变量 X 中抽取了 n 个样本:x1, x2, ..., xn。我们可以用传统方式定义序列的 均值(或 算术平均值)为 (x1+x2+...+xn)/n。当样本量增加(即 n→∞),我们将得到分布的均值(也称为 期望值)。我们用 E(x) 表示期望值。
可以证明,对于任何离散分布,其值为 {x1, x2, ..., xN},对应的概率为 p1, p2, ..., pN,期望值为 E(X)=x1p1+x2p2+...+xNpN。
为了确定值的分布范围,我们可以计算方差 σ2 = ∑(xi - μ)2/n,其中 μ 是序列的均值。值 σ 称为 标准差,而 σ2 称为 方差。
众数、中位数与四分位数
有时,均值并不能充分代表数据的“典型”值。例如,当存在一些极端值完全超出范围时,它们可能会影响均值。另一个很好的指标是 中位数,即一半数据点低于该值,另一半高于该值。
为了帮助我们理解数据分布,可以讨论 四分位数:
- 第一四分位数(Q1):25% 的数据低于该值
- 第三四分位数(Q3):75% 的数据低于该值
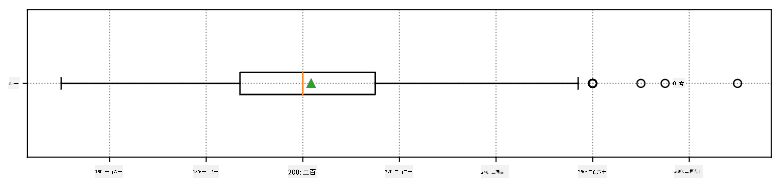
我们可以用一个称为 箱形图 的图表来直观表示中位数和四分位数之间的关系:

在这里,我们还计算了 四分位距 IQR=Q3-Q1,以及所谓的 异常值——位于区间 [Q1-1.5IQR,Q3+1.5IQR] 之外的值。
对于包含少量可能值的有限分布,一个好的“典型”值是出现频率最高的值,称为 众数。它通常应用于分类数据,例如颜色。考虑一种情况,我们有两组人——一组强烈偏爱红色,另一组偏爱蓝色。如果我们用数字编码颜色,最喜欢的颜色的均值可能会落在橙色-绿色光谱之间,这并不能反映任何一组的实际偏好。然而,众数可能是其中一种颜色,或者两种颜色(如果投票人数相等,在这种情况下我们称样本为 多众型)。
真实世界数据
当我们分析真实世界的数据时,它们通常不是严格意义上的随机变量,因为我们并未进行未知结果的实验。例如,考虑一组棒球运动员及其身体数据,如身高、体重和年龄。这些数字并不完全随机,但我们仍然可以应用相同的数学概念。例如,一组人的体重可以被视为从某个随机变量中抽取的一组值。以下是来自 美国职业棒球大联盟 的实际棒球运动员体重序列,数据来源于 此数据集(为方便起见,仅显示前 20 个值):
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
注意:要查看使用此数据集的示例,请查看 配套笔记本。本课程中还有许多挑战,您可以通过向该笔记本添加代码来完成它们。如果您不确定如何操作数据,请不要担心——我们稍后会回到使用 Python 处理数据的部分。如果您不知道如何在 Jupyter Notebook 中运行代码,请查看 这篇文章。
以下是显示我们数据的均值、中位数和四分位数的箱形图:
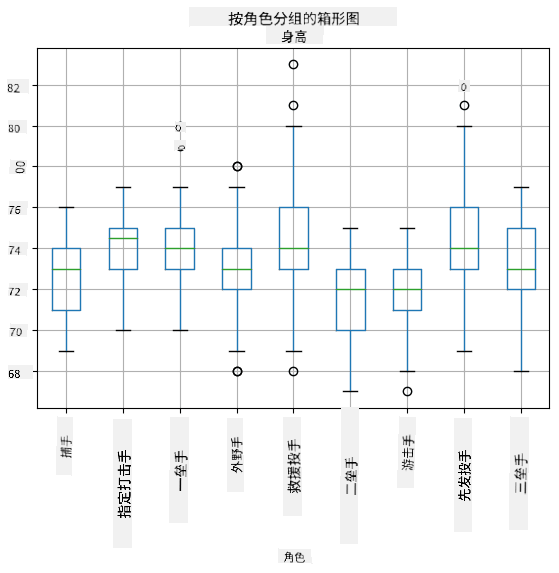
由于我们的数据包含关于不同球员 角色 的信息,我们还可以按角色绘制箱形图——这将帮助我们了解参数值在不同角色之间的差异。这次我们考虑身高:
此图表表明,平均而言,一垒手的身高高于二垒手的身高。在本课程后面,我们将学习如何更正式地验证这一假设,以及如何证明我们的数据在统计上显著。
在处理真实世界数据时,我们假设所有数据点是从某个概率分布中抽取的样本。这个假设使我们能够应用机器学习技术并构建有效的预测模型。
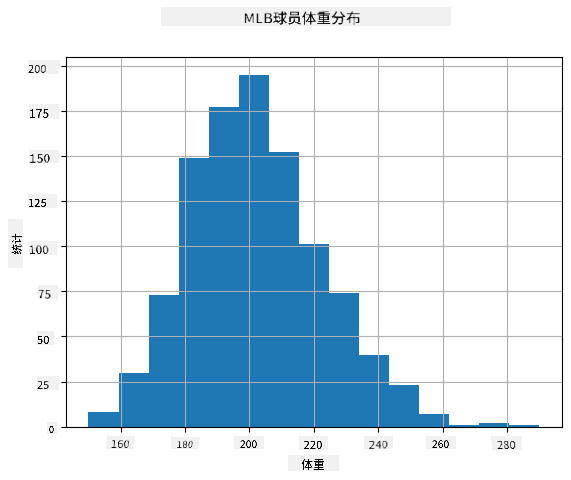
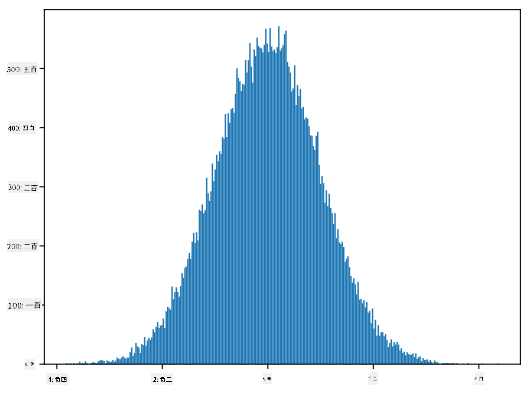
为了查看我们数据的分布,我们可以绘制一个称为 直方图 的图表。X 轴包含多个不同的体重区间(即 箱),而 Y 轴显示我们的随机变量样本落入某个区间的次数。
从这个直方图可以看出,所有值都集中在某个平均体重附近,离平均体重越远,出现该体重值的次数越少。也就是说,棒球运动员的体重与平均体重差异很大的可能性非常小。体重的方差显示了体重与平均体重可能的差异程度。
如果我们取其他人(非棒球联盟成员)的体重,分布可能会有所不同。然而,分布的形状会保持一致,但均值和方差会发生变化。因此,如果我们在棒球运动员上训练模型,当应用于大学学生时可能会产生错误结果,因为底层分布不同。
正态分布
我们上面看到的体重分布非常典型,许多真实世界的测量值遵循相同类型的分布,但均值和方差不同。这种分布称为 正态分布,在统计学中具有非常重要的作用。
使用正态分布是生成潜在棒球运动员随机体重的正确方法。一旦我们知道均值 mean 和标准差 std,我们可以通过以下方式生成 1000 个体重样本:
samples = np.random.normal(mean,std,1000)
如果我们绘制生成样本的直方图,我们会看到与上图非常相似的图像。如果我们增加样本数量和箱数量,我们可以生成更接近理想的正态分布图像:
均值=0,标准差=1 的正态分布
置信区间
当我们谈论棒球运动员的体重时,我们假设存在某个 随机变量 W,它对应于所有棒球运动员体重的理想概率分布(即 总体)。我们的体重序列对应于所有棒球运动员的一个子集,我们称之为 样本。一个有趣的问题是,我们能否知道 W 的分布参数,即总体的均值和方差?
最简单的答案是计算样本的均值和方差。然而,可能发生的情况是我们的随机样本不能准确代表完整总体。因此,谈论 置信区间 是有意义的。
置信区间 是根据我们的样本估计总体真实均值的范围,其准确性具有一定的概率(或 置信水平)。
假设我们有一个样本 X
1, ..., Xn 来自我们的分布。每次从分布中抽取样本时,我们都会得到不同的均值 μ。因此,μ 可以被视为一个随机变量。一个置信度为 p 的 置信区间 是一对值 (Lp, Rp),使得 P(Lp≤μ≤Rp) = p,即测得的均值落在该区间内的概率等于 p。
详细讨论如何计算这些置信区间超出了我们的简短介绍范围。更多细节可以参考 维基百科。简而言之,我们定义了计算样本均值相对于总体真实均值的分布,这被称为 学生分布。
有趣的事实:学生分布以数学家 William Sealy Gosset 的笔名 "Student" 命名。他在 Guinness 啤酒厂工作,根据一种说法,他的雇主不希望公众知道他们使用统计测试来确定原材料的质量。
如果我们想以置信度 p 估计总体均值 μ,我们需要取学生分布 A 的 (1-p)/2 分位数,这可以从表中查得,或者通过统计软件(如 Python、R 等)的内置函数计算。然后 μ 的区间为 X±A*D/√n,其中 X 是样本的均值,D 是标准差。
注意:我们还省略了一个重要概念 自由度 的讨论,这在学生分布中非常重要。您可以参考更完整的统计学书籍以更深入地理解这一概念。
关于体重和身高的置信区间计算示例可以在 配套笔记本 中找到。
| p | 体重均值 |
|---|---|
| 0.85 | 201.73±0.94 |
| 0.90 | 201.73±1.08 |
| 0.95 | 201.73±1.28 |
请注意,置信概率越高,置信区间越宽。
假设检验
在我们的棒球运动员数据集中,有不同的球员角色,可以总结如下(查看 配套笔记本 以了解如何计算此表):
| 角色 | 身高 | 体重 | 数量 |
|---|---|---|---|
| 捕手 | 72.723684 | 204.328947 | 76 |
| 指定击球手 | 74.222222 | 220.888889 | 18 |
| 一垒手 | 74.000000 | 213.109091 | 55 |
| 外野手 | 73.010309 | 199.113402 | 194 |
| 救援投手 | 74.374603 | 203.517460 | 315 |
| 二垒手 | 71.362069 | 184.344828 | 58 |
| 游击手 | 71.903846 | 182.923077 | 52 |
| 先发投手 | 74.719457 | 205.163636 | 221 |
| 三垒手 | 73.044444 | 200.955556 | 45 |
我们可以注意到,一垒手的平均身高高于二垒手。因此,我们可能会得出结论:一垒手比二垒手高。
这个陈述被称为 假设,因为我们并不知道这一事实是否确实为真。
然而,我们并不总是能轻易得出这个结论。从上面的讨论中我们知道,每个均值都有一个相关的置信区间,因此这种差异可能只是统计误差。我们需要更正式的方法来检验我们的假设。
让我们分别计算一垒手和二垒手身高的置信区间:
| 置信度 | 一垒手 | 二垒手 |
|---|---|---|
| 0.85 | 73.62..74.38 | 71.04..71.69 |
| 0.90 | 73.56..74.44 | 70.99..71.73 |
| 0.95 | 73.47..74.53 | 70.92..71.81 |
我们可以看到,在任何置信度下,这些区间都没有重叠。这证明了一垒手比二垒手高的假设。
更正式地说,我们要解决的问题是确定 两个概率分布是否相同,或者至少它们的参数是否相同。根据分布的不同,我们需要使用不同的检验方法。如果我们知道分布是正态分布,我们可以应用 学生 t 检验。
在学生 t 检验中,我们计算所谓的 t 值,它表示均值之间的差异,同时考虑方差。研究表明,t 值服从 学生分布,这使我们能够为给定的置信水平 p 找到阈值(可以通过计算或查阅数值表获得)。然后我们将 t 值与该阈值进行比较,以接受或拒绝假设。
在 Python 中,我们可以使用 SciPy 包,其中包括 ttest_ind 函数(以及许多其他有用的统计函数!)。它为我们计算 t 值,并反向查找置信 p 值,这样我们只需查看置信度即可得出结论。
例如,我们比较一垒手和二垒手身高的结果如下:
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
T-value = 7.65
P-value: 9.137321189738925e-12
在我们的例子中,p 值非常低,这意味着有强有力的证据支持一垒手更高。
此外,还有其他类型的假设我们可能想要检验,例如:
- 验证某个样本是否服从某种分布。在我们的例子中,我们假设身高服从正态分布,但这需要正式的统计验证。
- 验证样本的均值是否与某个预定义值相符。
- 比较多个样本的均值(例如,不同年龄组的幸福感水平差异)。
大数法则和中心极限定理
正态分布如此重要的原因之一是 中心极限定理。假设我们有一个独立的 N 个值 X1, ..., XN 的大样本,这些值来自任何分布,均值为 μ,方差为 σ2。那么,当 N 足够大时(换句话说,当 N→∞),均值 ΣiXi 将服从正态分布,均值为 μ,方差为 σ2/N。
另一种解释中心极限定理的方法是,无论分布如何,当你计算任意随机变量值之和的均值时,最终都会得到正态分布。
从中心极限定理还可以得出,当 N→∞ 时,样本均值等于 μ 的概率趋于 1。这被称为 大数法则。
协方差与相关性
数据科学的任务之一是发现数据之间的关系。当两个序列在同一时间表现出相似的行为时,我们称它们 相关,即它们要么同时上升/下降,要么一个序列上升时另一个下降,反之亦然。换句话说,这两个序列之间似乎存在某种关系。
相关性并不一定表示两个序列之间存在因果关系;有时两个变量可能依赖于某个外部原因,或者它们的相关性纯属偶然。然而,强烈的数学相关性是两个变量某种程度上相关的良好指示。
从数学上讲,显示两个随机变量之间关系的主要概念是 协方差,其计算公式为:Cov(X,Y) = E[(X-E(X))(Y-E(Y))]。我们计算两个变量偏离其均值的偏差,然后将这些偏差相乘。如果两个变量一起偏离,乘积将始终为正值,最终得到正协方差。如果两个变量不同步偏离(即一个低于平均值时另一个高于平均值),我们将始终得到负值,最终得到负协方差。如果偏差无关,它们将大致相加为零。
协方差的绝对值并不能告诉我们相关性的强弱,因为它取决于实际值的大小。为了归一化,我们可以将协方差除以两个变量的标准差,得到 相关性。相关性的好处是它始终在 [-1,1] 范围内,其中 1 表示强正相关,-1 表示强负相关,0 表示完全无相关(变量独立)。
示例:我们可以计算棒球运动员数据集中体重和身高之间的相关性:
print(np.corrcoef(weights,heights))
结果,我们得到如下 相关性矩阵:
array([[1. , 0.52959196],
[0.52959196, 1. ]])
相关性矩阵 C 可以为任意数量的输入序列 S1, ..., Sn 计算。Cij 的值是 Si 和 Sj 之间的相关性,对角线元素始终为 1(即 Si 的自相关性)。
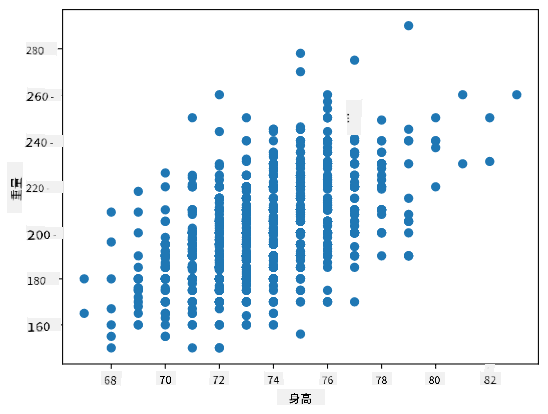
在我们的例子中,值 0.53 表明一个人的体重和身高之间存在一定的相关性。我们还可以绘制一个散点图,将一个值与另一个值进行比较,以直观地观察关系:
更多关于相关性和协方差的示例可以在 配套笔记本 中找到。
总结
在本节中,我们学习了:
- 数据的基本统计属性,例如均值、方差、众数和四分位数
- 随机变量的不同分布,包括正态分布
- 如何找到不同属性之间的相关性
- 如何使用数学和统计学的严谨工具来验证一些假设
- 如何根据数据样本计算随机变量的置信区间
虽然这绝不是概率和统计学中所有主题的详尽列表,但它应该足以为您进入本课程打下良好的基础。
🚀 挑战
使用笔记本中的示例代码测试以下假设:
- 一垒手比二垒手年龄更大
- 一垒手比三垒手更高
- 游击手比二垒手更高
课后测验
复习与自学
概率和统计学是一个非常广泛的主题,它值得开设一门独立的课程。如果您有兴趣深入学习理论,可以继续阅读以下书籍:
- 纽约大学 Carlos Fernandez-Granda 的优秀讲义 数据科学的概率与统计(在线可用)
- Peter 和 Andrew Bruce. 数据科学实用统计 [R 示例代码]。
- James D. Miller. 数据科学统计学 [R 示例代码]
作业
致谢
本课程由 Dmitry Soshnikov 倾情创作。
免责声明:
本文档使用AI翻译服务Co-op Translator进行翻译。尽管我们努力确保准确性,但请注意,自动翻译可能包含错误或不准确之处。应以原始语言的文档作为权威来源。对于关键信息,建议使用专业人工翻译。对于因使用本翻译而引起的任何误解或误读,我们概不负责。