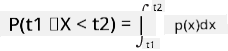|
|
2 weeks ago | |
|---|---|---|
| .. | ||
| solution | 2 weeks ago | |
| README.md | 2 weeks ago | |
| assignment.ipynb | 2 weeks ago | |
| assignment.md | 4 weeks ago | |
| notebook.ipynb | 2 weeks ago | |
README.md
En kort introduktion till statistik och sannolikhet
 |
|---|
| Statistik och sannolikhet - Sketchnote av @nitya |
Statistik och sannolikhetsteori är två nära besläktade områden inom matematiken som är mycket relevanta för datavetenskap. Det är möjligt att arbeta med data utan djupa kunskaper i matematik, men det är ändå bättre att känna till åtminstone några grundläggande begrepp. Här presenterar vi en kort introduktion som hjälper dig att komma igång.
Quiz före föreläsningen
Sannolikhet och slumpmässiga variabler
Sannolikhet är ett tal mellan 0 och 1 som uttrycker hur sannolikt en händelse är. Den definieras som antalet positiva utfall (som leder till händelsen), dividerat med det totala antalet utfall, givet att alla utfall är lika sannolika. Till exempel, när vi kastar en tärning, är sannolikheten att vi får ett jämnt tal 3/6 = 0,5.
När vi pratar om händelser använder vi slumpmässiga variabler. Till exempel, den slumpmässiga variabeln som representerar ett tal som erhålls vid ett tärningskast skulle anta värden från 1 till 6. Mängden av tal från 1 till 6 kallas utfallsrum. Vi kan prata om sannolikheten att en slumpmässig variabel antar ett visst värde, till exempel P(X=3)=1/6.
Den slumpmässiga variabeln i det tidigare exemplet kallas diskret, eftersom den har ett räkneligt utfallsrum, det vill säga det finns separata värden som kan numreras. Det finns fall där utfallsrummet är ett intervall av reella tal, eller hela mängden av reella tal. Sådana variabler kallas kontinuerliga. Ett bra exempel är tiden när bussen anländer.
Sannolikhetsfördelning
För diskreta slumpmässiga variabler är det enkelt att beskriva sannolikheten för varje händelse med en funktion P(X). För varje värde s från utfallsrummet S ger den ett tal mellan 0 och 1, så att summan av alla värden av P(X=s) för alla händelser blir 1.
Den mest kända diskreta fördelningen är likformig fördelning, där det finns ett utfallsrum med N element, med lika sannolikhet 1/N för vart och ett av dem.
Det är svårare att beskriva sannolikhetsfördelningen för en kontinuerlig variabel, med värden från ett intervall [a,b], eller hela mängden av reella tal ℝ. Tänk på fallet med busstider. Faktum är att för varje exakt ankomsttid t är sannolikheten att en buss anländer exakt vid den tiden 0!
Nu vet du att händelser med sannolikhet 0 inträffar, och väldigt ofta! Åtminstone varje gång bussen kommer!
Vi kan bara prata om sannolikheten att en variabel faller inom ett givet intervall av värden, t.ex. P(t1≤X<t2). I detta fall beskrivs sannolikhetsfördelningen av en sannolikhetstäthetsfunktion p(x), sådan att
En kontinuerlig analog till likformig fördelning kallas kontinuerligt likformig, som definieras på ett ändligt intervall. Sannolikheten att värdet X faller inom ett intervall av längd l är proportionell mot l och stiger upp till 1.
En annan viktig fördelning är normalfördelning, som vi kommer att prata mer om nedan.
Medelvärde, varians och standardavvikelse
Anta att vi drar en sekvens av n stickprov från en slumpmässig variabel X: x1, x2, ..., xn. Vi kan definiera medelvärde (eller aritmetiskt medelvärde) för sekvensen på det traditionella sättet som (x1+x2+xn)/n. När vi ökar stickprovets storlek (dvs. tar gränsvärdet med n→∞), får vi medelvärdet (även kallat förväntat värde) för fördelningen. Vi betecknar förväntat värde med E(x).
Det kan visas att för varje diskret fördelning med värden {x1, x2, ..., xN} och motsvarande sannolikheter p1, p2, ..., pN, skulle förväntat värde vara E(X)=x1p1+x2p2+...+xNpN.
För att identifiera hur spridda värdena är kan vi beräkna variansen σ2 = ∑(xi - μ)2/n, där μ är medelvärdet för sekvensen. Värdet σ kallas standardavvikelse, och σ2 kallas varians.
Typvärde, median och kvartiler
Ibland representerar medelvärdet inte tillräckligt väl det "typiska" värdet för data. Till exempel, när det finns några extrema värden som är helt utanför intervallet, kan de påverka medelvärdet. Ett annat bra mått är median, ett värde sådant att hälften av datapunkterna är lägre än det, och den andra hälften är högre.
För att förstå fördelningen av data är det också användbart att prata om kvartiler:
- Första kvartilen, eller Q1, är ett värde sådant att 25% av data ligger under det
- Tredje kvartilen, eller Q3, är ett värde sådant att 75% av data ligger under det
Grafiskt kan vi representera förhållandet mellan median och kvartiler i ett diagram som kallas låddiagram:

Här beräknar vi också interkvartilavstånd IQR=Q3-Q1, och så kallade uteliggare - värden som ligger utanför gränserna [Q1-1.5IQR,Q3+1.5IQR].
För en ändlig fördelning som innehåller ett litet antal möjliga värden är ett bra "typiskt" värde det som förekommer oftast, vilket kallas typvärde. Det används ofta för kategoriska data, såsom färger. Tänk på en situation där vi har två grupper av människor - några som starkt föredrar rött, och andra som föredrar blått. Om vi kodar färger med siffror, skulle medelvärdet för en favoritfärg ligga någonstans i det orange-gröna spektrumet, vilket inte indikerar den faktiska preferensen för någon av grupperna. Däremot skulle typvärdet vara antingen en av färgerna, eller båda färgerna, om antalet personer som röstar på dem är lika (i detta fall kallar vi stickprovet multimodalt).
Data från verkligheten
När vi analyserar data från verkligheten är de ofta inte slumpmässiga variabler i den meningen att vi inte utför experiment med okänt resultat. Till exempel, tänk på ett lag av basebollspelare och deras kroppsliga data, såsom längd, vikt och ålder. Dessa siffror är inte exakt slumpmässiga, men vi kan ändå tillämpa samma matematiska begrepp. Till exempel kan en sekvens av människors vikter betraktas som en sekvens av värden dragna från en slumpmässig variabel. Nedan är sekvensen av vikter för faktiska basebollspelare från Major League Baseball, hämtad från denna dataset (för din bekvämlighet visas endast de första 20 värdena):
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
Notera: För att se ett exempel på hur man arbetar med denna dataset, titta på den medföljande notebooken. Det finns också ett antal utmaningar genom hela lektionen, och du kan slutföra dem genom att lägga till lite kod i den notebooken. Om du inte är säker på hur man arbetar med data, oroa dig inte - vi kommer tillbaka till att arbeta med data med Python senare. Om du inte vet hur man kör kod i Jupyter Notebook, titta på denna artikel.
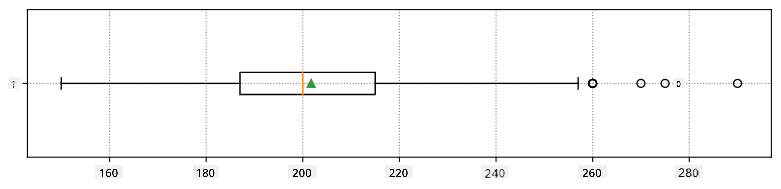
Här är låddiagrammet som visar medelvärde, median och kvartiler för våra data:
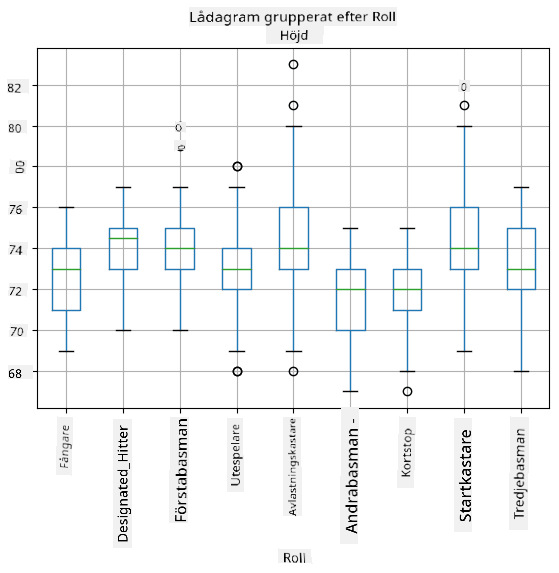
Eftersom våra data innehåller information om olika spelares roller, kan vi också göra ett låddiagram per roll - det låter oss få en uppfattning om hur parametrarnas värden skiljer sig mellan roller. Den här gången tittar vi på längd:
Detta diagram antyder att, i genomsnitt, är längden på första basmän högre än längden på andra basmän. Senare i denna lektion kommer vi att lära oss hur vi kan testa denna hypotes mer formellt och hur vi kan visa att våra data är statistiskt signifikanta för att bevisa detta.
När vi arbetar med data från verkligheten antar vi att alla datapunkter är stickprov dragna från någon sannolikhetsfördelning. Detta antagande gör det möjligt för oss att tillämpa maskininlärningstekniker och bygga fungerande prediktiva modeller.
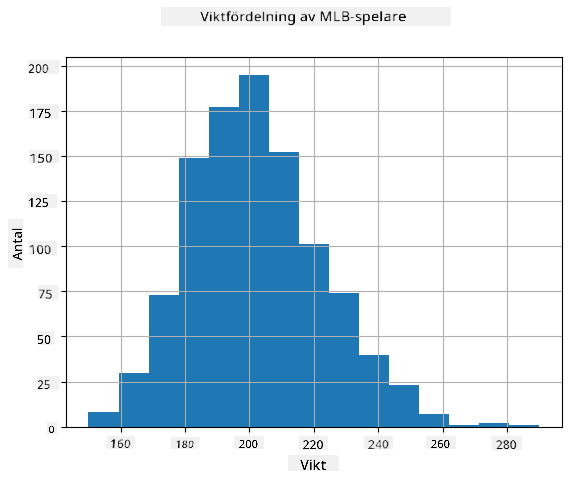
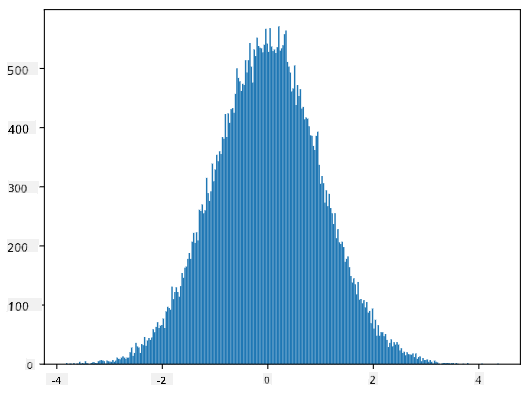
För att se hur fördelningen av våra data ser ut kan vi rita ett diagram som kallas histogram. X-axeln innehåller ett antal olika viktintervall (så kallade bins), och Y-axeln visar antalet gånger vårt stickprov av slumpmässiga variabler hamnade inom ett givet intervall.
Från detta histogram kan du se att alla värden är centrerade runt ett visst medelvärde, och ju längre vi går från det medelvärdet - desto färre vikter av det värdet förekommer. Det vill säga, det är mycket osannolikt att vikten på en basebollspelare skulle skilja sig mycket från medelvikten. Variansen i vikterna visar i vilken utsträckning vikterna sannolikt skiljer sig från medelvärdet.
Om vi tar vikter från andra människor, inte från basebolligan, är det troligt att fördelningen är annorlunda. Formen på fördelningen kommer dock att vara densamma, men medelvärdet och variansen skulle förändras. Så, om vi tränar vår modell på basebollspelare, är det troligt att den ger felaktiga resultat när den tillämpas på universitetsstudenter, eftersom den underliggande fördelningen är annorlunda.
Normalfördelning
Fördelningen av vikter som vi har sett ovan är mycket typisk, och många mätningar från verkligheten följer samma typ av fördelning, men med olika medelvärden och varians. Denna fördelning kallas normalfördelning, och den spelar en mycket viktig roll inom statistiken.
Att använda normalfördelning är ett korrekt sätt att generera slumpmässiga vikter för potentiella basebollspelare. När vi väl känner till medelvikten mean och standardavvikelsen std, kan vi generera 1000 viktstickprov på följande sätt:
samples = np.random.normal(mean,std,1000)
Om vi ritar histogrammet för de genererade stickproven kommer vi att se en bild mycket lik den som visas ovan. Och om vi ökar antalet stickprov och antalet bins, kan vi generera en bild av en normalfördelning som är närmare idealet:
Normalfördelning med medelvärde=0 och std.avvikelse=1
Konfidensintervall
När vi pratar om vikter på basebollspelare antar vi att det finns en viss slumpmässig variabel W som motsvarar den ideala sannolikhetsfördelningen av vikter för alla basebollspelare (den så kallade populationen). Vår sekvens av vikter motsvarar ett delmängd av alla basebollspelare som vi kallar stickprov. En intressant fråga är, kan vi känna till parametrarna för fördelningen av W, det vill säga medelvärdet och variansen för populationen?
Det enklaste svaret skulle vara att beräkna medelvärdet och variansen för vårt stickprov. Det kan dock hända att vårt slumpmässiga stickprov inte exakt representerar hela populationen. Därför är det meningsfullt att prata om konfidensintervall.
Konfidensintervall är uppskattningen av det sanna medelvärdet för populationen givet vårt stickprov, vilket är korrekt med en viss sannolikhet (eller konfidensnivå).
Anta att vi har ett stickprov X...
1, ..., Xn från vår fördelning. Varje gång vi drar ett stickprov från vår fördelning får vi ett annat medelvärde μ. Därför kan μ betraktas som en slumpvariabel. Ett konfidensintervall med konfidens p är ett par värden (Lp,Rp), sådana att P(Lp≤μ≤Rp) = p, det vill säga sannolikheten att det uppmätta medelvärdet ligger inom intervallet är lika med p.
Det går utöver vår korta introduktion att i detalj diskutera hur dessa konfidensintervall beräknas. Mer information finns på Wikipedia. Kort sagt definierar vi fördelningen av det beräknade stickprovsmedelvärdet i förhållande till populationens sanna medelvärde, vilket kallas studentfördelning.
Intressant fakta: Studentfördelningen är uppkallad efter matematikern William Sealy Gosset, som publicerade sin artikel under pseudonymen "Student". Han arbetade på Guinness bryggeri, och enligt en version ville hans arbetsgivare inte att allmänheten skulle veta att de använde statistiska tester för att bestämma kvaliteten på råvarorna.
Om vi vill uppskatta populationens medelvärde μ med konfidens p, behöver vi ta (1-p)/2:e percentilen av en studentfördelning A, som antingen kan hämtas från tabeller eller beräknas med inbyggda funktioner i statistisk programvara (t.ex. Python, R, etc.). Då ges intervallet för μ av X±A*D/√n, där X är det erhållna medelvärdet av stickprovet och D är standardavvikelsen.
Notera: Vi utelämnar också diskussionen om ett viktigt begrepp, frihetsgrader, som är relevant för studentfördelningen. Du kan hänvisa till mer kompletta böcker om statistik för att förstå detta begrepp djupare.
Ett exempel på beräkning av konfidensintervall för vikter och längder ges i medföljande anteckningsbok.
| p | Viktmedelvärde |
|---|---|
| 0.85 | 201.73±0.94 |
| 0.90 | 201.73±1.08 |
| 0.95 | 201.73±1.28 |
Observera att ju högre konfidenssannolikheten är, desto bredare är konfidensintervallet.
Hypotesprövning
I vår dataset med basebollspelare finns olika spelarroller, som kan sammanfattas nedan (se medföljande anteckningsbok för att se hur denna tabell kan beräknas):
| Roll | Längd | Vikt | Antal |
|---|---|---|---|
| Catcher | 72.723684 | 204.328947 | 76 |
| Designated_Hitter | 74.222222 | 220.888889 | 18 |
| First_Baseman | 74.000000 | 213.109091 | 55 |
| Outfielder | 73.010309 | 199.113402 | 194 |
| Relief_Pitcher | 74.374603 | 203.517460 | 315 |
| Second_Baseman | 71.362069 | 184.344828 | 58 |
| Shortstop | 71.903846 | 182.923077 | 52 |
| Starting_Pitcher | 74.719457 | 205.163636 | 221 |
| Third_Baseman | 73.044444 | 200.955556 | 45 |
Vi kan notera att medellängden för första basmän är högre än för andra basmän. Därför kan vi frestas att dra slutsatsen att första basmän är längre än andra basmän.
Detta påstående kallas en hypotes, eftersom vi inte vet om det faktiskt är sant eller inte.
Det är dock inte alltid uppenbart om vi kan dra denna slutsats. Från diskussionen ovan vet vi att varje medelvärde har ett tillhörande konfidensintervall, och därför kan denna skillnad bara vara ett statistiskt fel. Vi behöver ett mer formellt sätt att testa vår hypotes.
Låt oss beräkna konfidensintervall separat för längderna hos första och andra basmän:
| Konfidens | Första basmän | Andra basmän |
|---|---|---|
| 0.85 | 73.62..74.38 | 71.04..71.69 |
| 0.90 | 73.56..74.44 | 70.99..71.73 |
| 0.95 | 73.47..74.53 | 70.92..71.81 |
Vi kan se att under ingen konfidensnivå överlappar intervallen. Det bevisar vår hypotes att första basmän är längre än andra basmän.
Mer formellt är problemet vi löser att se om två sannolikhetsfördelningar är desamma, eller åtminstone har samma parametrar. Beroende på fördelningen behöver vi använda olika tester för detta. Om vi vet att våra fördelningar är normala kan vi tillämpa Student t-test.
I Student t-test beräknar vi den så kallade t-värdet, som indikerar skillnaden mellan medelvärdena med hänsyn till variansen. Det har visats att t-värdet följer studentfördelningen, vilket gör att vi kan få tröskelvärdet för en given konfidensnivå p (detta kan beräknas eller hittas i numeriska tabeller). Vi jämför sedan t-värdet med detta tröskelvärde för att godkänna eller förkasta hypotesen.
I Python kan vi använda SciPy-paketet, som inkluderar funktionen ttest_ind (förutom många andra användbara statistiska funktioner!). Den beräknar t-värdet åt oss och gör också den omvända uppslagningen av konfidens p-värde, så att vi bara kan titta på konfidensen för att dra slutsatsen.
Till exempel ger vår jämförelse mellan längderna hos första och andra basmän följande resultat:
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
T-value = 7.65
P-value: 9.137321189738925e-12
I vårt fall är p-värdet mycket lågt, vilket innebär att det finns starka bevis som stöder att första basmän är längre.
Det finns också olika andra typer av hypoteser som vi kanske vill testa, till exempel:
- Att bevisa att ett givet stickprov följer en viss fördelning. I vårt fall har vi antagit att längder är normalfördelade, men det behöver formell statistisk verifiering.
- Att bevisa att medelvärdet av ett stickprov motsvarar ett fördefinierat värde.
- Att jämföra medelvärdena för flera stickprov (t.ex. vad är skillnaden i lyckonivåer mellan olika åldersgrupper).
Lagen om stora tal och centrala gränsvärdessatsen
En av anledningarna till att normalfördelningen är så viktig är den så kallade centrala gränsvärdessatsen. Anta att vi har ett stort stickprov av oberoende N värden X1, ..., XN, tagna från en godtycklig fördelning med medelvärde μ och varians σ2. Då, för tillräckligt stort N (med andra ord, när N→∞), kommer medelvärdet ΣiXi att vara normalfördelat, med medelvärde μ och varians σ2/N.
Ett annat sätt att tolka den centrala gränsvärdessatsen är att säga att oavsett fördelning, när du beräknar medelvärdet av summan av slumpvariabelvärden, slutar du med en normalfördelning.
Från den centrala gränsvärdessatsen följer också att, när N→∞, blir sannolikheten att stickprovsmedelvärdet är lika med μ lika med 1. Detta är känt som lagen om stora tal.
Kovarians och korrelation
En av de saker som Data Science gör är att hitta relationer mellan data. Vi säger att två sekvenser korrelerar när de uppvisar liknande beteende samtidigt, det vill säga de antingen stiger/faller samtidigt, eller att en sekvens stiger när en annan faller och vice versa. Med andra ord verkar det finnas någon relation mellan två sekvenser.
Korrelation indikerar inte nödvändigtvis ett orsakssamband mellan två sekvenser; ibland kan båda variablerna bero på någon extern orsak, eller så kan det vara ren slump att de två sekvenserna korrelerar. Dock är stark matematisk korrelation en bra indikation på att två variabler på något sätt är kopplade.
Matematiskt är det huvudsakliga begreppet som visar relationen mellan två slumpvariabler kovarians, som beräknas så här: Cov(X,Y) = E[(X-E(X))(Y-E(Y))]. Vi beräknar avvikelsen för båda variablerna från deras medelvärden och sedan produkten av dessa avvikelser. Om båda variablerna avviker tillsammans kommer produkten alltid att vara ett positivt värde, vilket ger en positiv kovarians. Om båda variablerna avviker osynkroniserat (dvs. en faller under medelvärdet när en annan stiger över medelvärdet) får vi alltid negativa tal, vilket ger en negativ kovarians. Om avvikelserna är oberoende kommer de att summera till ungefär noll.
Kovariansens absoluta värde säger inte mycket om hur stor korrelationen är, eftersom det beror på storleken av de faktiska värdena. För att normalisera det kan vi dela kovariansen med standardavvikelsen för båda variablerna för att få korrelation. Det bra är att korrelation alltid ligger i intervallet [-1,1], där 1 indikerar stark positiv korrelation mellan värden, -1 - stark negativ korrelation, och 0 - ingen korrelation alls (variablerna är oberoende).
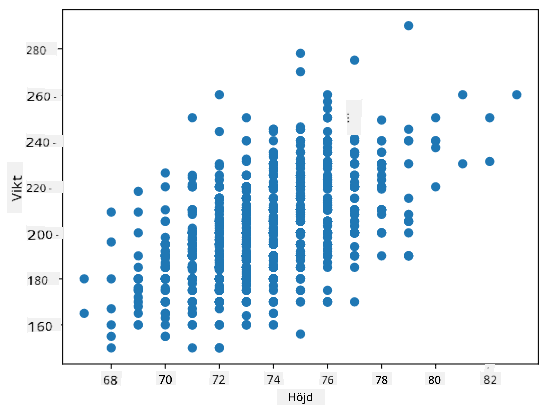
Exempel: Vi kan beräkna korrelationen mellan vikter och längder hos basebollspelare från datasetet som nämns ovan:
print(np.corrcoef(weights,heights))
Som resultat får vi korrelationsmatris som denna:
array([[1. , 0.52959196],
[0.52959196, 1. ]])
Korrelationsmatrisen C kan beräknas för valfritt antal inmatningssekvenser S1, ..., Sn. Värdet av Cij är korrelationen mellan Si och Sj, och diagonalelementen är alltid 1 (vilket också är självkorrelationen för Si).
I vårt fall indikerar värdet 0.53 att det finns viss korrelation mellan en persons vikt och längd. Vi kan också göra ett spridningsdiagram av ett värde mot det andra för att se relationen visuellt:
Fler exempel på korrelation och kovarians finns i medföljande anteckningsbok.
Slutsats
I denna sektion har vi lärt oss:
- grundläggande statistiska egenskaper hos data, såsom medelvärde, varians, typvärde och kvartiler
- olika fördelningar av slumpvariabler, inklusive normalfördelning
- hur man hittar korrelation mellan olika egenskaper
- hur man använder matematiska och statistiska metoder för att bevisa vissa hypoteser
- hur man beräknar konfidensintervall för en slumpvariabel givet ett stickprov
Även om detta definitivt inte är en uttömmande lista över ämnen inom sannolikhet och statistik, bör det vara tillräckligt för att ge dig en bra start i denna kurs.
🚀 Utmaning
Använd exempelkoden i anteckningsboken för att testa andra hypoteser:
- Första basmän är äldre än andra basmän
- Första basmän är längre än tredje basmän
- Shortstops är längre än andra basmän
Efterföreläsningsquiz
Granskning & Självstudier
Sannolikhet och statistik är ett så brett ämne att det förtjänar en egen kurs. Om du är intresserad av att fördjupa dig i teorin kan du fortsätta läsa några av följande böcker:
- Carlos Fernandez-Granda från New York University har utmärkta föreläsningsanteckningar Probability and Statistics for Data Science (tillgängliga online)
- Peter och Andrew Bruce. Practical Statistics for Data Scientists. [exempelkod i R].
- James D. Miller. Statistics for Data Science [exempelkod i R]
Uppgift
Krediter
Denna lektion har skapats med ♥️ av Dmitry Soshnikov
Ansvarsfriskrivning:
Detta dokument har översatts med hjälp av AI-översättningstjänsten Co-op Translator. Även om vi strävar efter noggrannhet, bör det noteras att automatiska översättningar kan innehålla fel eller inexaktheter. Det ursprungliga dokumentet på dess originalspråk bör betraktas som den auktoritativa källan. För kritisk information rekommenderas professionell mänsklig översättning. Vi ansvarar inte för eventuella missförstånd eller feltolkningar som uppstår vid användning av denna översättning.