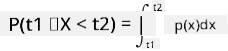|
|
2 weeks ago | |
|---|---|---|
| .. | ||
| solution | 2 weeks ago | |
| README.md | 2 weeks ago | |
| assignment.ipynb | 2 weeks ago | |
| assignment.md | 4 weeks ago | |
| notebook.ipynb | 2 weeks ago | |
README.md
O scurtă introducere în statistică și probabilitate
 |
|---|
| Statistică și Probabilitate - Sketchnote de @nitya |
Teoria statisticii și probabilității sunt două domenii strâns legate ale matematicii, extrem de relevante pentru știința datelor. Este posibil să lucrăm cu date fără o cunoaștere profundă a matematicii, dar este totuși mai bine să știm cel puțin câteva concepte de bază. Aici vom prezenta o scurtă introducere care te va ajuta să începi.
Chestionar înainte de lecție
Probabilitate și variabile aleatoare
Probabilitatea este un număr între 0 și 1 care exprimă cât de probabil este un eveniment. Este definită ca numărul de rezultate pozitive (care duc la eveniment), împărțit la numărul total de rezultate, presupunând că toate rezultatele sunt la fel de probabile. De exemplu, când aruncăm un zar, probabilitatea de a obține un număr par este 3/6 = 0.5.
Când vorbim despre evenimente, folosim variabile aleatoare. De exemplu, variabila aleatoare care reprezintă numărul obținut la aruncarea unui zar ar lua valori de la 1 la 6. Setul de numere de la 1 la 6 se numește spațiu de probă. Putem vorbi despre probabilitatea ca o variabilă aleatoare să ia o anumită valoare, de exemplu P(X=3)=1/6.
Variabila aleatoare din exemplul anterior se numește discretă, deoarece are un spațiu de probă numărabil, adică există valori separate care pot fi enumerate. Există cazuri în care spațiul de probă este un interval de numere reale sau întregul set de numere reale. Astfel de variabile se numesc continue. Un exemplu bun este timpul de sosire al autobuzului.
Distribuția probabilității
În cazul variabilelor aleatoare discrete, este ușor să descriem probabilitatea fiecărui eveniment printr-o funcție P(X). Pentru fiecare valoare s din spațiul de probă S, aceasta va da un număr între 0 și 1, astfel încât suma tuturor valorilor P(X=s) pentru toate evenimentele să fie 1.
Cea mai cunoscută distribuție discretă este distribuția uniformă, în care există un spațiu de probă cu N elemente, cu o probabilitate egală de 1/N pentru fiecare dintre ele.
Este mai dificil să descriem distribuția probabilității unei variabile continue, cu valori extrase dintr-un interval [a,b] sau întregul set de numere reale ℝ. Să luăm cazul timpului de sosire al autobuzului. De fapt, pentru fiecare moment exact de sosire t, probabilitatea ca autobuzul să sosească exact la acel moment este 0!
Acum știi că evenimentele cu probabilitate 0 se întâmplă, și foarte des! Cel puțin de fiecare dată când sosește autobuzul!
Putem vorbi doar despre probabilitatea ca o variabilă să se încadreze într-un anumit interval de valori, de exemplu P(t1≤X<t2). În acest caz, distribuția probabilității este descrisă printr-o funcție de densitate a probabilității p(x), astfel încât
Un analog continuu al distribuției uniforme se numește uniform continuu, care este definit pe un interval finit. Probabilitatea ca valoarea X să se încadreze într-un interval de lungime l este proporțională cu l și crește până la 1.
O altă distribuție importantă este distribuția normală, despre care vom vorbi mai detaliat mai jos.
Media, varianța și abaterea standard
Să presupunem că extragem o secvență de n probe ale unei variabile aleatoare X: x1, x2, ..., xn. Putem defini media (sau media aritmetică) a secvenței în mod tradițional ca (x1+x2+xn)/n. Pe măsură ce creștem dimensiunea probei (adică luăm limita cu n→∞), vom obține media (numită și așteptare) distribuției. Vom nota așteptarea cu E(x).
Se poate demonstra că pentru orice distribuție discretă cu valori {x1, x2, ..., xN} și probabilități corespunzătoare p1, p2, ..., pN, așteptarea ar fi egală cu E(X)=x1p1+x2p2+...+xNpN.
Pentru a identifica cât de mult sunt răspândite valorile, putem calcula varianța σ2 = ∑(xi - μ)2/n, unde μ este media secvenței. Valoarea σ se numește abatere standard, iar σ2 se numește varianță.
Mod, mediană și quartile
Uneori, media nu reprezintă adecvat valoarea "tipică" pentru date. De exemplu, când există câteva valori extreme care sunt complet în afara intervalului, acestea pot afecta media. O altă indicație bună este mediana, o valoare astfel încât jumătate dintre punctele de date sunt mai mici decât aceasta, iar cealaltă jumătate - mai mari.
Pentru a ne ajuta să înțelegem distribuția datelor, este util să vorbim despre quartile:
- Primul quartil, sau Q1, este o valoare astfel încât 25% din date sunt sub aceasta
- Al treilea quartil, sau Q3, este o valoare astfel încât 75% din date sunt sub aceasta
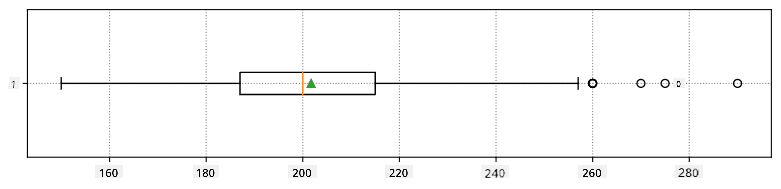
Grafic, putem reprezenta relația dintre mediană și quartile într-un diagramă numită box plot:

Aici calculăm și intervalul inter-quartil IQR=Q3-Q1 și așa-numitele valori extreme - valori care se află în afara limitelor [Q1-1.5IQR,Q3+1.5IQR].
Pentru o distribuție finită care conține un număr mic de valori posibile, o valoare "tipică" bună este cea care apare cel mai frecvent, numită mod. Este adesea aplicată datelor categorice, cum ar fi culorile. Să luăm o situație în care avem două grupuri de oameni - unii care preferă puternic roșu și alții care preferă albastru. Dacă codificăm culorile prin numere, valoarea medie pentru culoarea preferată ar fi undeva în spectrul portocaliu-verde, ceea ce nu indică preferința reală a niciunui grup. Totuși, modul ar fi fie una dintre culori, fie ambele culori, dacă numărul de persoane care votează pentru ele este egal (în acest caz, numim proba multimodală).
Date din lumea reală
Când analizăm date din viața reală, acestea nu sunt adesea variabile aleatoare în sensul că nu efectuăm experimente cu rezultat necunoscut. De exemplu, să luăm o echipă de jucători de baseball și datele lor corporale, cum ar fi înălțimea, greutatea și vârsta. Aceste numere nu sunt exact aleatoare, dar putem aplica aceleași concepte matematice. De exemplu, o secvență de greutăți ale oamenilor poate fi considerată o secvență de valori extrase dintr-o variabilă aleatoare. Mai jos este secvența greutăților jucătorilor de baseball din Major League Baseball, preluată din acest set de date (pentru comoditate, sunt afișate doar primele 20 de valori):
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
Notă: Pentru a vedea un exemplu de lucru cu acest set de date, consultă notebook-ul asociat. Există și o serie de provocări pe parcursul acestei lecții, pe care le poți completa adăugând cod în acel notebook. Dacă nu ești sigur cum să operezi cu datele, nu te îngrijora - vom reveni la lucrul cu date folosind Python mai târziu. Dacă nu știi cum să rulezi cod în Jupyter Notebook, consultă acest articol.
Iată box plot-ul care arată media, mediana și quartilele pentru datele noastre:
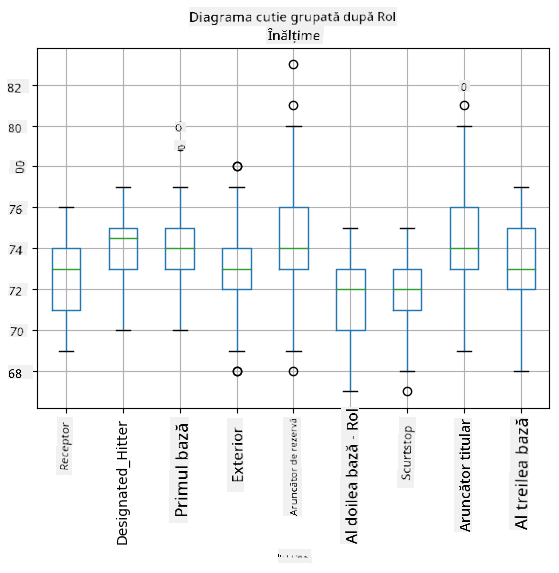
Deoarece datele noastre conțin informații despre diferite roluri ale jucătorilor, putem face și un box plot pe roluri - acest lucru ne va permite să înțelegem cum diferă valorile parametrilor între roluri. De această dată vom considera înălțimea:
Acest diagramă sugerează că, în medie, înălțimea jucătorilor de primă bază este mai mare decât înălțimea jucătorilor de a doua bază. Mai târziu în această lecție vom învăța cum putem testa această ipoteză mai formal și cum să demonstrăm că datele noastre sunt semnificative din punct de vedere statistic pentru a arăta acest lucru.
Când lucrăm cu date din lumea reală, presupunem că toate punctele de date sunt probe extrase dintr-o distribuție probabilistică. Această presupunere ne permite să aplicăm tehnici de învățare automată și să construim modele predictive funcționale.
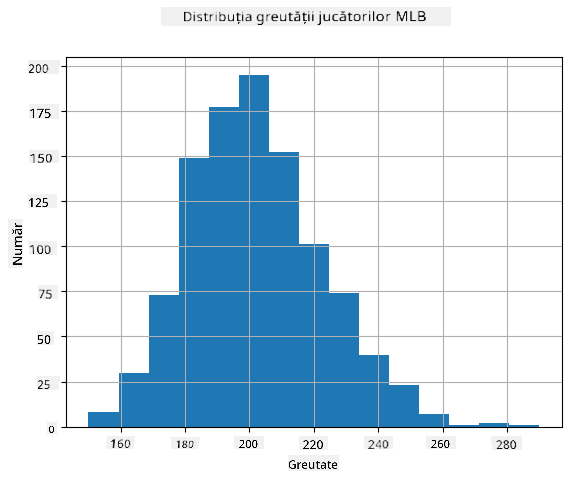
Pentru a vedea ce distribuție au datele noastre, putem trasa un grafic numit histogramă. Axa X ar conține un număr de intervale de greutate diferite (așa-numitele bin-uri), iar axa verticală ar arăta numărul de ori când proba variabilei aleatoare a fost în acel interval.
Din această histogramă poți vedea că toate valorile sunt centrate în jurul unei anumite greutăți medii, iar cu cât ne îndepărtăm de acea greutate - cu atât mai puține greutăți de acea valoare sunt întâlnite. Adică, este foarte improbabil ca greutatea unui jucător de baseball să fie foarte diferită de greutatea medie. Varianța greutăților arată măsura în care greutățile sunt susceptibile să difere de medie.
Dacă luăm greutățile altor persoane, nu din liga de baseball, distribuția este probabil să fie diferită. Totuși, forma distribuției va fi aceeași, dar media și varianța ar fi diferite. Deci, dacă antrenăm modelul nostru pe jucători de baseball, este probabil să dea rezultate greșite când este aplicat studenților unei universități, deoarece distribuția de bază este diferită.
Distribuția normală
Distribuția greutăților pe care am văzut-o mai sus este foarte tipică, iar multe măsurători din lumea reală urmează același tip de distribuție, dar cu medii și varianțe diferite. Această distribuție se numește distribuție normală și joacă un rol foarte important în statistică.
Utilizarea distribuției normale este o modalitate corectă de a genera greutăți aleatorii ale potențialilor jucători de baseball. Odată ce știm greutatea medie mean și abaterea standard std, putem genera 1000 de probe de greutate în următorul mod:
samples = np.random.normal(mean,std,1000)
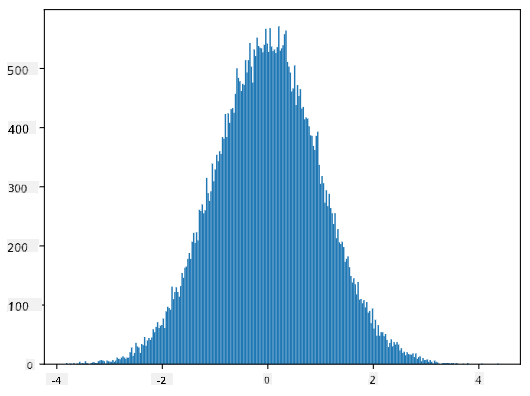
Dacă trasăm histograma probelor generate, vom vedea o imagine foarte similară cu cea prezentată mai sus. Și dacă mărim numărul de probe și numărul de bin-uri, putem genera o imagine a unei distribuții normale care este mai aproape de ideal:
Distribuție normală cu medie=0 și abatere standard=1
Intervalele de încredere
Când vorbim despre greutățile jucătorilor de baseball, presupunem că există o variabilă aleatoare W care corespunde distribuției ideale a greutăților tuturor jucătorilor de baseball (așa-numita populație). Secvența noastră de greutăți corespunde unui subset al tuturor jucătorilor de baseball pe care îl numim probă. O întrebare interesantă este: putem cunoaște parametrii distribuției lui W, adică media și varianța populației?
Cel mai simplu răspuns ar fi să calculăm media și varianța probei noastre. Totuși, s-ar putea întâmpla ca proba noastră aleatoare să nu reprezinte cu acuratețe întreaga populație. Astfel, are sens să vorbim despre intervalul de încredere.
Intervalul de încredere este estimarea mediei reale a populației dată proba noastră, care este precisă cu o anumită probabilitate (sau nivel de încredere).
Să presupunem că avem o probă X...
1, ..., Xn din distribuția noastră. De fiecare dată când extragem un eșantion din distribuție, vom obține o valoare medie diferită μ. Astfel, μ poate fi considerată o variabilă aleatoare. Un interval de încredere cu încredere p este o pereche de valori (Lp,Rp), astfel încât P(Lp≤μ≤Rp) = p, adică probabilitatea ca valoarea medie măsurată să se încadreze în interval este egală cu p.
Detaliile despre cum se calculează aceste intervale de încredere depășesc scopul acestei introduceri scurte. Mai multe detalii pot fi găsite pe Wikipedia. Pe scurt, definim distribuția mediei eșantionului calculat în raport cu media reală a populației, ceea ce se numește distribuția Student.
Fapt interesant: Distribuția Student poartă numele matematicianului William Sealy Gosset, care și-a publicat lucrarea sub pseudonimul "Student". El a lucrat la fabrica de bere Guinness și, conform unei versiuni, angajatorul său nu dorea ca publicul larg să știe că foloseau teste statistice pentru a determina calitatea materiilor prime.
Dacă dorim să estimăm media μ a populației noastre cu încredere p, trebuie să luăm (1-p)/2-th percentilă dintr-o distribuție Student A, care poate fi obținută fie din tabele, fie calculată folosind funcții încorporate ale unor programe statistice (de exemplu, Python, R etc.). Apoi, intervalul pentru μ ar fi dat de X±A*D/√n, unde X este media obținută a eșantionului, iar D este deviația standard.
Notă: De asemenea, omitem discuția despre un concept important al gradelor de libertate, care este relevant în raport cu distribuția Student. Puteți consulta cărți mai complete despre statistică pentru a înțelege mai bine acest concept.
Un exemplu de calcul al intervalului de încredere pentru greutăți și înălțimi este oferit în notebook-ul asociat.
| p | Media greutății |
|---|---|
| 0.85 | 201.73±0.94 |
| 0.90 | 201.73±1.08 |
| 0.95 | 201.73±1.28 |
Observați că, cu cât probabilitatea de încredere este mai mare, cu atât intervalul de încredere este mai larg.
Testarea ipotezelor
În setul nostru de date despre jucătorii de baseball, există diferite roluri ale jucătorilor, care pot fi rezumate mai jos (consultați notebook-ul asociat pentru a vedea cum se calculează acest tabel):
| Rol | Înălțime | Greutate | Număr |
|---|---|---|---|
| Catcher | 72.723684 | 204.328947 | 76 |
| Designated_Hitter | 74.222222 | 220.888889 | 18 |
| First_Baseman | 74.000000 | 213.109091 | 55 |
| Outfielder | 73.010309 | 199.113402 | 194 |
| Relief_Pitcher | 74.374603 | 203.517460 | 315 |
| Second_Baseman | 71.362069 | 184.344828 | 58 |
| Shortstop | 71.903846 | 182.923077 | 52 |
| Starting_Pitcher | 74.719457 | 205.163636 | 221 |
| Third_Baseman | 73.044444 | 200.955556 | 45 |
Putem observa că media înălțimilor pentru first basemen este mai mare decât cea pentru second basemen. Astfel, am putea fi tentați să concluzionăm că first basemen sunt mai înalți decât second basemen.
Această afirmație se numește o ipoteză, deoarece nu știm dacă acest fapt este cu adevărat adevărat sau nu.
Totuși, nu este întotdeauna evident dacă putem face această concluzie. Din discuția de mai sus știm că fiecare medie are un interval de încredere asociat, iar această diferență poate fi doar o eroare statistică. Avem nevoie de o metodă mai formală pentru a testa ipoteza noastră.
Să calculăm intervalele de încredere separat pentru înălțimile first și second basemen:
| Încredere | First Basemen | Second Basemen |
|---|---|---|
| 0.85 | 73.62..74.38 | 71.04..71.69 |
| 0.90 | 73.56..74.44 | 70.99..71.73 |
| 0.95 | 73.47..74.53 | 70.92..71.81 |
Putem observa că, pentru niciun nivel de încredere, intervalele nu se suprapun. Acest lucru dovedește ipoteza noastră că first basemen sunt mai înalți decât second basemen.
Mai formal, problema pe care o rezolvăm este să vedem dacă două distribuții de probabilitate sunt identice, sau cel puțin au aceiași parametri. În funcție de distribuție, trebuie să folosim teste diferite pentru aceasta. Dacă știm că distribuțiile noastre sunt normale, putem aplica Student t-test.
În Student t-test, calculăm așa-numitul t-value, care indică diferența dintre medii, luând în considerare variația. S-a demonstrat că t-value urmează distribuția Student, ceea ce ne permite să obținem valoarea prag pentru un nivel de încredere dat p (aceasta poate fi calculată sau găsită în tabele numerice). Comparăm apoi t-value cu acest prag pentru a aproba sau respinge ipoteza.
În Python, putem folosi pachetul SciPy, care include funcția ttest_ind (pe lângă multe alte funcții statistice utile!). Aceasta calculează t-value pentru noi și, de asemenea, face căutarea inversă a valorii p de încredere, astfel încât să putem analiza direct încrederea pentru a trage concluzii.
De exemplu, comparația noastră între înălțimile first și second basemen ne oferă următoarele rezultate:
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
T-value = 7.65
P-value: 9.137321189738925e-12
În cazul nostru, valoarea p este foarte mică, ceea ce înseamnă că există dovezi puternice care susțin că first basemen sunt mai înalți.
Există și alte tipuri de ipoteze pe care am putea dori să le testăm, de exemplu:
- Să demonstrăm că un eșantion dat urmează o anumită distribuție. În cazul nostru, am presupus că înălțimile sunt distribuite normal, dar acest lucru necesită o verificare statistică formală.
- Să demonstrăm că valoarea medie a unui eșantion corespunde unei valori predefinite.
- Să comparăm mediile mai multor eșantioane (de exemplu, care este diferența în nivelurile de fericire între diferite grupe de vârstă).
Legea numerelor mari și teorema limită centrală
Unul dintre motivele pentru care distribuția normală este atât de importantă este așa-numita teoremă limită centrală. Să presupunem că avem un eșantion mare de N valori independente X1, ..., XN, eșantionate din orice distribuție cu media μ și variația σ2. Atunci, pentru N suficient de mare (cu alte cuvinte, când N→∞), media ΣiXi va fi distribuită normal, cu media μ și variația σ2/N.
O altă modalitate de a interpreta teorema limită centrală este să spunem că, indiferent de distribuție, atunci când calculați media unei sume de valori aleatorii, ajungeți la o distribuție normală.
Din teorema limită centrală rezultă, de asemenea, că, atunci când N→∞, probabilitatea ca media eșantionului să fie egală cu μ devine 1. Aceasta este cunoscută sub numele de legea numerelor mari.
Covarianța și corelația
Unul dintre lucrurile pe care le face știința datelor este să găsească relații între date. Spunem că două secvențe corelează atunci când prezintă un comportament similar în același timp, adică fie cresc/scad simultan, fie o secvență crește când cealaltă scade și invers. Cu alte cuvinte, pare să existe o relație între cele două secvențe.
Corelația nu indică neapărat o relație cauzală între două secvențe; uneori ambele variabile pot depinde de o cauză externă sau poate fi pur întâmplător că cele două secvențe corelează. Totuși, o corelație matematică puternică este un indiciu bun că cele două variabile sunt cumva conectate.
Matematic, conceptul principal care arată relația dintre două variabile aleatoare este covarianța, care se calculează astfel: Cov(X,Y) = E[(X-E(X))(Y-E(Y))]. Calculăm deviația ambelor variabile față de valorile lor medii, apoi produsul acestor deviații. Dacă ambele variabile deviază împreună, produsul va fi întotdeauna o valoare pozitivă, care va adăuga la o covarianță pozitivă. Dacă ambele variabile deviază în afara sincronizării (adică una scade sub medie când cealaltă crește peste medie), vom obține întotdeauna numere negative, care vor adăuga la o covarianță negativă. Dacă deviațiile nu sunt dependente, ele vor adăuga aproximativ zero.
Valoarea absolută a covarianței nu ne spune prea multe despre cât de mare este corelația, deoarece depinde de magnitudinea valorilor reale. Pentru a o normaliza, putem împărți covarianța la deviația standard a ambelor variabile, pentru a obține corelația. Partea bună este că corelația este întotdeauna în intervalul [-1,1], unde 1 indică o corelație pozitivă puternică între valori, -1 - o corelație negativă puternică, iar 0 - nicio corelație (variabilele sunt independente).
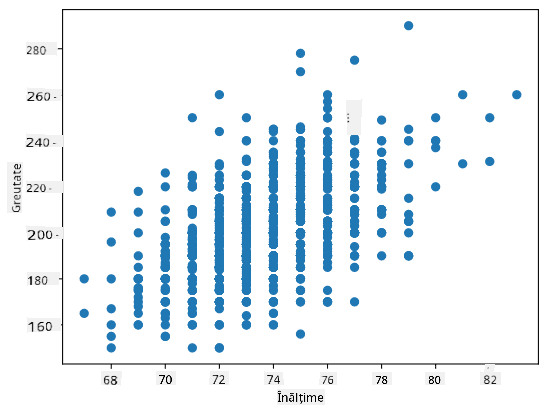
Exemplu: Putem calcula corelația între greutățile și înălțimile jucătorilor de baseball din setul de date menționat mai sus:
print(np.corrcoef(weights,heights))
Ca rezultat, obținem matricea de corelație astfel:
array([[1. , 0.52959196],
[0.52959196, 1. ]])
Matricea de corelație C poate fi calculată pentru orice număr de secvențe de intrare S1, ..., Sn. Valoarea Cij este corelația dintre Si și Sj, iar elementele diagonale sunt întotdeauna 1 (ceea ce reprezintă și autocorelația lui Si).
În cazul nostru, valoarea 0.53 indică faptul că există o anumită corelație între greutatea și înălțimea unei persoane. Putem, de asemenea, să realizăm un grafic scatter al unei valori în raport cu cealaltă pentru a vedea relația vizual:
Mai multe exemple de corelație și covarianță pot fi găsite în notebook-ul asociat.
Concluzie
În această secțiune, am învățat:
- proprietăți statistice de bază ale datelor, cum ar fi media, variația, moda și quartilele
- diferite distribuții ale variabilelor aleatoare, inclusiv distribuția normală
- cum să găsim corelația între diferite proprietăți
- cum să folosim aparatul matematic și statistic pentru a dovedi anumite ipoteze
- cum să calculăm intervale de încredere pentru o variabilă aleatoare pe baza unui eșantion de date
Deși aceasta nu este o listă exhaustivă a subiectelor care există în probabilitate și statistică, ar trebui să fie suficient pentru a vă oferi un început bun în acest curs.
🚀 Provocare
Folosiți codul exemplu din notebook pentru a testa alte ipoteze:
- First basemen sunt mai în vârstă decât second basemen
- First basemen sunt mai înalți decât third basemen
- Shortstops sunt mai înalți decât second basemen
Chestionar post-lectură
Recapitulare și studiu individual
Probabilitatea și statistica sunt subiecte atât de vaste încât merită un curs separat. Dacă sunteți interesați să aprofundați teoria, puteți continua să citiți unele dintre următoarele cărți:
- Carlos Fernandez-Granda de la Universitatea din New York are note excelente de curs Probability and Statistics for Data Science (disponibile online)
- Peter și Andrew Bruce. Practical Statistics for Data Scientists. [cod exemplu în R].
- James D. Miller. Statistics for Data Science [cod exemplu în R]
Temă
Credite
Această lecție a fost creată cu ♥️ de Dmitry Soshnikov
Declinarea responsabilității:
Acest document a fost tradus folosind serviciul de traducere AI Co-op Translator. Deși depunem eforturi pentru a asigura acuratețea, vă rugăm să aveți în vedere că traducerile automate pot conține erori sau inexactități. Documentul original în limba sa nativă ar trebui considerat sursa autoritară. Pentru informații critice, se recomandă traducerea profesională realizată de un specialist uman. Nu ne asumăm răspunderea pentru eventualele neînțelegeri sau interpretări greșite care pot apărea din utilizarea acestei traduceri.