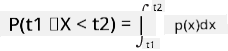|
|
2 weeks ago | |
|---|---|---|
| .. | ||
| solution | 2 weeks ago | |
| README.md | 2 weeks ago | |
| assignment.ipynb | 2 weeks ago | |
| assignment.md | 4 weeks ago | |
| notebook.ipynb | 2 weeks ago | |
README.md
Uma Breve Introdução à Estatística e Probabilidade
 |
|---|
| Estatística e Probabilidade - Sketchnote por @nitya |
A Teoria da Estatística e Probabilidade são duas áreas altamente relacionadas da Matemática que têm grande relevância para a Ciência de Dados. É possível trabalhar com dados sem um conhecimento profundo de matemática, mas é sempre melhor conhecer pelo menos alguns conceitos básicos. Aqui apresentaremos uma breve introdução que o ajudará a começar.
Questionário pré-aula
Probabilidade e Variáveis Aleatórias
Probabilidade é um número entre 0 e 1 que expressa o quão provável é que um evento ocorra. É definida como o número de resultados positivos (que levam ao evento), dividido pelo número total de resultados, assumindo que todos os resultados são igualmente prováveis. Por exemplo, ao lançar um dado, a probabilidade de obter um número par é 3/6 = 0.5.
Quando falamos de eventos, usamos variáveis aleatórias. Por exemplo, a variável aleatória que representa o número obtido ao lançar um dado pode assumir valores de 1 a 6. O conjunto de números de 1 a 6 é chamado de espaço amostral. Podemos falar sobre a probabilidade de uma variável aleatória assumir um determinado valor, por exemplo, P(X=3)=1/6.
A variável aleatória no exemplo anterior é chamada de discreta, porque possui um espaço amostral contável, ou seja, há valores separados que podem ser enumerados. Existem casos em que o espaço amostral é um intervalo de números reais ou o conjunto completo de números reais. Essas variáveis são chamadas de contínuas. Um bom exemplo é o horário de chegada de um autocarro.
Distribuição de Probabilidade
No caso de variáveis aleatórias discretas, é fácil descrever a probabilidade de cada evento por uma função P(X). Para cada valor s do espaço amostral S, ela fornecerá um número entre 0 e 1, de forma que a soma de todos os valores de P(X=s) para todos os eventos seja igual a 1.
A distribuição discreta mais conhecida é a distribuição uniforme, na qual há um espaço amostral de N elementos, com probabilidade igual de 1/N para cada um deles.
É mais difícil descrever a distribuição de probabilidade de uma variável contínua, com valores retirados de algum intervalo [a,b], ou do conjunto completo de números reais ℝ. Considere o caso do horário de chegada de um autocarro. Na verdade, para cada horário exato de chegada t, a probabilidade de o autocarro chegar exatamente nesse horário é 0!
Agora sabe que eventos com probabilidade 0 acontecem, e com muita frequência! Pelo menos cada vez que o autocarro chega!
Só podemos falar sobre a probabilidade de uma variável cair em um determinado intervalo de valores, por exemplo, P(t1≤X<t2). Nesse caso, a distribuição de probabilidade é descrita por uma função densidade de probabilidade p(x), tal que
Um análogo contínuo da distribuição uniforme é chamado de uniforme contínua, que é definida em um intervalo finito. A probabilidade de que o valor X caia em um intervalo de comprimento l é proporcional a l, e aumenta até 1.
Outra distribuição importante é a distribuição normal, sobre a qual falaremos mais detalhadamente abaixo.
Média, Variância e Desvio Padrão
Suponha que retiramos uma sequência de n amostras de uma variável aleatória X: x1, x2, ..., xn. Podemos definir o valor médio (ou média aritmética) da sequência da maneira tradicional como (x1+x2+xn)/n. À medida que aumentamos o tamanho da amostra (ou seja, tomamos o limite com n→∞), obteremos a média (também chamada de expectativa) da distribuição. Denotaremos a expectativa por E(x).
Pode-se demonstrar que, para qualquer distribuição discreta com valores {x1, x2, ..., xN} e probabilidades correspondentes p1, p2, ..., pN, a expectativa será igual a E(X)=x1p1+x2p2+...+xNpN.
Para identificar o quão dispersos os valores estão, podemos calcular a variância σ2 = ∑(xi - μ)2/n, onde μ é a média da sequência. O valor σ é chamado de desvio padrão, e σ2 é chamado de variância.
Moda, Mediana e Quartis
Às vezes, a média não representa adequadamente o valor "típico" dos dados. Por exemplo, quando há alguns valores extremos completamente fora do intervalo, eles podem afetar a média. Outra boa indicação é a mediana, um valor tal que metade dos pontos de dados são menores que ele, e a outra metade - maiores.
Para nos ajudar a entender a distribuição dos dados, é útil falar sobre quartis:
- Primeiro quartil, ou Q1, é um valor tal que 25% dos dados estão abaixo dele
- Terceiro quartil, ou Q3, é um valor tal que 75% dos dados estão abaixo dele
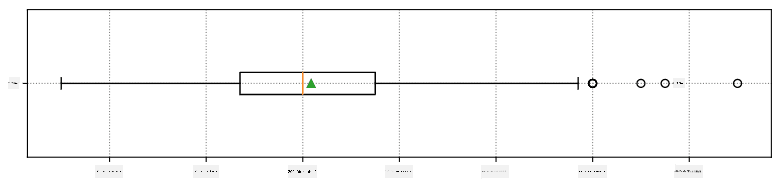
Graficamente, podemos representar a relação entre mediana e quartis em um diagrama chamado box plot:

Aqui também calculamos o intervalo interquartil IQR=Q3-Q1, e os chamados outliers - valores que estão fora dos limites [Q1-1.5IQR,Q3+1.5IQR].
Para uma distribuição finita que contém um pequeno número de valores possíveis, um bom valor "típico" é aquele que aparece com mais frequência, chamado de moda. É frequentemente aplicado a dados categóricos, como cores. Considere uma situação em que temos dois grupos de pessoas - algumas que preferem fortemente vermelho, e outras que preferem azul. Se codificarmos as cores por números, o valor médio para uma cor favorita estaria em algum lugar no espectro laranja-verde, o que não indica a preferência real de nenhum dos grupos. No entanto, a moda seria uma das cores ou ambas, se o número de pessoas que votaram por elas for igual (nesse caso, chamamos a amostra de multimodal).
Dados do Mundo Real
Quando analisamos dados da vida real, eles frequentemente não são variáveis aleatórias propriamente ditas, no sentido de que não realizamos experimentos com resultados desconhecidos. Por exemplo, considere uma equipa de jogadores de basebol e seus dados corporais, como altura, peso e idade. Esses números não são exatamente aleatórios, mas ainda podemos aplicar os mesmos conceitos matemáticos. Por exemplo, uma sequência de pesos de pessoas pode ser considerada uma sequência de valores retirados de alguma variável aleatória. Abaixo está a sequência de pesos de jogadores de basebol reais da Major League Baseball, retirada deste conjunto de dados (para sua conveniência, apenas os primeiros 20 valores são mostrados):
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
Nota: Para ver o exemplo de trabalho com este conjunto de dados, consulte o notebook associado. Há também vários desafios ao longo desta lição, e pode completá-los adicionando algum código a esse notebook. Se não souber como operar com dados, não se preocupe - voltaremos a trabalhar com dados usando Python mais tarde. Se não souber como executar código no Jupyter Notebook, consulte este artigo.
Aqui está o box plot mostrando média, mediana e quartis para os nossos dados:
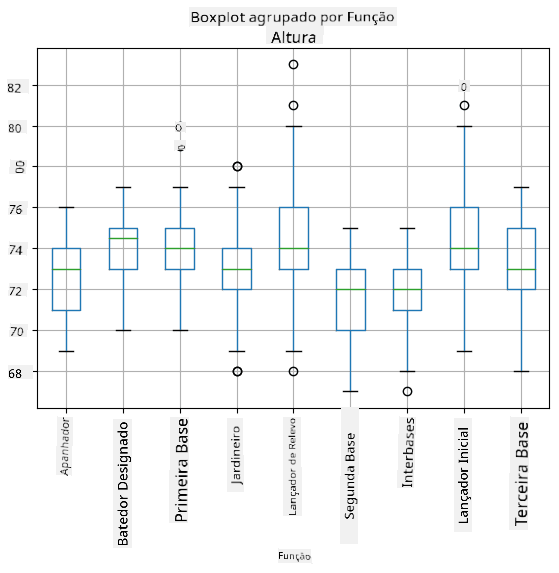
Como os nossos dados contêm informações sobre diferentes funções dos jogadores, também podemos fazer o box plot por função - isso permitirá que tenhamos uma ideia de como os valores dos parâmetros diferem entre as funções. Desta vez, consideraremos a altura:
Este diagrama sugere que, em média, a altura dos jogadores de primeira base é maior que a altura dos jogadores de segunda base. Mais tarde nesta lição, aprenderemos como podemos testar esta hipótese de forma mais formal e como demonstrar que os nossos dados são estatisticamente significativos para mostrar isso.
Ao trabalhar com dados do mundo real, assumimos que todos os pontos de dados são amostras retiradas de alguma distribuição de probabilidade. Essa suposição permite-nos aplicar técnicas de aprendizagem automática e construir modelos preditivos funcionais.
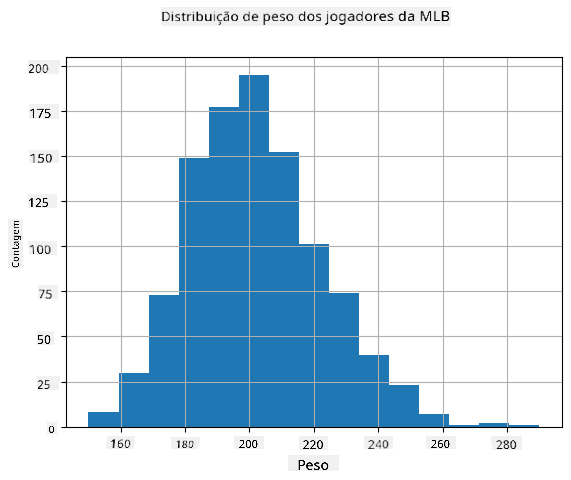
Para ver qual é a distribuição dos nossos dados, podemos traçar um gráfico chamado histograma. O eixo X conterá um número de diferentes intervalos de peso (os chamados bins), e o eixo vertical mostrará o número de vezes que a amostra da variável aleatória esteve dentro de um determinado intervalo.
A partir deste histograma, pode-se ver que todos os valores estão centrados em torno de um certo peso médio, e quanto mais nos afastamos desse peso - menos pesos desse valor são encontrados. Ou seja, é muito improvável que o peso de um jogador de basebol seja muito diferente do peso médio. A variância dos pesos mostra a extensão em que os pesos provavelmente diferem da média.
Se considerarmos os pesos de outras pessoas, não da liga de basebol, a distribuição provavelmente será diferente. No entanto, o formato da distribuição será o mesmo, mas a média e a variância mudariam. Assim, se treinarmos o nosso modelo com jogadores de basebol, é provável que ele produza resultados errados quando aplicado a estudantes de uma universidade, porque a distribuição subjacente é diferente.
Distribuição Normal
A distribuição de pesos que vimos acima é muito típica, e muitas medições do mundo real seguem o mesmo tipo de distribuição, mas com diferentes médias e variâncias. Esta distribuição é chamada de distribuição normal, e desempenha um papel muito importante na estatística.
Usar a distribuição normal é uma forma correta de gerar pesos aleatórios de potenciais jogadores de basebol. Uma vez que sabemos o peso médio mean e o desvio padrão std, podemos gerar 1000 amostras de peso da seguinte forma:
samples = np.random.normal(mean,std,1000)
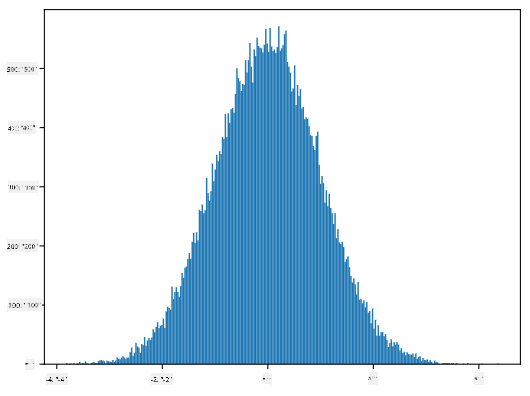
Se traçarmos o histograma das amostras geradas, veremos uma imagem muito semelhante à mostrada acima. E se aumentarmos o número de amostras e o número de bins, podemos gerar uma imagem de uma distribuição normal mais próxima do ideal:
Distribuição Normal com média=0 e desvio padrão=1
Intervalos de Confiança
Quando falamos sobre os pesos dos jogadores de basebol, assumimos que existe uma variável aleatória W que corresponde à distribuição de probabilidade ideal dos pesos de todos os jogadores de basebol (o chamado população). A nossa sequência de pesos corresponde a um subconjunto de todos os jogadores de basebol que chamamos de amostra. Uma questão interessante é: podemos conhecer os parâmetros da distribuição de W, ou seja, a média e a variância da população?
A resposta mais simples seria calcular a média e a variância da nossa amostra. No entanto, pode acontecer que a nossa amostra aleatória não represente com precisão a população completa. Assim, faz sentido falar sobre intervalo de confiança.
Intervalo de confiança é a estimativa da verdadeira média da população dada a nossa amostra, que é precisa com uma certa probabilidade (ou nível de confiança).
Suponha que temos uma amostra X
1, ..., Xn da nossa distribuição. Cada vez que retiramos uma amostra da nossa distribuição, acabamos com um valor médio diferente μ. Assim, μ pode ser considerado uma variável aleatória. Um intervalo de confiança com confiança p é um par de valores (Lp,Rp), tal que P(Lp≤μ≤Rp) = p, ou seja, a probabilidade de o valor médio medido estar dentro do intervalo é igual a p.
Vai além da nossa breve introdução discutir em detalhe como esses intervalos de confiança são calculados. Mais detalhes podem ser encontrados na Wikipedia. Em resumo, definimos a distribuição da média amostral calculada em relação à verdadeira média da população, que é chamada de distribuição de Student.
Fato interessante: A distribuição de Student foi nomeada em homenagem ao matemático William Sealy Gosset, que publicou seu artigo sob o pseudônimo "Student". Ele trabalhava na cervejaria Guinness e, segundo uma das versões, seu empregador não queria que o público soubesse que estavam a usar testes estatísticos para determinar a qualidade das matérias-primas.
Se quisermos estimar a média μ da nossa população com confiança p, precisamos tomar o (1-p)/2-th percentil de uma distribuição de Student A, que pode ser obtido em tabelas ou calculado usando algumas funções integradas de software estatístico (ex. Python, R, etc.). Então, o intervalo para μ seria dado por X±A*D/√n, onde X é a média obtida da amostra e D é o desvio padrão.
Nota: Também omitimos a discussão de um conceito importante de graus de liberdade, que é relevante em relação à distribuição de Student. Pode consultar livros mais completos sobre estatística para entender este conceito mais profundamente.
Um exemplo de cálculo de intervalo de confiança para pesos e alturas é dado nos notebooks associados.
| p | Média do peso |
|---|---|
| 0.85 | 201.73±0.94 |
| 0.90 | 201.73±1.08 |
| 0.95 | 201.73±1.28 |
Note que quanto maior a probabilidade de confiança, mais amplo é o intervalo de confiança.
Teste de Hipóteses
No nosso conjunto de dados de jogadores de baseball, existem diferentes funções de jogadores, que podem ser resumidas abaixo (veja o notebook associado para ver como esta tabela pode ser calculada):
| Função | Altura | Peso | Contagem |
|---|---|---|---|
| Catcher | 72.723684 | 204.328947 | 76 |
| Designated_Hitter | 74.222222 | 220.888889 | 18 |
| First_Baseman | 74.000000 | 213.109091 | 55 |
| Outfielder | 73.010309 | 199.113402 | 194 |
| Relief_Pitcher | 74.374603 | 203.517460 | 315 |
| Second_Baseman | 71.362069 | 184.344828 | 58 |
| Shortstop | 71.903846 | 182.923077 | 52 |
| Starting_Pitcher | 74.719457 | 205.163636 | 221 |
| Third_Baseman | 73.044444 | 200.955556 | 45 |
Podemos notar que as alturas médias dos jogadores de primeira base são maiores do que as dos jogadores de segunda base. Assim, podemos ser tentados a concluir que jogadores de primeira base são mais altos do que jogadores de segunda base.
Esta afirmação é chamada de hipótese, porque não sabemos se o fato é realmente verdadeiro ou não.
No entanto, nem sempre é óbvio se podemos fazer esta conclusão. Pela discussão acima, sabemos que cada média tem um intervalo de confiança associado e, portanto, esta diferença pode ser apenas um erro estatístico. Precisamos de uma forma mais formal de testar a nossa hipótese.
Vamos calcular intervalos de confiança separadamente para as alturas dos jogadores de primeira e segunda base:
| Confiança | Primeira Base | Segunda Base |
|---|---|---|
| 0.85 | 73.62..74.38 | 71.04..71.69 |
| 0.90 | 73.56..74.44 | 70.99..71.73 |
| 0.95 | 73.47..74.53 | 70.92..71.81 |
Podemos ver que, sob nenhuma confiança, os intervalos se sobrepõem. Isso prova a nossa hipótese de que jogadores de primeira base são mais altos do que jogadores de segunda base.
Mais formalmente, o problema que estamos a resolver é verificar se duas distribuições de probabilidade são iguais, ou pelo menos têm os mesmos parâmetros. Dependendo da distribuição, precisamos usar diferentes testes para isso. Se sabemos que as nossas distribuições são normais, podemos aplicar o teste t de Student.
No teste t de Student, calculamos o chamado valor t, que indica a diferença entre as médias, levando em conta a variância. É demonstrado que o valor t segue a distribuição de Student, o que nos permite obter o valor limite para um nível de confiança p (isto pode ser calculado ou consultado em tabelas numéricas). Depois comparamos o valor t com este limite para aprovar ou rejeitar a hipótese.
Em Python, podemos usar o pacote SciPy, que inclui a função ttest_ind (além de muitas outras funções estatísticas úteis!). Ela calcula o valor t para nós e também faz a consulta inversa do valor de confiança p, para que possamos apenas olhar para a confiança e tirar a conclusão.
Por exemplo, a nossa comparação entre as alturas dos jogadores de primeira e segunda base dá-nos os seguintes resultados:
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
T-value = 7.65
P-value: 9.137321189738925e-12
No nosso caso, o valor p é muito baixo, o que significa que há fortes evidências que suportam que jogadores de primeira base são mais altos.
Existem também outros tipos de hipóteses que podemos querer testar, por exemplo:
- Provar que uma amostra segue alguma distribuição. No nosso caso, assumimos que as alturas são distribuídas normalmente, mas isso precisa de verificação estatística formal.
- Provar que o valor médio de uma amostra corresponde a algum valor pré-definido.
- Comparar médias de várias amostras (ex. qual é a diferença nos níveis de felicidade entre diferentes faixas etárias).
Lei dos Grandes Números e Teorema do Limite Central
Uma das razões pela qual a distribuição normal é tão importante é o chamado teorema do limite central. Suponha que temos uma grande amostra de N valores independentes X1, ..., XN, amostrados de qualquer distribuição com média μ e variância σ2. Então, para N suficientemente grande (em outras palavras, quando N→∞), a média ΣiXi seria normalmente distribuída, com média μ e variância σ2/N.
Outra forma de interpretar o teorema do limite central é dizer que, independentemente da distribuição, quando calculamos a média de uma soma de valores de qualquer variável aleatória, acabamos com uma distribuição normal.
Do teorema do limite central também segue que, quando N→∞, a probabilidade de a média da amostra ser igual a μ torna-se 1. Isto é conhecido como a lei dos grandes números.
Covariância e Correlação
Uma das coisas que a Ciência de Dados faz é encontrar relações entre dados. Dizemos que duas sequências correlacionam quando exibem comportamentos semelhantes ao mesmo tempo, ou seja, elas sobem/descem simultaneamente, ou uma sequência sobe quando outra desce e vice-versa. Em outras palavras, parece haver alguma relação entre duas sequências.
Correlação não indica necessariamente uma relação causal entre duas sequências; às vezes ambas as variáveis podem depender de alguma causa externa, ou pode ser puramente por acaso que as duas sequências correlacionam. No entanto, uma correlação matemática forte é uma boa indicação de que duas variáveis estão de alguma forma conectadas.
Matematicamente, o principal conceito que mostra a relação entre duas variáveis aleatórias é a covariância, que é calculada assim: Cov(X,Y) = E[(X-E(X))(Y-E(Y))]. Calculamos o desvio de ambas as variáveis em relação aos seus valores médios e, em seguida, o produto desses desvios. Se ambas as variáveis se desviam juntas, o produto será sempre um valor positivo, que somará para uma covariância positiva. Se ambas as variáveis se desviam fora de sincronia (ou seja, uma cai abaixo da média quando outra sobe acima da média), sempre obteremos números negativos, que somarão para uma covariância negativa. Se os desvios não são dependentes, eles somarão aproximadamente zero.
O valor absoluto da covariância não nos diz muito sobre o quão grande é a correlação, porque depende da magnitude dos valores reais. Para normalizá-lo, podemos dividir a covariância pelo desvio padrão de ambas as variáveis, para obter a correlação. A vantagem é que a correlação está sempre no intervalo de [-1,1], onde 1 indica uma correlação positiva forte entre os valores, -1 - uma correlação negativa forte, e 0 - nenhuma correlação (variáveis independentes).
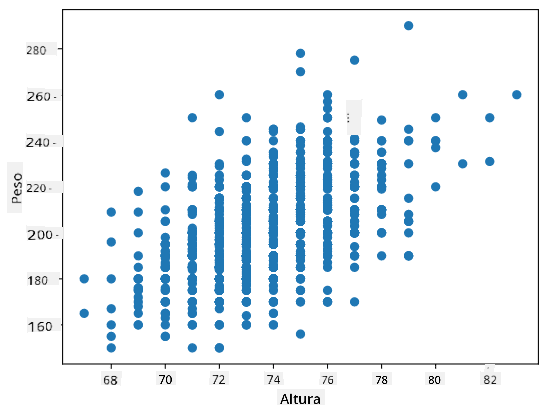
Exemplo: Podemos calcular a correlação entre pesos e alturas dos jogadores de baseball do conjunto de dados mencionado acima:
print(np.corrcoef(weights,heights))
Como resultado, obtemos uma matriz de correlação como esta:
array([[1. , 0.52959196],
[0.52959196, 1. ]])
A matriz de correlação C pode ser calculada para qualquer número de sequências de entrada S1, ..., Sn. O valor de Cij é a correlação entre Si e Sj, e os elementos diagonais são sempre 1 (que é também a autocorrelação de Si).
No nosso caso, o valor 0.53 indica que há alguma correlação entre o peso e a altura de uma pessoa. Podemos também fazer o gráfico de dispersão de um valor contra o outro para ver a relação visualmente:
Mais exemplos de correlação e covariância podem ser encontrados no notebook associado.
Conclusão
Nesta seção, aprendemos:
- propriedades estatísticas básicas dos dados, como média, variância, moda e quartis
- diferentes distribuições de variáveis aleatórias, incluindo a distribuição normal
- como encontrar correlação entre diferentes propriedades
- como usar um aparato sólido de matemática e estatística para provar algumas hipóteses
- como calcular intervalos de confiança para variáveis aleatórias dado um conjunto de dados
Embora esta não seja uma lista exaustiva de tópicos que existem dentro de probabilidade e estatística, deve ser suficiente para lhe dar um bom início neste curso.
🚀 Desafio
Use o código de exemplo no notebook para testar outras hipóteses:
- Jogadores de primeira base são mais velhos do que jogadores de segunda base
- Jogadores de primeira base são mais altos do que jogadores de terceira base
- Shortstops são mais altos do que jogadores de segunda base
Quiz pós-aula
Revisão e Autoestudo
Probabilidade e estatística é um tópico tão amplo que merece seu próprio curso. Se estiver interessado em aprofundar-se na teoria, pode continuar a ler alguns dos seguintes livros:
- Carlos Fernandez-Granda da Universidade de Nova York tem ótimos apontamentos Probability and Statistics for Data Science (disponível online)
- Peter e Andrew Bruce. Practical Statistics for Data Scientists. [código de exemplo em R].
- James D. Miller. Statistics for Data Science [código de exemplo em R]
Tarefa
Créditos
Esta lição foi criada com ♥️ por Dmitry Soshnikov
Aviso Legal:
Este documento foi traduzido utilizando o serviço de tradução por IA Co-op Translator. Embora nos esforcemos para garantir a precisão, é importante notar que traduções automáticas podem conter erros ou imprecisões. O documento original na sua língua nativa deve ser considerado a fonte autoritária. Para informações críticas, recomenda-se uma tradução profissional realizada por humanos. Não nos responsabilizamos por quaisquer mal-entendidos ou interpretações incorretas decorrentes da utilização desta tradução.