History

leestott b3d803186c 🌐 Update translations via Co-op Translator		4 weeks ago
..
README.md	🌐 Update translations via Co-op Translator	4 weeks ago
assignment.md	🌐 Update translations via Co-op Translator	4 weeks ago

README.md

การแสดงภาพการกระจายตัวของข้อมูล


การแสดงภาพการกระจายตัวของข้อมูล - สเก็ตช์โน้ตโดย @nitya

ในบทเรียนก่อนหน้านี้ คุณได้เรียนรู้ข้อเท็จจริงที่น่าสนใจเกี่ยวกับชุดข้อมูลเกี่ยวกับนกในรัฐมินนิโซตา คุณพบข้อมูลที่ผิดพลาดโดยการแสดงภาพค่าผิดปกติ และได้ดูความแตกต่างระหว่างหมวดหมู่นกตามความยาวสูงสุดของพวกมัน

แบบทดสอบก่อนเรียน

สำรวจชุดข้อมูลนก

อีกวิธีหนึ่งในการเจาะลึกข้อมูลคือการดูการกระจายตัวของข้อมูล หรือวิธีที่ข้อมูลถูกจัดเรียงตามแกนตัวอย่าง เช่น คุณอาจต้องการเรียนรู้เกี่ยวกับการกระจายตัวทั่วไปของความกว้างปีกสูงสุดหรือมวลร่างกายสูงสุดของนกในรัฐมินนิโซตาในชุดข้อมูลนี้

มาค้นหาข้อเท็จจริงบางอย่างเกี่ยวกับการกระจายตัวของข้อมูลในชุดข้อมูลนี้กัน ในไฟล์ notebook.ipynb ที่อยู่ในโฟลเดอร์บทเรียนนี้ ให้นำเข้า Pandas, Matplotlib และข้อมูลของคุณ:

import pandas as pd
import matplotlib.pyplot as plt
birds = pd.read_csv('../../data/birds.csv')
birds.head()

	ชื่อ	ชื่อวิทยาศาสตร์	หมวดหมู่	ลำดับ	วงศ์	สกุล	สถานะการอนุรักษ์	ความยาวต่ำสุด	ความยาวสูงสุด	มวลร่างกายต่ำสุด	มวลร่างกายสูงสุด	ความกว้างปีกต่ำสุด	ความกว้างปีกสูงสุด
0	เป็ดหวีดท้องดำ	Dendrocygna autumnalis	เป็ด/ห่าน/นกน้ำ	Anseriformes	Anatidae	Dendrocygna	LC	47	56	652	1020	76	94
1	เป็ดหวีดสีน้ำตาล	Dendrocygna bicolor	เป็ด/ห่าน/นกน้ำ	Anseriformes	Anatidae	Dendrocygna	LC	45	53	712	1050	85	93
2	ห่านหิมะ	Anser caerulescens	เป็ด/ห่าน/นกน้ำ	Anseriformes	Anatidae	Anser	LC	64	79	2050	4050	135	165
3	ห่านรอสส์	Anser rossii	เป็ด/ห่าน/นกน้ำ	Anseriformes	Anatidae	Anser	LC	57.3	64	1066	1567	113	116
4	ห่านหน้าขาวใหญ่	Anser albifrons	เป็ด/ห่าน/นกน้ำ	Anseriformes	Anatidae	Anser	LC	64	81	1930	3310	130	165

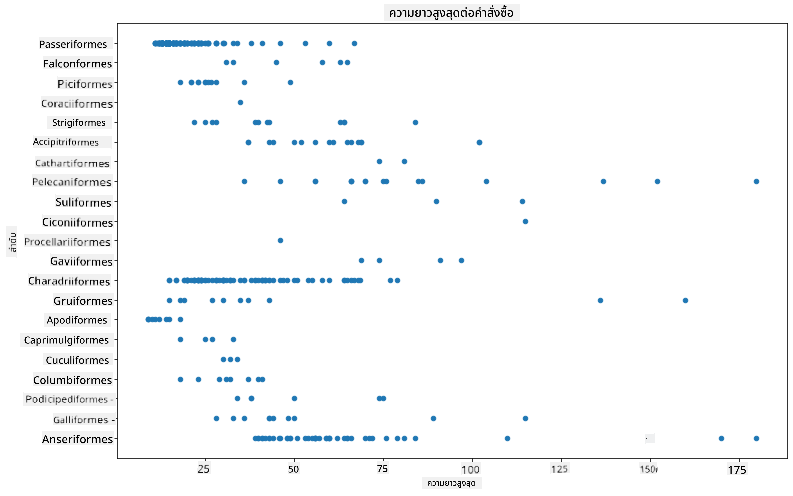
โดยทั่วไป คุณสามารถดูการกระจายตัวของข้อมูลได้อย่างรวดเร็วโดยใช้แผนภาพกระจาย (scatter plot) เช่นเดียวกับที่เราได้ทำในบทเรียนก่อนหน้านี้:

birds.plot(kind='scatter',x='MaxLength',y='Order',figsize=(12,8))

plt.title('Max Length per Order')
plt.ylabel('Order')
plt.xlabel('Max Length')

plt.show()

นี่เป็นภาพรวมของการกระจายตัวทั่วไปของความยาวร่างกายต่ออันดับของนก แต่ไม่ใช่วิธีที่เหมาะสมที่สุดในการแสดงการกระจายตัวที่แท้จริง งานนี้มักจะทำโดยการสร้างฮิสโตแกรม

การทำงานกับฮิสโตแกรม

Matplotlib มีวิธีที่ดีมากในการแสดงการกระจายตัวของข้อมูลโดยใช้ฮิสโตแกรม แผนภูมิประเภทนี้คล้ายกับแผนภูมิแท่งที่การกระจายตัวสามารถมองเห็นได้ผ่านการเพิ่มขึ้นและลดลงของแท่งข้อมูล ในการสร้างฮิสโตแกรม คุณต้องมีข้อมูลเชิงตัวเลข ในการสร้างฮิสโตแกรม คุณสามารถสร้างแผนภูมิที่กำหนดชนิดเป็น 'hist' สำหรับฮิสโตแกรม แผนภูมินี้แสดงการกระจายตัวของ MaxBodyMass สำหรับช่วงข้อมูลเชิงตัวเลขทั้งหมดในชุดข้อมูล โดยการแบ่งข้อมูลออกเป็นกลุ่มย่อย (bins) จะสามารถแสดงการกระจายตัวของค่าข้อมูลได้:

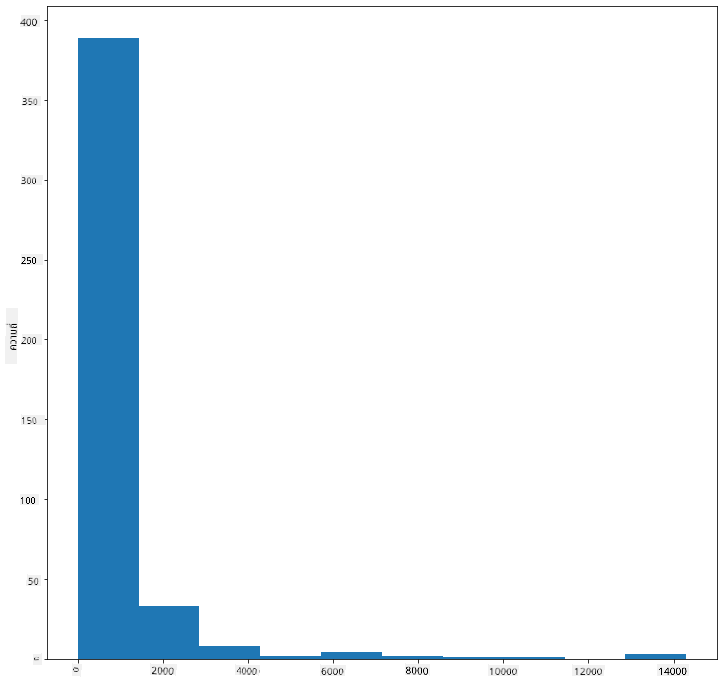
birds['MaxBodyMass'].plot(kind = 'hist', bins = 10, figsize = (12,12))
plt.show()

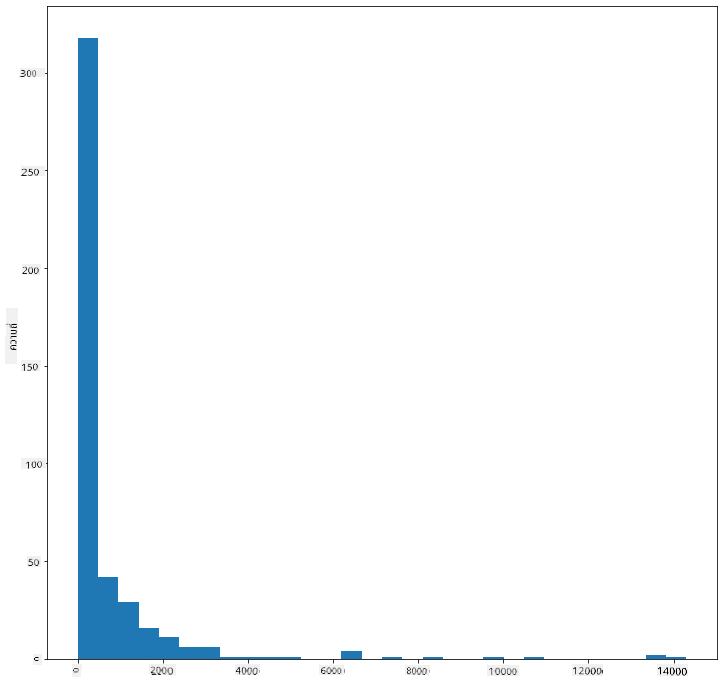
ดังที่คุณเห็น นกส่วนใหญ่ในชุดข้อมูลกว่า 400 ตัวนี้มีมวลร่างกายสูงสุดต่ำกว่า 2000 ลองเปลี่ยนพารามิเตอร์ bins เป็นค่าที่สูงขึ้น เช่น 30 เพื่อดูข้อมูลในรายละเอียดมากขึ้น:

birds['MaxBodyMass'].plot(kind = 'hist', bins = 30, figsize = (12,12))
plt.show()

แผนภูมินี้แสดงการกระจายตัวในลักษณะที่ละเอียดขึ้นเล็กน้อย คุณสามารถสร้างแผนภูมิที่ไม่เอียงไปทางซ้ายมากเกินไปได้โดยการเลือกข้อมูลเฉพาะในช่วงที่กำหนด:

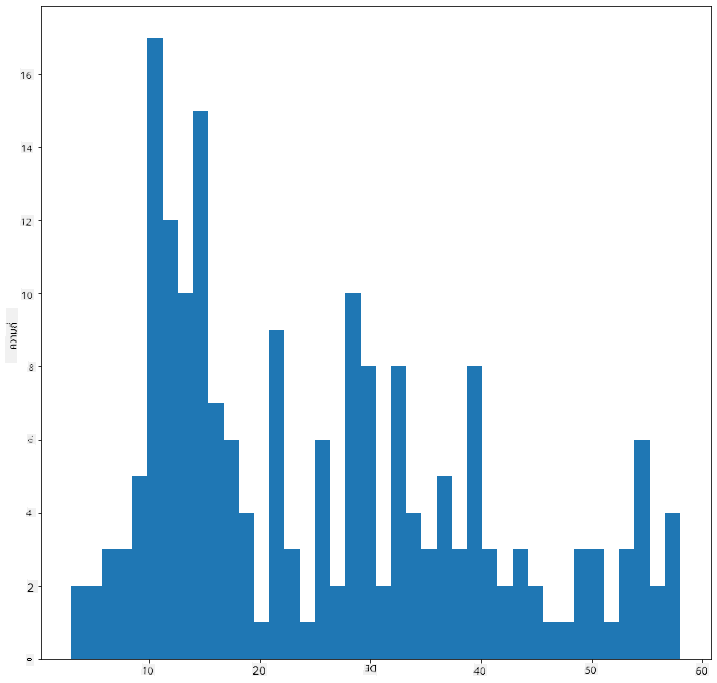
กรองข้อมูลของคุณเพื่อเลือกเฉพาะนกที่มีมวลร่างกายต่ำกว่า 60 และแสดง bins จำนวน 40:

filteredBirds = birds[(birds['MaxBodyMass'] > 1) & (birds['MaxBodyMass'] < 60)]      
filteredBirds['MaxBodyMass'].plot(kind = 'hist',bins = 40,figsize = (12,12))
plt.show()

✅ ลองใช้ตัวกรองและจุดข้อมูลอื่น ๆ เพื่อดูการกระจายตัวของข้อมูลทั้งหมด ลบตัวกรอง ['MaxBodyMass'] เพื่อแสดงการกระจายตัวที่มีการติดป้ายกำกับ

ฮิสโตแกรมยังมีการปรับปรุงสีและการติดป้ายกำกับที่น่าสนใจให้ลองใช้ด้วย:

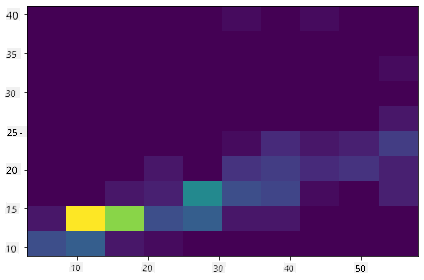
สร้างฮิสโตแกรม 2 มิติ เพื่อเปรียบเทียบความสัมพันธ์ระหว่างการกระจายตัวสองแบบ ลองเปรียบเทียบ MaxBodyMass กับ MaxLength Matplotlib มีวิธีในตัวเพื่อแสดงการบรรจบกันโดยใช้สีที่สว่างขึ้น:

x = filteredBirds['MaxBodyMass']
y = filteredBirds['MaxLength']

fig, ax = plt.subplots(tight_layout=True)
hist = ax.hist2d(x, y)

ดูเหมือนว่าจะมีความสัมพันธ์ที่คาดหวังระหว่างสององค์ประกอบนี้ตามแกนที่คาดไว้ โดยมีจุดบรรจบที่แข็งแกร่งจุดหนึ่ง:

ฮิสโตแกรมทำงานได้ดีโดยค่าเริ่มต้นสำหรับข้อมูลเชิงตัวเลข แล้วถ้าคุณต้องการดูการกระจายตัวตามข้อมูลข้อความล่ะ?

สำรวจชุดข้อมูลเพื่อดูการกระจายตัวโดยใช้ข้อมูลข้อความ

ชุดข้อมูลนี้ยังมีข้อมูลที่ดีเกี่ยวกับหมวดหมู่นก สกุล สปีชีส์ และวงศ์ รวมถึงสถานะการอนุรักษ์ มาสำรวจข้อมูลสถานะการอนุรักษ์นี้กัน การกระจายตัวของนกตามสถานะการอนุรักษ์เป็นอย่างไร?

✅ ในชุดข้อมูลนี้ มีการใช้ตัวย่อหลายตัวเพื่ออธิบายสถานะการอนุรักษ์ ตัวย่อเหล่านี้มาจาก IUCN Red List Categories ซึ่งเป็นองค์กรที่จัดทำรายการสถานะของสปีชีส์

CR: ใกล้สูญพันธุ์อย่างยิ่ง

EN: ใกล้สูญพันธุ์

EX: สูญพันธุ์

LC: ความกังวลน้อยที่สุด

NT: ใกล้ถูกคุกคาม

VU: มีแนวโน้มใกล้สูญพันธุ์

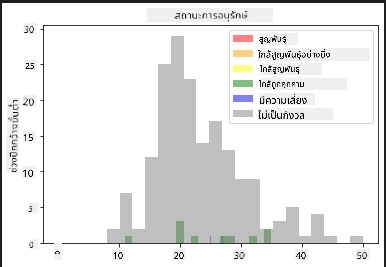
ค่าพวกนี้เป็นค่าข้อความ ดังนั้นคุณจะต้องทำการแปลงเพื่อสร้างฮิสโตแกรม โดยใช้ dataframe ที่กรองแล้ว แสดงสถานะการอนุรักษ์ควบคู่ไปกับความกว้างปีกขั้นต่ำ คุณเห็นอะไรบ้าง?

x1 = filteredBirds.loc[filteredBirds.ConservationStatus=='EX', 'MinWingspan']
x2 = filteredBirds.loc[filteredBirds.ConservationStatus=='CR', 'MinWingspan']
x3 = filteredBirds.loc[filteredBirds.ConservationStatus=='EN', 'MinWingspan']
x4 = filteredBirds.loc[filteredBirds.ConservationStatus=='NT', 'MinWingspan']
x5 = filteredBirds.loc[filteredBirds.ConservationStatus=='VU', 'MinWingspan']
x6 = filteredBirds.loc[filteredBirds.ConservationStatus=='LC', 'MinWingspan']

kwargs = dict(alpha=0.5, bins=20)

plt.hist(x1, **kwargs, color='red', label='Extinct')
plt.hist(x2, **kwargs, color='orange', label='Critically Endangered')
plt.hist(x3, **kwargs, color='yellow', label='Endangered')
plt.hist(x4, **kwargs, color='green', label='Near Threatened')
plt.hist(x5, **kwargs, color='blue', label='Vulnerable')
plt.hist(x6, **kwargs, color='gray', label='Least Concern')

plt.gca().set(title='Conservation Status', ylabel='Min Wingspan')
plt.legend();

ดูเหมือนว่าจะไม่มีความสัมพันธ์ที่ดีระหว่างความกว้างปีกขั้นต่ำและสถานะการอนุรักษ์ ลองทดสอบองค์ประกอบอื่น ๆ ในชุดข้อมูลโดยใช้วิธีนี้ คุณสามารถลองใช้ตัวกรองที่แตกต่างกันได้ คุณพบความสัมพันธ์ใดหรือไม่?

แผนภูมิความหนาแน่น

คุณอาจสังเกตเห็นว่าฮิสโตแกรมที่เราดูจนถึงตอนนี้มีลักษณะเป็น 'ขั้นบันได' และไม่ได้ไหลอย่างราบรื่นในรูปแบบโค้ง หากต้องการแสดงแผนภูมิความหนาแน่นที่ราบรื่นขึ้น คุณสามารถลองใช้แผนภูมิความหนาแน่น

ในการทำงานกับแผนภูมิความหนาแน่น ให้ทำความคุ้นเคยกับไลบรารีการสร้างแผนภูมิใหม่ Seaborn

โหลด Seaborn และลองสร้างแผนภูมิความหนาแน่นพื้นฐาน:

import seaborn as sns
import matplotlib.pyplot as plt
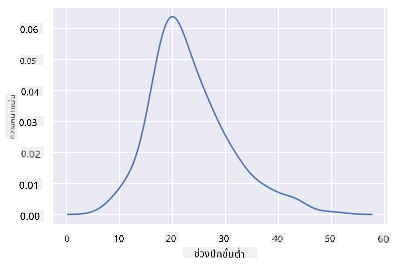
sns.kdeplot(filteredBirds['MinWingspan'])
plt.show()

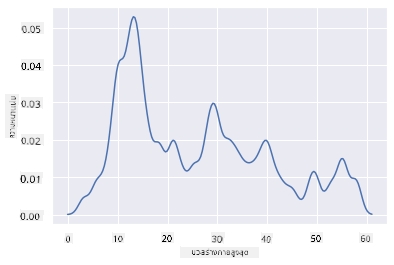
คุณสามารถเห็นได้ว่าแผนภูมิสะท้อนแผนภูมิก่อนหน้านี้สำหรับข้อมูลความกว้างปีกขั้นต่ำ เพียงแต่ราบรื่นขึ้นเล็กน้อย ตามเอกสารของ Seaborn "เมื่อเทียบกับฮิสโตแกรม KDE สามารถสร้างแผนภูมิที่ดูไม่รกและตีความได้ง่ายกว่า โดยเฉพาะเมื่อวาดการกระจายตัวหลายแบบ แต่ก็มีโอกาสที่จะเกิดการบิดเบือนหากการกระจายตัวพื้นฐานมีขอบเขตหรือไม่ราบรื่น" source กล่าวอีกนัยหนึ่ง ค่าผิดปกติจะทำให้แผนภูมิของคุณแสดงผลไม่ดีเสมอ

หากคุณต้องการกลับไปดูเส้น MaxBodyMass ที่เป็นขั้นบันไดในแผนภูมิที่สองที่คุณสร้าง คุณสามารถทำให้มันราบรื่นได้ดีมากโดยสร้างใหม่ด้วยวิธีนี้:

sns.kdeplot(filteredBirds['MaxBodyMass'])
plt.show()

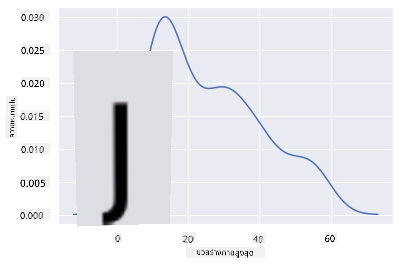
หากคุณต้องการเส้นที่ราบรื่นแต่ไม่ราบรื่นเกินไป ให้แก้ไขพารามิเตอร์ bw_adjust:

sns.kdeplot(filteredBirds['MaxBodyMass'], bw_adjust=.2)
plt.show()

✅ อ่านเกี่ยวกับพารามิเตอร์ที่มีสำหรับแผนภูมิประเภทนี้และทดลองใช้!

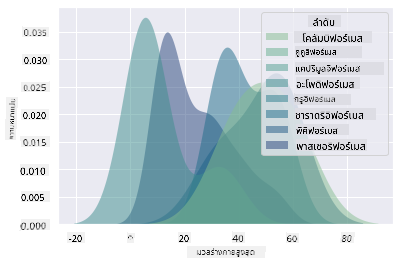
แผนภูมิประเภทนี้ให้การแสดงภาพที่อธิบายได้อย่างสวยงาม ด้วยโค้ดเพียงไม่กี่บรรทัด ตัวอย่างเช่น คุณสามารถแสดงความหนาแน่นของมวลร่างกายสูงสุดต่ออันดับของนก:

sns.kdeplot(
   data=filteredBirds, x="MaxBodyMass", hue="Order",
   fill=True, common_norm=False, palette="crest",
   alpha=.5, linewidth=0,
)

คุณยังสามารถทำแผนที่ความหนาแน่นของตัวแปรหลายตัวในแผนภูมิเดียวกันได้ ลองเปรียบเทียบ MaxLength และ MinLength ของนกกับสถานะการอนุรักษ์:

sns.kdeplot(data=filteredBirds, x="MinLength", y="MaxLength", hue="ConservationStatus")

บางทีอาจคุ้มค่าที่จะวิจัยว่ากลุ่มของนกที่ 'มีแนวโน้มใกล้สูญพันธุ์' ตามความยาวของพวกมันมีความหมายหรือไม่

🚀 ความท้าทาย

ฮิสโตแกรมเป็นแผนภูมิที่ซับซ้อนกว่าการกระจายจุด แผนภูมิแท่ง หรือแผนภูมิเส้นพื้นฐาน ลองค้นหาตัวอย่างการใช้ฮิสโตแกรมที่ดีบนอินเทอร์เน็ต พวกมันถูกใช้ในลักษณะใด แสดงอะไร และมักถูกใช้ในสาขาหรือพื้นที่ใด?

แบบทดสอบหลังเรียน

ทบทวนและศึกษาด้วยตนเอง

ในบทเรียนนี้ คุณได้ใช้ Matplotlib และเริ่มทำงานกับ Seaborn เพื่อแสดงแผนภูมิที่ซับซ้อนมากขึ้น ลองค้นคว้าเกี่ยวกับ kdeplot ใน Seaborn ซึ่งเป็น "เส้นโค้งความน่าจะเป็นต่อเนื่องในหนึ่งหรือหลายมิติ" อ่าน เอกสาร เพื่อทำความเข้าใจวิธีการทำงาน

งานที่ได้รับมอบหมาย

นำทักษะของคุณไปใช้

ข้อจำกัดความรับผิดชอบ:
เอกสารนี้ได้รับการแปลโดยใช้บริการแปลภาษา AI Co-op Translator แม้ว่าเราจะพยายามให้การแปลมีความถูกต้อง แต่โปรดทราบว่าการแปลอัตโนมัติอาจมีข้อผิดพลาดหรือความไม่แม่นยำ เอกสารต้นฉบับในภาษาดั้งเดิมควรถือเป็นแหล่งข้อมูลที่เชื่อถือได้ สำหรับข้อมูลที่สำคัญ แนะนำให้ใช้บริการแปลภาษาจากผู้เชี่ยวชาญ เราไม่รับผิดชอบต่อความเข้าใจผิดหรือการตีความที่ผิดพลาดซึ่งเกิดจากการใช้การแปลนี้