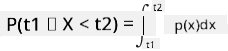History

leestott 96f3257873 🌐 Update translations via Co-op Translator		4 weeks ago
..
README.md	🌐 Update translations via Co-op Translator	4 weeks ago
assignment.md	🌐 Update translations via Co-op Translator	4 weeks ago

README.md

Unescape Escape

Een Korte Introductie tot Statistiek en Kansrekening


Statistiek en Kansrekening - Sketchnote door @nitya

Statistiek en Kansrekening zijn twee sterk verwante gebieden binnen de Wiskunde die zeer relevant zijn voor Data Science. Het is mogelijk om met data te werken zonder diepgaande kennis van wiskunde, maar het is toch beter om ten minste enkele basisconcepten te begrijpen. Hier bieden we een korte introductie die je op weg helpt.

Quiz voorafgaand aan de les

Kansrekening en Willekeurige Variabelen

Kans is een getal tussen 0 en 1 dat uitdrukt hoe waarschijnlijk een gebeurtenis is. Het wordt gedefinieerd als het aantal positieve uitkomsten (die leiden tot de gebeurtenis), gedeeld door het totale aantal uitkomsten, ervan uitgaande dat alle uitkomsten even waarschijnlijk zijn. Bijvoorbeeld, als we een dobbelsteen gooien, is de kans op een even getal 3/6 = 0,5.

Wanneer we over gebeurtenissen praten, gebruiken we willekeurige variabelen. Bijvoorbeeld, de willekeurige variabele die het getal vertegenwoordigt dat wordt gegooid met een dobbelsteen, kan waarden aannemen van 1 tot 6. De verzameling getallen van 1 tot 6 wordt de steekproefruimte genoemd. We kunnen praten over de kans dat een willekeurige variabele een bepaalde waarde aanneemt, bijvoorbeeld P(X=3)=1/6.

De willekeurige variabele in het vorige voorbeeld wordt discreet genoemd, omdat het een telbare steekproefruimte heeft, d.w.z. er zijn afzonderlijke waarden die kunnen worden opgesomd. Er zijn gevallen waarin de steekproefruimte een bereik van reële getallen is, of de gehele verzameling reële getallen. Dergelijke variabelen worden continu genoemd. Een goed voorbeeld is de aankomsttijd van een bus.

Kansverdeling

In het geval van discrete willekeurige variabelen is het eenvoudig om de kans van elke gebeurtenis te beschrijven met een functie P(X). Voor elke waarde s uit de steekproefruimte S geeft deze een getal tussen 0 en 1, zodanig dat de som van alle waarden van P(X=s) voor alle gebeurtenissen gelijk is aan 1.

De meest bekende discrete verdeling is de uniforme verdeling, waarbij er een steekproefruimte is van N elementen, met een gelijke kans van 1/N voor elk van hen.

Het is moeilijker om de kansverdeling van een continue variabele te beschrijven, met waarden uit een interval [a,b], of de gehele verzameling reële getallen ℝ. Neem bijvoorbeeld de aankomsttijd van een bus. In feite is de kans dat een bus precies op een bepaald tijdstip t aankomt, 0!

Nu weet je dat gebeurtenissen met kans 0 toch gebeuren, en vaak zelfs! Bijvoorbeeld elke keer dat de bus aankomt!

We kunnen alleen spreken over de kans dat een variabele binnen een bepaald interval van waarden valt, bijvoorbeeld P(t₁≤X<t₂). In dit geval wordt de kansverdeling beschreven door een kansdichtheidsfunctie p(x), zodanig dat

$P(t_1\le X<t_2)=\int_{t_1}^{t_2}p(x)dx$

Een continue variant van de uniforme verdeling wordt continue uniforme verdeling genoemd, die wordt gedefinieerd op een eindig interval. De kans dat de waarde X in een interval van lengte l valt, is evenredig aan l en loopt op tot 1.

Een andere belangrijke verdeling is de normale verdeling, waar we hieronder meer in detail op ingaan.

Gemiddelde, Variantie en Standaarddeviatie

Stel dat we een reeks van n steekproeven van een willekeurige variabele X trekken: x₁, x₂, ..., x_n. We kunnen de gemiddelde (of rekenkundige gemiddelde) waarde van de reeks op de traditionele manier definiëren als (x₁+x₂+x_n)/n. Naarmate we de steekproefgrootte vergroten (d.w.z. de limiet nemen met n→∞), verkrijgen we het gemiddelde (ook wel verwachtingswaarde genoemd) van de verdeling. We noteren de verwachtingswaarde met E(x).

Het kan worden aangetoond dat voor elke discrete verdeling met waarden {x₁, x₂, ..., x_N} en bijbehorende kansen p₁, p₂, ..., p_N, de verwachtingswaarde gelijk is aan E(X)=x₁p₁+x₂p₂+...+x_Np_N.

Om te bepalen hoe ver de waarden verspreid zijn, kunnen we de variantie berekenen: σ² = ∑(x_i - μ)²/n, waarbij μ het gemiddelde van de reeks is. De waarde σ wordt de standaarddeviatie genoemd, en σ² wordt de variantie genoemd.

Modus, Mediaan en Kwartielen

Soms geeft het gemiddelde geen goed beeld van de "typische" waarde van data. Bijvoorbeeld, wanneer er enkele extreme waarden zijn die volledig buiten het bereik liggen, kunnen deze het gemiddelde beïnvloeden. Een andere goede indicator is de mediaan, een waarde zodanig dat de helft van de datapunten lager is en de andere helft hoger.

Om de verdeling van data beter te begrijpen, is het nuttig om te praten over kwartielen:

Het eerste kwartiel, of Q1, is een waarde waarbij 25% van de data eronder valt.
Het derde kwartiel, of Q3, is een waarde waarbij 75% van de data eronder valt.

Grafisch kunnen we de relatie tussen mediaan en kwartielen weergeven in een diagram dat een boxplot wordt genoemd:

Hier berekenen we ook de interkwartielafstand IQR=Q3-Q1, en zogenaamde uitbijters - waarden die buiten de grenzen [Q1-1.5IQR,Q3+1.5IQR] liggen.

Voor een eindige verdeling met een klein aantal mogelijke waarden is een goede "typische" waarde degene die het vaakst voorkomt, de modus. Dit wordt vaak toegepast op categorische data, zoals kleuren. Stel je een situatie voor waarin we twee groepen mensen hebben - sommigen die sterk de voorkeur geven aan rood, en anderen die blauw prefereren. Als we kleuren coderen met nummers, zou de gemiddelde waarde voor een favoriete kleur ergens in het oranje-groene spectrum liggen, wat geen echte voorkeur van een van beide groepen aangeeft. De modus zou echter een van de kleuren zijn, of beide kleuren, als het aantal mensen dat ervoor stemt gelijk is (in dat geval noemen we de steekproef multimodaal).

Data uit de Werkelijkheid

Wanneer we data uit het echte leven analyseren, zijn deze vaak geen willekeurige variabelen in de strikte zin, omdat we geen experimenten uitvoeren met onbekende uitkomsten. Neem bijvoorbeeld een team van honkbalspelers en hun lichaamsgegevens, zoals lengte, gewicht en leeftijd. Deze cijfers zijn niet echt willekeurig, maar we kunnen nog steeds dezelfde wiskundige concepten toepassen. Bijvoorbeeld, een reeks gewichten van mensen kan worden beschouwd als een reeks waarden getrokken uit een willekeurige variabele. Hieronder staat de reeks gewichten van echte honkbalspelers uit de Major League Baseball, afkomstig uit deze dataset (voor jouw gemak zijn alleen de eerste 20 waarden weergegeven):

[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]

Opmerking: Om een voorbeeld te zien van het werken met deze dataset, bekijk de bijbehorende notebook. Er zijn ook een aantal uitdagingen in deze les, en je kunt deze voltooien door wat code toe te voegen aan die notebook. Als je niet zeker weet hoe je met data moet werken, maak je geen zorgen - we komen later terug op het werken met data in Python. Als je niet weet hoe je code uitvoert in Jupyter Notebook, bekijk dan dit artikel.

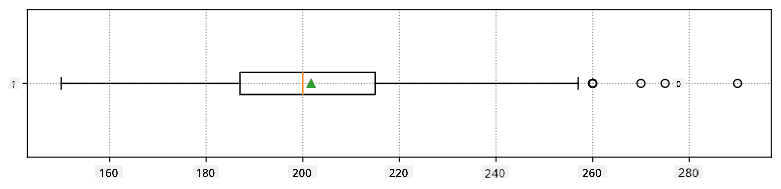
Hier is de boxplot die het gemiddelde, de mediaan en de kwartielen voor onze data toont:

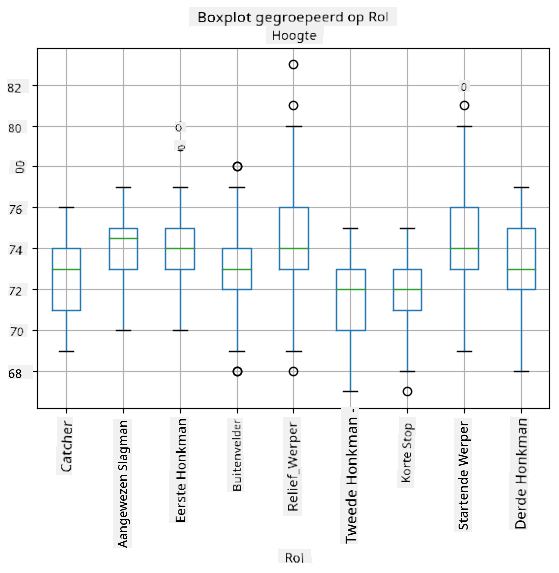
Omdat onze data informatie bevat over verschillende speler rollen, kunnen we ook een boxplot per rol maken - dit geeft ons een idee van hoe de parameters verschillen per rol. Deze keer bekijken we de lengte:

Dit diagram suggereert dat de lengte van eerste honkspelers gemiddeld hoger is dan die van tweede honkspelers. Later in deze les leren we hoe we deze hypothese formeler kunnen testen en hoe we kunnen aantonen dat onze data statistisch significant is om dit te bewijzen.

Bij het werken met data uit de werkelijkheid gaan we ervan uit dat alle datapunten steekproeven zijn getrokken uit een bepaalde kansverdeling. Deze aanname stelt ons in staat om machine learning-technieken toe te passen en werkende voorspellende modellen te bouwen.

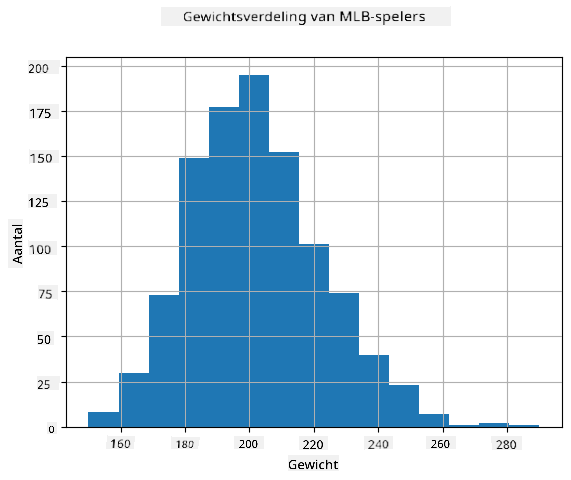
Om te zien wat de verdeling van onze data is, kunnen we een grafiek maken die een histogram wordt genoemd. De X-as bevat een aantal verschillende gewichtintervallen (de zogenaamde bins), en de verticale as toont het aantal keren dat onze steekproef van de willekeurige variabele binnen een bepaald interval viel.

Uit dit histogram kun je zien dat alle waarden gecentreerd zijn rond een bepaald gemiddeld gewicht, en hoe verder we van dat gewicht af gaan, hoe minder vaak gewichten van die waarde voorkomen. Met andere woorden, het is zeer onwaarschijnlijk dat het gewicht van een honkbalspeler sterk afwijkt van het gemiddelde gewicht. De variantie van gewichten laat zien in hoeverre gewichten waarschijnlijk verschillen van het gemiddelde.

Als we gewichten van andere mensen nemen, niet uit de honkbalcompetitie, is de verdeling waarschijnlijk anders. De vorm van de verdeling blijft echter hetzelfde, maar het gemiddelde en de variantie zouden veranderen. Dus, als we ons model trainen op honkbalspelers, is het waarschijnlijk dat het verkeerde resultaten geeft wanneer het wordt toegepast op studenten van een universiteit, omdat de onderliggende verdeling anders is.

Normale Verdeling

De verdeling van gewichten die we hierboven hebben gezien, is zeer typisch, en veel metingen uit de werkelijkheid volgen hetzelfde type verdeling, maar met een ander gemiddelde en een andere variantie. Deze verdeling wordt de normale verdeling genoemd en speelt een zeer belangrijke rol in de statistiek.

Het gebruik van een normale verdeling is een correcte manier om willekeurige gewichten van potentiële honkbalspelers te genereren. Zodra we het gemiddelde gewicht mean en de standaarddeviatie std kennen, kunnen we 1000 gewichtsmonsters genereren op de volgende manier:

samples = np.random.normal(mean,std,1000)

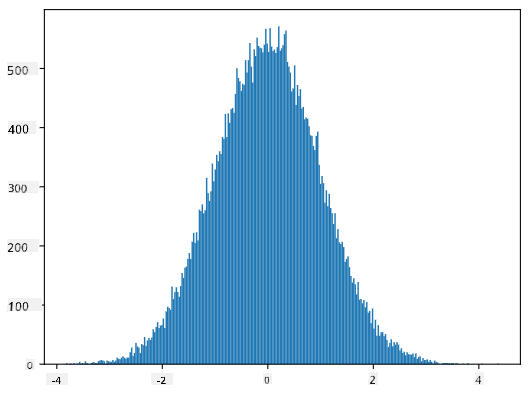
Als we het histogram van de gegenereerde monsters plotten, zien we een afbeelding die erg lijkt op de bovenstaande. En als we het aantal monsters en het aantal bins vergroten, kunnen we een afbeelding van een normale verdeling genereren die dichter bij ideaal is:

Normale Verdeling met mean=0 en std.dev=1

Betrouwbaarheidsintervallen

Wanneer we het hebben over gewichten van honkbalspelers, gaan we ervan uit dat er een bepaalde willekeurige variabele W is die overeenkomt met de ideale kansverdeling van gewichten van alle honkbalspelers (de zogenaamde populatie). Onze reeks gewichten komt overeen met een subset van alle honkbalspelers die we een steekproef noemen. Een interessante vraag is: kunnen we de parameters van de verdeling van W kennen, d.w.z. het gemiddelde en de variantie van de populatie?

Het eenvoudigste antwoord zou zijn om het gemiddelde en de variantie van onze steekproef te berekenen. Het kan echter gebeuren dat onze willekeurige steekproef de volledige populatie niet nauwkeurig vertegenwoordigt. Daarom is het logisch om te spreken over betrouwbaarheidsintervallen.

Betrouwbaarheidsinterval is de schatting van het werkelijke gemiddelde van de populatie op basis van onze steekproef, die met een bepaalde waarschijnlijkheid (of betrouwbaarheidsniveau) nauwkeurig is. Stel dat we een steekproef X₁, ..., X_n hebben uit onze verdeling. Elke keer dat we een steekproef trekken uit onze verdeling, krijgen we een andere gemiddelde waarde μ. Daarom kan μ worden beschouwd als een willekeurige variabele. Een betrouwbaarheidsinterval met betrouwbaarheid p is een paar waarden (L_p,R_p), zodanig dat P(L_p≤μ≤R_p) = p, oftewel de kans dat de gemeten gemiddelde waarde binnen het interval valt, is gelijk aan p.

Het gaat verder dan onze korte introductie om in detail te bespreken hoe deze betrouwbaarheidsintervallen worden berekend. Meer details zijn te vinden op Wikipedia. Kort gezegd definiëren we de verdeling van het berekende steekproefgemiddelde ten opzichte van het werkelijke gemiddelde van de populatie, wat de studentverdeling wordt genoemd.

Interessant feit: De studentverdeling is vernoemd naar wiskundige William Sealy Gosset, die zijn artikel publiceerde onder het pseudoniem "Student". Hij werkte in de Guinness-brouwerij, en volgens een van de verhalen wilde zijn werkgever niet dat het grote publiek wist dat ze statistische tests gebruikten om de kwaliteit van grondstoffen te bepalen.

Als we het gemiddelde μ van onze populatie willen schatten met betrouwbaarheid p, moeten we het (1-p)/2-de percentiel van een studentverdeling A nemen, die ofwel uit tabellen kan worden gehaald, of kan worden berekend met ingebouwde functies van statistische software (bijv. Python, R, enz.). Dan wordt het interval voor μ gegeven door X±A*D/√n, waarbij X het verkregen gemiddelde van de steekproef is en D de standaardafwijking.

Opmerking: We laten ook de bespreking van een belangrijk concept, namelijk vrijheidsgraden, achterwege, wat belangrijk is in relatie tot de studentverdeling. Je kunt meer uitgebreide boeken over statistiek raadplegen om dit concept dieper te begrijpen.

Een voorbeeld van het berekenen van een betrouwbaarheidsinterval voor gewichten en lengtes is te vinden in de bijbehorende notebooks.

p	Gemiddelde gewicht
0.85	201.73±0.94
0.90	201.73±1.08
0.95	201.73±1.28

Merk op dat hoe hoger de betrouwbaarheidskans is, hoe breder het betrouwbaarheidsinterval wordt.

Hypothesetoetsing

In onze dataset van honkbalspelers zijn er verschillende spelersrollen, die als volgt kunnen worden samengevat (bekijk de bijbehorende notebook om te zien hoe deze tabel kan worden berekend):

Rol	Lengte	Gewicht	Aantal
Catcher	72.723684	204.328947	76
Designated_Hitter	74.222222	220.888889	18
First_Baseman	74.000000	213.109091	55
Outfielder	73.010309	199.113402	194
Relief_Pitcher	74.374603	203.517460	315
Second_Baseman	71.362069	184.344828	58
Shortstop	71.903846	182.923077	52
Starting_Pitcher	74.719457	205.163636	221
Third_Baseman	73.044444	200.955556	45

We kunnen zien dat de gemiddelde lengte van eerste honkspelers hoger is dan die van tweede honkspelers. Daarom kunnen we geneigd zijn te concluderen dat eerste honkspelers langer zijn dan tweede honkspelers.

Deze uitspraak wordt een hypothese genoemd, omdat we niet weten of het feit daadwerkelijk waar is.

Het is echter niet altijd duidelijk of we deze conclusie kunnen trekken. Uit de bovenstaande discussie weten we dat elk gemiddelde een bijbehorend betrouwbaarheidsinterval heeft, en dat dit verschil dus gewoon een statistische fout kan zijn. We hebben een meer formele manier nodig om onze hypothese te testen.

Laten we betrouwbaarheidsintervallen afzonderlijk berekenen voor de lengtes van eerste en tweede honkspelers:

Betrouwbaarheid	Eerste honkspelers	Tweede honkspelers
0.85	73.62..74.38	71.04..71.69
0.90	73.56..74.44	70.99..71.73
0.95	73.47..74.53	70.92..71.81

We kunnen zien dat de intervallen onder geen enkele betrouwbaarheid overlappen. Dat bewijst onze hypothese dat eerste honkspelers langer zijn dan tweede honkspelers.

Formeler gezegd is het probleem dat we proberen op te lossen om te zien of twee kansverdelingen hetzelfde zijn, of op zijn minst dezelfde parameters hebben. Afhankelijk van de verdeling moeten we daarvoor verschillende tests gebruiken. Als we weten dat onze verdelingen normaal zijn, kunnen we de Student t-test toepassen.

Bij de Student t-test berekenen we de zogenaamde t-waarde, die het verschil tussen gemiddelden aangeeft, rekening houdend met de variantie. Het is aangetoond dat de t-waarde de studentverdeling volgt, wat ons in staat stelt de drempelwaarde te verkrijgen voor een gegeven betrouwbaarheidsniveau p (dit kan worden berekend of opgezocht in numerieke tabellen). We vergelijken vervolgens de t-waarde met deze drempel om de hypothese goed te keuren of te verwerpen.

In Python kunnen we het SciPy-pakket gebruiken, dat de functie ttest_ind bevat (naast vele andere nuttige statistische functies!). Deze functie berekent de t-waarde voor ons en doet ook de omgekeerde lookup van de betrouwbaarheids-p-waarde, zodat we alleen naar de betrouwbaarheid hoeven te kijken om een conclusie te trekken.

Bijvoorbeeld, onze vergelijking tussen de lengtes van eerste en tweede honkspelers geeft ons de volgende resultaten:

from scipy.stats import ttest_ind

tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")

T-value = 7.65
P-value: 9.137321189738925e-12

In ons geval is de p-waarde zeer laag, wat betekent dat er sterk bewijs is dat eerste honkspelers langer zijn.

Er zijn ook andere soorten hypothesen die we mogelijk willen testen, bijvoorbeeld:

Bewijzen dat een bepaalde steekproef een bepaalde verdeling volgt. In ons geval hebben we aangenomen dat lengtes normaal verdeeld zijn, maar dat vereist formele statistische verificatie.
Bewijzen dat een gemiddelde waarde van een steekproef overeenkomt met een vooraf gedefinieerde waarde.
Vergelijken van gemiddelden van meerdere steekproeven (bijv. wat is het verschil in geluksniveaus tussen verschillende leeftijdsgroepen).

Wet van de grote aantallen en centrale limietstelling

Een van de redenen waarom de normale verdeling zo belangrijk is, is de zogenaamde centrale limietstelling. Stel dat we een grote steekproef hebben van onafhankelijke N waarden X₁, ..., X_N, getrokken uit een willekeurige verdeling met gemiddelde μ en variantie σ². Dan, voor voldoende grote N (met andere woorden, wanneer N→∞), zal het gemiddelde Σ_iX_i normaal verdeeld zijn, met gemiddelde μ en variantie σ²/N.

Een andere manier om de centrale limietstelling te interpreteren is te zeggen dat, ongeacht de verdeling, wanneer je het gemiddelde berekent van een som van willekeurige variabelen, je uitkomt op een normale verdeling.

Uit de centrale limietstelling volgt ook dat, wanneer N→∞, de kans dat het steekproefgemiddelde gelijk is aan μ, 1 wordt. Dit staat bekend als de wet van de grote aantallen.

Covariantie en correlatie

Een van de dingen die Data Science doet, is het vinden van relaties tussen gegevens. We zeggen dat twee reeksen correleren wanneer ze hetzelfde gedrag vertonen op hetzelfde moment, d.w.z. ze stijgen/dalen tegelijkertijd, of de ene reeks stijgt wanneer de andere daalt en vice versa. Met andere woorden, er lijkt een relatie te zijn tussen twee reeksen.

Correlatie geeft niet noodzakelijk een oorzakelijk verband aan tussen twee reeksen; soms kunnen beide variabelen afhankelijk zijn van een externe oorzaak, of het kan puur toeval zijn dat de twee reeksen correleren. Sterke wiskundige correlatie is echter een goede indicatie dat twee variabelen op de een of andere manier verbonden zijn.

Wiskundig gezien is het belangrijkste concept dat de relatie tussen twee willekeurige variabelen laat zien covariantie, die als volgt wordt berekend: Cov(X,Y) = E[(X-E(X))(Y-E(Y))]. We berekenen de afwijking van beide variabelen ten opzichte van hun gemiddelde waarden, en vervolgens het product van die afwijkingen. Als beide variabelen samen afwijken, zal het product altijd een positieve waarde zijn, wat optelt tot een positieve covariantie. Als beide variabelen niet synchroon afwijken (d.w.z. de ene daalt onder het gemiddelde wanneer de andere boven het gemiddelde stijgt), krijgen we altijd negatieve getallen, die optellen tot een negatieve covariantie. Als de afwijkingen niet afhankelijk zijn, zullen ze optellen tot ongeveer nul.

De absolute waarde van covariantie zegt niet veel over hoe groot de correlatie is, omdat het afhangt van de grootte van de werkelijke waarden. Om het te normaliseren, kunnen we de covariantie delen door de standaardafwijking van beide variabelen, om correlatie te krijgen. Het goede is dat correlatie altijd in het bereik van [-1,1] ligt, waarbij 1 een sterke positieve correlatie tussen waarden aangeeft, -1 een sterke negatieve correlatie, en 0 helemaal geen correlatie (variabelen zijn onafhankelijk).

Voorbeeld: We kunnen de correlatie berekenen tussen gewichten en lengtes van honkbalspelers uit de eerder genoemde dataset:

print(np.corrcoef(weights,heights))

Als resultaat krijgen we een correlatiematrix zoals deze:

array([[1.        , 0.52959196],
       [0.52959196, 1.        ]])

Een correlatiematrix C kan worden berekend voor elk aantal invoerreeksen S₁, ..., S_n. De waarde van C_ij is de correlatie tussen S_i en S_j, en diagonale elementen zijn altijd 1 (wat ook zelfcorrelatie van S_i is).

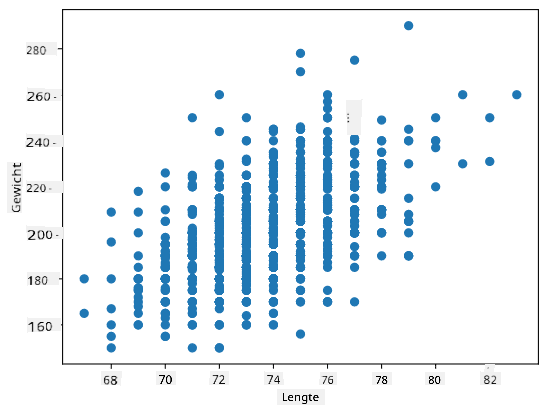
In ons geval geeft de waarde 0.53 aan dat er enige correlatie is tussen het gewicht en de lengte van een persoon. We kunnen ook een spreidingsdiagram maken van de ene waarde tegen de andere om de relatie visueel te zien:

Meer voorbeelden van correlatie en covariantie zijn te vinden in de bijbehorende notebook.

Conclusie

In deze sectie hebben we geleerd:

basisstatistische eigenschappen van gegevens, zoals gemiddelde, variantie, modus en kwartielen
verschillende verdelingen van willekeurige variabelen, inclusief normale verdeling
hoe correlatie tussen verschillende eigenschappen te vinden
hoe het wiskundige en statistische apparaat te gebruiken om hypothesen te bewijzen
hoe betrouwbaarheidsintervallen te berekenen voor een willekeurige variabele op basis van een steekproef

Hoewel dit zeker geen uitputtende lijst is van onderwerpen binnen waarschijnlijkheid en statistiek, zou het voldoende moeten zijn om je een goede start te geven in deze cursus.

🚀 Uitdaging

Gebruik de voorbeeldcode in de notebook om andere hypothesen te testen:

Eerste honkspelers zijn ouder dan tweede honkspelers
Eerste honkspelers zijn langer dan derde honkspelers
Shortstops zijn langer dan tweede honkspelers

Post-lecture quiz

Review & Zelfstudie

Waarschijnlijkheid en statistiek is zo'n breed onderwerp dat het een eigen cursus verdient. Als je dieper in de theorie wilt duiken, kun je enkele van de volgende boeken lezen:

Carlos Fernandez-Granda van New York University heeft geweldige collegedictaten Probability and Statistics for Data Science (online beschikbaar)
Peter en Andrew Bruce. Practical Statistics for Data Scientists. [voorbeeldcode in R].
James D. Miller. Statistics for Data Science [voorbeeldcode in R]

Opdracht

Kleine Diabetesstudie

Credits

Deze les is met ♥️ geschreven door Dmitry Soshnikov

Disclaimer:
Dit document is vertaald met behulp van de AI-vertalingsservice Co-op Translator. Hoewel we streven naar nauwkeurigheid, dient u zich ervan bewust te zijn dat geautomatiseerde vertalingen fouten of onnauwkeurigheden kunnen bevatten. Het originele document in de oorspronkelijke taal moet worden beschouwd als de gezaghebbende bron. Voor cruciale informatie wordt professionele menselijke vertaling aanbevolen. Wij zijn niet aansprakelijk voor eventuele misverstanden of verkeerde interpretaties die voortvloeien uit het gebruik van deze vertaling.

README.md Unescape Escape