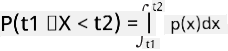History

leestott 5391b4bc5f 🌐 Update translations via Co-op Translator		3 weeks ago
..
README.md	🌐 Update translations via Co-op Translator	3 weeks ago
assignment.md	🌐 Update translations via Co-op Translator	3 weeks ago

README.md

Unescape Escape

तथ्यांक र सम्भाव्यता: संक्षिप्त परिचय


तथ्यांक र सम्भाव्यता - Sketchnote by @nitya

तथ्यांक र सम्भाव्यता सिद्धान्त गणितका दुई अत्यन्त सम्बन्धित क्षेत्रहरू हुन्, जुन डेटा विज्ञानका लागि अत्यन्त महत्त्वपूर्ण छन्। गहिरो गणितीय ज्ञान बिना पनि डेटा प्रयोग गर्न सकिन्छ, तर कम्तीमा केही आधारभूत अवधारणाहरू थाहा हुनु राम्रो हुन्छ। यहाँ हामी तपाईंलाई सुरु गर्न मद्दत गर्ने छोटो परिचय प्रस्तुत गर्नेछौं।

Pre-lecture quiz

सम्भाव्यता र र्‍यान्डम भेरिएबलहरू

सम्भाव्यता ० र १ को बीचको संख्या हो, जसले कुनै घटना कति सम्भाव्य छ भन्ने व्यक्त गर्दछ। यो सकारात्मक परिणामहरूको संख्या (जसले घटनालाई निम्त्याउँछ) लाई कुल परिणामहरूको संख्याले भाग गरेर परिभाषित गरिन्छ, यदि सबै परिणामहरू समान सम्भाव्य छन् भने। उदाहरणका लागि, जब हामी पासा फाल्छौं, सम संख्या आउने सम्भाव्यता 3/6 = 0.5 हुन्छ।

जब हामी घटनाहरूको कुरा गर्छौं, हामी र्‍यान्डम भेरिएबलहरू प्रयोग गर्छौं। उदाहरणका लागि, पासा फाल्दा प्राप्त हुने संख्यालाई प्रतिनिधित्व गर्ने र्‍यान्डम भेरिएबलले १ देखि ६ सम्मका मानहरू लिन्छ। १ देखि ६ सम्मको संख्याको सेटलाई नमूना स्थान भनिन्छ। हामी र्‍यान्डम भेरिएबलले कुनै निश्चित मान लिने सम्भाव्यताको कुरा गर्न सक्छौं, जस्तै P(X=3)=1/6।

अघिल्लो उदाहरणमा रहेको र्‍यान्डम भेरिएबललाई डिस्क्रिट भनिन्छ, किनभने यससँग गणनायोग्य नमूना स्थान छ, अर्थात् छुट्टाछुट्टै मानहरू छन् जसलाई गन्न सकिन्छ। केही अवस्थामा नमूना स्थान वास्तविक संख्याहरूको दायरा वा सम्पूर्ण वास्तविक संख्याहरूको सेट हुन सक्छ। यस्ता भेरिएबलहरूलाई कन्टिन्युअस भनिन्छ। यसको राम्रो उदाहरण बस आउने समय हो।

सम्भाव्यता वितरण

डिस्क्रिट र्‍यान्डम भेरिएबलहरूको सन्दर्भमा, प्रत्येक घटनाको सम्भाव्यता P(X) नामक कार्यद्वारा वर्णन गर्न सजिलो हुन्छ। नमूना स्थान S बाट प्रत्येक मान s का लागि, यसले ० देखि १ सम्मको संख्या दिन्छ, जसमा सबै घटनाहरूको लागि P(X=s) को कुल योग १ हुन्छ।

सबैभन्दा प्रख्यात डिस्क्रिट वितरण यूनिफर्म वितरण हो, जसमा N तत्वहरूको नमूना स्थान हुन्छ, र प्रत्येकको सम्भाव्यता 1/N हुन्छ।

कन्टिन्युअस भेरिएबलको सम्भाव्यता वितरण वर्णन गर्न अलि गाह्रो हुन्छ, जसका मानहरू [a,b] अन्तराल वा सम्पूर्ण वास्तविक संख्याहरू ℝ बाट लिइन्छ। बस आउने समयको उदाहरणलाई विचार गर्नुहोस्। वास्तवमा, कुनै निश्चित समय t मा बस ठीक त्यही समयमा आउने सम्भाव्यता ० हुन्छ!

अब तपाईंलाई थाहा भयो कि ० सम्भाव्यता भएका घटनाहरू पनि हुन्छन्, र धेरैपटक हुन्छन्! कम्तीमा बस आउने प्रत्येक पटक!

हामी केवल कुनै भेरिएबलले कुनै निश्चित मानहरूको अन्तरालमा पर्ने सम्भाव्यताको कुरा गर्न सक्छौं, जस्तै P(t₁≤X<t₂)। यस अवस्थामा, सम्भाव्यता वितरणलाई सम्भाव्यता घनत्व कार्य p(x) द्वारा वर्णन गरिन्छ, जसले

$P(t_1\le X<t_2)=\int_{t_1}^{t_2}p(x)dx$

कन्टिन्युअस यूनिफर्म वितरणको निरन्तर संस्करण कन्टिन्युअस यूनिफर्म हो, जुन सीमित अन्तरालमा परिभाषित हुन्छ। मान X ले लम्बाइ l को अन्तरालमा पर्ने सम्भाव्यता l को अनुपातमा हुन्छ, र १ सम्म बढ्छ।

अर्को महत्त्वपूर्ण वितरण नर्मल वितरण हो, जसको बारेमा हामी तल थप विवरणमा कुरा गर्नेछौं।

औसत, भिन्नता र मानक विचलन

मानौं हामीले र्‍यान्डम भेरिएबल X का n नमूनाहरूको क्रम निकाल्यौं: x₁, x₂, ..., x_n। हामी परम्परागत तरिकाले औसत (वा अंकगणितीय औसत) मानलाई (x₁+x₂+x_n)/n को रूपमा परिभाषित गर्न सक्छौं। जब हामी नमूनाको आकार बढाउँछौं (अर्थात् n→∞ को सीमा लिन्छौं), हामी वितरणको औसत (जसलाई अपेक्षा पनि भनिन्छ) प्राप्त गर्नेछौं। हामी अपेक्षालाई E(x) द्वारा जनाउनेछौं।

यो देखाउन सकिन्छ कि कुनै पनि डिस्क्रिट वितरणका लागि, जसमा मानहरू {x₁, x₂, ..., x_N} र तिनीहरूको सम्भाव्यता p₁, p₂, ..., p_N छन्, अपेक्षा E(X)=x₁p₁+x₂p₂+...+x_Np_N बराबर हुनेछ।

मानहरू कति फैलिएका छन् भनेर पत्ता लगाउन, हामी भिन्नता σ² = ∑(x_i - μ)²/n गणना गर्न सक्छौं, जहाँ μ अनुक्रमको औसत हो। मान σ लाई मानक विचलन भनिन्छ, र σ² लाई भिन्नता भनिन्छ।

मोड, माध्यिका र क्वार्टाइलहरू

कहिलेकाहीँ, औसतले डेटा प्रतिनिधित्व गर्न पर्याप्त हुँदैन। उदाहरणका लागि, जब केही अत्यधिक मानहरू हुन्छन्, जसले औसतलाई प्रभाव पार्न सक्छ। अर्को राम्रो संकेतक माध्यिका हो, जुन यस्तो मान हो कि आधा डेटा बिन्दुहरू यसभन्दा कम हुन्छन्, र अर्को आधा - बढी।

डेटाको वितरण बुझ्न मद्दत गर्न, क्वार्टाइलहरू को कुरा गर्नु उपयोगी हुन्छ:

पहिलो क्वार्टाइल, वा Q1, यस्तो मान हो, जसमा २५% डेटा यसभन्दा तल पर्छ
तेस्रो क्वार्टाइल, वा Q3, यस्तो मान हो, जसमा ७५% डेटा यसभन्दा तल पर्छ

ग्राफिकल रूपमा, हामी माध्यिका र क्वार्टाइलहरूको सम्बन्धलाई बक्स प्लट मा प्रतिनिधित्व गर्न सक्छौं:

यहाँ हामी इन्टर-क्वार्टाइल रेन्ज IQR=Q3-Q1, र तथाकथित आउटलायर्स - मानहरू, जुन [Q1-1.5IQR,Q3+1.5IQR] सीमाहरू बाहिर पर्छन्, पनि गणना गर्छौं।

यदि वितरणमा सम्भावित मानहरूको संख्या सानो छ भने, राम्रो "सामान्य" मान त्यो हो, जुन सबैभन्दा धेरै पटक देखा पर्छ, जसलाई मोड भनिन्छ। यो प्रायः श्रेणीगत डेटा, जस्तै रङहरूमा लागू हुन्छ। मानौं, हामीसँग दुई समूहका मानिसहरू छन् - केहीले रातो मन पराउँछन्, र केहीले निलो। यदि हामीले रङहरूलाई संख्याहरूद्वारा कोड गर्यौं भने, मनपर्ने रङको औसत मान कतै सुन्तला-हरियो स्पेक्ट्रममा पर्न सक्छ, जसले कुनै पनि समूहको वास्तविक रुचिलाई जनाउँदैन। तर, मोड भने या त एउटा रङ हुनेछ, या दुवै रङ, यदि तिनीहरूको लागि मत दिने मानिसहरूको संख्या समान छ भने (यस अवस्थामा हामी नमूनालाई मल्टिमोडल भन्छौं)।

वास्तविक जीवनको डेटा

जब हामी वास्तविक जीवनको डेटा विश्लेषण गर्छौं, तिनीहरू प्रायः र्‍यान्डम भेरिएबलहरू जस्ता हुँदैनन्, किनभने हामी अज्ञात परिणामसहितको प्रयोग गर्दैनौं। उदाहरणका लागि, बेसबल खेलाडीहरूको टोलीलाई विचार गर्नुहोस्, र तिनीहरूको उचाइ, तौल र उमेर जस्ता शारीरिक डेटा। ती संख्याहरू पूर्ण रूपमा र्‍यान्डम हुँदैनन्, तर हामी अझै पनि उही गणितीय अवधारणाहरू लागू गर्न सक्छौं। उदाहरणका लागि, मानिसहरूको तौलको अनुक्रमलाई केही र्‍यान्डम भेरिएबलबाट लिइएको मानहरूको अनुक्रम मान्न सकिन्छ। तल मेजर लिग बेसबल का वास्तविक खेलाडीहरूको तौलको अनुक्रम छ, जुन यस डेटासेट बाट लिइएको हो (तपाईंको सुविधाका लागि, केवल पहिलो २० मानहरू देखाइएको छ):

[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]

Note: यस डेटासेटसँग काम गर्ने उदाहरण हेर्न, संगत नोटबुक हेर्नुहोस्। यस पाठमा धेरै चुनौतीहरू पनि छन्, र तपाईं ती चुनौतीहरू नोटबुकमा केही कोड थपेर पूरा गर्न सक्नुहुन्छ। यदि तपाईंलाई डेटा सञ्चालन गर्न थाहा छैन भने, चिन्ता नगर्नुहोस् - हामी पछि Python प्रयोग गरेर डेटा सञ्चालनमा फर्कनेछौं। यदि तपाईंलाई Jupyter Notebook मा कोड कसरी चलाउने थाहा छैन भने, यो लेख हेर्नुहोस्।

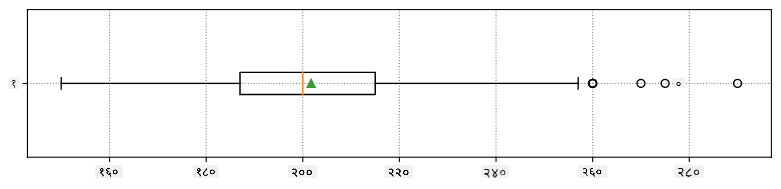
यहाँ हाम्रो डेटाको लागि औसत, माध्यिका र क्वार्टाइलहरू देखाउने बक्स प्लट छ:

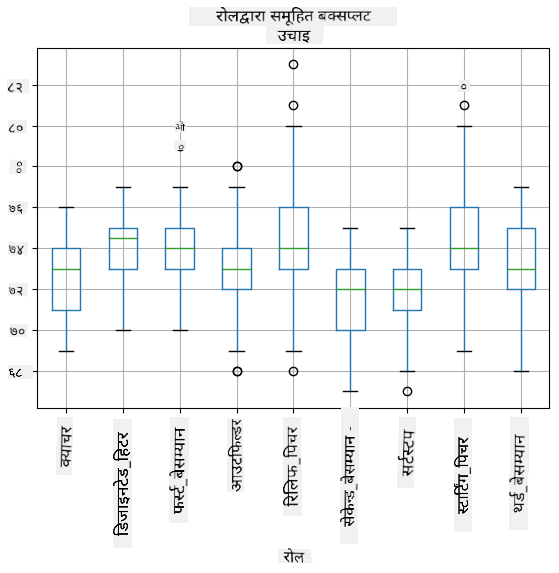
हाम्रो डेटामा विभिन्न खेलाडी भूमिकाहरू को जानकारी समावेश भएकाले, हामी भूमिकाद्वारा बक्स प्लट पनि बनाउन सक्छौं - यसले हामीलाई विभिन्न भूमिकाहरूमा मापदण्ड मानहरू कसरी फरक छन् भन्ने बुझ्न मद्दत गर्दछ। यस पटक हामी उचाइलाई विचार गर्नेछौं:

यो चित्रले सुझाव दिन्छ कि, औसतमा, पहिलो बेसम्यानहरूको उचाइ दोस्रो बेसम्यानहरूको उचाइभन्दा बढी छ। यस पाठको पछि हामी यो परिकल्पनालाई औपचारिक रूपमा कसरी परीक्षण गर्ने, र हाम्रो डेटा सांख्यिकीय रूपमा महत्त्वपूर्ण छ भनेर कसरी प्रदर्शन गर्ने भन्ने कुरा सिक्नेछौं।

जब हामी वास्तविक जीवनको डेटा प्रयोग गर्छौं, हामी मान्छौं कि सबै डेटा बिन्दुहरू केही सम्भाव्यता वितरणबाट लिइएका नमूनाहरू हुन्। यस मान्यताले हामीलाई मेसिन लर्निङ प्रविधिहरू लागू गर्न र कार्यशील भविष्यवाणी मोडेलहरू निर्माण गर्न अनुमति दिन्छ।

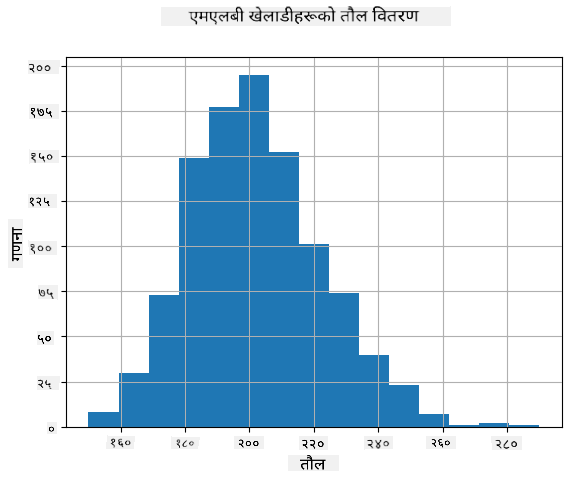
हाम्रो डेटाको वितरण कस्तो छ भनेर हेर्न, हामी हिस्टोग्राम नामक ग्राफ बनाउन सक्छौं। X-अक्षमा विभिन्न तौल अन्तरालहरूको संख्या (जसलाई बिन्स भनिन्छ) हुनेछ, र ठाडो अक्षमा हाम्रो र्‍यान्डम भेरिएबल नमूना कुनै दिइएको अन्तरालभित्र कति पटक थियो भन्ने देखाइनेछ।

यस हिस्टोग्रामबाट तपाईं देख्न सक्नुहुन्छ कि सबै मानहरू निश्चित औसत तौल वरिपरि केन्द्रित छन्, र औसतबाट जति टाढा जान्छौं - त्यति नै कम तौलका मानहरू भेटिन्छन्। अर्थात्, बेसबल खेलाडीको तौल औसत तौलभन्दा धेरै फरक हुने सम्भावना धेरै कम छ। तौलहरूको भिन्नताले तौलहरू औसतबाट कति फरक हुने सम्भावना छ भन्ने देखाउँछ।

यदि हामी बेसबल लिगका मानिसहरूबाहेक अरू मानिसहरूको तौल लिन्छौं भने, वितरण सम्भवतः फरक हुनेछ। तर, वितरणको आकार उस्तै हुनेछ, तर औसत र भिन्नता परिवर्तन हुनेछ। त्यसैले, यदि हामीले हाम्रो मोडेल बेसबल खेलाडीहरूमा प्रशिक्षण गर्यौं भने, यो विश्वविद्यालयका विद्यार्थीहरूमा लागू गर्दा गलत परिणाम दिन सक्छ, किनभने आधारभूत वितरण फरक छ।

नर्मल वितरण

हामीले माथि देखेको तौलको वितरण धेरै सामान्य हो, र वास्तविक जीवनका धेरै मापनहरू उस्तै प्रकारको वितरण अनुसरण गर्छन्, तर फरक औसत र भिन्नतासहित। यस वितरणलाई नर्मल वितरण भनिन्छ, र यो तथ्यांकमा धेरै महत्त्वपूर्ण भूमिका खेल्छ।

नर्मल वितरण प्रयोग गर्नु बेसबल खेलाडीहरूको सम्भावित तौलहरू उत्पन्न गर्ने सही तरिका हो। एक पटक हामीले औसत तौल mean र मानक विचलन std थाहा पाएपछि, हामी १००० तौल नमूनाहरू निम्न तरिकाले उत्पन्न गर्न सक्छौं:

samples = np.random.normal(mean,std,1000)

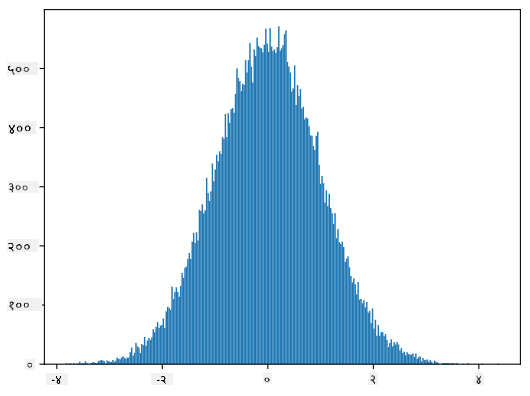
यदि हामी उत्पन्न नमूनाहरूको हिस्टोग्राम प्लट गर्छौं भने, हामीले माथि देखाइएको चित्रसँग धेरै मिल्दोजुल्दो चित्र देख्नेछौं। र यदि हामी नमूनाहरूको संख्या र बिन्सको संख्या बढाउँछौं भने, हामी आदर्शको नजिकको नर्मल वितरणको चित्र उत्पन्न गर्न सक्छौं:

औसत=0 र मानक विचलन=1 भएको नर्मल वितरण

विश्वास अन्तरालहरू

जब हामी बेसबल खेलाडीहरूको तौलको कुरा गर्छौं, हामी मान्छौं कि त्यहाँ निश्चित र्‍यान्डम भेरिएबल W छ, जसले सबै बेसबल खेलाडीहरूको तौलको आदर्श सम्भाव्यता वितरणलाई प्रतिनिधित्व गर्दछ (जसलाई जनसंख्या भनिन्छ)। हाम्रो तौलहरूको अनुक्रम सबै बेसबल खेलाडीहरूको उपसमूहसँग मेल खान्छ, जसलाई हामी नमूना भन्छौं। एउटा रोचक प्रश्न यो हो, के हामी W को वितरणका मापदण्डहरू, अर्थात् जनसंख्याको औसत र भिन्नता थाहा पाउन सक्छौं?

सबैभन्दा सजिलो उत्तर भनेको हाम्रो नमूनाको औसत र भिन्नता गणना गर्नु हो। तर, यस्तो हुन सक्छ कि हाम्रो र्‍यान्डम नमूनाले सम्पूर्ण जनसंख्यालाई सही रूपमा प्रतिनिधित्व गर्दैन। त्यसैले विश्वास अन्तराल को कुरा गर्नु उचित हुन्छ।

विश्वास अन्तराल भनेको हाम्रो नमुनाका आधारमा जनसंख्याको वास्तविक औसतको अनुमान हो, जुन निश्चित सम्भावना (वा विश्वासको स्तर) मा सही हुन्छ। मानौं हामीसँग हाम्रो वितरणबाट लिइएको नमूना X₁, ..., X_n छ। प्रत्येक पटक हामी हाम्रो वितरणबाट नमूना लिन्छौं, हामी फरक औसत मान μ पाउँछौं। त्यसैले μ लाई एक प्रकारको यादृच्छिक चर मान्न सकिन्छ। विश्वास अन्तराल (confidence interval) जसको विश्वास p छ, दुई मानहरूको जोडी (L_p,R_p) हो, जसले P(L_p≤μ≤R_p) = p सुनिश्चित गर्छ, अर्थात् औसत मान उक्त अन्तरालभित्र पर्ने सम्भावना p बराबर हुन्छ।

विश्वास अन्तराल कसरी गणना गरिन्छ भन्ने विस्तृत चर्चा हाम्रो छोटो परिचयको दायरा बाहिर जान्छ। थप विवरण विकिपिडिया मा भेट्न सकिन्छ। संक्षेपमा, हामी गणना गरिएको नमूना औसतको वितरणलाई जनसंख्याको वास्तविक औसतको सन्दर्भमा परिभाषित गर्छौं, जसलाई स्टुडेन्ट वितरण भनिन्छ।

रोचक तथ्य: स्टुडेन्ट वितरणको नाम गणितज्ञ विलियम सीली गोसेटको नाममा राखिएको हो, जसले आफ्नो कागज "स्टुडेन्ट" उपनाम अन्तर्गत प्रकाशित गरेका थिए। उनी गिनीज ब्रुअरीमा काम गर्थे, र एउटा कथन अनुसार, उनको नियोक्ताले कच्चा सामग्रीको गुणस्तर निर्धारण गर्न सांख्यिकीय परीक्षण प्रयोग गरिरहेको कुरा सार्वजनिकलाई थाहा होस् भन्ने चाहँदैनथे।

यदि हामी हाम्रो जनसंख्याको औसत μ लाई विश्वास p का साथ अनुमान गर्न चाहन्छौं भने, हामीलाई स्टुडेन्ट वितरण A को (1-p)/2-थ प्रतिशतक लिनुपर्छ, जुन तालिकाबाट लिइन सक्छ वा सांख्यिकीय सफ्टवेयर (जस्तै Python, R, आदि) को केही बिल्ट-इन फङ्सन प्रयोग गरेर गणना गर्न सकिन्छ। त्यसपछि μ को अन्तराल X±A*D/√n हुनेछ, जहाँ X नमूनाबाट प्राप्त औसत हो, D मानक विचलन हो।

नोट: हामी डिग्री अफ फ्रिडम को महत्त्वपूर्ण अवधारणाको चर्चा पनि छोड्छौं, जुन स्टुडेन्ट वितरणसँग सम्बन्धित छ। यस अवधारणालाई गहिरो रूपमा बुझ्नको लागि सांख्यिकीको थप पूर्ण पुस्तकहरू हेर्न सकिन्छ।

वजन र उचाइको विश्वास अन्तराल गणना गर्ने उदाहरण संग्लग्न नोटबुकहरू मा दिइएको छ।

p	वजन औसत
0.85	201.73±0.94
0.90	201.73±1.08
0.95	201.73±1.28

ध्यान दिनुहोस् कि विश्वास सम्भावना जति उच्च हुन्छ, विश्वास अन्तराल त्यति नै चौडा हुन्छ।

परिकल्पना परीक्षण

हाम्रो बेसबल खेलाडीहरूको डेटासेटमा विभिन्न खेलाडी भूमिकाहरू छन्, जसलाई तल संक्षेपमा प्रस्तुत गर्न सकिन्छ (यो तालिका कसरी गणना गर्न सकिन्छ भन्ने हेर्न संग्लग्न नोटबुक हेर्नुहोस्):

भूमिका	उचाइ	वजन	संख्या
क्याचर	72.723684	204.328947	76
डिजिनेटेड हिटर	74.222222	220.888889	18
फर्स्ट बेसम्यान	74.000000	213.109091	55
आउटफिल्डर	73.010309	199.113402	194
रिलिफ पिचर	74.374603	203.517460	315
सेकेन्ड बेसम्यान	71.362069	184.344828	58
शर्टस्टप	71.903846	182.923077	52
स्टार्टिङ पिचर	74.719457	205.163636	221
थर्ड बेसम्यान	73.044444	200.955556	45

हामी देख्न सक्छौं कि फर्स्ट बेसम्यानको औसत उचाइ सेकेन्ड बेसम्यानको भन्दा बढी छ। त्यसैले, हामी फर्स्ट बेसम्यान सेकेन्ड बेसम्यानभन्दा अग्लो हुन्छन् भन्ने निष्कर्ष निकाल्न चाहन सक्छौं।

यो कथनलाई परिकल्पना भनिन्छ, किनकि हामीलाई यो तथ्य वास्तवमा सत्य हो कि होइन भन्ने थाहा छैन।

तर, यो निष्कर्ष निकाल्न सकिन्छ कि सकिँदैन भन्ने कुरा सधैं स्पष्ट हुँदैन। माथिको छलफलबाट हामी जान्दछौं कि प्रत्येक औसतसँग सम्बन्धित विश्वास अन्तराल हुन्छ, र यो भिन्नता केवल सांख्यिकीय त्रुटि हुन सक्छ। हामीलाई हाम्रो परिकल्पनाको परीक्षण गर्न थप औपचारिक तरिका चाहिन्छ।

हामी फर्स्ट र सेकेन्ड बेसम्यानको उचाइको विश्वास अन्तराल अलग-अलग गणना गरौं:

विश्वास	फर्स्ट बेसम्यान	सेकेन्ड बेसम्यान
0.85	73.62..74.38	71.04..71.69
0.90	73.56..74.44	70.99..71.73
0.95	73.47..74.53	70.92..71.81

हामी देख्न सक्छौं कि कुनै पनि विश्वासमा अन्तरालहरू ओभरल्याप गर्दैनन्। यसले हाम्रो परिकल्पनालाई प्रमाणित गर्छ कि फर्स्ट बेसम्यान सेकेन्ड बेसम्यानभन्दा अग्लो हुन्छन्।

अझ औपचारिक रूपमा, हामीले समाधान गर्न खोजिरहेको समस्या भनेको दुई सम्भाव्यता वितरणहरू समान छन् कि छैनन्, वा कम्तीमा तिनीहरूको समान प्यारामिटरहरू छन्। वितरणको प्रकारको आधारमा, हामीले त्यसका लागि विभिन्न परीक्षणहरू प्रयोग गर्नुपर्छ। यदि हामीलाई थाहा छ कि हाम्रो वितरणहरू सामान्य छन्, हामी स्टुडेन्ट टि-टेस्ट लागू गर्न सक्छौं।

स्टुडेन्ट टि-टेस्टमा, हामी तथाकथित t-value गणना गर्छौं, जसले औसतहरू बीचको भिन्नता देखाउँछ, विचलनलाई ध्यानमा राख्दै। यो देखाइएको छ कि t-value स्टुडेन्ट वितरण अनुसरण गर्छ, जसले हामीलाई दिइएको विश्वास स्तर p को लागि थ्रेसहोल्ड मान प्राप्त गर्न अनुमति दिन्छ (यो गणना गर्न सकिन्छ, वा संख्यात्मक तालिकाहरूमा हेर्न सकिन्छ)। त्यसपछि हामी t-value लाई यो थ्रेसहोल्डसँग तुलना गर्छौं ताकि परिकल्पनालाई स्वीकृत वा अस्वीकृत गर्न सकियोस्।

Python मा, हामी SciPy प्याकेज प्रयोग गर्न सक्छौं, जसमा ttest_ind फङ्सन समावेश छ (थुप्रै अन्य उपयोगी सांख्यिकीय फङ्सनहरू सहित!)। यसले हाम्रो लागि t-value गणना गर्छ, र विश्वास p-value को रिभर्स लुकअप पनि गर्छ, ताकि हामी केवल विश्वासलाई हेरेर निष्कर्ष निकाल्न सकौं।

उदाहरणका लागि, फर्स्ट र सेकेन्ड बेसम्यानको उचाइको तुलना गर्दा हामीले निम्न परिणामहरू पाउँछौं:

from scipy.stats import ttest_ind

tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")

T-value = 7.65
P-value: 9.137321189738925e-12

हाम्रो केसमा, p-value धेरै कम छ, जसले फर्स्ट बेसम्यान अग्लो हुने बलियो प्रमाण देखाउँछ।

त्यहाँ अन्य विभिन्न प्रकारका परिकल्पनाहरू पनि छन् जुन हामी परीक्षण गर्न चाहन सक्छौं, जस्तै:

कुनै नमूना कुनै वितरण अनुसरण गर्छ भन्ने प्रमाणित गर्न। हाम्रो केसमा हामीले मान्य गरेका छौं कि उचाइ सामान्य रूपमा वितरण गरिएको छ, तर त्यसलाई औपचारिक सांख्यिकीय प्रमाण चाहिन्छ।
कुनै नमूनाको औसत मान कुनै पूर्वनिर्धारित मानसँग मेल खान्छ भन्ने प्रमाणित गर्न
विभिन्न नमूनाहरूको औसत तुलना गर्न (जस्तै, विभिन्न उमेर समूहहरू बीचको खुशी स्तरको भिन्नता के हो)

ठूलो संख्याको नियम र केन्द्रीय सीमा प्रमेय

सामान्य वितरण किन महत्त्वपूर्ण छ भन्ने कारणमध्ये एक केन्द्रीय सीमा प्रमेय हो। मानौं हामीसँग स्वतन्त्र N मानहरूको ठूलो नमूना X₁, ..., X_N छ, जुन कुनै पनि वितरणबाट औसत μ र विचलन σ² सहित लिइएको छ। त्यसपछि, पर्याप्त ठूलो N को लागि (अर्को शब्दमा, जब N→∞), औसत Σ_iX_i सामान्य रूपमा वितरण हुनेछ, औसत μ र विचलन σ²/N सहित।

केन्द्रीय सीमा प्रमेयलाई अर्को तरिकाले व्याख्या गर्न सकिन्छ कि कुनै पनि यादृच्छिक चर मानहरूको योगको औसत गणना गर्दा तपाईं सामान्य वितरणमा पुग्नुहुन्छ।

केन्द्रीय सीमा प्रमेयबाट यो पनि निष्कर्ष निकाल्न सकिन्छ कि, जब N→∞, नमूनाको औसत μ बराबर हुने सम्भावना 1 हुन्छ। यसलाई ठूलो संख्याको नियम भनिन्छ।

सहसंबंध र सहविचलन

डेटा विज्ञानले गर्ने काममध्ये एक भनेको डेटा बीचको सम्बन्ध पत्ता लगाउनु हो। हामी भन्छौं कि दुई क्रमहरू सहसंबद्ध छन् जब तिनीहरूले एकै समयमा समान व्यवहार देखाउँछन्, अर्थात् तिनीहरू एकसाथ बढ्छन्/घट्छन्, वा एउटा बढ्दा अर्को घट्छ र उल्टो। अर्को शब्दमा, दुई क्रमहरू बीच केही सम्बन्ध देखिन्छ।

सहसंबंधले दुई क्रमहरू बीचको कारणात्मक सम्बन्धलाई अनिवार्य रूपमा संकेत गर्दैन; कहिलेकाहीं दुवै चरहरू कुनै बाह्य कारणमा निर्भर हुन सक्छन्, वा यो केवल संयोगले दुई क्रमहरू सहसंबद्ध हुन सक्छ। तर, बलियो गणितीय सहसंबंधले दुई चरहरू कुनै न कुनै रूपमा जडान भएको राम्रो संकेत दिन्छ।

गणितीय रूपमा, दुई यादृच्छिक चरहरू बीचको सम्बन्ध देखाउने मुख्य अवधारणा सहविचलन हो, जुन यसरी गणना गरिन्छ: Cov(X,Y) = E[(X-E(X))(Y-E(Y))]। हामी दुवै चरहरूको औसत मानबाट विचलन गणना गर्छौं, र त्यस विचलनहरूको गुणनफल। यदि दुवै चरहरू सँगै विचलित हुन्छन्, गुणनफल सधैं सकारात्मक मान हुनेछ, जसले सकारात्मक सहविचलनमा जोड दिनेछ। यदि दुवै चरहरू असंगत रूपमा विचलित हुन्छन् (अर्थात् एउटा औसतभन्दा तल झर्दा अर्को औसतभन्दा माथि बढ्छ), हामी सधैं नकारात्मक संख्याहरू पाउँछौं, जसले नकारात्मक सहविचलनमा जोड दिनेछ। यदि विचलनहरू निर्भर छैनन्, तिनीहरू लगभग शून्यमा जोडिनेछन्।

सहविचलनको पूर्ण मानले सहसंबंध कति ठूलो छ भन्ने धेरै कुरा बताउँदैन, किनकि यो वास्तविक मानहरूको परिमाणमा निर्भर गर्दछ। यसलाई सामान्यीकरण गर्न, हामी दुवै चरहरूको मानक विचलनद्वारा सहविचलनलाई विभाजन गर्न सक्छौं, जसले सहसंबंध दिन्छ। राम्रो कुरा यो हो कि सहसंबंध सधैं [-1,1] को दायरामा हुन्छ, जहाँ 1 ले मानहरू बीचको बलियो सकारात्मक सहसंबंध संकेत गर्दछ, -1 - बलियो नकारात्मक सहसंबंध, र 0 - कुनै सहसंबंध छैन (चरहरू स्वतन्त्र छन्)।

उदाहरण: हामी बेसबल खेलाडीहरूको वजन र उचाइ बीचको सहसंबंध गणना गर्न सक्छौं:

print(np.corrcoef(weights,heights))

यसको परिणामस्वरूप, हामी यस्तो सहसंबंध म्याट्रिक्स पाउँछौं:

array([[1.        , 0.52959196],
       [0.52959196, 1.        ]])

सहसंबंध म्याट्रिक्स C कुनै पनि संख्याको इनपुट क्रमहरू S₁, ..., S_n को लागि गणना गर्न सकिन्छ। C_ij को मान S_i र S_j बीचको सहसंबंध हो, र कर्ण तत्वहरू सधैं 1 हुन्छन् (जसलाई S_i को आत्म-सहसंबंध पनि भनिन्छ)।

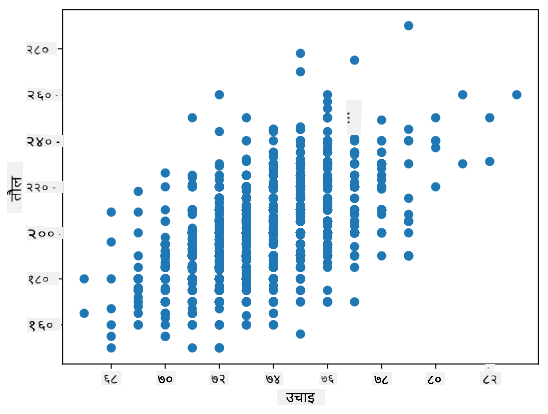
हाम्रो केसमा, मान 0.53 ले व्यक्तिको वजन र उचाइ बीच केही सहसंबंध रहेको संकेत गर्दछ। हामी एक मानलाई अर्कोको विरुद्धमा स्क्याटर प्लट बनाउन सक्छौं ताकि सम्बन्धलाई दृश्य रूपमा देख्न सकियोस्:

सहसंबंध र सहविचलनका थप उदाहरणहरू संग्लग्न नोटबुक मा भेट्न सकिन्छ।

निष्कर्ष

यस खण्डमा, हामीले सिक्यौं:

डेटा, जस्तै औसत, विचलन, मोड र क्वार्टाइलहरूको आधारभूत सांख्यिकीय गुणहरू
यादृच्छिक चरहरूको विभिन्न वितरणहरू, जसमा सामान्य वितरण समावेश छ
विभिन्न गुणहरू बीचको सहसंबंध कसरी पत्ता लगाउने
केही परिकल्पनाहरू प्रमाणित गर्न गणित र सांख्यिकीको साउन्ड उपकरण कसरी प्रयोग गर्ने
डेटा नमूनाको आधारमा यादृच्छिक चरको विश्वास अन्तराल कसरी गणना गर्ने

यद्यपि यो सम्भाव्यता र सांख्यिकीभित्रका विषयहरूको पूर्ण सूची होइन, यो तपाईंलाई यस पाठ्यक्रममा राम्रो सुरुवात दिन पर्याप्त हुनुपर्छ।

🚀 चुनौती

नोटबुकमा रहेको नमूना कोड प्रयोग गरेर अन्य परिकल्पनाहरू परीक्षण गर्नुहोस्:

फर्स्ट बेसम्यान सेकेन्ड बेसम्यानभन्दा पुराना छन्
फर्स्ट बेसम्यान थर्ड बेसम्यानभन्दा अग्लो छन्
शर्टस्टप सेकेन्ड बेसम्यानभन्दा अग्लो छन्

पाठपश्चात क्विज

समीक्षा र आत्म अध्ययन

संभाव्यता र सांख्यिकी यति व्यापक विषय हो कि यसले आफ्नै पाठ्यक्रमको हकदार छ। यदि तपाईं सिद्धान्तमा गहिरो जान इच्छुक हुनुहुन्छ भने, तपाईं निम्न पुस्तकहरू पढ्न जारी राख्न चाहनुहुन्छ:

न्यूयोर्क विश्वविद्यालयका कार्लोस फर्नान्डेज-ग्रान्डा का उत्कृष्ट व्याख्यान नोटहरू Probability and Statistics for Data Science (अनलाइन उपलब्ध)
पिटर र एन्ड्रु ब्रुस। Practical Statistics for Data Scientists. [R मा नमूना कोड]।
जेम्स डी. मिलर। Statistics for Data Science [R मा नमूना कोड]।

असाइनमेन्ट

सानो मधुमेह अध्ययन

श्रेय

यो पाठ दिमित्री सोश्निकोभ द्वारा ♥️ सहित लेखिएको हो।

अस्वीकरण:
यो दस्तावेज़ AI अनुवाद सेवा Co-op Translator प्रयोग गरेर अनुवाद गरिएको छ। हामी शुद्धताको लागि प्रयास गर्छौं, तर कृपया ध्यान दिनुहोस् कि स्वचालित अनुवादहरूमा त्रुटि वा अशुद्धता हुन सक्छ। यसको मूल भाषा मा रहेको मूल दस्तावेज़लाई आधिकारिक स्रोत मानिनुपर्छ। महत्वपूर्ण जानकारीको लागि, व्यावसायिक मानव अनुवाद सिफारिस गरिन्छ। यस अनुवादको प्रयोगबाट उत्पन्न हुने कुनै पनि गलतफहमी वा गलत व्याख्याको लागि हामी जिम्मेवार हुने छैनौं।

README.md Unescape Escape