# सांख्यिकी और संभाव्यता का संक्षिप्त परिचय
| ](../../sketchnotes/04-Statistics-Probability.png)|
|:---:|
| सांख्यिकी और संभाव्यता - _Sketchnote by [@nitya](https://twitter.com/nitya)_ |
सांख्यिकी और संभाव्यता सिद्धांत गणित के दो अत्यधिक संबंधित क्षेत्र हैं जो डेटा विज्ञान के लिए बहुत प्रासंगिक हैं। गणित का गहन ज्ञान न होने पर भी डेटा के साथ काम करना संभव है, लेकिन कुछ बुनियादी अवधारणाओं को जानना हमेशा बेहतर होता है। यहां हम एक छोटा सा परिचय प्रस्तुत करेंगे जो आपको शुरुआत करने में मदद करेगा।
[](https://youtu.be/Z5Zy85g4Yjw)
## [पूर्व-व्याख्यान क्विज़](https://ff-quizzes.netlify.app/en/ds/quiz/6)
## संभाव्यता और रैंडम वेरिएबल्स
**संभाव्यता** 0 और 1 के बीच की एक संख्या है जो किसी **घटना** के होने की संभावना को व्यक्त करती है। इसे सकारात्मक परिणामों की संख्या (जो घटना की ओर ले जाते हैं) को कुल परिणामों की संख्या से विभाजित करके परिभाषित किया जाता है, यह मानते हुए कि सभी परिणाम समान रूप से संभावित हैं। उदाहरण के लिए, जब हम एक पासा फेंकते हैं, तो एक सम संख्या प्राप्त करने की संभावना 3/6 = 0.5 है।
जब हम घटनाओं के बारे में बात करते हैं, तो हम **रैंडम वेरिएबल्स** का उपयोग करते हैं। उदाहरण के लिए, पासा फेंकने पर प्राप्त संख्या का प्रतिनिधित्व करने वाला रैंडम वेरिएबल 1 से 6 तक के मान लेगा। 1 से 6 तक की संख्या का सेट **सैंपल स्पेस** कहलाता है। हम रैंडम वेरिएबल के किसी निश्चित मान लेने की संभावना के बारे में बात कर सकते हैं, जैसे P(X=3)=1/6।
पिछले उदाहरण में रैंडम वेरिएबल को **डिस्क्रीट** कहा जाता है, क्योंकि इसका सैंपल स्पेस गिनने योग्य है, यानी अलग-अलग मान हैं जिन्हें सूचीबद्ध किया जा सकता है। ऐसे मामले भी होते हैं जब सैंपल स्पेस वास्तविक संख्याओं की एक सीमा या पूरे वास्तविक संख्याओं का सेट होता है। ऐसे वेरिएबल्स को **कंटीन्यस** कहा जाता है। एक अच्छा उदाहरण है बस के आने का समय।
## संभाव्यता वितरण
डिस्क्रीट रैंडम वेरिएबल्स के मामले में, प्रत्येक घटना की संभावना को एक फ़ंक्शन P(X) द्वारा वर्णित करना आसान है। सैंपल स्पेस *S* से प्रत्येक मान *s* के लिए यह 0 से 1 तक की संख्या देगा, ताकि सभी घटनाओं के लिए P(X=s) के सभी मानों का योग 1 हो।
सबसे प्रसिद्ध डिस्क्रीट वितरण **यूनिफॉर्म वितरण** है, जिसमें N तत्वों का सैंपल स्पेस होता है, और प्रत्येक के लिए समान संभावना 1/N होती है।
कंटीन्यस वेरिएबल के संभाव्यता वितरण का वर्णन करना अधिक कठिन है, जिसमें मान [a,b] के कुछ अंतराल से या पूरे वास्तविक संख्याओं ℝ से लिए जाते हैं। बस के आने के समय के मामले पर विचार करें। वास्तव में, प्रत्येक सटीक समय *t* के लिए, बस के ठीक उसी समय आने की संभावना 0 है!
> अब आप जानते हैं कि 0 संभावना वाली घटनाएं होती हैं, और बहुत बार होती हैं! कम से कम हर बार जब बस आती है!
हम केवल वेरिएबल के किसी दिए गए मानों के अंतराल में गिरने की संभावना के बारे में बात कर सकते हैं, जैसे P(t1≤X2)। इस मामले में, संभाव्यता वितरण को **संभाव्यता घनत्व फ़ंक्शन** p(x) द्वारा वर्णित किया जाता है, ताकि
 यहां हम **इंटर-क्वारटाइल रेंज** IQR=Q3-Q1 और तथाकथित **आउटलायर्स** - मान जो [Q1-1.5*IQR,Q3+1.5*IQR] की सीमाओं के बाहर होते हैं, की भी गणना करते हैं।
एक सीमित वितरण जिसमें संभावित मानों की संख्या कम होती है, एक अच्छा "विशिष्ट" मान वह होता है जो सबसे अधिक बार प्रकट होता है, जिसे **मोड** कहा जाता है। इसे अक्सर श्रेणीबद्ध डेटा, जैसे रंगों, पर लागू किया जाता है। मान लें कि हमारे पास दो समूह हैं - कुछ जो लाल रंग को पसंद करते हैं और अन्य जो नीले रंग को पसंद करते हैं। यदि हम रंगों को संख्याओं द्वारा कोड करते हैं, तो पसंदीदा रंग के लिए माध्य मान कहीं नारंगी-हरे स्पेक्ट्रम में होगा, जो किसी भी समूह की वास्तविक प्राथमिकता को इंगित नहीं करता। हालांकि, मोड या तो एक रंग होगा, या दोनों रंग होंगे, यदि उनके लिए मतदान करने वाले लोगों की संख्या समान है (इस मामले में हम नमूने को **मल्टीमोडल** कहते हैं)।
## वास्तविक दुनिया का डेटा
जब हम वास्तविक जीवन के डेटा का विश्लेषण करते हैं, तो वे अक्सर रैंडम वेरिएबल्स के रूप में नहीं होते हैं, इस अर्थ में कि हम अज्ञात परिणामों के साथ प्रयोग नहीं करते। उदाहरण के लिए, बेसबॉल खिलाड़ियों की एक टीम पर विचार करें, और उनके शरीर के डेटा, जैसे ऊंचाई, वजन और उम्र। ये संख्याएं बिल्कुल रैंडम नहीं हैं, लेकिन हम अभी भी उन्हीं गणितीय अवधारणाओं को लागू कर सकते हैं। उदाहरण के लिए, लोगों के वजन का अनुक्रम कुछ रैंडम वेरिएबल से लिए गए मानों का अनुक्रम माना जा सकता है। नीचे [मेजर लीग बेसबॉल](http://mlb.mlb.com/index.jsp) के वास्तविक बेसबॉल खिलाड़ियों के वजन का अनुक्रम दिया गया है, जो [इस डेटासेट](http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_MLB_HeightsWeights) से लिया गया है (आपकी सुविधा के लिए केवल पहले 20 मान दिखाए गए हैं):
```
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
```
> **नोट**: इस डेटासेट के साथ काम करने के उदाहरण को देखने के लिए, [संबंधित नोटबुक](notebook.ipynb) देखें। इस पाठ में कई चुनौतियां भी हैं, और आप उस नोटबुक में कुछ कोड जोड़कर उन्हें पूरा कर सकते हैं। यदि आप डेटा पर काम करने के तरीके के बारे में सुनिश्चित नहीं हैं, तो चिंता न करें - हम बाद में Python का उपयोग करके डेटा पर काम करने पर वापस आएंगे। यदि आप Jupyter Notebook में कोड चलाने का तरीका नहीं जानते हैं, तो [इस लेख](https://soshnikov.com/education/how-to-execute-notebooks-from-github/) को देखें।
यहां हमारे डेटा के लिए माध्य, माध्यिका और क्वारटाइल्स दिखाने वाला बॉक्स प्लॉट है:
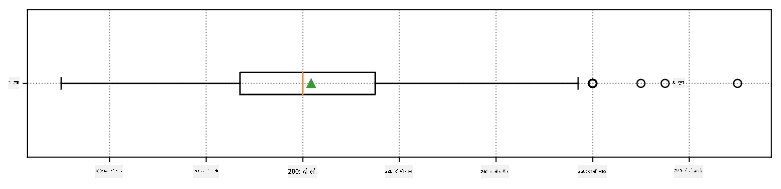
चूंकि हमारे डेटा में विभिन्न खिलाड़ी **भूमिकाओं** की जानकारी है, हम भूमिका के अनुसार भी बॉक्स प्लॉट बना सकते हैं - यह हमें यह विचार करने की अनुमति देगा कि भूमिकाओं के बीच पैरामीटर मान कैसे भिन्न होते हैं। इस बार हम ऊंचाई पर विचार करेंगे:
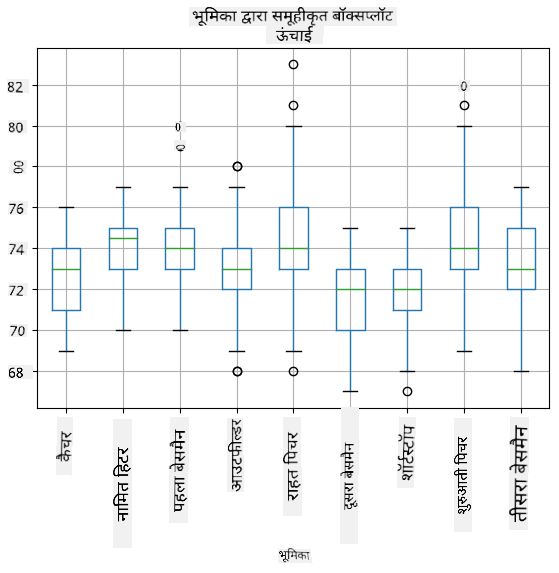
यह आरेख सुझाव देता है कि, औसतन, पहले बेसमैन की ऊंचाई दूसरे बेसमैन की ऊंचाई से अधिक है। इस पाठ में बाद में हम सीखेंगे कि इस परिकल्पना को अधिक औपचारिक रूप से कैसे परीक्षण किया जा सकता है, और यह प्रदर्शित करने के लिए कि हमारे डेटा सांख्यिकीय रूप से महत्वपूर्ण है।
> जब वास्तविक दुनिया के डेटा के साथ काम करते हैं, तो हम मानते हैं कि सभी डेटा पॉइंट्स कुछ संभाव्यता वितरण से लिए गए नमूने हैं। यह धारणा हमें मशीन लर्निंग तकनीकों को लागू करने और काम करने वाले भविष्यवाणी मॉडल बनाने की अनुमति देती है।
हमारे डेटा का वितरण कैसा है, यह देखने के लिए हम **हिस्टोग्राम** नामक एक ग्राफ़ बना सकते हैं। X-अक्ष में विभिन्न वजन अंतराल (जिसे **बिन्स** कहा जाता है) की संख्या होगी, और वर्टिकल अक्ष दिखाएगा कि हमारा रैंडम वेरिएबल नमूना दिए गए अंतराल में कितनी बार था।
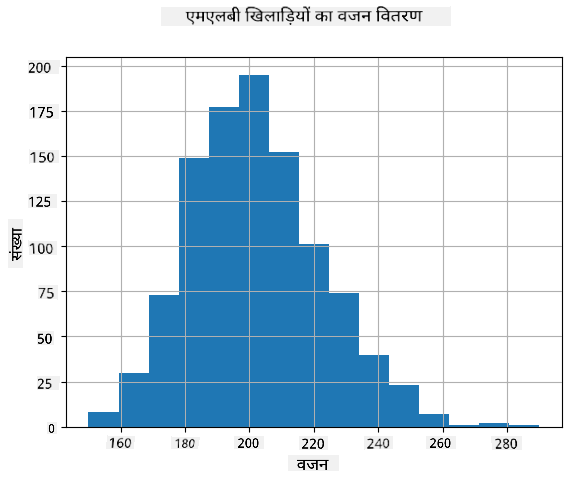
इस हिस्टोग्राम से आप देख सकते हैं कि सभी मान एक निश्चित माध्य वजन के आसपास केंद्रित हैं, और जैसे-जैसे हम उस वजन से दूर जाते हैं - उस मान के वजन कम बार मिलते हैं। यानी, यह बहुत ही असंभावित है कि बेसबॉल खिलाड़ी का वजन माध्य वजन से बहुत अलग होगा। वजन का विचरण दिखाता है कि वजन माध्य से कितना भिन्न होने की संभावना है।
> यदि हम अन्य लोगों के वजन लेते हैं, जो बेसबॉल लीग से नहीं हैं, तो वितरण अलग होने की संभावना है। हालांकि, वितरण का आकार समान रहेगा, लेकिन माध्य और विचरण बदल जाएंगे। इसलिए, यदि हम अपने मॉडल को बेसबॉल खिलाड़ियों पर प्रशिक्षित करते हैं, तो यह विश्वविद्यालय के छात्रों पर लागू होने पर गलत परिणाम देने की संभावना है, क्योंकि अंतर्निहित वितरण अलग है।
## नॉर्मल वितरण
ऊपर हमने जो वजन का वितरण देखा वह बहुत सामान्य है, और वास्तविक दुनिया से कई माप एक ही प्रकार के वितरण का पालन करते हैं, लेकिन अलग-अलग माध्य और विचरण के साथ। इस वितरण को **नॉर्मल वितरण** कहा जाता है, और यह सांख्यिकी में बहुत महत्वपूर्ण भूमिका निभाता है।
नॉर्मल वितरण का उपयोग संभावित बेसबॉल खिलाड़ियों के रैंडम वजन उत्पन्न करने का सही तरीका है। एक बार जब हम माध्य वजन `mean` और मानक विचलन `std` जानते हैं, तो हम निम्नलिखित तरीके से 1000 वजन नमूने उत्पन्न कर सकते हैं:
```python
samples = np.random.normal(mean,std,1000)
```
यदि हम उत्पन्न नमूनों का हिस्टोग्राम बनाते हैं, तो हम ऊपर दिखाए गए चित्र के समान चित्र देखेंगे। और यदि हम नमूनों की संख्या और बिन्स की संख्या बढ़ाते हैं, तो हम नॉर्मल वितरण की एक अधिक आदर्श तस्वीर उत्पन्न कर सकते हैं:
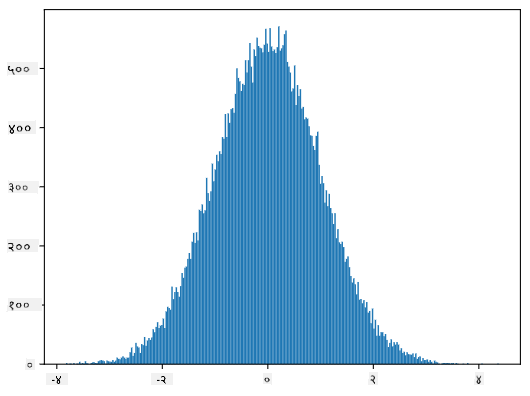
*माध्य=0 और मानक विचलन=1 के साथ नॉर्मल वितरण*
## विश्वास अंतराल
जब हम बेसबॉल खिलाड़ियों के वजन के बारे में बात करते हैं, तो हम मानते हैं कि एक निश्चित **रैंडम वेरिएबल W** है जो सभी बेसबॉल खिलाड़ियों के वजन के आदर्श संभाव्यता वितरण (जिसे **जनसंख्या** कहा जाता है) से मेल खाता है। हमारे वजन का अनुक्रम सभी बेसबॉल खिलाड़ियों के एक उपसमुच्चय से मेल खाता है जिसे हम **नमूना** कहते हैं। एक दिलचस्प सवाल यह है कि क्या हम W के वितरण के पैरामीटर, यानी जनसंख्या के माध्य और विचरण को जान सकते हैं?
सबसे आसान उत्तर होगा हमारे नमूने के माध्य और विचरण की गणना करना। हालांकि, ऐसा हो सकता है कि हमारा रैंडम नमूना पूरी जनसंख्या का सटीक प्रतिनिधित्व न करे। इसलिए **विश्वास अंतराल** के बारे में बात करना समझ में आता है।
> **विश्वास अंतराल** हमारे नमूने को देखते हुए जनसंख्या के वास्तविक माध्य का अनुमान है, जो एक निश्चित संभावना (या **विश्वास स्तर**) में सटीक है।
मान लें कि हमारे पास एक नमूना X
1, ..., Xn को हमारे वितरण से चुना गया है। हर बार जब हम अपने वितरण से एक नमूना लेते हैं, तो हमें अलग-अलग औसत मान μ प्राप्त होगा। इसलिए μ को एक यादृच्छिक चर माना जा सकता है। एक **विश्वास अंतराल** (confidence interval) जिसमें विश्वास p है, वह दो मानों (Lp,Rp) का एक युग्म है, ऐसा कि **P**(Lp≤μ≤Rp) = p, यानी मापा गया औसत मान इस अंतराल में आने की संभावना p के बराबर है।
यह हमारी छोटी सी भूमिका से परे है कि हम विस्तार से चर्चा करें कि इन विश्वास अंतरालों की गणना कैसे की जाती है। कुछ और विवरण [विकिपीडिया](https://en.wikipedia.org/wiki/Confidence_interval) पर पाए जा सकते हैं। संक्षेप में, हम वास्तविक जनसंख्या औसत के सापेक्ष गणना किए गए नमूना औसत के वितरण को परिभाषित करते हैं, जिसे **स्टूडेंट वितरण** (student distribution) कहा जाता है।
> **रोचक तथ्य**: स्टूडेंट वितरण का नाम गणितज्ञ विलियम सीली गॉसेट के नाम पर रखा गया है, जिन्होंने "स्टूडेंट" उपनाम के तहत अपना पेपर प्रकाशित किया। वे गिनीज ब्रुअरी में काम करते थे, और एक संस्करण के अनुसार, उनके नियोक्ता नहीं चाहते थे कि आम जनता को पता चले कि वे कच्चे माल की गुणवत्ता निर्धारित करने के लिए सांख्यिकीय परीक्षणों का उपयोग कर रहे थे।
यदि हम अपनी जनसंख्या के औसत μ का p विश्वास के साथ अनुमान लगाना चाहते हैं, तो हमें स्टूडेंट वितरण A का *(1-p)/2-थ परसेंटाइल* लेना होगा, जिसे या तो तालिकाओं से लिया जा सकता है, या सांख्यिकीय सॉफ़्टवेयर (जैसे Python, R, आदि) के कुछ अंतर्निर्मित कार्यों का उपयोग करके कंप्यूटर पर गणना की जा सकती है। फिर μ के लिए अंतराल X±A*D/√n होगा, जहां X नमूने का प्राप्त औसत है, और D मानक विचलन है।
> **ध्यान दें**: हम [स्वतंत्रता की डिग्री](https://en.wikipedia.org/wiki/Degrees_of_freedom_(statistics)) की एक महत्वपूर्ण अवधारणा की चर्चा को भी छोड़ देते हैं, जो स्टूडेंट वितरण के संदर्भ में महत्वपूर्ण है। इस अवधारणा को गहराई से समझने के लिए आप सांख्यिकी पर अधिक पूर्ण पुस्तकों का संदर्भ ले सकते हैं।
वज़न और ऊंचाई के लिए विश्वास अंतराल की गणना का एक उदाहरण [संबंधित नोटबुक](notebook.ipynb) में दिया गया है।
| p | वज़न औसत |
|-----|-----------|
| 0.85 | 201.73±0.94 |
| 0.90 | 201.73±1.08 |
| 0.95 | 201.73±1.28 |
ध्यान दें कि विश्वास संभावना जितनी अधिक होती है, विश्वास अंतराल उतना ही चौड़ा होता है।
## परिकल्पना परीक्षण
हमारे बेसबॉल खिलाड़ियों के डेटासेट में, विभिन्न खिलाड़ी भूमिकाएँ हैं, जिन्हें नीचे सारांशित किया जा सकता है (कैसे यह तालिका गणना की गई है, यह देखने के लिए [संबंधित नोटबुक](notebook.ipynb) देखें):
| भूमिका | ऊंचाई | वज़न | संख्या |
|------|--------|--------|-------|
| कैचर | 72.723684 | 204.328947 | 76 |
| डिज़िग्नेटेड हिटर | 74.222222 | 220.888889 | 18 |
| फर्स्ट बेसमैन | 74.000000 | 213.109091 | 55 |
| आउटफील्डर | 73.010309 | 199.113402 | 194 |
| रिलीफ पिचर | 74.374603 | 203.517460 | 315 |
| सेकंड बेसमैन | 71.362069 | 184.344828 | 58 |
| शॉर्टस्टॉप | 71.903846 | 182.923077 | 52 |
| स्टार्टिंग पिचर | 74.719457 | 205.163636 | 221 |
| थर्ड बेसमैन | 73.044444 | 200.955556 | 45 |
हम देख सकते हैं कि फर्स्ट बेसमैन की औसत ऊंचाई सेकंड बेसमैन से अधिक है। इसलिए, हम यह निष्कर्ष निकालने के लिए प्रेरित हो सकते हैं कि **फर्स्ट बेसमैन सेकंड बेसमैन से ऊंचे होते हैं**।
> इस कथन को **एक परिकल्पना** कहा जाता है, क्योंकि हमें नहीं पता कि यह तथ्य वास्तव में सत्य है या नहीं।
हालांकि, यह हमेशा स्पष्ट नहीं होता कि हम यह निष्कर्ष निकाल सकते हैं या नहीं। ऊपर की चर्चा से हमें पता है कि प्रत्येक औसत का एक संबंधित विश्वास अंतराल होता है, और इसलिए यह अंतर केवल एक सांख्यिकीय त्रुटि हो सकता है। हमें अपनी परिकल्पना का परीक्षण करने के लिए कुछ अधिक औपचारिक तरीके की आवश्यकता है।
आइए फर्स्ट और सेकंड बेसमैन की ऊंचाई के लिए विश्वास अंतराल को अलग-अलग गणना करें:
| विश्वास | फर्स्ट बेसमैन | सेकंड बेसमैन |
|------------|---------------|----------------|
| 0.85 | 73.62..74.38 | 71.04..71.69 |
| 0.90 | 73.56..74.44 | 70.99..71.73 |
| 0.95 | 73.47..74.53 | 70.92..71.81 |
हम देख सकते हैं कि किसी भी विश्वास स्तर पर अंतराल ओवरलैप नहीं करते। यह हमारी परिकल्पना को साबित करता है कि फर्स्ट बेसमैन सेकंड बेसमैन से ऊंचे होते हैं।
औपचारिक रूप से, हम जो समस्या हल कर रहे हैं वह यह देखना है कि **दो संभाव्यता वितरण समान हैं या नहीं**, या कम से कम उनके मापदंड समान हैं। वितरण के आधार पर, हमें इसके लिए अलग-अलग परीक्षणों का उपयोग करना होगा। यदि हमें पता है कि हमारे वितरण सामान्य हैं, तो हम **[स्टूडेंट t-परीक्षण](https://en.wikipedia.org/wiki/Student%27s_t-test)** लागू कर सकते हैं।
स्टूडेंट t-परीक्षण में, हम तथाकथित **t-मूल्य** की गणना करते हैं, जो औसतों के बीच के अंतर को, विचलन को ध्यान में रखते हुए, इंगित करता है। यह प्रदर्शित किया गया है कि t-मूल्य **स्टूडेंट वितरण** का अनुसरण करता है, जो हमें दिए गए विश्वास स्तर **p** के लिए सीमा मान प्राप्त करने की अनुमति देता है (यह गणना की जा सकती है, या संख्यात्मक तालिकाओं में देखा जा सकता है)। फिर हम t-मूल्य की तुलना इस सीमा से करते हैं ताकि परिकल्पना को स्वीकार या अस्वीकार कर सकें।
Python में, हम **SciPy** पैकेज का उपयोग कर सकते हैं, जिसमें `ttest_ind` फ़ंक्शन शामिल है (साथ ही कई अन्य उपयोगी सांख्यिकीय फ़ंक्शन!)। यह हमारे लिए t-मूल्य की गणना करता है, और विश्वास p-मूल्य का रिवर्स लुकअप भी करता है, ताकि हम केवल विश्वास को देखकर निष्कर्ष निकाल सकें।
उदाहरण के लिए, फर्स्ट और सेकंड बेसमैन की ऊंचाई की तुलना हमें निम्नलिखित परिणाम देती है:
```python
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
```
```
T-value = 7.65
P-value: 9.137321189738925e-12
```
हमारे मामले में, p-मूल्य बहुत कम है, जिसका अर्थ है कि फर्स्ट बेसमैन के ऊंचे होने का मजबूत प्रमाण है।
इसके अलावा, अन्य प्रकार की परिकल्पनाएँ भी हो सकती हैं जिन्हें हम परीक्षण करना चाह सकते हैं, जैसे:
* यह साबित करना कि कोई दिया गया नमूना किसी वितरण का अनुसरण करता है। हमारे मामले में हमने मान लिया है कि ऊंचाई सामान्य रूप से वितरित है, लेकिन इसे औपचारिक सांख्यिकीय सत्यापन की आवश्यकता है।
* यह साबित करना कि किसी नमूने का औसत मान किसी पूर्वनिर्धारित मान से मेल खाता है।
* कई नमूनों के औसतों की तुलना करना (जैसे, विभिन्न आयु समूहों में खुशी के स्तर में क्या अंतर है)।
## बड़े संख्याओं का नियम और केंद्रीय सीमा प्रमेय
सामान्य वितरण इतना महत्वपूर्ण क्यों है, इसका एक कारण **केंद्रीय सीमा प्रमेय** (central limit theorem) है। मान लें कि हमारे पास स्वतंत्र N मानों X1, ..., XN का एक बड़ा नमूना है, जिसे किसी भी वितरण से लिया गया है, जिसका औसत μ और विचरण σ2 है। फिर, पर्याप्त बड़े N के लिए (दूसरे शब्दों में, जब N→∞), ΣiXi का औसत सामान्य रूप से वितरित होगा, जिसका औसत μ और विचरण σ2/N होगा।
> केंद्रीय सीमा प्रमेय की एक और व्याख्या यह है कि यह कहता है कि किसी भी यादृच्छिक चर मानों के योग का औसत निकालने पर आप सामान्य वितरण प्राप्त करते हैं।
केंद्रीय सीमा प्रमेय से यह भी पता चलता है कि, जब N→∞, नमूना औसत के μ के बराबर होने की संभावना 1 हो जाती है। इसे **बड़े संख्याओं का नियम** (law of large numbers) कहा जाता है।
## सहसंबंध और सहभिन्नता
डेटा साइंस का एक काम डेटा के बीच संबंध खोजना है। हम कहते हैं कि दो अनुक्रम **सहसंबद्ध** (correlate) हैं जब वे एक ही समय में समान व्यवहार प्रदर्शित करते हैं, यानी वे या तो एक साथ बढ़ते/घटते हैं, या एक अनुक्रम बढ़ता है जब दूसरा घटता है और इसके विपरीत। दूसरे शब्दों में, ऐसा लगता है कि दो अनुक्रमों के बीच कुछ संबंध है।
> सहसंबंध जरूरी नहीं कि दो अनुक्रमों के बीच कारणात्मक संबंध को इंगित करता है; कभी-कभी दोनों चर किसी बाहरी कारण पर निर्भर हो सकते हैं, या यह केवल संयोग से हो सकता है कि दोनों अनुक्रम सहसंबद्ध हैं। हालांकि, मजबूत गणितीय सहसंबंध इस बात का अच्छा संकेत है कि दो चर किसी न किसी तरह से जुड़े हुए हैं।
गणितीय रूप से, दो यादृच्छिक चरों के बीच संबंध दिखाने वाली मुख्य अवधारणा **सहभिन्नता** (covariance) है, जिसे इस प्रकार गणना किया जाता है: Cov(X,Y) = **E**\[(X-**E**(X))(Y-**E**(Y))\]। हम दोनों चरों के उनके औसत मानों से विचलन की गणना करते हैं, और फिर उन विचलनों के गुणनफल को लेते हैं। यदि दोनों चर एक साथ विचलित होते हैं, तो गुणनफल हमेशा एक सकारात्मक मान होगा, जो सकारात्मक सहभिन्नता में जुड़ जाएगा। यदि दोनों चर असंगत रूप से विचलित होते हैं (यानी एक औसत से नीचे गिरता है जब दूसरा औसत से ऊपर उठता है), तो हमें हमेशा नकारात्मक संख्याएँ मिलेंगी, जो नकारात्मक सहभिन्नता में जुड़ेंगी। यदि विचलन स्वतंत्र हैं, तो वे लगभग शून्य में जुड़ेंगे।
सहभिन्नता का परिमाण हमें यह नहीं बताता कि सहसंबंध कितना बड़ा है, क्योंकि यह वास्तविक मानों के परिमाण पर निर्भर करता है। इसे सामान्यीकृत करने के लिए, हम सहभिन्नता को दोनों चरों के मानक विचलन से विभाजित कर सकते हैं, ताकि **सहसंबंध** प्राप्त हो। अच्छी बात यह है कि सहसंबंध हमेशा [-1,1] की सीमा में होता है, जहां 1 मानों के बीच मजबूत सकारात्मक सहसंबंध को इंगित करता है, -1 - मजबूत नकारात्मक सहसंबंध, और 0 - बिल्कुल भी सहसंबंध नहीं (चर स्वतंत्र हैं)।
**उदाहरण**: हम ऊपर उल्लिखित बेसबॉल खिलाड़ियों के डेटासेट से वज़न और ऊंचाई के बीच सहसंबंध की गणना कर सकते हैं:
```python
print(np.corrcoef(weights,heights))
```
परिणामस्वरूप, हमें इस प्रकार का **सहसंबंध मैट्रिक्स** मिलता है:
```
array([[1. , 0.52959196],
[0.52959196, 1. ]])
```
> सहसंबंध मैट्रिक्स C किसी भी संख्या के इनपुट अनुक्रमों S1, ..., Sn के लिए गणना की जा सकती है। Cij का मान Si और Sj के बीच सहसंबंध है, और विकर्ण तत्व हमेशा 1 होते हैं (जो Si का आत्म-सहसंबंध भी है)।
हमारे मामले में, मान 0.53 इंगित करता है कि किसी व्यक्ति के वज़न और ऊंचाई के बीच कुछ सहसंबंध है। हम एक मान को दूसरे के खिलाफ बिखराव प्लॉट भी बना सकते हैं ताकि संबंध को दृश्य रूप से देखा जा सके:
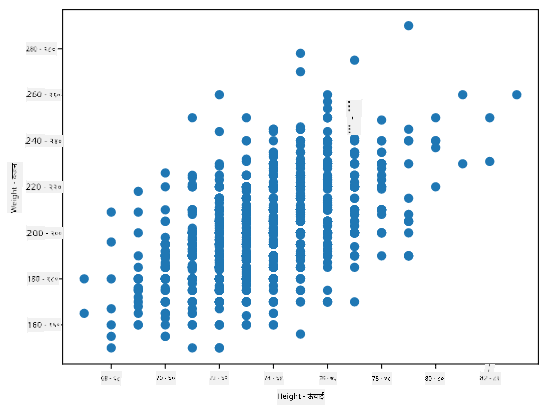
> सहसंबंध और सहभिन्नता के और उदाहरण [संबंधित नोटबुक](notebook.ipynb) में पाए जा सकते हैं।
## निष्कर्ष
इस खंड में, हमने सीखा:
* डेटा के बुनियादी सांख्यिकीय गुण, जैसे औसत, विचरण, माध्यिका और चतुर्थांश
* यादृच्छिक चरों के विभिन्न वितरण, जिसमें सामान्य वितरण शामिल है
* विभिन्न गुणों के बीच सहसंबंध कैसे खोजें
* कुछ परिकल्पनाओं को साबित करने के लिए गणित और सांख्यिकी के सटीक उपकरणों का उपयोग कैसे करें
* दिए गए डेटा नमूने के लिए यादृच्छिक चर के विश्वास अंतराल की गणना कैसे करें
हालांकि यह संभावना और सांख्यिकी के भीतर मौजूद विषयों की पूरी सूची नहीं है, यह इस पाठ्यक्रम में एक अच्छी शुरुआत देने के लिए पर्याप्त होना चाहिए।
## 🚀 चुनौती
नोटबुक में दिए गए नमूना कोड का उपयोग करके अन्य परिकल्पनाओं का परीक्षण करें:
1. फर्स्ट बेसमैन सेकंड बेसमैन से बड़े हैं।
2. फर्स्ट बेसमैन थर्ड बेसमैन से ऊंचे हैं।
3. शॉर्टस्टॉप सेकंड बेसमैन से ऊंचे हैं।
## [पाठ के बाद क्विज़](https://ff-quizzes.netlify.app/en/ds/quiz/7)
## समीक्षा और स्व-अध्ययन
संभाव्यता और सांख्यिकी इतना व्यापक विषय है कि यह अपने स्वयं के पाठ्यक्रम के योग्य है। यदि आप सिद्धांत में गहराई तक जाना चाहते हैं, तो आप निम्नलिखित पुस्तकों को पढ़ना जारी रख सकते हैं:
1. [कार्लोस फर्नांडीज-ग्रांडा](https://cims.nyu.edu/~cfgranda/) न्यूयॉर्क विश्वविद्यालय से, जिनके पास [डेटा साइंस के लिए संभावना और सांख्यिकी](https://cims.nyu.edu/~cfgranda/pages/stuff/probability_stats_for_DS.pdf) पर शानदार व्याख्यान नोट्स हैं (ऑनलाइन उपलब्ध)।
2. [पीटर और एंड्रयू ब्रूस। डेटा वैज्ञानिकों के लिए व्यावहारिक सांख्यिकी।](https://www.oreilly.com/library/view/practical-statistics-for/9781491952955/) [[R में नमूना कोड](https://github.com/andrewgbruce/statistics-for-data-scientists)]।
3. [जेम्स डी. मिलर। डेटा साइंस के लिए सांख्यिकी](https://www.packtpub.com/product/statistics-for-data-science/9781788290678) [[R में नमूना कोड](https://github.com/PacktPublishing/Statistics-for-Data-Science)]।
## असाइनमेंट
[छोटा डायबिटीज़ अध्ययन](assignment.md)
## क्रेडिट्स
यह पाठ [दिमित्री सॉश्निकोव](http://soshnikov.com) द्वारा ♥️ के साथ लिखा गया है।
---
**अस्वीकरण**:
यह दस्तावेज़ AI अनुवाद सेवा [Co-op Translator](https://github.com/Azure/co-op-translator) का उपयोग करके अनुवादित किया गया है। जबकि हम सटीकता के लिए प्रयास करते हैं, कृपया ध्यान दें कि स्वचालित अनुवाद में त्रुटियां या अशुद्धियां हो सकती हैं। मूल भाषा में उपलब्ध मूल दस्तावेज़ को आधिकारिक स्रोत माना जाना चाहिए। महत्वपूर्ण जानकारी के लिए, पेशेवर मानव अनुवाद की सिफारिश की जाती है। इस अनुवाद के उपयोग से उत्पन्न किसी भी गलतफहमी या गलत व्याख्या के लिए हम उत्तरदायी नहीं हैं।
यहां हम **इंटर-क्वारटाइल रेंज** IQR=Q3-Q1 और तथाकथित **आउटलायर्स** - मान जो [Q1-1.5*IQR,Q3+1.5*IQR] की सीमाओं के बाहर होते हैं, की भी गणना करते हैं।
एक सीमित वितरण जिसमें संभावित मानों की संख्या कम होती है, एक अच्छा "विशिष्ट" मान वह होता है जो सबसे अधिक बार प्रकट होता है, जिसे **मोड** कहा जाता है। इसे अक्सर श्रेणीबद्ध डेटा, जैसे रंगों, पर लागू किया जाता है। मान लें कि हमारे पास दो समूह हैं - कुछ जो लाल रंग को पसंद करते हैं और अन्य जो नीले रंग को पसंद करते हैं। यदि हम रंगों को संख्याओं द्वारा कोड करते हैं, तो पसंदीदा रंग के लिए माध्य मान कहीं नारंगी-हरे स्पेक्ट्रम में होगा, जो किसी भी समूह की वास्तविक प्राथमिकता को इंगित नहीं करता। हालांकि, मोड या तो एक रंग होगा, या दोनों रंग होंगे, यदि उनके लिए मतदान करने वाले लोगों की संख्या समान है (इस मामले में हम नमूने को **मल्टीमोडल** कहते हैं)।
## वास्तविक दुनिया का डेटा
जब हम वास्तविक जीवन के डेटा का विश्लेषण करते हैं, तो वे अक्सर रैंडम वेरिएबल्स के रूप में नहीं होते हैं, इस अर्थ में कि हम अज्ञात परिणामों के साथ प्रयोग नहीं करते। उदाहरण के लिए, बेसबॉल खिलाड़ियों की एक टीम पर विचार करें, और उनके शरीर के डेटा, जैसे ऊंचाई, वजन और उम्र। ये संख्याएं बिल्कुल रैंडम नहीं हैं, लेकिन हम अभी भी उन्हीं गणितीय अवधारणाओं को लागू कर सकते हैं। उदाहरण के लिए, लोगों के वजन का अनुक्रम कुछ रैंडम वेरिएबल से लिए गए मानों का अनुक्रम माना जा सकता है। नीचे [मेजर लीग बेसबॉल](http://mlb.mlb.com/index.jsp) के वास्तविक बेसबॉल खिलाड़ियों के वजन का अनुक्रम दिया गया है, जो [इस डेटासेट](http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_MLB_HeightsWeights) से लिया गया है (आपकी सुविधा के लिए केवल पहले 20 मान दिखाए गए हैं):
```
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
```
> **नोट**: इस डेटासेट के साथ काम करने के उदाहरण को देखने के लिए, [संबंधित नोटबुक](notebook.ipynb) देखें। इस पाठ में कई चुनौतियां भी हैं, और आप उस नोटबुक में कुछ कोड जोड़कर उन्हें पूरा कर सकते हैं। यदि आप डेटा पर काम करने के तरीके के बारे में सुनिश्चित नहीं हैं, तो चिंता न करें - हम बाद में Python का उपयोग करके डेटा पर काम करने पर वापस आएंगे। यदि आप Jupyter Notebook में कोड चलाने का तरीका नहीं जानते हैं, तो [इस लेख](https://soshnikov.com/education/how-to-execute-notebooks-from-github/) को देखें।
यहां हमारे डेटा के लिए माध्य, माध्यिका और क्वारटाइल्स दिखाने वाला बॉक्स प्लॉट है:

चूंकि हमारे डेटा में विभिन्न खिलाड़ी **भूमिकाओं** की जानकारी है, हम भूमिका के अनुसार भी बॉक्स प्लॉट बना सकते हैं - यह हमें यह विचार करने की अनुमति देगा कि भूमिकाओं के बीच पैरामीटर मान कैसे भिन्न होते हैं। इस बार हम ऊंचाई पर विचार करेंगे:

यह आरेख सुझाव देता है कि, औसतन, पहले बेसमैन की ऊंचाई दूसरे बेसमैन की ऊंचाई से अधिक है। इस पाठ में बाद में हम सीखेंगे कि इस परिकल्पना को अधिक औपचारिक रूप से कैसे परीक्षण किया जा सकता है, और यह प्रदर्शित करने के लिए कि हमारे डेटा सांख्यिकीय रूप से महत्वपूर्ण है।
> जब वास्तविक दुनिया के डेटा के साथ काम करते हैं, तो हम मानते हैं कि सभी डेटा पॉइंट्स कुछ संभाव्यता वितरण से लिए गए नमूने हैं। यह धारणा हमें मशीन लर्निंग तकनीकों को लागू करने और काम करने वाले भविष्यवाणी मॉडल बनाने की अनुमति देती है।
हमारे डेटा का वितरण कैसा है, यह देखने के लिए हम **हिस्टोग्राम** नामक एक ग्राफ़ बना सकते हैं। X-अक्ष में विभिन्न वजन अंतराल (जिसे **बिन्स** कहा जाता है) की संख्या होगी, और वर्टिकल अक्ष दिखाएगा कि हमारा रैंडम वेरिएबल नमूना दिए गए अंतराल में कितनी बार था।

इस हिस्टोग्राम से आप देख सकते हैं कि सभी मान एक निश्चित माध्य वजन के आसपास केंद्रित हैं, और जैसे-जैसे हम उस वजन से दूर जाते हैं - उस मान के वजन कम बार मिलते हैं। यानी, यह बहुत ही असंभावित है कि बेसबॉल खिलाड़ी का वजन माध्य वजन से बहुत अलग होगा। वजन का विचरण दिखाता है कि वजन माध्य से कितना भिन्न होने की संभावना है।
> यदि हम अन्य लोगों के वजन लेते हैं, जो बेसबॉल लीग से नहीं हैं, तो वितरण अलग होने की संभावना है। हालांकि, वितरण का आकार समान रहेगा, लेकिन माध्य और विचरण बदल जाएंगे। इसलिए, यदि हम अपने मॉडल को बेसबॉल खिलाड़ियों पर प्रशिक्षित करते हैं, तो यह विश्वविद्यालय के छात्रों पर लागू होने पर गलत परिणाम देने की संभावना है, क्योंकि अंतर्निहित वितरण अलग है।
## नॉर्मल वितरण
ऊपर हमने जो वजन का वितरण देखा वह बहुत सामान्य है, और वास्तविक दुनिया से कई माप एक ही प्रकार के वितरण का पालन करते हैं, लेकिन अलग-अलग माध्य और विचरण के साथ। इस वितरण को **नॉर्मल वितरण** कहा जाता है, और यह सांख्यिकी में बहुत महत्वपूर्ण भूमिका निभाता है।
नॉर्मल वितरण का उपयोग संभावित बेसबॉल खिलाड़ियों के रैंडम वजन उत्पन्न करने का सही तरीका है। एक बार जब हम माध्य वजन `mean` और मानक विचलन `std` जानते हैं, तो हम निम्नलिखित तरीके से 1000 वजन नमूने उत्पन्न कर सकते हैं:
```python
samples = np.random.normal(mean,std,1000)
```
यदि हम उत्पन्न नमूनों का हिस्टोग्राम बनाते हैं, तो हम ऊपर दिखाए गए चित्र के समान चित्र देखेंगे। और यदि हम नमूनों की संख्या और बिन्स की संख्या बढ़ाते हैं, तो हम नॉर्मल वितरण की एक अधिक आदर्श तस्वीर उत्पन्न कर सकते हैं:

*माध्य=0 और मानक विचलन=1 के साथ नॉर्मल वितरण*
## विश्वास अंतराल
जब हम बेसबॉल खिलाड़ियों के वजन के बारे में बात करते हैं, तो हम मानते हैं कि एक निश्चित **रैंडम वेरिएबल W** है जो सभी बेसबॉल खिलाड़ियों के वजन के आदर्श संभाव्यता वितरण (जिसे **जनसंख्या** कहा जाता है) से मेल खाता है। हमारे वजन का अनुक्रम सभी बेसबॉल खिलाड़ियों के एक उपसमुच्चय से मेल खाता है जिसे हम **नमूना** कहते हैं। एक दिलचस्प सवाल यह है कि क्या हम W के वितरण के पैरामीटर, यानी जनसंख्या के माध्य और विचरण को जान सकते हैं?
सबसे आसान उत्तर होगा हमारे नमूने के माध्य और विचरण की गणना करना। हालांकि, ऐसा हो सकता है कि हमारा रैंडम नमूना पूरी जनसंख्या का सटीक प्रतिनिधित्व न करे। इसलिए **विश्वास अंतराल** के बारे में बात करना समझ में आता है।
> **विश्वास अंतराल** हमारे नमूने को देखते हुए जनसंख्या के वास्तविक माध्य का अनुमान है, जो एक निश्चित संभावना (या **विश्वास स्तर**) में सटीक है।
मान लें कि हमारे पास एक नमूना X
1, ..., Xn को हमारे वितरण से चुना गया है। हर बार जब हम अपने वितरण से एक नमूना लेते हैं, तो हमें अलग-अलग औसत मान μ प्राप्त होगा। इसलिए μ को एक यादृच्छिक चर माना जा सकता है। एक **विश्वास अंतराल** (confidence interval) जिसमें विश्वास p है, वह दो मानों (Lp,Rp) का एक युग्म है, ऐसा कि **P**(Lp≤μ≤Rp) = p, यानी मापा गया औसत मान इस अंतराल में आने की संभावना p के बराबर है।
यह हमारी छोटी सी भूमिका से परे है कि हम विस्तार से चर्चा करें कि इन विश्वास अंतरालों की गणना कैसे की जाती है। कुछ और विवरण [विकिपीडिया](https://en.wikipedia.org/wiki/Confidence_interval) पर पाए जा सकते हैं। संक्षेप में, हम वास्तविक जनसंख्या औसत के सापेक्ष गणना किए गए नमूना औसत के वितरण को परिभाषित करते हैं, जिसे **स्टूडेंट वितरण** (student distribution) कहा जाता है।
> **रोचक तथ्य**: स्टूडेंट वितरण का नाम गणितज्ञ विलियम सीली गॉसेट के नाम पर रखा गया है, जिन्होंने "स्टूडेंट" उपनाम के तहत अपना पेपर प्रकाशित किया। वे गिनीज ब्रुअरी में काम करते थे, और एक संस्करण के अनुसार, उनके नियोक्ता नहीं चाहते थे कि आम जनता को पता चले कि वे कच्चे माल की गुणवत्ता निर्धारित करने के लिए सांख्यिकीय परीक्षणों का उपयोग कर रहे थे।
यदि हम अपनी जनसंख्या के औसत μ का p विश्वास के साथ अनुमान लगाना चाहते हैं, तो हमें स्टूडेंट वितरण A का *(1-p)/2-थ परसेंटाइल* लेना होगा, जिसे या तो तालिकाओं से लिया जा सकता है, या सांख्यिकीय सॉफ़्टवेयर (जैसे Python, R, आदि) के कुछ अंतर्निर्मित कार्यों का उपयोग करके कंप्यूटर पर गणना की जा सकती है। फिर μ के लिए अंतराल X±A*D/√n होगा, जहां X नमूने का प्राप्त औसत है, और D मानक विचलन है।
> **ध्यान दें**: हम [स्वतंत्रता की डिग्री](https://en.wikipedia.org/wiki/Degrees_of_freedom_(statistics)) की एक महत्वपूर्ण अवधारणा की चर्चा को भी छोड़ देते हैं, जो स्टूडेंट वितरण के संदर्भ में महत्वपूर्ण है। इस अवधारणा को गहराई से समझने के लिए आप सांख्यिकी पर अधिक पूर्ण पुस्तकों का संदर्भ ले सकते हैं।
वज़न और ऊंचाई के लिए विश्वास अंतराल की गणना का एक उदाहरण [संबंधित नोटबुक](notebook.ipynb) में दिया गया है।
| p | वज़न औसत |
|-----|-----------|
| 0.85 | 201.73±0.94 |
| 0.90 | 201.73±1.08 |
| 0.95 | 201.73±1.28 |
ध्यान दें कि विश्वास संभावना जितनी अधिक होती है, विश्वास अंतराल उतना ही चौड़ा होता है।
## परिकल्पना परीक्षण
हमारे बेसबॉल खिलाड़ियों के डेटासेट में, विभिन्न खिलाड़ी भूमिकाएँ हैं, जिन्हें नीचे सारांशित किया जा सकता है (कैसे यह तालिका गणना की गई है, यह देखने के लिए [संबंधित नोटबुक](notebook.ipynb) देखें):
| भूमिका | ऊंचाई | वज़न | संख्या |
|------|--------|--------|-------|
| कैचर | 72.723684 | 204.328947 | 76 |
| डिज़िग्नेटेड हिटर | 74.222222 | 220.888889 | 18 |
| फर्स्ट बेसमैन | 74.000000 | 213.109091 | 55 |
| आउटफील्डर | 73.010309 | 199.113402 | 194 |
| रिलीफ पिचर | 74.374603 | 203.517460 | 315 |
| सेकंड बेसमैन | 71.362069 | 184.344828 | 58 |
| शॉर्टस्टॉप | 71.903846 | 182.923077 | 52 |
| स्टार्टिंग पिचर | 74.719457 | 205.163636 | 221 |
| थर्ड बेसमैन | 73.044444 | 200.955556 | 45 |
हम देख सकते हैं कि फर्स्ट बेसमैन की औसत ऊंचाई सेकंड बेसमैन से अधिक है। इसलिए, हम यह निष्कर्ष निकालने के लिए प्रेरित हो सकते हैं कि **फर्स्ट बेसमैन सेकंड बेसमैन से ऊंचे होते हैं**।
> इस कथन को **एक परिकल्पना** कहा जाता है, क्योंकि हमें नहीं पता कि यह तथ्य वास्तव में सत्य है या नहीं।
हालांकि, यह हमेशा स्पष्ट नहीं होता कि हम यह निष्कर्ष निकाल सकते हैं या नहीं। ऊपर की चर्चा से हमें पता है कि प्रत्येक औसत का एक संबंधित विश्वास अंतराल होता है, और इसलिए यह अंतर केवल एक सांख्यिकीय त्रुटि हो सकता है। हमें अपनी परिकल्पना का परीक्षण करने के लिए कुछ अधिक औपचारिक तरीके की आवश्यकता है।
आइए फर्स्ट और सेकंड बेसमैन की ऊंचाई के लिए विश्वास अंतराल को अलग-अलग गणना करें:
| विश्वास | फर्स्ट बेसमैन | सेकंड बेसमैन |
|------------|---------------|----------------|
| 0.85 | 73.62..74.38 | 71.04..71.69 |
| 0.90 | 73.56..74.44 | 70.99..71.73 |
| 0.95 | 73.47..74.53 | 70.92..71.81 |
हम देख सकते हैं कि किसी भी विश्वास स्तर पर अंतराल ओवरलैप नहीं करते। यह हमारी परिकल्पना को साबित करता है कि फर्स्ट बेसमैन सेकंड बेसमैन से ऊंचे होते हैं।
औपचारिक रूप से, हम जो समस्या हल कर रहे हैं वह यह देखना है कि **दो संभाव्यता वितरण समान हैं या नहीं**, या कम से कम उनके मापदंड समान हैं। वितरण के आधार पर, हमें इसके लिए अलग-अलग परीक्षणों का उपयोग करना होगा। यदि हमें पता है कि हमारे वितरण सामान्य हैं, तो हम **[स्टूडेंट t-परीक्षण](https://en.wikipedia.org/wiki/Student%27s_t-test)** लागू कर सकते हैं।
स्टूडेंट t-परीक्षण में, हम तथाकथित **t-मूल्य** की गणना करते हैं, जो औसतों के बीच के अंतर को, विचलन को ध्यान में रखते हुए, इंगित करता है। यह प्रदर्शित किया गया है कि t-मूल्य **स्टूडेंट वितरण** का अनुसरण करता है, जो हमें दिए गए विश्वास स्तर **p** के लिए सीमा मान प्राप्त करने की अनुमति देता है (यह गणना की जा सकती है, या संख्यात्मक तालिकाओं में देखा जा सकता है)। फिर हम t-मूल्य की तुलना इस सीमा से करते हैं ताकि परिकल्पना को स्वीकार या अस्वीकार कर सकें।
Python में, हम **SciPy** पैकेज का उपयोग कर सकते हैं, जिसमें `ttest_ind` फ़ंक्शन शामिल है (साथ ही कई अन्य उपयोगी सांख्यिकीय फ़ंक्शन!)। यह हमारे लिए t-मूल्य की गणना करता है, और विश्वास p-मूल्य का रिवर्स लुकअप भी करता है, ताकि हम केवल विश्वास को देखकर निष्कर्ष निकाल सकें।
उदाहरण के लिए, फर्स्ट और सेकंड बेसमैन की ऊंचाई की तुलना हमें निम्नलिखित परिणाम देती है:
```python
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
```
```
T-value = 7.65
P-value: 9.137321189738925e-12
```
हमारे मामले में, p-मूल्य बहुत कम है, जिसका अर्थ है कि फर्स्ट बेसमैन के ऊंचे होने का मजबूत प्रमाण है।
इसके अलावा, अन्य प्रकार की परिकल्पनाएँ भी हो सकती हैं जिन्हें हम परीक्षण करना चाह सकते हैं, जैसे:
* यह साबित करना कि कोई दिया गया नमूना किसी वितरण का अनुसरण करता है। हमारे मामले में हमने मान लिया है कि ऊंचाई सामान्य रूप से वितरित है, लेकिन इसे औपचारिक सांख्यिकीय सत्यापन की आवश्यकता है।
* यह साबित करना कि किसी नमूने का औसत मान किसी पूर्वनिर्धारित मान से मेल खाता है।
* कई नमूनों के औसतों की तुलना करना (जैसे, विभिन्न आयु समूहों में खुशी के स्तर में क्या अंतर है)।
## बड़े संख्याओं का नियम और केंद्रीय सीमा प्रमेय
सामान्य वितरण इतना महत्वपूर्ण क्यों है, इसका एक कारण **केंद्रीय सीमा प्रमेय** (central limit theorem) है। मान लें कि हमारे पास स्वतंत्र N मानों X1, ..., XN का एक बड़ा नमूना है, जिसे किसी भी वितरण से लिया गया है, जिसका औसत μ और विचरण σ2 है। फिर, पर्याप्त बड़े N के लिए (दूसरे शब्दों में, जब N→∞), ΣiXi का औसत सामान्य रूप से वितरित होगा, जिसका औसत μ और विचरण σ2/N होगा।
> केंद्रीय सीमा प्रमेय की एक और व्याख्या यह है कि यह कहता है कि किसी भी यादृच्छिक चर मानों के योग का औसत निकालने पर आप सामान्य वितरण प्राप्त करते हैं।
केंद्रीय सीमा प्रमेय से यह भी पता चलता है कि, जब N→∞, नमूना औसत के μ के बराबर होने की संभावना 1 हो जाती है। इसे **बड़े संख्याओं का नियम** (law of large numbers) कहा जाता है।
## सहसंबंध और सहभिन्नता
डेटा साइंस का एक काम डेटा के बीच संबंध खोजना है। हम कहते हैं कि दो अनुक्रम **सहसंबद्ध** (correlate) हैं जब वे एक ही समय में समान व्यवहार प्रदर्शित करते हैं, यानी वे या तो एक साथ बढ़ते/घटते हैं, या एक अनुक्रम बढ़ता है जब दूसरा घटता है और इसके विपरीत। दूसरे शब्दों में, ऐसा लगता है कि दो अनुक्रमों के बीच कुछ संबंध है।
> सहसंबंध जरूरी नहीं कि दो अनुक्रमों के बीच कारणात्मक संबंध को इंगित करता है; कभी-कभी दोनों चर किसी बाहरी कारण पर निर्भर हो सकते हैं, या यह केवल संयोग से हो सकता है कि दोनों अनुक्रम सहसंबद्ध हैं। हालांकि, मजबूत गणितीय सहसंबंध इस बात का अच्छा संकेत है कि दो चर किसी न किसी तरह से जुड़े हुए हैं।
गणितीय रूप से, दो यादृच्छिक चरों के बीच संबंध दिखाने वाली मुख्य अवधारणा **सहभिन्नता** (covariance) है, जिसे इस प्रकार गणना किया जाता है: Cov(X,Y) = **E**\[(X-**E**(X))(Y-**E**(Y))\]। हम दोनों चरों के उनके औसत मानों से विचलन की गणना करते हैं, और फिर उन विचलनों के गुणनफल को लेते हैं। यदि दोनों चर एक साथ विचलित होते हैं, तो गुणनफल हमेशा एक सकारात्मक मान होगा, जो सकारात्मक सहभिन्नता में जुड़ जाएगा। यदि दोनों चर असंगत रूप से विचलित होते हैं (यानी एक औसत से नीचे गिरता है जब दूसरा औसत से ऊपर उठता है), तो हमें हमेशा नकारात्मक संख्याएँ मिलेंगी, जो नकारात्मक सहभिन्नता में जुड़ेंगी। यदि विचलन स्वतंत्र हैं, तो वे लगभग शून्य में जुड़ेंगे।
सहभिन्नता का परिमाण हमें यह नहीं बताता कि सहसंबंध कितना बड़ा है, क्योंकि यह वास्तविक मानों के परिमाण पर निर्भर करता है। इसे सामान्यीकृत करने के लिए, हम सहभिन्नता को दोनों चरों के मानक विचलन से विभाजित कर सकते हैं, ताकि **सहसंबंध** प्राप्त हो। अच्छी बात यह है कि सहसंबंध हमेशा [-1,1] की सीमा में होता है, जहां 1 मानों के बीच मजबूत सकारात्मक सहसंबंध को इंगित करता है, -1 - मजबूत नकारात्मक सहसंबंध, और 0 - बिल्कुल भी सहसंबंध नहीं (चर स्वतंत्र हैं)।
**उदाहरण**: हम ऊपर उल्लिखित बेसबॉल खिलाड़ियों के डेटासेट से वज़न और ऊंचाई के बीच सहसंबंध की गणना कर सकते हैं:
```python
print(np.corrcoef(weights,heights))
```
परिणामस्वरूप, हमें इस प्रकार का **सहसंबंध मैट्रिक्स** मिलता है:
```
array([[1. , 0.52959196],
[0.52959196, 1. ]])
```
> सहसंबंध मैट्रिक्स C किसी भी संख्या के इनपुट अनुक्रमों S1, ..., Sn के लिए गणना की जा सकती है। Cij का मान Si और Sj के बीच सहसंबंध है, और विकर्ण तत्व हमेशा 1 होते हैं (जो Si का आत्म-सहसंबंध भी है)।
हमारे मामले में, मान 0.53 इंगित करता है कि किसी व्यक्ति के वज़न और ऊंचाई के बीच कुछ सहसंबंध है। हम एक मान को दूसरे के खिलाफ बिखराव प्लॉट भी बना सकते हैं ताकि संबंध को दृश्य रूप से देखा जा सके:

> सहसंबंध और सहभिन्नता के और उदाहरण [संबंधित नोटबुक](notebook.ipynb) में पाए जा सकते हैं।
## निष्कर्ष
इस खंड में, हमने सीखा:
* डेटा के बुनियादी सांख्यिकीय गुण, जैसे औसत, विचरण, माध्यिका और चतुर्थांश
* यादृच्छिक चरों के विभिन्न वितरण, जिसमें सामान्य वितरण शामिल है
* विभिन्न गुणों के बीच सहसंबंध कैसे खोजें
* कुछ परिकल्पनाओं को साबित करने के लिए गणित और सांख्यिकी के सटीक उपकरणों का उपयोग कैसे करें
* दिए गए डेटा नमूने के लिए यादृच्छिक चर के विश्वास अंतराल की गणना कैसे करें
हालांकि यह संभावना और सांख्यिकी के भीतर मौजूद विषयों की पूरी सूची नहीं है, यह इस पाठ्यक्रम में एक अच्छी शुरुआत देने के लिए पर्याप्त होना चाहिए।
## 🚀 चुनौती
नोटबुक में दिए गए नमूना कोड का उपयोग करके अन्य परिकल्पनाओं का परीक्षण करें:
1. फर्स्ट बेसमैन सेकंड बेसमैन से बड़े हैं।
2. फर्स्ट बेसमैन थर्ड बेसमैन से ऊंचे हैं।
3. शॉर्टस्टॉप सेकंड बेसमैन से ऊंचे हैं।
## [पाठ के बाद क्विज़](https://ff-quizzes.netlify.app/en/ds/quiz/7)
## समीक्षा और स्व-अध्ययन
संभाव्यता और सांख्यिकी इतना व्यापक विषय है कि यह अपने स्वयं के पाठ्यक्रम के योग्य है। यदि आप सिद्धांत में गहराई तक जाना चाहते हैं, तो आप निम्नलिखित पुस्तकों को पढ़ना जारी रख सकते हैं:
1. [कार्लोस फर्नांडीज-ग्रांडा](https://cims.nyu.edu/~cfgranda/) न्यूयॉर्क विश्वविद्यालय से, जिनके पास [डेटा साइंस के लिए संभावना और सांख्यिकी](https://cims.nyu.edu/~cfgranda/pages/stuff/probability_stats_for_DS.pdf) पर शानदार व्याख्यान नोट्स हैं (ऑनलाइन उपलब्ध)।
2. [पीटर और एंड्रयू ब्रूस। डेटा वैज्ञानिकों के लिए व्यावहारिक सांख्यिकी।](https://www.oreilly.com/library/view/practical-statistics-for/9781491952955/) [[R में नमूना कोड](https://github.com/andrewgbruce/statistics-for-data-scientists)]।
3. [जेम्स डी. मिलर। डेटा साइंस के लिए सांख्यिकी](https://www.packtpub.com/product/statistics-for-data-science/9781788290678) [[R में नमूना कोड](https://github.com/PacktPublishing/Statistics-for-Data-Science)]।
## असाइनमेंट
[छोटा डायबिटीज़ अध्ययन](assignment.md)
## क्रेडिट्स
यह पाठ [दिमित्री सॉश्निकोव](http://soshnikov.com) द्वारा ♥️ के साथ लिखा गया है।
---
**अस्वीकरण**:
यह दस्तावेज़ AI अनुवाद सेवा [Co-op Translator](https://github.com/Azure/co-op-translator) का उपयोग करके अनुवादित किया गया है। जबकि हम सटीकता के लिए प्रयास करते हैं, कृपया ध्यान दें कि स्वचालित अनुवाद में त्रुटियां या अशुद्धियां हो सकती हैं। मूल भाषा में उपलब्ध मूल दस्तावेज़ को आधिकारिक स्रोत माना जाना चाहिए। महत्वपूर्ण जानकारी के लिए, पेशेवर मानव अनुवाद की सिफारिश की जाती है। इस अनुवाद के उपयोग से उत्पन्न किसी भी गलतफहमी या गलत व्याख्या के लिए हम उत्तरदायी नहीं हैं।  यहां हम **इंटर-क्वारटाइल रेंज** IQR=Q3-Q1 और तथाकथित **आउटलायर्स** - मान जो [Q1-1.5*IQR,Q3+1.5*IQR] की सीमाओं के बाहर होते हैं, की भी गणना करते हैं।
एक सीमित वितरण जिसमें संभावित मानों की संख्या कम होती है, एक अच्छा "विशिष्ट" मान वह होता है जो सबसे अधिक बार प्रकट होता है, जिसे **मोड** कहा जाता है। इसे अक्सर श्रेणीबद्ध डेटा, जैसे रंगों, पर लागू किया जाता है। मान लें कि हमारे पास दो समूह हैं - कुछ जो लाल रंग को पसंद करते हैं और अन्य जो नीले रंग को पसंद करते हैं। यदि हम रंगों को संख्याओं द्वारा कोड करते हैं, तो पसंदीदा रंग के लिए माध्य मान कहीं नारंगी-हरे स्पेक्ट्रम में होगा, जो किसी भी समूह की वास्तविक प्राथमिकता को इंगित नहीं करता। हालांकि, मोड या तो एक रंग होगा, या दोनों रंग होंगे, यदि उनके लिए मतदान करने वाले लोगों की संख्या समान है (इस मामले में हम नमूने को **मल्टीमोडल** कहते हैं)।
## वास्तविक दुनिया का डेटा
जब हम वास्तविक जीवन के डेटा का विश्लेषण करते हैं, तो वे अक्सर रैंडम वेरिएबल्स के रूप में नहीं होते हैं, इस अर्थ में कि हम अज्ञात परिणामों के साथ प्रयोग नहीं करते। उदाहरण के लिए, बेसबॉल खिलाड़ियों की एक टीम पर विचार करें, और उनके शरीर के डेटा, जैसे ऊंचाई, वजन और उम्र। ये संख्याएं बिल्कुल रैंडम नहीं हैं, लेकिन हम अभी भी उन्हीं गणितीय अवधारणाओं को लागू कर सकते हैं। उदाहरण के लिए, लोगों के वजन का अनुक्रम कुछ रैंडम वेरिएबल से लिए गए मानों का अनुक्रम माना जा सकता है। नीचे [मेजर लीग बेसबॉल](http://mlb.mlb.com/index.jsp) के वास्तविक बेसबॉल खिलाड़ियों के वजन का अनुक्रम दिया गया है, जो [इस डेटासेट](http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_MLB_HeightsWeights) से लिया गया है (आपकी सुविधा के लिए केवल पहले 20 मान दिखाए गए हैं):
```
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
```
> **नोट**: इस डेटासेट के साथ काम करने के उदाहरण को देखने के लिए, [संबंधित नोटबुक](notebook.ipynb) देखें। इस पाठ में कई चुनौतियां भी हैं, और आप उस नोटबुक में कुछ कोड जोड़कर उन्हें पूरा कर सकते हैं। यदि आप डेटा पर काम करने के तरीके के बारे में सुनिश्चित नहीं हैं, तो चिंता न करें - हम बाद में Python का उपयोग करके डेटा पर काम करने पर वापस आएंगे। यदि आप Jupyter Notebook में कोड चलाने का तरीका नहीं जानते हैं, तो [इस लेख](https://soshnikov.com/education/how-to-execute-notebooks-from-github/) को देखें।
यहां हमारे डेटा के लिए माध्य, माध्यिका और क्वारटाइल्स दिखाने वाला बॉक्स प्लॉट है:

चूंकि हमारे डेटा में विभिन्न खिलाड़ी **भूमिकाओं** की जानकारी है, हम भूमिका के अनुसार भी बॉक्स प्लॉट बना सकते हैं - यह हमें यह विचार करने की अनुमति देगा कि भूमिकाओं के बीच पैरामीटर मान कैसे भिन्न होते हैं। इस बार हम ऊंचाई पर विचार करेंगे:

यह आरेख सुझाव देता है कि, औसतन, पहले बेसमैन की ऊंचाई दूसरे बेसमैन की ऊंचाई से अधिक है। इस पाठ में बाद में हम सीखेंगे कि इस परिकल्पना को अधिक औपचारिक रूप से कैसे परीक्षण किया जा सकता है, और यह प्रदर्शित करने के लिए कि हमारे डेटा सांख्यिकीय रूप से महत्वपूर्ण है।
> जब वास्तविक दुनिया के डेटा के साथ काम करते हैं, तो हम मानते हैं कि सभी डेटा पॉइंट्स कुछ संभाव्यता वितरण से लिए गए नमूने हैं। यह धारणा हमें मशीन लर्निंग तकनीकों को लागू करने और काम करने वाले भविष्यवाणी मॉडल बनाने की अनुमति देती है।
हमारे डेटा का वितरण कैसा है, यह देखने के लिए हम **हिस्टोग्राम** नामक एक ग्राफ़ बना सकते हैं। X-अक्ष में विभिन्न वजन अंतराल (जिसे **बिन्स** कहा जाता है) की संख्या होगी, और वर्टिकल अक्ष दिखाएगा कि हमारा रैंडम वेरिएबल नमूना दिए गए अंतराल में कितनी बार था।

इस हिस्टोग्राम से आप देख सकते हैं कि सभी मान एक निश्चित माध्य वजन के आसपास केंद्रित हैं, और जैसे-जैसे हम उस वजन से दूर जाते हैं - उस मान के वजन कम बार मिलते हैं। यानी, यह बहुत ही असंभावित है कि बेसबॉल खिलाड़ी का वजन माध्य वजन से बहुत अलग होगा। वजन का विचरण दिखाता है कि वजन माध्य से कितना भिन्न होने की संभावना है।
> यदि हम अन्य लोगों के वजन लेते हैं, जो बेसबॉल लीग से नहीं हैं, तो वितरण अलग होने की संभावना है। हालांकि, वितरण का आकार समान रहेगा, लेकिन माध्य और विचरण बदल जाएंगे। इसलिए, यदि हम अपने मॉडल को बेसबॉल खिलाड़ियों पर प्रशिक्षित करते हैं, तो यह विश्वविद्यालय के छात्रों पर लागू होने पर गलत परिणाम देने की संभावना है, क्योंकि अंतर्निहित वितरण अलग है।
## नॉर्मल वितरण
ऊपर हमने जो वजन का वितरण देखा वह बहुत सामान्य है, और वास्तविक दुनिया से कई माप एक ही प्रकार के वितरण का पालन करते हैं, लेकिन अलग-अलग माध्य और विचरण के साथ। इस वितरण को **नॉर्मल वितरण** कहा जाता है, और यह सांख्यिकी में बहुत महत्वपूर्ण भूमिका निभाता है।
नॉर्मल वितरण का उपयोग संभावित बेसबॉल खिलाड़ियों के रैंडम वजन उत्पन्न करने का सही तरीका है। एक बार जब हम माध्य वजन `mean` और मानक विचलन `std` जानते हैं, तो हम निम्नलिखित तरीके से 1000 वजन नमूने उत्पन्न कर सकते हैं:
```python
samples = np.random.normal(mean,std,1000)
```
यदि हम उत्पन्न नमूनों का हिस्टोग्राम बनाते हैं, तो हम ऊपर दिखाए गए चित्र के समान चित्र देखेंगे। और यदि हम नमूनों की संख्या और बिन्स की संख्या बढ़ाते हैं, तो हम नॉर्मल वितरण की एक अधिक आदर्श तस्वीर उत्पन्न कर सकते हैं:

*माध्य=0 और मानक विचलन=1 के साथ नॉर्मल वितरण*
## विश्वास अंतराल
जब हम बेसबॉल खिलाड़ियों के वजन के बारे में बात करते हैं, तो हम मानते हैं कि एक निश्चित **रैंडम वेरिएबल W** है जो सभी बेसबॉल खिलाड़ियों के वजन के आदर्श संभाव्यता वितरण (जिसे **जनसंख्या** कहा जाता है) से मेल खाता है। हमारे वजन का अनुक्रम सभी बेसबॉल खिलाड़ियों के एक उपसमुच्चय से मेल खाता है जिसे हम **नमूना** कहते हैं। एक दिलचस्प सवाल यह है कि क्या हम W के वितरण के पैरामीटर, यानी जनसंख्या के माध्य और विचरण को जान सकते हैं?
सबसे आसान उत्तर होगा हमारे नमूने के माध्य और विचरण की गणना करना। हालांकि, ऐसा हो सकता है कि हमारा रैंडम नमूना पूरी जनसंख्या का सटीक प्रतिनिधित्व न करे। इसलिए **विश्वास अंतराल** के बारे में बात करना समझ में आता है।
> **विश्वास अंतराल** हमारे नमूने को देखते हुए जनसंख्या के वास्तविक माध्य का अनुमान है, जो एक निश्चित संभावना (या **विश्वास स्तर**) में सटीक है।
मान लें कि हमारे पास एक नमूना X
1, ..., Xn को हमारे वितरण से चुना गया है। हर बार जब हम अपने वितरण से एक नमूना लेते हैं, तो हमें अलग-अलग औसत मान μ प्राप्त होगा। इसलिए μ को एक यादृच्छिक चर माना जा सकता है। एक **विश्वास अंतराल** (confidence interval) जिसमें विश्वास p है, वह दो मानों (Lp,Rp) का एक युग्म है, ऐसा कि **P**(Lp≤μ≤Rp) = p, यानी मापा गया औसत मान इस अंतराल में आने की संभावना p के बराबर है।
यह हमारी छोटी सी भूमिका से परे है कि हम विस्तार से चर्चा करें कि इन विश्वास अंतरालों की गणना कैसे की जाती है। कुछ और विवरण [विकिपीडिया](https://en.wikipedia.org/wiki/Confidence_interval) पर पाए जा सकते हैं। संक्षेप में, हम वास्तविक जनसंख्या औसत के सापेक्ष गणना किए गए नमूना औसत के वितरण को परिभाषित करते हैं, जिसे **स्टूडेंट वितरण** (student distribution) कहा जाता है।
> **रोचक तथ्य**: स्टूडेंट वितरण का नाम गणितज्ञ विलियम सीली गॉसेट के नाम पर रखा गया है, जिन्होंने "स्टूडेंट" उपनाम के तहत अपना पेपर प्रकाशित किया। वे गिनीज ब्रुअरी में काम करते थे, और एक संस्करण के अनुसार, उनके नियोक्ता नहीं चाहते थे कि आम जनता को पता चले कि वे कच्चे माल की गुणवत्ता निर्धारित करने के लिए सांख्यिकीय परीक्षणों का उपयोग कर रहे थे।
यदि हम अपनी जनसंख्या के औसत μ का p विश्वास के साथ अनुमान लगाना चाहते हैं, तो हमें स्टूडेंट वितरण A का *(1-p)/2-थ परसेंटाइल* लेना होगा, जिसे या तो तालिकाओं से लिया जा सकता है, या सांख्यिकीय सॉफ़्टवेयर (जैसे Python, R, आदि) के कुछ अंतर्निर्मित कार्यों का उपयोग करके कंप्यूटर पर गणना की जा सकती है। फिर μ के लिए अंतराल X±A*D/√n होगा, जहां X नमूने का प्राप्त औसत है, और D मानक विचलन है।
> **ध्यान दें**: हम [स्वतंत्रता की डिग्री](https://en.wikipedia.org/wiki/Degrees_of_freedom_(statistics)) की एक महत्वपूर्ण अवधारणा की चर्चा को भी छोड़ देते हैं, जो स्टूडेंट वितरण के संदर्भ में महत्वपूर्ण है। इस अवधारणा को गहराई से समझने के लिए आप सांख्यिकी पर अधिक पूर्ण पुस्तकों का संदर्भ ले सकते हैं।
वज़न और ऊंचाई के लिए विश्वास अंतराल की गणना का एक उदाहरण [संबंधित नोटबुक](notebook.ipynb) में दिया गया है।
| p | वज़न औसत |
|-----|-----------|
| 0.85 | 201.73±0.94 |
| 0.90 | 201.73±1.08 |
| 0.95 | 201.73±1.28 |
ध्यान दें कि विश्वास संभावना जितनी अधिक होती है, विश्वास अंतराल उतना ही चौड़ा होता है।
## परिकल्पना परीक्षण
हमारे बेसबॉल खिलाड़ियों के डेटासेट में, विभिन्न खिलाड़ी भूमिकाएँ हैं, जिन्हें नीचे सारांशित किया जा सकता है (कैसे यह तालिका गणना की गई है, यह देखने के लिए [संबंधित नोटबुक](notebook.ipynb) देखें):
| भूमिका | ऊंचाई | वज़न | संख्या |
|------|--------|--------|-------|
| कैचर | 72.723684 | 204.328947 | 76 |
| डिज़िग्नेटेड हिटर | 74.222222 | 220.888889 | 18 |
| फर्स्ट बेसमैन | 74.000000 | 213.109091 | 55 |
| आउटफील्डर | 73.010309 | 199.113402 | 194 |
| रिलीफ पिचर | 74.374603 | 203.517460 | 315 |
| सेकंड बेसमैन | 71.362069 | 184.344828 | 58 |
| शॉर्टस्टॉप | 71.903846 | 182.923077 | 52 |
| स्टार्टिंग पिचर | 74.719457 | 205.163636 | 221 |
| थर्ड बेसमैन | 73.044444 | 200.955556 | 45 |
हम देख सकते हैं कि फर्स्ट बेसमैन की औसत ऊंचाई सेकंड बेसमैन से अधिक है। इसलिए, हम यह निष्कर्ष निकालने के लिए प्रेरित हो सकते हैं कि **फर्स्ट बेसमैन सेकंड बेसमैन से ऊंचे होते हैं**।
> इस कथन को **एक परिकल्पना** कहा जाता है, क्योंकि हमें नहीं पता कि यह तथ्य वास्तव में सत्य है या नहीं।
हालांकि, यह हमेशा स्पष्ट नहीं होता कि हम यह निष्कर्ष निकाल सकते हैं या नहीं। ऊपर की चर्चा से हमें पता है कि प्रत्येक औसत का एक संबंधित विश्वास अंतराल होता है, और इसलिए यह अंतर केवल एक सांख्यिकीय त्रुटि हो सकता है। हमें अपनी परिकल्पना का परीक्षण करने के लिए कुछ अधिक औपचारिक तरीके की आवश्यकता है।
आइए फर्स्ट और सेकंड बेसमैन की ऊंचाई के लिए विश्वास अंतराल को अलग-अलग गणना करें:
| विश्वास | फर्स्ट बेसमैन | सेकंड बेसमैन |
|------------|---------------|----------------|
| 0.85 | 73.62..74.38 | 71.04..71.69 |
| 0.90 | 73.56..74.44 | 70.99..71.73 |
| 0.95 | 73.47..74.53 | 70.92..71.81 |
हम देख सकते हैं कि किसी भी विश्वास स्तर पर अंतराल ओवरलैप नहीं करते। यह हमारी परिकल्पना को साबित करता है कि फर्स्ट बेसमैन सेकंड बेसमैन से ऊंचे होते हैं।
औपचारिक रूप से, हम जो समस्या हल कर रहे हैं वह यह देखना है कि **दो संभाव्यता वितरण समान हैं या नहीं**, या कम से कम उनके मापदंड समान हैं। वितरण के आधार पर, हमें इसके लिए अलग-अलग परीक्षणों का उपयोग करना होगा। यदि हमें पता है कि हमारे वितरण सामान्य हैं, तो हम **[स्टूडेंट t-परीक्षण](https://en.wikipedia.org/wiki/Student%27s_t-test)** लागू कर सकते हैं।
स्टूडेंट t-परीक्षण में, हम तथाकथित **t-मूल्य** की गणना करते हैं, जो औसतों के बीच के अंतर को, विचलन को ध्यान में रखते हुए, इंगित करता है। यह प्रदर्शित किया गया है कि t-मूल्य **स्टूडेंट वितरण** का अनुसरण करता है, जो हमें दिए गए विश्वास स्तर **p** के लिए सीमा मान प्राप्त करने की अनुमति देता है (यह गणना की जा सकती है, या संख्यात्मक तालिकाओं में देखा जा सकता है)। फिर हम t-मूल्य की तुलना इस सीमा से करते हैं ताकि परिकल्पना को स्वीकार या अस्वीकार कर सकें।
Python में, हम **SciPy** पैकेज का उपयोग कर सकते हैं, जिसमें `ttest_ind` फ़ंक्शन शामिल है (साथ ही कई अन्य उपयोगी सांख्यिकीय फ़ंक्शन!)। यह हमारे लिए t-मूल्य की गणना करता है, और विश्वास p-मूल्य का रिवर्स लुकअप भी करता है, ताकि हम केवल विश्वास को देखकर निष्कर्ष निकाल सकें।
उदाहरण के लिए, फर्स्ट और सेकंड बेसमैन की ऊंचाई की तुलना हमें निम्नलिखित परिणाम देती है:
```python
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
```
```
T-value = 7.65
P-value: 9.137321189738925e-12
```
हमारे मामले में, p-मूल्य बहुत कम है, जिसका अर्थ है कि फर्स्ट बेसमैन के ऊंचे होने का मजबूत प्रमाण है।
इसके अलावा, अन्य प्रकार की परिकल्पनाएँ भी हो सकती हैं जिन्हें हम परीक्षण करना चाह सकते हैं, जैसे:
* यह साबित करना कि कोई दिया गया नमूना किसी वितरण का अनुसरण करता है। हमारे मामले में हमने मान लिया है कि ऊंचाई सामान्य रूप से वितरित है, लेकिन इसे औपचारिक सांख्यिकीय सत्यापन की आवश्यकता है।
* यह साबित करना कि किसी नमूने का औसत मान किसी पूर्वनिर्धारित मान से मेल खाता है।
* कई नमूनों के औसतों की तुलना करना (जैसे, विभिन्न आयु समूहों में खुशी के स्तर में क्या अंतर है)।
## बड़े संख्याओं का नियम और केंद्रीय सीमा प्रमेय
सामान्य वितरण इतना महत्वपूर्ण क्यों है, इसका एक कारण **केंद्रीय सीमा प्रमेय** (central limit theorem) है। मान लें कि हमारे पास स्वतंत्र N मानों X1, ..., XN का एक बड़ा नमूना है, जिसे किसी भी वितरण से लिया गया है, जिसका औसत μ और विचरण σ2 है। फिर, पर्याप्त बड़े N के लिए (दूसरे शब्दों में, जब N→∞), ΣiXi का औसत सामान्य रूप से वितरित होगा, जिसका औसत μ और विचरण σ2/N होगा।
> केंद्रीय सीमा प्रमेय की एक और व्याख्या यह है कि यह कहता है कि किसी भी यादृच्छिक चर मानों के योग का औसत निकालने पर आप सामान्य वितरण प्राप्त करते हैं।
केंद्रीय सीमा प्रमेय से यह भी पता चलता है कि, जब N→∞, नमूना औसत के μ के बराबर होने की संभावना 1 हो जाती है। इसे **बड़े संख्याओं का नियम** (law of large numbers) कहा जाता है।
## सहसंबंध और सहभिन्नता
डेटा साइंस का एक काम डेटा के बीच संबंध खोजना है। हम कहते हैं कि दो अनुक्रम **सहसंबद्ध** (correlate) हैं जब वे एक ही समय में समान व्यवहार प्रदर्शित करते हैं, यानी वे या तो एक साथ बढ़ते/घटते हैं, या एक अनुक्रम बढ़ता है जब दूसरा घटता है और इसके विपरीत। दूसरे शब्दों में, ऐसा लगता है कि दो अनुक्रमों के बीच कुछ संबंध है।
> सहसंबंध जरूरी नहीं कि दो अनुक्रमों के बीच कारणात्मक संबंध को इंगित करता है; कभी-कभी दोनों चर किसी बाहरी कारण पर निर्भर हो सकते हैं, या यह केवल संयोग से हो सकता है कि दोनों अनुक्रम सहसंबद्ध हैं। हालांकि, मजबूत गणितीय सहसंबंध इस बात का अच्छा संकेत है कि दो चर किसी न किसी तरह से जुड़े हुए हैं।
गणितीय रूप से, दो यादृच्छिक चरों के बीच संबंध दिखाने वाली मुख्य अवधारणा **सहभिन्नता** (covariance) है, जिसे इस प्रकार गणना किया जाता है: Cov(X,Y) = **E**\[(X-**E**(X))(Y-**E**(Y))\]। हम दोनों चरों के उनके औसत मानों से विचलन की गणना करते हैं, और फिर उन विचलनों के गुणनफल को लेते हैं। यदि दोनों चर एक साथ विचलित होते हैं, तो गुणनफल हमेशा एक सकारात्मक मान होगा, जो सकारात्मक सहभिन्नता में जुड़ जाएगा। यदि दोनों चर असंगत रूप से विचलित होते हैं (यानी एक औसत से नीचे गिरता है जब दूसरा औसत से ऊपर उठता है), तो हमें हमेशा नकारात्मक संख्याएँ मिलेंगी, जो नकारात्मक सहभिन्नता में जुड़ेंगी। यदि विचलन स्वतंत्र हैं, तो वे लगभग शून्य में जुड़ेंगे।
सहभिन्नता का परिमाण हमें यह नहीं बताता कि सहसंबंध कितना बड़ा है, क्योंकि यह वास्तविक मानों के परिमाण पर निर्भर करता है। इसे सामान्यीकृत करने के लिए, हम सहभिन्नता को दोनों चरों के मानक विचलन से विभाजित कर सकते हैं, ताकि **सहसंबंध** प्राप्त हो। अच्छी बात यह है कि सहसंबंध हमेशा [-1,1] की सीमा में होता है, जहां 1 मानों के बीच मजबूत सकारात्मक सहसंबंध को इंगित करता है, -1 - मजबूत नकारात्मक सहसंबंध, और 0 - बिल्कुल भी सहसंबंध नहीं (चर स्वतंत्र हैं)।
**उदाहरण**: हम ऊपर उल्लिखित बेसबॉल खिलाड़ियों के डेटासेट से वज़न और ऊंचाई के बीच सहसंबंध की गणना कर सकते हैं:
```python
print(np.corrcoef(weights,heights))
```
परिणामस्वरूप, हमें इस प्रकार का **सहसंबंध मैट्रिक्स** मिलता है:
```
array([[1. , 0.52959196],
[0.52959196, 1. ]])
```
> सहसंबंध मैट्रिक्स C किसी भी संख्या के इनपुट अनुक्रमों S1, ..., Sn के लिए गणना की जा सकती है। Cij का मान Si और Sj के बीच सहसंबंध है, और विकर्ण तत्व हमेशा 1 होते हैं (जो Si का आत्म-सहसंबंध भी है)।
हमारे मामले में, मान 0.53 इंगित करता है कि किसी व्यक्ति के वज़न और ऊंचाई के बीच कुछ सहसंबंध है। हम एक मान को दूसरे के खिलाफ बिखराव प्लॉट भी बना सकते हैं ताकि संबंध को दृश्य रूप से देखा जा सके:

> सहसंबंध और सहभिन्नता के और उदाहरण [संबंधित नोटबुक](notebook.ipynb) में पाए जा सकते हैं।
## निष्कर्ष
इस खंड में, हमने सीखा:
* डेटा के बुनियादी सांख्यिकीय गुण, जैसे औसत, विचरण, माध्यिका और चतुर्थांश
* यादृच्छिक चरों के विभिन्न वितरण, जिसमें सामान्य वितरण शामिल है
* विभिन्न गुणों के बीच सहसंबंध कैसे खोजें
* कुछ परिकल्पनाओं को साबित करने के लिए गणित और सांख्यिकी के सटीक उपकरणों का उपयोग कैसे करें
* दिए गए डेटा नमूने के लिए यादृच्छिक चर के विश्वास अंतराल की गणना कैसे करें
हालांकि यह संभावना और सांख्यिकी के भीतर मौजूद विषयों की पूरी सूची नहीं है, यह इस पाठ्यक्रम में एक अच्छी शुरुआत देने के लिए पर्याप्त होना चाहिए।
## 🚀 चुनौती
नोटबुक में दिए गए नमूना कोड का उपयोग करके अन्य परिकल्पनाओं का परीक्षण करें:
1. फर्स्ट बेसमैन सेकंड बेसमैन से बड़े हैं।
2. फर्स्ट बेसमैन थर्ड बेसमैन से ऊंचे हैं।
3. शॉर्टस्टॉप सेकंड बेसमैन से ऊंचे हैं।
## [पाठ के बाद क्विज़](https://ff-quizzes.netlify.app/en/ds/quiz/7)
## समीक्षा और स्व-अध्ययन
संभाव्यता और सांख्यिकी इतना व्यापक विषय है कि यह अपने स्वयं के पाठ्यक्रम के योग्य है। यदि आप सिद्धांत में गहराई तक जाना चाहते हैं, तो आप निम्नलिखित पुस्तकों को पढ़ना जारी रख सकते हैं:
1. [कार्लोस फर्नांडीज-ग्रांडा](https://cims.nyu.edu/~cfgranda/) न्यूयॉर्क विश्वविद्यालय से, जिनके पास [डेटा साइंस के लिए संभावना और सांख्यिकी](https://cims.nyu.edu/~cfgranda/pages/stuff/probability_stats_for_DS.pdf) पर शानदार व्याख्यान नोट्स हैं (ऑनलाइन उपलब्ध)।
2. [पीटर और एंड्रयू ब्रूस। डेटा वैज्ञानिकों के लिए व्यावहारिक सांख्यिकी।](https://www.oreilly.com/library/view/practical-statistics-for/9781491952955/) [[R में नमूना कोड](https://github.com/andrewgbruce/statistics-for-data-scientists)]।
3. [जेम्स डी. मिलर। डेटा साइंस के लिए सांख्यिकी](https://www.packtpub.com/product/statistics-for-data-science/9781788290678) [[R में नमूना कोड](https://github.com/PacktPublishing/Statistics-for-Data-Science)]।
## असाइनमेंट
[छोटा डायबिटीज़ अध्ययन](assignment.md)
## क्रेडिट्स
यह पाठ [दिमित्री सॉश्निकोव](http://soshnikov.com) द्वारा ♥️ के साथ लिखा गया है।
---
**अस्वीकरण**:
यह दस्तावेज़ AI अनुवाद सेवा [Co-op Translator](https://github.com/Azure/co-op-translator) का उपयोग करके अनुवादित किया गया है। जबकि हम सटीकता के लिए प्रयास करते हैं, कृपया ध्यान दें कि स्वचालित अनुवाद में त्रुटियां या अशुद्धियां हो सकती हैं। मूल भाषा में उपलब्ध मूल दस्तावेज़ को आधिकारिक स्रोत माना जाना चाहिए। महत्वपूर्ण जानकारी के लिए, पेशेवर मानव अनुवाद की सिफारिश की जाती है। इस अनुवाद के उपयोग से उत्पन्न किसी भी गलतफहमी या गलत व्याख्या के लिए हम उत्तरदायी नहीं हैं।
यहां हम **इंटर-क्वारटाइल रेंज** IQR=Q3-Q1 और तथाकथित **आउटलायर्स** - मान जो [Q1-1.5*IQR,Q3+1.5*IQR] की सीमाओं के बाहर होते हैं, की भी गणना करते हैं।
एक सीमित वितरण जिसमें संभावित मानों की संख्या कम होती है, एक अच्छा "विशिष्ट" मान वह होता है जो सबसे अधिक बार प्रकट होता है, जिसे **मोड** कहा जाता है। इसे अक्सर श्रेणीबद्ध डेटा, जैसे रंगों, पर लागू किया जाता है। मान लें कि हमारे पास दो समूह हैं - कुछ जो लाल रंग को पसंद करते हैं और अन्य जो नीले रंग को पसंद करते हैं। यदि हम रंगों को संख्याओं द्वारा कोड करते हैं, तो पसंदीदा रंग के लिए माध्य मान कहीं नारंगी-हरे स्पेक्ट्रम में होगा, जो किसी भी समूह की वास्तविक प्राथमिकता को इंगित नहीं करता। हालांकि, मोड या तो एक रंग होगा, या दोनों रंग होंगे, यदि उनके लिए मतदान करने वाले लोगों की संख्या समान है (इस मामले में हम नमूने को **मल्टीमोडल** कहते हैं)।
## वास्तविक दुनिया का डेटा
जब हम वास्तविक जीवन के डेटा का विश्लेषण करते हैं, तो वे अक्सर रैंडम वेरिएबल्स के रूप में नहीं होते हैं, इस अर्थ में कि हम अज्ञात परिणामों के साथ प्रयोग नहीं करते। उदाहरण के लिए, बेसबॉल खिलाड़ियों की एक टीम पर विचार करें, और उनके शरीर के डेटा, जैसे ऊंचाई, वजन और उम्र। ये संख्याएं बिल्कुल रैंडम नहीं हैं, लेकिन हम अभी भी उन्हीं गणितीय अवधारणाओं को लागू कर सकते हैं। उदाहरण के लिए, लोगों के वजन का अनुक्रम कुछ रैंडम वेरिएबल से लिए गए मानों का अनुक्रम माना जा सकता है। नीचे [मेजर लीग बेसबॉल](http://mlb.mlb.com/index.jsp) के वास्तविक बेसबॉल खिलाड़ियों के वजन का अनुक्रम दिया गया है, जो [इस डेटासेट](http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_MLB_HeightsWeights) से लिया गया है (आपकी सुविधा के लिए केवल पहले 20 मान दिखाए गए हैं):
```
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
```
> **नोट**: इस डेटासेट के साथ काम करने के उदाहरण को देखने के लिए, [संबंधित नोटबुक](notebook.ipynb) देखें। इस पाठ में कई चुनौतियां भी हैं, और आप उस नोटबुक में कुछ कोड जोड़कर उन्हें पूरा कर सकते हैं। यदि आप डेटा पर काम करने के तरीके के बारे में सुनिश्चित नहीं हैं, तो चिंता न करें - हम बाद में Python का उपयोग करके डेटा पर काम करने पर वापस आएंगे। यदि आप Jupyter Notebook में कोड चलाने का तरीका नहीं जानते हैं, तो [इस लेख](https://soshnikov.com/education/how-to-execute-notebooks-from-github/) को देखें।
यहां हमारे डेटा के लिए माध्य, माध्यिका और क्वारटाइल्स दिखाने वाला बॉक्स प्लॉट है:

चूंकि हमारे डेटा में विभिन्न खिलाड़ी **भूमिकाओं** की जानकारी है, हम भूमिका के अनुसार भी बॉक्स प्लॉट बना सकते हैं - यह हमें यह विचार करने की अनुमति देगा कि भूमिकाओं के बीच पैरामीटर मान कैसे भिन्न होते हैं। इस बार हम ऊंचाई पर विचार करेंगे:

यह आरेख सुझाव देता है कि, औसतन, पहले बेसमैन की ऊंचाई दूसरे बेसमैन की ऊंचाई से अधिक है। इस पाठ में बाद में हम सीखेंगे कि इस परिकल्पना को अधिक औपचारिक रूप से कैसे परीक्षण किया जा सकता है, और यह प्रदर्शित करने के लिए कि हमारे डेटा सांख्यिकीय रूप से महत्वपूर्ण है।
> जब वास्तविक दुनिया के डेटा के साथ काम करते हैं, तो हम मानते हैं कि सभी डेटा पॉइंट्स कुछ संभाव्यता वितरण से लिए गए नमूने हैं। यह धारणा हमें मशीन लर्निंग तकनीकों को लागू करने और काम करने वाले भविष्यवाणी मॉडल बनाने की अनुमति देती है।
हमारे डेटा का वितरण कैसा है, यह देखने के लिए हम **हिस्टोग्राम** नामक एक ग्राफ़ बना सकते हैं। X-अक्ष में विभिन्न वजन अंतराल (जिसे **बिन्स** कहा जाता है) की संख्या होगी, और वर्टिकल अक्ष दिखाएगा कि हमारा रैंडम वेरिएबल नमूना दिए गए अंतराल में कितनी बार था।

इस हिस्टोग्राम से आप देख सकते हैं कि सभी मान एक निश्चित माध्य वजन के आसपास केंद्रित हैं, और जैसे-जैसे हम उस वजन से दूर जाते हैं - उस मान के वजन कम बार मिलते हैं। यानी, यह बहुत ही असंभावित है कि बेसबॉल खिलाड़ी का वजन माध्य वजन से बहुत अलग होगा। वजन का विचरण दिखाता है कि वजन माध्य से कितना भिन्न होने की संभावना है।
> यदि हम अन्य लोगों के वजन लेते हैं, जो बेसबॉल लीग से नहीं हैं, तो वितरण अलग होने की संभावना है। हालांकि, वितरण का आकार समान रहेगा, लेकिन माध्य और विचरण बदल जाएंगे। इसलिए, यदि हम अपने मॉडल को बेसबॉल खिलाड़ियों पर प्रशिक्षित करते हैं, तो यह विश्वविद्यालय के छात्रों पर लागू होने पर गलत परिणाम देने की संभावना है, क्योंकि अंतर्निहित वितरण अलग है।
## नॉर्मल वितरण
ऊपर हमने जो वजन का वितरण देखा वह बहुत सामान्य है, और वास्तविक दुनिया से कई माप एक ही प्रकार के वितरण का पालन करते हैं, लेकिन अलग-अलग माध्य और विचरण के साथ। इस वितरण को **नॉर्मल वितरण** कहा जाता है, और यह सांख्यिकी में बहुत महत्वपूर्ण भूमिका निभाता है।
नॉर्मल वितरण का उपयोग संभावित बेसबॉल खिलाड़ियों के रैंडम वजन उत्पन्न करने का सही तरीका है। एक बार जब हम माध्य वजन `mean` और मानक विचलन `std` जानते हैं, तो हम निम्नलिखित तरीके से 1000 वजन नमूने उत्पन्न कर सकते हैं:
```python
samples = np.random.normal(mean,std,1000)
```
यदि हम उत्पन्न नमूनों का हिस्टोग्राम बनाते हैं, तो हम ऊपर दिखाए गए चित्र के समान चित्र देखेंगे। और यदि हम नमूनों की संख्या और बिन्स की संख्या बढ़ाते हैं, तो हम नॉर्मल वितरण की एक अधिक आदर्श तस्वीर उत्पन्न कर सकते हैं:

*माध्य=0 और मानक विचलन=1 के साथ नॉर्मल वितरण*
## विश्वास अंतराल
जब हम बेसबॉल खिलाड़ियों के वजन के बारे में बात करते हैं, तो हम मानते हैं कि एक निश्चित **रैंडम वेरिएबल W** है जो सभी बेसबॉल खिलाड़ियों के वजन के आदर्श संभाव्यता वितरण (जिसे **जनसंख्या** कहा जाता है) से मेल खाता है। हमारे वजन का अनुक्रम सभी बेसबॉल खिलाड़ियों के एक उपसमुच्चय से मेल खाता है जिसे हम **नमूना** कहते हैं। एक दिलचस्प सवाल यह है कि क्या हम W के वितरण के पैरामीटर, यानी जनसंख्या के माध्य और विचरण को जान सकते हैं?
सबसे आसान उत्तर होगा हमारे नमूने के माध्य और विचरण की गणना करना। हालांकि, ऐसा हो सकता है कि हमारा रैंडम नमूना पूरी जनसंख्या का सटीक प्रतिनिधित्व न करे। इसलिए **विश्वास अंतराल** के बारे में बात करना समझ में आता है।
> **विश्वास अंतराल** हमारे नमूने को देखते हुए जनसंख्या के वास्तविक माध्य का अनुमान है, जो एक निश्चित संभावना (या **विश्वास स्तर**) में सटीक है।
मान लें कि हमारे पास एक नमूना X
1, ..., Xn को हमारे वितरण से चुना गया है। हर बार जब हम अपने वितरण से एक नमूना लेते हैं, तो हमें अलग-अलग औसत मान μ प्राप्त होगा। इसलिए μ को एक यादृच्छिक चर माना जा सकता है। एक **विश्वास अंतराल** (confidence interval) जिसमें विश्वास p है, वह दो मानों (Lp,Rp) का एक युग्म है, ऐसा कि **P**(Lp≤μ≤Rp) = p, यानी मापा गया औसत मान इस अंतराल में आने की संभावना p के बराबर है।
यह हमारी छोटी सी भूमिका से परे है कि हम विस्तार से चर्चा करें कि इन विश्वास अंतरालों की गणना कैसे की जाती है। कुछ और विवरण [विकिपीडिया](https://en.wikipedia.org/wiki/Confidence_interval) पर पाए जा सकते हैं। संक्षेप में, हम वास्तविक जनसंख्या औसत के सापेक्ष गणना किए गए नमूना औसत के वितरण को परिभाषित करते हैं, जिसे **स्टूडेंट वितरण** (student distribution) कहा जाता है।
> **रोचक तथ्य**: स्टूडेंट वितरण का नाम गणितज्ञ विलियम सीली गॉसेट के नाम पर रखा गया है, जिन्होंने "स्टूडेंट" उपनाम के तहत अपना पेपर प्रकाशित किया। वे गिनीज ब्रुअरी में काम करते थे, और एक संस्करण के अनुसार, उनके नियोक्ता नहीं चाहते थे कि आम जनता को पता चले कि वे कच्चे माल की गुणवत्ता निर्धारित करने के लिए सांख्यिकीय परीक्षणों का उपयोग कर रहे थे।
यदि हम अपनी जनसंख्या के औसत μ का p विश्वास के साथ अनुमान लगाना चाहते हैं, तो हमें स्टूडेंट वितरण A का *(1-p)/2-थ परसेंटाइल* लेना होगा, जिसे या तो तालिकाओं से लिया जा सकता है, या सांख्यिकीय सॉफ़्टवेयर (जैसे Python, R, आदि) के कुछ अंतर्निर्मित कार्यों का उपयोग करके कंप्यूटर पर गणना की जा सकती है। फिर μ के लिए अंतराल X±A*D/√n होगा, जहां X नमूने का प्राप्त औसत है, और D मानक विचलन है।
> **ध्यान दें**: हम [स्वतंत्रता की डिग्री](https://en.wikipedia.org/wiki/Degrees_of_freedom_(statistics)) की एक महत्वपूर्ण अवधारणा की चर्चा को भी छोड़ देते हैं, जो स्टूडेंट वितरण के संदर्भ में महत्वपूर्ण है। इस अवधारणा को गहराई से समझने के लिए आप सांख्यिकी पर अधिक पूर्ण पुस्तकों का संदर्भ ले सकते हैं।
वज़न और ऊंचाई के लिए विश्वास अंतराल की गणना का एक उदाहरण [संबंधित नोटबुक](notebook.ipynb) में दिया गया है।
| p | वज़न औसत |
|-----|-----------|
| 0.85 | 201.73±0.94 |
| 0.90 | 201.73±1.08 |
| 0.95 | 201.73±1.28 |
ध्यान दें कि विश्वास संभावना जितनी अधिक होती है, विश्वास अंतराल उतना ही चौड़ा होता है।
## परिकल्पना परीक्षण
हमारे बेसबॉल खिलाड़ियों के डेटासेट में, विभिन्न खिलाड़ी भूमिकाएँ हैं, जिन्हें नीचे सारांशित किया जा सकता है (कैसे यह तालिका गणना की गई है, यह देखने के लिए [संबंधित नोटबुक](notebook.ipynb) देखें):
| भूमिका | ऊंचाई | वज़न | संख्या |
|------|--------|--------|-------|
| कैचर | 72.723684 | 204.328947 | 76 |
| डिज़िग्नेटेड हिटर | 74.222222 | 220.888889 | 18 |
| फर्स्ट बेसमैन | 74.000000 | 213.109091 | 55 |
| आउटफील्डर | 73.010309 | 199.113402 | 194 |
| रिलीफ पिचर | 74.374603 | 203.517460 | 315 |
| सेकंड बेसमैन | 71.362069 | 184.344828 | 58 |
| शॉर्टस्टॉप | 71.903846 | 182.923077 | 52 |
| स्टार्टिंग पिचर | 74.719457 | 205.163636 | 221 |
| थर्ड बेसमैन | 73.044444 | 200.955556 | 45 |
हम देख सकते हैं कि फर्स्ट बेसमैन की औसत ऊंचाई सेकंड बेसमैन से अधिक है। इसलिए, हम यह निष्कर्ष निकालने के लिए प्रेरित हो सकते हैं कि **फर्स्ट बेसमैन सेकंड बेसमैन से ऊंचे होते हैं**।
> इस कथन को **एक परिकल्पना** कहा जाता है, क्योंकि हमें नहीं पता कि यह तथ्य वास्तव में सत्य है या नहीं।
हालांकि, यह हमेशा स्पष्ट नहीं होता कि हम यह निष्कर्ष निकाल सकते हैं या नहीं। ऊपर की चर्चा से हमें पता है कि प्रत्येक औसत का एक संबंधित विश्वास अंतराल होता है, और इसलिए यह अंतर केवल एक सांख्यिकीय त्रुटि हो सकता है। हमें अपनी परिकल्पना का परीक्षण करने के लिए कुछ अधिक औपचारिक तरीके की आवश्यकता है।
आइए फर्स्ट और सेकंड बेसमैन की ऊंचाई के लिए विश्वास अंतराल को अलग-अलग गणना करें:
| विश्वास | फर्स्ट बेसमैन | सेकंड बेसमैन |
|------------|---------------|----------------|
| 0.85 | 73.62..74.38 | 71.04..71.69 |
| 0.90 | 73.56..74.44 | 70.99..71.73 |
| 0.95 | 73.47..74.53 | 70.92..71.81 |
हम देख सकते हैं कि किसी भी विश्वास स्तर पर अंतराल ओवरलैप नहीं करते। यह हमारी परिकल्पना को साबित करता है कि फर्स्ट बेसमैन सेकंड बेसमैन से ऊंचे होते हैं।
औपचारिक रूप से, हम जो समस्या हल कर रहे हैं वह यह देखना है कि **दो संभाव्यता वितरण समान हैं या नहीं**, या कम से कम उनके मापदंड समान हैं। वितरण के आधार पर, हमें इसके लिए अलग-अलग परीक्षणों का उपयोग करना होगा। यदि हमें पता है कि हमारे वितरण सामान्य हैं, तो हम **[स्टूडेंट t-परीक्षण](https://en.wikipedia.org/wiki/Student%27s_t-test)** लागू कर सकते हैं।
स्टूडेंट t-परीक्षण में, हम तथाकथित **t-मूल्य** की गणना करते हैं, जो औसतों के बीच के अंतर को, विचलन को ध्यान में रखते हुए, इंगित करता है। यह प्रदर्शित किया गया है कि t-मूल्य **स्टूडेंट वितरण** का अनुसरण करता है, जो हमें दिए गए विश्वास स्तर **p** के लिए सीमा मान प्राप्त करने की अनुमति देता है (यह गणना की जा सकती है, या संख्यात्मक तालिकाओं में देखा जा सकता है)। फिर हम t-मूल्य की तुलना इस सीमा से करते हैं ताकि परिकल्पना को स्वीकार या अस्वीकार कर सकें।
Python में, हम **SciPy** पैकेज का उपयोग कर सकते हैं, जिसमें `ttest_ind` फ़ंक्शन शामिल है (साथ ही कई अन्य उपयोगी सांख्यिकीय फ़ंक्शन!)। यह हमारे लिए t-मूल्य की गणना करता है, और विश्वास p-मूल्य का रिवर्स लुकअप भी करता है, ताकि हम केवल विश्वास को देखकर निष्कर्ष निकाल सकें।
उदाहरण के लिए, फर्स्ट और सेकंड बेसमैन की ऊंचाई की तुलना हमें निम्नलिखित परिणाम देती है:
```python
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
```
```
T-value = 7.65
P-value: 9.137321189738925e-12
```
हमारे मामले में, p-मूल्य बहुत कम है, जिसका अर्थ है कि फर्स्ट बेसमैन के ऊंचे होने का मजबूत प्रमाण है।
इसके अलावा, अन्य प्रकार की परिकल्पनाएँ भी हो सकती हैं जिन्हें हम परीक्षण करना चाह सकते हैं, जैसे:
* यह साबित करना कि कोई दिया गया नमूना किसी वितरण का अनुसरण करता है। हमारे मामले में हमने मान लिया है कि ऊंचाई सामान्य रूप से वितरित है, लेकिन इसे औपचारिक सांख्यिकीय सत्यापन की आवश्यकता है।
* यह साबित करना कि किसी नमूने का औसत मान किसी पूर्वनिर्धारित मान से मेल खाता है।
* कई नमूनों के औसतों की तुलना करना (जैसे, विभिन्न आयु समूहों में खुशी के स्तर में क्या अंतर है)।
## बड़े संख्याओं का नियम और केंद्रीय सीमा प्रमेय
सामान्य वितरण इतना महत्वपूर्ण क्यों है, इसका एक कारण **केंद्रीय सीमा प्रमेय** (central limit theorem) है। मान लें कि हमारे पास स्वतंत्र N मानों X1, ..., XN का एक बड़ा नमूना है, जिसे किसी भी वितरण से लिया गया है, जिसका औसत μ और विचरण σ2 है। फिर, पर्याप्त बड़े N के लिए (दूसरे शब्दों में, जब N→∞), ΣiXi का औसत सामान्य रूप से वितरित होगा, जिसका औसत μ और विचरण σ2/N होगा।
> केंद्रीय सीमा प्रमेय की एक और व्याख्या यह है कि यह कहता है कि किसी भी यादृच्छिक चर मानों के योग का औसत निकालने पर आप सामान्य वितरण प्राप्त करते हैं।
केंद्रीय सीमा प्रमेय से यह भी पता चलता है कि, जब N→∞, नमूना औसत के μ के बराबर होने की संभावना 1 हो जाती है। इसे **बड़े संख्याओं का नियम** (law of large numbers) कहा जाता है।
## सहसंबंध और सहभिन्नता
डेटा साइंस का एक काम डेटा के बीच संबंध खोजना है। हम कहते हैं कि दो अनुक्रम **सहसंबद्ध** (correlate) हैं जब वे एक ही समय में समान व्यवहार प्रदर्शित करते हैं, यानी वे या तो एक साथ बढ़ते/घटते हैं, या एक अनुक्रम बढ़ता है जब दूसरा घटता है और इसके विपरीत। दूसरे शब्दों में, ऐसा लगता है कि दो अनुक्रमों के बीच कुछ संबंध है।
> सहसंबंध जरूरी नहीं कि दो अनुक्रमों के बीच कारणात्मक संबंध को इंगित करता है; कभी-कभी दोनों चर किसी बाहरी कारण पर निर्भर हो सकते हैं, या यह केवल संयोग से हो सकता है कि दोनों अनुक्रम सहसंबद्ध हैं। हालांकि, मजबूत गणितीय सहसंबंध इस बात का अच्छा संकेत है कि दो चर किसी न किसी तरह से जुड़े हुए हैं।
गणितीय रूप से, दो यादृच्छिक चरों के बीच संबंध दिखाने वाली मुख्य अवधारणा **सहभिन्नता** (covariance) है, जिसे इस प्रकार गणना किया जाता है: Cov(X,Y) = **E**\[(X-**E**(X))(Y-**E**(Y))\]। हम दोनों चरों के उनके औसत मानों से विचलन की गणना करते हैं, और फिर उन विचलनों के गुणनफल को लेते हैं। यदि दोनों चर एक साथ विचलित होते हैं, तो गुणनफल हमेशा एक सकारात्मक मान होगा, जो सकारात्मक सहभिन्नता में जुड़ जाएगा। यदि दोनों चर असंगत रूप से विचलित होते हैं (यानी एक औसत से नीचे गिरता है जब दूसरा औसत से ऊपर उठता है), तो हमें हमेशा नकारात्मक संख्याएँ मिलेंगी, जो नकारात्मक सहभिन्नता में जुड़ेंगी। यदि विचलन स्वतंत्र हैं, तो वे लगभग शून्य में जुड़ेंगे।
सहभिन्नता का परिमाण हमें यह नहीं बताता कि सहसंबंध कितना बड़ा है, क्योंकि यह वास्तविक मानों के परिमाण पर निर्भर करता है। इसे सामान्यीकृत करने के लिए, हम सहभिन्नता को दोनों चरों के मानक विचलन से विभाजित कर सकते हैं, ताकि **सहसंबंध** प्राप्त हो। अच्छी बात यह है कि सहसंबंध हमेशा [-1,1] की सीमा में होता है, जहां 1 मानों के बीच मजबूत सकारात्मक सहसंबंध को इंगित करता है, -1 - मजबूत नकारात्मक सहसंबंध, और 0 - बिल्कुल भी सहसंबंध नहीं (चर स्वतंत्र हैं)।
**उदाहरण**: हम ऊपर उल्लिखित बेसबॉल खिलाड़ियों के डेटासेट से वज़न और ऊंचाई के बीच सहसंबंध की गणना कर सकते हैं:
```python
print(np.corrcoef(weights,heights))
```
परिणामस्वरूप, हमें इस प्रकार का **सहसंबंध मैट्रिक्स** मिलता है:
```
array([[1. , 0.52959196],
[0.52959196, 1. ]])
```
> सहसंबंध मैट्रिक्स C किसी भी संख्या के इनपुट अनुक्रमों S1, ..., Sn के लिए गणना की जा सकती है। Cij का मान Si और Sj के बीच सहसंबंध है, और विकर्ण तत्व हमेशा 1 होते हैं (जो Si का आत्म-सहसंबंध भी है)।
हमारे मामले में, मान 0.53 इंगित करता है कि किसी व्यक्ति के वज़न और ऊंचाई के बीच कुछ सहसंबंध है। हम एक मान को दूसरे के खिलाफ बिखराव प्लॉट भी बना सकते हैं ताकि संबंध को दृश्य रूप से देखा जा सके:

> सहसंबंध और सहभिन्नता के और उदाहरण [संबंधित नोटबुक](notebook.ipynb) में पाए जा सकते हैं।
## निष्कर्ष
इस खंड में, हमने सीखा:
* डेटा के बुनियादी सांख्यिकीय गुण, जैसे औसत, विचरण, माध्यिका और चतुर्थांश
* यादृच्छिक चरों के विभिन्न वितरण, जिसमें सामान्य वितरण शामिल है
* विभिन्न गुणों के बीच सहसंबंध कैसे खोजें
* कुछ परिकल्पनाओं को साबित करने के लिए गणित और सांख्यिकी के सटीक उपकरणों का उपयोग कैसे करें
* दिए गए डेटा नमूने के लिए यादृच्छिक चर के विश्वास अंतराल की गणना कैसे करें
हालांकि यह संभावना और सांख्यिकी के भीतर मौजूद विषयों की पूरी सूची नहीं है, यह इस पाठ्यक्रम में एक अच्छी शुरुआत देने के लिए पर्याप्त होना चाहिए।
## 🚀 चुनौती
नोटबुक में दिए गए नमूना कोड का उपयोग करके अन्य परिकल्पनाओं का परीक्षण करें:
1. फर्स्ट बेसमैन सेकंड बेसमैन से बड़े हैं।
2. फर्स्ट बेसमैन थर्ड बेसमैन से ऊंचे हैं।
3. शॉर्टस्टॉप सेकंड बेसमैन से ऊंचे हैं।
## [पाठ के बाद क्विज़](https://ff-quizzes.netlify.app/en/ds/quiz/7)
## समीक्षा और स्व-अध्ययन
संभाव्यता और सांख्यिकी इतना व्यापक विषय है कि यह अपने स्वयं के पाठ्यक्रम के योग्य है। यदि आप सिद्धांत में गहराई तक जाना चाहते हैं, तो आप निम्नलिखित पुस्तकों को पढ़ना जारी रख सकते हैं:
1. [कार्लोस फर्नांडीज-ग्रांडा](https://cims.nyu.edu/~cfgranda/) न्यूयॉर्क विश्वविद्यालय से, जिनके पास [डेटा साइंस के लिए संभावना और सांख्यिकी](https://cims.nyu.edu/~cfgranda/pages/stuff/probability_stats_for_DS.pdf) पर शानदार व्याख्यान नोट्स हैं (ऑनलाइन उपलब्ध)।
2. [पीटर और एंड्रयू ब्रूस। डेटा वैज्ञानिकों के लिए व्यावहारिक सांख्यिकी।](https://www.oreilly.com/library/view/practical-statistics-for/9781491952955/) [[R में नमूना कोड](https://github.com/andrewgbruce/statistics-for-data-scientists)]।
3. [जेम्स डी. मिलर। डेटा साइंस के लिए सांख्यिकी](https://www.packtpub.com/product/statistics-for-data-science/9781788290678) [[R में नमूना कोड](https://github.com/PacktPublishing/Statistics-for-Data-Science)]।
## असाइनमेंट
[छोटा डायबिटीज़ अध्ययन](assignment.md)
## क्रेडिट्स
यह पाठ [दिमित्री सॉश्निकोव](http://soshnikov.com) द्वारा ♥️ के साथ लिखा गया है।
---
**अस्वीकरण**:
यह दस्तावेज़ AI अनुवाद सेवा [Co-op Translator](https://github.com/Azure/co-op-translator) का उपयोग करके अनुवादित किया गया है। जबकि हम सटीकता के लिए प्रयास करते हैं, कृपया ध्यान दें कि स्वचालित अनुवाद में त्रुटियां या अशुद्धियां हो सकती हैं। मूल भाषा में उपलब्ध मूल दस्तावेज़ को आधिकारिक स्रोत माना जाना चाहिए। महत्वपूर्ण जानकारी के लिए, पेशेवर मानव अनुवाद की सिफारिश की जाती है। इस अनुवाद के उपयोग से उत्पन्न किसी भी गलतफहमी या गलत व्याख्या के लिए हम उत्तरदायी नहीं हैं।