# Une brève introduction aux statistiques et probabilités
| ](../../sketchnotes/04-Statistics-Probability.png)|
|:---:|
| Statistiques et Probabilités - _Sketchnote par [@nitya](https://twitter.com/nitya)_ |
La théorie des statistiques et des probabilités sont deux domaines étroitement liés des mathématiques, très pertinents pour la science des données. Il est possible de travailler avec des données sans une connaissance approfondie des mathématiques, mais il est tout de même préférable de connaître au moins quelques concepts de base. Voici une courte introduction pour vous aider à démarrer.
[](https://youtu.be/Z5Zy85g4Yjw)
## [Quiz avant le cours](https://ff-quizzes.netlify.app/en/ds/quiz/6)
## Probabilité et variables aléatoires
**La probabilité** est un nombre compris entre 0 et 1 qui exprime à quel point un **événement** est probable. Elle est définie comme le nombre de résultats positifs (qui mènent à l'événement), divisé par le nombre total de résultats, en supposant que tous les résultats sont également probables. Par exemple, lorsque nous lançons un dé, la probabilité d'obtenir un nombre pair est de 3/6 = 0,5.
Lorsque nous parlons d'événements, nous utilisons des **variables aléatoires**. Par exemple, la variable aléatoire qui représente le nombre obtenu en lançant un dé prend des valeurs de 1 à 6. L'ensemble des nombres de 1 à 6 est appelé **espace d'échantillonnage**. Nous pouvons parler de la probabilité qu'une variable aléatoire prenne une certaine valeur, par exemple P(X=3)=1/6.
La variable aléatoire dans l'exemple précédent est appelée **discrète**, car elle possède un espace d'échantillonnage dénombrable, c'est-à-dire qu'il existe des valeurs distinctes qui peuvent être énumérées. Il existe des cas où l'espace d'échantillonnage est un intervalle de nombres réels ou l'ensemble complet des nombres réels. Ces variables sont appelées **continues**. Un bon exemple est l'heure d'arrivée d'un bus.
## Distribution de probabilité
Dans le cas des variables aléatoires discrètes, il est facile de décrire la probabilité de chaque événement par une fonction P(X). Pour chaque valeur *s* de l'espace d'échantillonnage *S*, elle donnera un nombre compris entre 0 et 1, de sorte que la somme de toutes les valeurs de P(X=s) pour tous les événements soit égale à 1.
La distribution discrète la plus connue est la **distribution uniforme**, dans laquelle il existe un espace d'échantillonnage de N éléments, avec une probabilité égale de 1/N pour chacun d'eux.
Il est plus difficile de décrire la distribution de probabilité d'une variable continue, avec des valeurs tirées d'un intervalle [a,b], ou de l'ensemble complet des nombres réels ℝ. Prenons l'exemple de l'heure d'arrivée d'un bus. En réalité, pour chaque heure d'arrivée exacte *t*, la probabilité qu'un bus arrive exactement à cette heure est de 0 !
> Vous savez maintenant que des événements avec une probabilité de 0 se produisent, et très souvent ! Au moins chaque fois qu'un bus arrive !
Nous ne pouvons parler que de la probabilité qu'une variable tombe dans un intervalle donné de valeurs, par exemple P(t1≤X2). Dans ce cas, la distribution de probabilité est décrite par une **fonction de densité de probabilité** p(x), telle que
 Ici, nous calculons également l'**étendue interquartile** IQR=Q3-Q1, et les **valeurs aberrantes** - des valeurs qui se situent en dehors des limites [Q1-1.5*IQR,Q3+1.5*IQR].
Pour une distribution finie contenant un petit nombre de valeurs possibles, une bonne valeur "typique" est celle qui apparaît le plus fréquemment, appelée **mode**. Elle est souvent appliquée aux données catégoriques, comme les couleurs. Prenons une situation où nous avons deux groupes de personnes - certains qui préfèrent fortement le rouge, et d'autres qui préfèrent le bleu. Si nous codons les couleurs par des nombres, la valeur moyenne pour une couleur préférée serait quelque part dans le spectre orange-vert, ce qui n'indique pas la préférence réelle d'aucun groupe. Cependant, le mode serait soit l'une des couleurs, soit les deux couleurs, si le nombre de personnes votant pour elles est égal (dans ce cas, nous appelons l'échantillon **multimodal**).
## Données du monde réel
Lorsque nous analysons des données provenant de la vie réelle, elles ne sont souvent pas des variables aléatoires en tant que telles, dans le sens où nous ne réalisons pas d'expériences avec un résultat inconnu. Par exemple, considérons une équipe de joueurs de baseball et leurs données corporelles, telles que la taille, le poids et l'âge. Ces nombres ne sont pas exactement aléatoires, mais nous pouvons tout de même appliquer les mêmes concepts mathématiques. Par exemple, une séquence de poids de personnes peut être considérée comme une séquence de valeurs tirées d'une variable aléatoire. Voici la séquence des poids de joueurs de baseball réels de la [Major League Baseball](http://mlb.mlb.com/index.jsp), tirée de [ce jeu de données](http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_MLB_HeightsWeights) (pour votre commodité, seuls les 20 premiers poids sont affichés) :
```
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
```
> **Note** : Pour voir un exemple de travail avec ce jeu de données, consultez le [notebook associé](notebook.ipynb). Il y a également un certain nombre de défis tout au long de cette leçon, et vous pouvez les compléter en ajoutant du code à ce notebook. Si vous ne savez pas comment manipuler des données, ne vous inquiétez pas - nous reviendrons sur le travail avec des données en utilisant Python plus tard. Si vous ne savez pas comment exécuter du code dans Jupyter Notebook, consultez [cet article](https://soshnikov.com/education/how-to-execute-notebooks-from-github/).
Voici le diagramme en boîte montrant la moyenne, la médiane et les quartiles pour nos données :
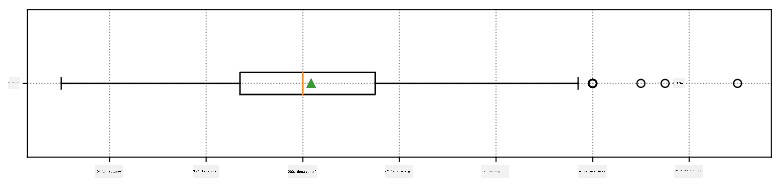
Étant donné que nos données contiennent des informations sur différents **rôles** de joueurs, nous pouvons également réaliser un diagramme en boîte par rôle - cela nous permettra de comprendre comment les valeurs des paramètres diffèrent selon les rôles. Cette fois, nous considérerons la taille :
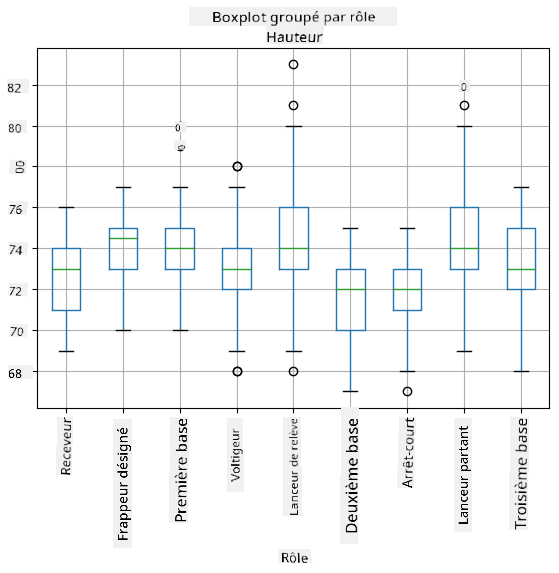
Ce diagramme suggère qu'en moyenne, la taille des joueurs de première base est supérieure à celle des joueurs de deuxième base. Plus tard dans cette leçon, nous apprendrons comment tester cette hypothèse de manière plus formelle et comment démontrer que nos données sont statistiquement significatives pour le prouver.
> Lorsque nous travaillons avec des données du monde réel, nous supposons que tous les points de données sont des échantillons tirés d'une certaine distribution de probabilité. Cette hypothèse nous permet d'appliquer des techniques d'apprentissage automatique et de construire des modèles prédictifs fonctionnels.
Pour voir quelle est la distribution de nos données, nous pouvons tracer un graphique appelé **histogramme**. L'axe X contiendra un certain nombre d'intervalles de poids différents (appelés **bins**), et l'axe vertical montrera le nombre de fois où notre échantillon de variable aléatoire se trouvait dans un intervalle donné.
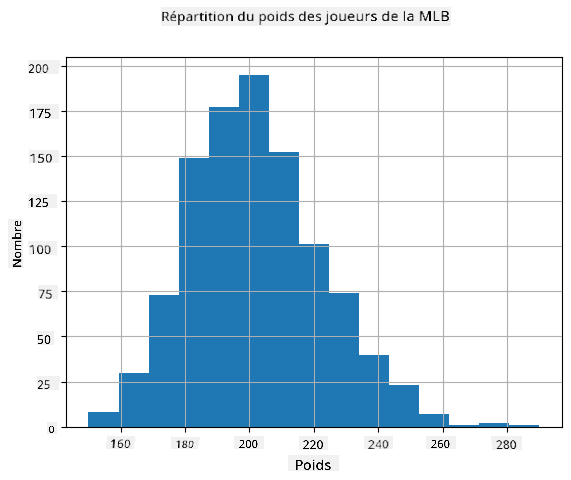
À partir de cet histogramme, vous pouvez voir que toutes les valeurs sont centrées autour d'un certain poids moyen, et plus nous nous éloignons de ce poids, moins nous rencontrons de poids de cette valeur. Autrement dit, il est très improbable que le poids d'un joueur de baseball soit très différent du poids moyen. La variance des poids montre dans quelle mesure les poids sont susceptibles de différer de la moyenne.
> Si nous prenons les poids d'autres personnes, pas de la ligue de baseball, la distribution sera probablement différente. Cependant, la forme de la distribution sera la même, mais la moyenne et la variance changeront. Ainsi, si nous entraînons notre modèle sur des joueurs de baseball, il est probable qu'il donne des résultats erronés lorsqu'il est appliqué à des étudiants d'une université, car la distribution sous-jacente est différente.
## Distribution normale
La distribution des poids que nous avons vue ci-dessus est très typique, et de nombreuses mesures du monde réel suivent le même type de distribution, mais avec des moyennes et des variances différentes. Cette distribution est appelée **distribution normale**, et elle joue un rôle très important en statistiques.
Utiliser la distribution normale est une manière correcte de générer des poids aléatoires de joueurs de baseball potentiels. Une fois que nous connaissons le poids moyen `mean` et l'écart-type `std`, nous pouvons générer 1000 échantillons de poids de la manière suivante :
```python
samples = np.random.normal(mean,std,1000)
```
Si nous traçons l'histogramme des échantillons générés, nous verrons une image très similaire à celle montrée ci-dessus. Et si nous augmentons le nombre d'échantillons et le nombre de bins, nous pouvons générer une image de distribution normale plus proche de l'idéal :
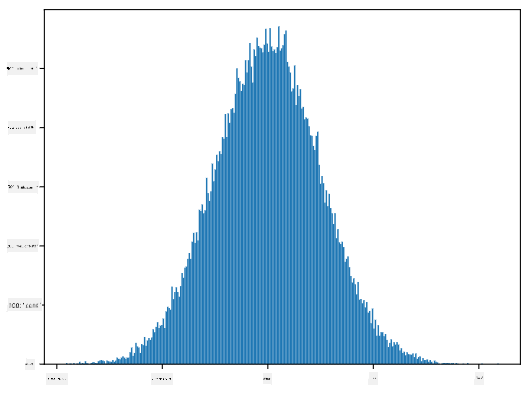
*Distribution normale avec moyenne=0 et écart-type=1*
## Intervalles de confiance
Lorsque nous parlons des poids des joueurs de baseball, nous supposons qu'il existe une certaine **variable aléatoire W** qui correspond à la distribution de probabilité idéale des poids de tous les joueurs de baseball (appelée **population**). Notre séquence de poids correspond à un sous-ensemble de tous les joueurs de baseball que nous appelons **échantillon**. Une question intéressante est : pouvons-nous connaître les paramètres de la distribution de W, c'est-à-dire la moyenne et la variance de la population ?
La réponse la plus simple serait de calculer la moyenne et la variance de notre échantillon. Cependant, il pourrait arriver que notre échantillon aléatoire ne représente pas précisément la population complète. Ainsi, il est logique de parler d'**intervalle de confiance**.
> **Intervalle de confiance** est l'estimation de la vraie moyenne de la population donnée notre échantillon, qui est précise avec une certaine probabilité (ou **niveau de confiance**).
Supposons que nous ayons un échantillon X
1, ..., Xn de notre distribution. Chaque fois que nous tirons un échantillon de notre distribution, nous obtenons une valeur moyenne μ différente. Ainsi, μ peut être considéré comme une variable aléatoire. Un **intervalle de confiance** avec une confiance p est une paire de valeurs (Lp,Rp), telle que **P**(Lp≤μ≤Rp) = p, c'est-à-dire qu'il y a une probabilité p que la valeur moyenne mesurée se situe dans l'intervalle.
Il dépasse le cadre de cette introduction de discuter en détail de la manière dont ces intervalles de confiance sont calculés. Vous pouvez trouver plus de détails [sur Wikipédia](https://fr.wikipedia.org/wiki/Intervalle_de_confiance). En résumé, nous définissons la distribution de la moyenne d'échantillon calculée par rapport à la vraie moyenne de la population, appelée **distribution de Student**.
> **Fait intéressant** : La distribution de Student porte le nom du mathématicien William Sealy Gosset, qui a publié son article sous le pseudonyme "Student". Il travaillait dans la brasserie Guinness et, selon une version, son employeur ne voulait pas que le grand public sache qu'ils utilisaient des tests statistiques pour évaluer la qualité des matières premières.
Si nous voulons estimer la moyenne μ de notre population avec une confiance p, nous devons prendre le *(1-p)/2-ème percentile* d'une distribution de Student A, qui peut être obtenu à partir de tables ou calculé à l'aide de fonctions intégrées dans des logiciels statistiques (par exemple Python, R, etc.). L'intervalle pour μ serait alors donné par X±A*D/√n, où X est la moyenne obtenue de l'échantillon, et D est l'écart-type.
> **Note** : Nous omettons également la discussion d'un concept important, celui des [degrés de liberté](https://fr.wikipedia.org/wiki/Degr%C3%A9s_de_libert%C3%A9_(statistiques)), qui est essentiel en relation avec la distribution de Student. Vous pouvez consulter des ouvrages plus complets sur les statistiques pour approfondir ce concept.
Un exemple de calcul d'intervalle de confiance pour les poids et les tailles est donné dans les [notebooks associés](notebook.ipynb).
| p | Moyenne du poids |
|------|------------------|
| 0.85 | 201,73±0,94 |
| 0.90 | 201,73±1,08 |
| 0.95 | 201,73±1,28 |
Remarquez que plus la probabilité de confiance est élevée, plus l'intervalle de confiance est large.
## Test d'hypothèses
Dans notre ensemble de données sur les joueurs de baseball, il existe différents rôles de joueurs, qui peuvent être résumés ci-dessous (consultez le [notebook associé](notebook.ipynb) pour voir comment ce tableau peut être calculé) :
| Rôle | Taille | Poids | Nombre |
|--------------------|----------|----------|--------|
| Receveur | 72,723684 | 204,328947 | 76 |
| Frappeur désigné | 74,222222 | 220,888889 | 18 |
| Premier but | 74,000000 | 213,109091 | 55 |
| Voltigeur | 73,010309 | 199,113402 | 194 |
| Lanceur de relève | 74,374603 | 203,517460 | 315 |
| Deuxième but | 71,362069 | 184,344828 | 58 |
| Arrêt-court | 71,903846 | 182,923077 | 52 |
| Lanceur partant | 74,719457 | 205,163636 | 221 |
| Troisième but | 73,044444 | 200,955556 | 45 |
Nous pouvons remarquer que la taille moyenne des premiers buts est supérieure à celle des deuxièmes buts. Ainsi, nous pourrions être tentés de conclure que **les premiers buts sont plus grands que les deuxièmes buts**.
> Cette affirmation est appelée **une hypothèse**, car nous ne savons pas si ce fait est réellement vrai ou non.
Cependant, il n'est pas toujours évident de pouvoir tirer cette conclusion. D'après la discussion précédente, nous savons que chaque moyenne est associée à un intervalle de confiance, et cette différence peut donc simplement être une erreur statistique. Nous avons besoin d'une méthode plus formelle pour tester notre hypothèse.
Calculons les intervalles de confiance séparément pour les tailles des premiers et deuxièmes buts :
| Confiance | Premiers buts | Deuxièmes buts |
|-----------|---------------|----------------|
| 0.85 | 73,62..74,38 | 71,04..71,69 |
| 0.90 | 73,56..74,44 | 70,99..71,73 |
| 0.95 | 73,47..74,53 | 70,92..71,81 |
Nous pouvons voir qu'à aucun niveau de confiance les intervalles ne se chevauchent. Cela prouve notre hypothèse selon laquelle les premiers buts sont plus grands que les deuxièmes buts.
Plus formellement, le problème que nous résolvons est de voir si **deux distributions de probabilité sont identiques**, ou du moins ont les mêmes paramètres. Selon la distribution, nous devons utiliser différents tests pour cela. Si nous savons que nos distributions sont normales, nous pouvons appliquer le **[test t de Student](https://fr.wikipedia.org/wiki/Test_t_de_Student)**.
Dans le test t de Student, nous calculons ce qu'on appelle la **valeur t**, qui indique la différence entre les moyennes en tenant compte de la variance. Il est démontré que la valeur t suit une **distribution de Student**, ce qui nous permet d'obtenir la valeur seuil pour un niveau de confiance donné **p** (cela peut être calculé ou consulté dans des tables numériques). Nous comparons ensuite la valeur t à ce seuil pour approuver ou rejeter l'hypothèse.
En Python, nous pouvons utiliser le package **SciPy**, qui inclut la fonction `ttest_ind` (en plus de nombreuses autres fonctions statistiques utiles !). Cette fonction calcule la valeur t pour nous et effectue également la recherche inverse de la valeur de confiance p, de sorte que nous pouvons simplement examiner la confiance pour tirer une conclusion.
Par exemple, notre comparaison entre les tailles des premiers et deuxièmes buts nous donne les résultats suivants :
```python
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
```
```
T-value = 7.65
P-value: 9.137321189738925e-12
```
Dans notre cas, la valeur p est très faible, ce qui signifie qu'il existe des preuves solides soutenant que les premiers buts sont plus grands.
Il existe également d'autres types d'hypothèses que nous pourrions vouloir tester, par exemple :
* Prouver qu'un échantillon donné suit une distribution spécifique. Dans notre cas, nous avons supposé que les tailles sont distribuées normalement, mais cela nécessite une vérification statistique formelle.
* Prouver qu'une valeur moyenne d'un échantillon correspond à une valeur prédéfinie.
* Comparer les moyennes de plusieurs échantillons (par exemple, quelle est la différence des niveaux de bonheur entre différents groupes d'âge).
## Loi des grands nombres et théorème central limite
L'une des raisons pour lesquelles la distribution normale est si importante est le **théorème central limite**. Supposons que nous ayons un grand échantillon de N valeurs indépendantes X1, ..., XN, échantillonnées à partir de n'importe quelle distribution avec une moyenne μ et une variance σ2. Alors, pour un N suffisamment grand (en d'autres termes, lorsque N→∞), la moyenne ΣiXi sera distribuée normalement, avec une moyenne μ et une variance σ2/N.
> Une autre façon d'interpréter le théorème central limite est de dire que, quelle que soit la distribution, lorsque vous calculez la moyenne d'une somme de valeurs de variables aléatoires, vous obtenez une distribution normale.
D'après le théorème central limite, il s'ensuit également que, lorsque N→∞, la probabilité que la moyenne de l'échantillon soit égale à μ devient 1. Cela est connu sous le nom de **loi des grands nombres**.
## Covariance et corrélation
L'une des tâches de la science des données est de trouver des relations entre les données. Nous disons que deux séries **corrèlent** lorsqu'elles présentent un comportement similaire au même moment, c'est-à-dire qu'elles augmentent/diminuent simultanément, ou qu'une série augmente lorsque l'autre diminue, et vice versa. En d'autres termes, il semble y avoir une relation entre les deux séries.
> La corrélation n'indique pas nécessairement une relation causale entre deux séries ; parfois, les deux variables peuvent dépendre d'une cause externe, ou il peut s'agir d'une simple coïncidence. Cependant, une forte corrélation mathématique est une bonne indication que deux variables sont d'une certaine manière connectées.
Mathématiquement, le concept principal qui montre la relation entre deux variables aléatoires est la **covariance**, qui est calculée comme suit : Cov(X,Y) = **E**\[(X-**E**(X))(Y-**E**(Y))\]. Nous calculons l'écart des deux variables par rapport à leurs valeurs moyennes, puis le produit de ces écarts. Si les deux variables dévient ensemble, le produit sera toujours une valeur positive, ce qui donnera une covariance positive. Si les deux variables dévient de manière désynchronisée (c'est-à-dire qu'une diminue en dessous de la moyenne lorsque l'autre augmente au-dessus de la moyenne), nous obtiendrons toujours des nombres négatifs, ce qui donnera une covariance négative. Si les écarts ne sont pas dépendants, ils s'annuleront approximativement à zéro.
La valeur absolue de la covariance ne nous dit pas grand-chose sur l'ampleur de la corrélation, car elle dépend de la magnitude des valeurs réelles. Pour la normaliser, nous pouvons diviser la covariance par l'écart-type des deux variables, pour obtenir la **corrélation**. L'avantage est que la corrélation est toujours dans la plage de [-1,1], où 1 indique une forte corrélation positive entre les valeurs, -1 une forte corrélation négative, et 0 aucune corrélation (les variables sont indépendantes).
**Exemple** : Nous pouvons calculer la corrélation entre les poids et les tailles des joueurs de baseball à partir de l'ensemble de données mentionné ci-dessus :
```python
print(np.corrcoef(weights,heights))
```
En résultat, nous obtenons une **matrice de corrélation** comme celle-ci :
```
array([[1. , 0.52959196],
[0.52959196, 1. ]])
```
> La matrice de corrélation C peut être calculée pour n'importe quel nombre de séries d'entrée S1, ..., Sn. La valeur de Cij est la corrélation entre Si et Sj, et les éléments diagonaux sont toujours égaux à 1 (ce qui correspond également à l'auto-corrélation de Si).
Dans notre cas, la valeur 0,53 indique qu'il existe une certaine corrélation entre le poids et la taille d'une personne. Nous pouvons également tracer un nuage de points d'une valeur par rapport à l'autre pour voir visuellement la relation :
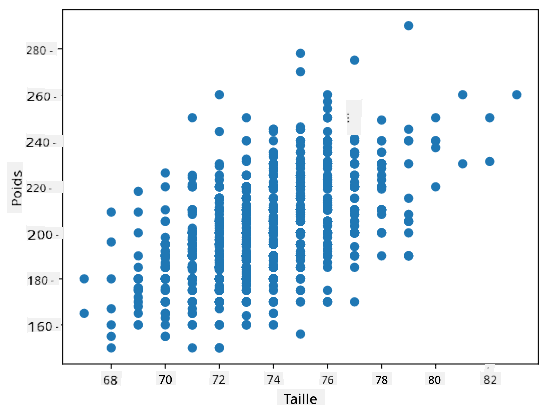
> Plus d'exemples de corrélation et de covariance peuvent être trouvés dans le [notebook associé](notebook.ipynb).
## Conclusion
Dans cette section, nous avons appris :
* les propriétés statistiques de base des données, telles que la moyenne, la variance, le mode et les quartiles
* les différentes distributions de variables aléatoires, y compris la distribution normale
* comment trouver la corrélation entre différentes propriétés
* comment utiliser des outils mathématiques et statistiques pour prouver certaines hypothèses
* comment calculer des intervalles de confiance pour une variable aléatoire à partir d'un échantillon de données
Bien que cette liste ne soit pas exhaustive des sujets existant dans les probabilités et les statistiques, elle devrait suffire à vous donner un bon départ dans ce cours.
## 🚀 Défi
Utilisez le code d'exemple dans le notebook pour tester d'autres hypothèses :
1. Les premiers buts sont plus âgés que les deuxièmes buts.
2. Les premiers buts sont plus grands que les troisièmes buts.
3. Les arrêts-courts sont plus grands que les deuxièmes buts.
## [Quiz post-cours](https://ff-quizzes.netlify.app/fr/ds/quiz/7)
## Révision et auto-apprentissage
Les probabilités et les statistiques sont un sujet si vaste qu'il mérite son propre cours. Si vous souhaitez approfondir la théorie, vous pouvez continuer à lire certains des livres suivants :
1. [Carlos Fernandez-Granda](https://cims.nyu.edu/~cfgranda/) de l'Université de New York propose d'excellentes notes de cours [Probability and Statistics for Data Science](https://cims.nyu.edu/~cfgranda/pages/stuff/probability_stats_for_DS.pdf) (disponibles en ligne).
1. [Peter et Andrew Bruce. Practical Statistics for Data Scientists.](https://www.oreilly.com/library/view/practical-statistics-for/9781491952955/) [[code d'exemple en R](https://github.com/andrewgbruce/statistics-for-data-scientists)].
1. [James D. Miller. Statistics for Data Science](https://www.packtpub.com/product/statistics-for-data-science/9781788290678) [[code d'exemple en R](https://github.com/PacktPublishing/Statistics-for-Data-Science)].
## Devoir
[Petite étude sur le diabète](assignment.md)
## Crédits
Cette leçon a été rédigée avec ♥️ par [Dmitry Soshnikov](http://soshnikov.com)
---
**Avertissement** :
Ce document a été traduit à l'aide du service de traduction automatique [Co-op Translator](https://github.com/Azure/co-op-translator). Bien que nous nous efforcions d'assurer l'exactitude, veuillez noter que les traductions automatisées peuvent contenir des erreurs ou des inexactitudes. Le document original dans sa langue d'origine doit être considéré comme la source faisant autorité. Pour des informations critiques, il est recommandé de faire appel à une traduction humaine professionnelle. Nous déclinons toute responsabilité en cas de malentendus ou d'interprétations erronées résultant de l'utilisation de cette traduction.
Ici, nous calculons également l'**étendue interquartile** IQR=Q3-Q1, et les **valeurs aberrantes** - des valeurs qui se situent en dehors des limites [Q1-1.5*IQR,Q3+1.5*IQR].
Pour une distribution finie contenant un petit nombre de valeurs possibles, une bonne valeur "typique" est celle qui apparaît le plus fréquemment, appelée **mode**. Elle est souvent appliquée aux données catégoriques, comme les couleurs. Prenons une situation où nous avons deux groupes de personnes - certains qui préfèrent fortement le rouge, et d'autres qui préfèrent le bleu. Si nous codons les couleurs par des nombres, la valeur moyenne pour une couleur préférée serait quelque part dans le spectre orange-vert, ce qui n'indique pas la préférence réelle d'aucun groupe. Cependant, le mode serait soit l'une des couleurs, soit les deux couleurs, si le nombre de personnes votant pour elles est égal (dans ce cas, nous appelons l'échantillon **multimodal**).
## Données du monde réel
Lorsque nous analysons des données provenant de la vie réelle, elles ne sont souvent pas des variables aléatoires en tant que telles, dans le sens où nous ne réalisons pas d'expériences avec un résultat inconnu. Par exemple, considérons une équipe de joueurs de baseball et leurs données corporelles, telles que la taille, le poids et l'âge. Ces nombres ne sont pas exactement aléatoires, mais nous pouvons tout de même appliquer les mêmes concepts mathématiques. Par exemple, une séquence de poids de personnes peut être considérée comme une séquence de valeurs tirées d'une variable aléatoire. Voici la séquence des poids de joueurs de baseball réels de la [Major League Baseball](http://mlb.mlb.com/index.jsp), tirée de [ce jeu de données](http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_MLB_HeightsWeights) (pour votre commodité, seuls les 20 premiers poids sont affichés) :
```
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
```
> **Note** : Pour voir un exemple de travail avec ce jeu de données, consultez le [notebook associé](notebook.ipynb). Il y a également un certain nombre de défis tout au long de cette leçon, et vous pouvez les compléter en ajoutant du code à ce notebook. Si vous ne savez pas comment manipuler des données, ne vous inquiétez pas - nous reviendrons sur le travail avec des données en utilisant Python plus tard. Si vous ne savez pas comment exécuter du code dans Jupyter Notebook, consultez [cet article](https://soshnikov.com/education/how-to-execute-notebooks-from-github/).
Voici le diagramme en boîte montrant la moyenne, la médiane et les quartiles pour nos données :

Étant donné que nos données contiennent des informations sur différents **rôles** de joueurs, nous pouvons également réaliser un diagramme en boîte par rôle - cela nous permettra de comprendre comment les valeurs des paramètres diffèrent selon les rôles. Cette fois, nous considérerons la taille :

Ce diagramme suggère qu'en moyenne, la taille des joueurs de première base est supérieure à celle des joueurs de deuxième base. Plus tard dans cette leçon, nous apprendrons comment tester cette hypothèse de manière plus formelle et comment démontrer que nos données sont statistiquement significatives pour le prouver.
> Lorsque nous travaillons avec des données du monde réel, nous supposons que tous les points de données sont des échantillons tirés d'une certaine distribution de probabilité. Cette hypothèse nous permet d'appliquer des techniques d'apprentissage automatique et de construire des modèles prédictifs fonctionnels.
Pour voir quelle est la distribution de nos données, nous pouvons tracer un graphique appelé **histogramme**. L'axe X contiendra un certain nombre d'intervalles de poids différents (appelés **bins**), et l'axe vertical montrera le nombre de fois où notre échantillon de variable aléatoire se trouvait dans un intervalle donné.

À partir de cet histogramme, vous pouvez voir que toutes les valeurs sont centrées autour d'un certain poids moyen, et plus nous nous éloignons de ce poids, moins nous rencontrons de poids de cette valeur. Autrement dit, il est très improbable que le poids d'un joueur de baseball soit très différent du poids moyen. La variance des poids montre dans quelle mesure les poids sont susceptibles de différer de la moyenne.
> Si nous prenons les poids d'autres personnes, pas de la ligue de baseball, la distribution sera probablement différente. Cependant, la forme de la distribution sera la même, mais la moyenne et la variance changeront. Ainsi, si nous entraînons notre modèle sur des joueurs de baseball, il est probable qu'il donne des résultats erronés lorsqu'il est appliqué à des étudiants d'une université, car la distribution sous-jacente est différente.
## Distribution normale
La distribution des poids que nous avons vue ci-dessus est très typique, et de nombreuses mesures du monde réel suivent le même type de distribution, mais avec des moyennes et des variances différentes. Cette distribution est appelée **distribution normale**, et elle joue un rôle très important en statistiques.
Utiliser la distribution normale est une manière correcte de générer des poids aléatoires de joueurs de baseball potentiels. Une fois que nous connaissons le poids moyen `mean` et l'écart-type `std`, nous pouvons générer 1000 échantillons de poids de la manière suivante :
```python
samples = np.random.normal(mean,std,1000)
```
Si nous traçons l'histogramme des échantillons générés, nous verrons une image très similaire à celle montrée ci-dessus. Et si nous augmentons le nombre d'échantillons et le nombre de bins, nous pouvons générer une image de distribution normale plus proche de l'idéal :

*Distribution normale avec moyenne=0 et écart-type=1*
## Intervalles de confiance
Lorsque nous parlons des poids des joueurs de baseball, nous supposons qu'il existe une certaine **variable aléatoire W** qui correspond à la distribution de probabilité idéale des poids de tous les joueurs de baseball (appelée **population**). Notre séquence de poids correspond à un sous-ensemble de tous les joueurs de baseball que nous appelons **échantillon**. Une question intéressante est : pouvons-nous connaître les paramètres de la distribution de W, c'est-à-dire la moyenne et la variance de la population ?
La réponse la plus simple serait de calculer la moyenne et la variance de notre échantillon. Cependant, il pourrait arriver que notre échantillon aléatoire ne représente pas précisément la population complète. Ainsi, il est logique de parler d'**intervalle de confiance**.
> **Intervalle de confiance** est l'estimation de la vraie moyenne de la population donnée notre échantillon, qui est précise avec une certaine probabilité (ou **niveau de confiance**).
Supposons que nous ayons un échantillon X
1, ..., Xn de notre distribution. Chaque fois que nous tirons un échantillon de notre distribution, nous obtenons une valeur moyenne μ différente. Ainsi, μ peut être considéré comme une variable aléatoire. Un **intervalle de confiance** avec une confiance p est une paire de valeurs (Lp,Rp), telle que **P**(Lp≤μ≤Rp) = p, c'est-à-dire qu'il y a une probabilité p que la valeur moyenne mesurée se situe dans l'intervalle.
Il dépasse le cadre de cette introduction de discuter en détail de la manière dont ces intervalles de confiance sont calculés. Vous pouvez trouver plus de détails [sur Wikipédia](https://fr.wikipedia.org/wiki/Intervalle_de_confiance). En résumé, nous définissons la distribution de la moyenne d'échantillon calculée par rapport à la vraie moyenne de la population, appelée **distribution de Student**.
> **Fait intéressant** : La distribution de Student porte le nom du mathématicien William Sealy Gosset, qui a publié son article sous le pseudonyme "Student". Il travaillait dans la brasserie Guinness et, selon une version, son employeur ne voulait pas que le grand public sache qu'ils utilisaient des tests statistiques pour évaluer la qualité des matières premières.
Si nous voulons estimer la moyenne μ de notre population avec une confiance p, nous devons prendre le *(1-p)/2-ème percentile* d'une distribution de Student A, qui peut être obtenu à partir de tables ou calculé à l'aide de fonctions intégrées dans des logiciels statistiques (par exemple Python, R, etc.). L'intervalle pour μ serait alors donné par X±A*D/√n, où X est la moyenne obtenue de l'échantillon, et D est l'écart-type.
> **Note** : Nous omettons également la discussion d'un concept important, celui des [degrés de liberté](https://fr.wikipedia.org/wiki/Degr%C3%A9s_de_libert%C3%A9_(statistiques)), qui est essentiel en relation avec la distribution de Student. Vous pouvez consulter des ouvrages plus complets sur les statistiques pour approfondir ce concept.
Un exemple de calcul d'intervalle de confiance pour les poids et les tailles est donné dans les [notebooks associés](notebook.ipynb).
| p | Moyenne du poids |
|------|------------------|
| 0.85 | 201,73±0,94 |
| 0.90 | 201,73±1,08 |
| 0.95 | 201,73±1,28 |
Remarquez que plus la probabilité de confiance est élevée, plus l'intervalle de confiance est large.
## Test d'hypothèses
Dans notre ensemble de données sur les joueurs de baseball, il existe différents rôles de joueurs, qui peuvent être résumés ci-dessous (consultez le [notebook associé](notebook.ipynb) pour voir comment ce tableau peut être calculé) :
| Rôle | Taille | Poids | Nombre |
|--------------------|----------|----------|--------|
| Receveur | 72,723684 | 204,328947 | 76 |
| Frappeur désigné | 74,222222 | 220,888889 | 18 |
| Premier but | 74,000000 | 213,109091 | 55 |
| Voltigeur | 73,010309 | 199,113402 | 194 |
| Lanceur de relève | 74,374603 | 203,517460 | 315 |
| Deuxième but | 71,362069 | 184,344828 | 58 |
| Arrêt-court | 71,903846 | 182,923077 | 52 |
| Lanceur partant | 74,719457 | 205,163636 | 221 |
| Troisième but | 73,044444 | 200,955556 | 45 |
Nous pouvons remarquer que la taille moyenne des premiers buts est supérieure à celle des deuxièmes buts. Ainsi, nous pourrions être tentés de conclure que **les premiers buts sont plus grands que les deuxièmes buts**.
> Cette affirmation est appelée **une hypothèse**, car nous ne savons pas si ce fait est réellement vrai ou non.
Cependant, il n'est pas toujours évident de pouvoir tirer cette conclusion. D'après la discussion précédente, nous savons que chaque moyenne est associée à un intervalle de confiance, et cette différence peut donc simplement être une erreur statistique. Nous avons besoin d'une méthode plus formelle pour tester notre hypothèse.
Calculons les intervalles de confiance séparément pour les tailles des premiers et deuxièmes buts :
| Confiance | Premiers buts | Deuxièmes buts |
|-----------|---------------|----------------|
| 0.85 | 73,62..74,38 | 71,04..71,69 |
| 0.90 | 73,56..74,44 | 70,99..71,73 |
| 0.95 | 73,47..74,53 | 70,92..71,81 |
Nous pouvons voir qu'à aucun niveau de confiance les intervalles ne se chevauchent. Cela prouve notre hypothèse selon laquelle les premiers buts sont plus grands que les deuxièmes buts.
Plus formellement, le problème que nous résolvons est de voir si **deux distributions de probabilité sont identiques**, ou du moins ont les mêmes paramètres. Selon la distribution, nous devons utiliser différents tests pour cela. Si nous savons que nos distributions sont normales, nous pouvons appliquer le **[test t de Student](https://fr.wikipedia.org/wiki/Test_t_de_Student)**.
Dans le test t de Student, nous calculons ce qu'on appelle la **valeur t**, qui indique la différence entre les moyennes en tenant compte de la variance. Il est démontré que la valeur t suit une **distribution de Student**, ce qui nous permet d'obtenir la valeur seuil pour un niveau de confiance donné **p** (cela peut être calculé ou consulté dans des tables numériques). Nous comparons ensuite la valeur t à ce seuil pour approuver ou rejeter l'hypothèse.
En Python, nous pouvons utiliser le package **SciPy**, qui inclut la fonction `ttest_ind` (en plus de nombreuses autres fonctions statistiques utiles !). Cette fonction calcule la valeur t pour nous et effectue également la recherche inverse de la valeur de confiance p, de sorte que nous pouvons simplement examiner la confiance pour tirer une conclusion.
Par exemple, notre comparaison entre les tailles des premiers et deuxièmes buts nous donne les résultats suivants :
```python
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
```
```
T-value = 7.65
P-value: 9.137321189738925e-12
```
Dans notre cas, la valeur p est très faible, ce qui signifie qu'il existe des preuves solides soutenant que les premiers buts sont plus grands.
Il existe également d'autres types d'hypothèses que nous pourrions vouloir tester, par exemple :
* Prouver qu'un échantillon donné suit une distribution spécifique. Dans notre cas, nous avons supposé que les tailles sont distribuées normalement, mais cela nécessite une vérification statistique formelle.
* Prouver qu'une valeur moyenne d'un échantillon correspond à une valeur prédéfinie.
* Comparer les moyennes de plusieurs échantillons (par exemple, quelle est la différence des niveaux de bonheur entre différents groupes d'âge).
## Loi des grands nombres et théorème central limite
L'une des raisons pour lesquelles la distribution normale est si importante est le **théorème central limite**. Supposons que nous ayons un grand échantillon de N valeurs indépendantes X1, ..., XN, échantillonnées à partir de n'importe quelle distribution avec une moyenne μ et une variance σ2. Alors, pour un N suffisamment grand (en d'autres termes, lorsque N→∞), la moyenne ΣiXi sera distribuée normalement, avec une moyenne μ et une variance σ2/N.
> Une autre façon d'interpréter le théorème central limite est de dire que, quelle que soit la distribution, lorsque vous calculez la moyenne d'une somme de valeurs de variables aléatoires, vous obtenez une distribution normale.
D'après le théorème central limite, il s'ensuit également que, lorsque N→∞, la probabilité que la moyenne de l'échantillon soit égale à μ devient 1. Cela est connu sous le nom de **loi des grands nombres**.
## Covariance et corrélation
L'une des tâches de la science des données est de trouver des relations entre les données. Nous disons que deux séries **corrèlent** lorsqu'elles présentent un comportement similaire au même moment, c'est-à-dire qu'elles augmentent/diminuent simultanément, ou qu'une série augmente lorsque l'autre diminue, et vice versa. En d'autres termes, il semble y avoir une relation entre les deux séries.
> La corrélation n'indique pas nécessairement une relation causale entre deux séries ; parfois, les deux variables peuvent dépendre d'une cause externe, ou il peut s'agir d'une simple coïncidence. Cependant, une forte corrélation mathématique est une bonne indication que deux variables sont d'une certaine manière connectées.
Mathématiquement, le concept principal qui montre la relation entre deux variables aléatoires est la **covariance**, qui est calculée comme suit : Cov(X,Y) = **E**\[(X-**E**(X))(Y-**E**(Y))\]. Nous calculons l'écart des deux variables par rapport à leurs valeurs moyennes, puis le produit de ces écarts. Si les deux variables dévient ensemble, le produit sera toujours une valeur positive, ce qui donnera une covariance positive. Si les deux variables dévient de manière désynchronisée (c'est-à-dire qu'une diminue en dessous de la moyenne lorsque l'autre augmente au-dessus de la moyenne), nous obtiendrons toujours des nombres négatifs, ce qui donnera une covariance négative. Si les écarts ne sont pas dépendants, ils s'annuleront approximativement à zéro.
La valeur absolue de la covariance ne nous dit pas grand-chose sur l'ampleur de la corrélation, car elle dépend de la magnitude des valeurs réelles. Pour la normaliser, nous pouvons diviser la covariance par l'écart-type des deux variables, pour obtenir la **corrélation**. L'avantage est que la corrélation est toujours dans la plage de [-1,1], où 1 indique une forte corrélation positive entre les valeurs, -1 une forte corrélation négative, et 0 aucune corrélation (les variables sont indépendantes).
**Exemple** : Nous pouvons calculer la corrélation entre les poids et les tailles des joueurs de baseball à partir de l'ensemble de données mentionné ci-dessus :
```python
print(np.corrcoef(weights,heights))
```
En résultat, nous obtenons une **matrice de corrélation** comme celle-ci :
```
array([[1. , 0.52959196],
[0.52959196, 1. ]])
```
> La matrice de corrélation C peut être calculée pour n'importe quel nombre de séries d'entrée S1, ..., Sn. La valeur de Cij est la corrélation entre Si et Sj, et les éléments diagonaux sont toujours égaux à 1 (ce qui correspond également à l'auto-corrélation de Si).
Dans notre cas, la valeur 0,53 indique qu'il existe une certaine corrélation entre le poids et la taille d'une personne. Nous pouvons également tracer un nuage de points d'une valeur par rapport à l'autre pour voir visuellement la relation :

> Plus d'exemples de corrélation et de covariance peuvent être trouvés dans le [notebook associé](notebook.ipynb).
## Conclusion
Dans cette section, nous avons appris :
* les propriétés statistiques de base des données, telles que la moyenne, la variance, le mode et les quartiles
* les différentes distributions de variables aléatoires, y compris la distribution normale
* comment trouver la corrélation entre différentes propriétés
* comment utiliser des outils mathématiques et statistiques pour prouver certaines hypothèses
* comment calculer des intervalles de confiance pour une variable aléatoire à partir d'un échantillon de données
Bien que cette liste ne soit pas exhaustive des sujets existant dans les probabilités et les statistiques, elle devrait suffire à vous donner un bon départ dans ce cours.
## 🚀 Défi
Utilisez le code d'exemple dans le notebook pour tester d'autres hypothèses :
1. Les premiers buts sont plus âgés que les deuxièmes buts.
2. Les premiers buts sont plus grands que les troisièmes buts.
3. Les arrêts-courts sont plus grands que les deuxièmes buts.
## [Quiz post-cours](https://ff-quizzes.netlify.app/fr/ds/quiz/7)
## Révision et auto-apprentissage
Les probabilités et les statistiques sont un sujet si vaste qu'il mérite son propre cours. Si vous souhaitez approfondir la théorie, vous pouvez continuer à lire certains des livres suivants :
1. [Carlos Fernandez-Granda](https://cims.nyu.edu/~cfgranda/) de l'Université de New York propose d'excellentes notes de cours [Probability and Statistics for Data Science](https://cims.nyu.edu/~cfgranda/pages/stuff/probability_stats_for_DS.pdf) (disponibles en ligne).
1. [Peter et Andrew Bruce. Practical Statistics for Data Scientists.](https://www.oreilly.com/library/view/practical-statistics-for/9781491952955/) [[code d'exemple en R](https://github.com/andrewgbruce/statistics-for-data-scientists)].
1. [James D. Miller. Statistics for Data Science](https://www.packtpub.com/product/statistics-for-data-science/9781788290678) [[code d'exemple en R](https://github.com/PacktPublishing/Statistics-for-Data-Science)].
## Devoir
[Petite étude sur le diabète](assignment.md)
## Crédits
Cette leçon a été rédigée avec ♥️ par [Dmitry Soshnikov](http://soshnikov.com)
---
**Avertissement** :
Ce document a été traduit à l'aide du service de traduction automatique [Co-op Translator](https://github.com/Azure/co-op-translator). Bien que nous nous efforcions d'assurer l'exactitude, veuillez noter que les traductions automatisées peuvent contenir des erreurs ou des inexactitudes. Le document original dans sa langue d'origine doit être considéré comme la source faisant autorité. Pour des informations critiques, il est recommandé de faire appel à une traduction humaine professionnelle. Nous déclinons toute responsabilité en cas de malentendus ou d'interprétations erronées résultant de l'utilisation de cette traduction. Ici, nous calculons également l'**étendue interquartile** IQR=Q3-Q1, et les **valeurs aberrantes** - des valeurs qui se situent en dehors des limites [Q1-1.5*IQR,Q3+1.5*IQR].
Pour une distribution finie contenant un petit nombre de valeurs possibles, une bonne valeur "typique" est celle qui apparaît le plus fréquemment, appelée **mode**. Elle est souvent appliquée aux données catégoriques, comme les couleurs. Prenons une situation où nous avons deux groupes de personnes - certains qui préfèrent fortement le rouge, et d'autres qui préfèrent le bleu. Si nous codons les couleurs par des nombres, la valeur moyenne pour une couleur préférée serait quelque part dans le spectre orange-vert, ce qui n'indique pas la préférence réelle d'aucun groupe. Cependant, le mode serait soit l'une des couleurs, soit les deux couleurs, si le nombre de personnes votant pour elles est égal (dans ce cas, nous appelons l'échantillon **multimodal**).
## Données du monde réel
Lorsque nous analysons des données provenant de la vie réelle, elles ne sont souvent pas des variables aléatoires en tant que telles, dans le sens où nous ne réalisons pas d'expériences avec un résultat inconnu. Par exemple, considérons une équipe de joueurs de baseball et leurs données corporelles, telles que la taille, le poids et l'âge. Ces nombres ne sont pas exactement aléatoires, mais nous pouvons tout de même appliquer les mêmes concepts mathématiques. Par exemple, une séquence de poids de personnes peut être considérée comme une séquence de valeurs tirées d'une variable aléatoire. Voici la séquence des poids de joueurs de baseball réels de la [Major League Baseball](http://mlb.mlb.com/index.jsp), tirée de [ce jeu de données](http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_MLB_HeightsWeights) (pour votre commodité, seuls les 20 premiers poids sont affichés) :
```
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
```
> **Note** : Pour voir un exemple de travail avec ce jeu de données, consultez le [notebook associé](notebook.ipynb). Il y a également un certain nombre de défis tout au long de cette leçon, et vous pouvez les compléter en ajoutant du code à ce notebook. Si vous ne savez pas comment manipuler des données, ne vous inquiétez pas - nous reviendrons sur le travail avec des données en utilisant Python plus tard. Si vous ne savez pas comment exécuter du code dans Jupyter Notebook, consultez [cet article](https://soshnikov.com/education/how-to-execute-notebooks-from-github/).
Voici le diagramme en boîte montrant la moyenne, la médiane et les quartiles pour nos données :

Étant donné que nos données contiennent des informations sur différents **rôles** de joueurs, nous pouvons également réaliser un diagramme en boîte par rôle - cela nous permettra de comprendre comment les valeurs des paramètres diffèrent selon les rôles. Cette fois, nous considérerons la taille :

Ce diagramme suggère qu'en moyenne, la taille des joueurs de première base est supérieure à celle des joueurs de deuxième base. Plus tard dans cette leçon, nous apprendrons comment tester cette hypothèse de manière plus formelle et comment démontrer que nos données sont statistiquement significatives pour le prouver.
> Lorsque nous travaillons avec des données du monde réel, nous supposons que tous les points de données sont des échantillons tirés d'une certaine distribution de probabilité. Cette hypothèse nous permet d'appliquer des techniques d'apprentissage automatique et de construire des modèles prédictifs fonctionnels.
Pour voir quelle est la distribution de nos données, nous pouvons tracer un graphique appelé **histogramme**. L'axe X contiendra un certain nombre d'intervalles de poids différents (appelés **bins**), et l'axe vertical montrera le nombre de fois où notre échantillon de variable aléatoire se trouvait dans un intervalle donné.

À partir de cet histogramme, vous pouvez voir que toutes les valeurs sont centrées autour d'un certain poids moyen, et plus nous nous éloignons de ce poids, moins nous rencontrons de poids de cette valeur. Autrement dit, il est très improbable que le poids d'un joueur de baseball soit très différent du poids moyen. La variance des poids montre dans quelle mesure les poids sont susceptibles de différer de la moyenne.
> Si nous prenons les poids d'autres personnes, pas de la ligue de baseball, la distribution sera probablement différente. Cependant, la forme de la distribution sera la même, mais la moyenne et la variance changeront. Ainsi, si nous entraînons notre modèle sur des joueurs de baseball, il est probable qu'il donne des résultats erronés lorsqu'il est appliqué à des étudiants d'une université, car la distribution sous-jacente est différente.
## Distribution normale
La distribution des poids que nous avons vue ci-dessus est très typique, et de nombreuses mesures du monde réel suivent le même type de distribution, mais avec des moyennes et des variances différentes. Cette distribution est appelée **distribution normale**, et elle joue un rôle très important en statistiques.
Utiliser la distribution normale est une manière correcte de générer des poids aléatoires de joueurs de baseball potentiels. Une fois que nous connaissons le poids moyen `mean` et l'écart-type `std`, nous pouvons générer 1000 échantillons de poids de la manière suivante :
```python
samples = np.random.normal(mean,std,1000)
```
Si nous traçons l'histogramme des échantillons générés, nous verrons une image très similaire à celle montrée ci-dessus. Et si nous augmentons le nombre d'échantillons et le nombre de bins, nous pouvons générer une image de distribution normale plus proche de l'idéal :

*Distribution normale avec moyenne=0 et écart-type=1*
## Intervalles de confiance
Lorsque nous parlons des poids des joueurs de baseball, nous supposons qu'il existe une certaine **variable aléatoire W** qui correspond à la distribution de probabilité idéale des poids de tous les joueurs de baseball (appelée **population**). Notre séquence de poids correspond à un sous-ensemble de tous les joueurs de baseball que nous appelons **échantillon**. Une question intéressante est : pouvons-nous connaître les paramètres de la distribution de W, c'est-à-dire la moyenne et la variance de la population ?
La réponse la plus simple serait de calculer la moyenne et la variance de notre échantillon. Cependant, il pourrait arriver que notre échantillon aléatoire ne représente pas précisément la population complète. Ainsi, il est logique de parler d'**intervalle de confiance**.
> **Intervalle de confiance** est l'estimation de la vraie moyenne de la population donnée notre échantillon, qui est précise avec une certaine probabilité (ou **niveau de confiance**).
Supposons que nous ayons un échantillon X
1, ..., Xn de notre distribution. Chaque fois que nous tirons un échantillon de notre distribution, nous obtenons une valeur moyenne μ différente. Ainsi, μ peut être considéré comme une variable aléatoire. Un **intervalle de confiance** avec une confiance p est une paire de valeurs (Lp,Rp), telle que **P**(Lp≤μ≤Rp) = p, c'est-à-dire qu'il y a une probabilité p que la valeur moyenne mesurée se situe dans l'intervalle.
Il dépasse le cadre de cette introduction de discuter en détail de la manière dont ces intervalles de confiance sont calculés. Vous pouvez trouver plus de détails [sur Wikipédia](https://fr.wikipedia.org/wiki/Intervalle_de_confiance). En résumé, nous définissons la distribution de la moyenne d'échantillon calculée par rapport à la vraie moyenne de la population, appelée **distribution de Student**.
> **Fait intéressant** : La distribution de Student porte le nom du mathématicien William Sealy Gosset, qui a publié son article sous le pseudonyme "Student". Il travaillait dans la brasserie Guinness et, selon une version, son employeur ne voulait pas que le grand public sache qu'ils utilisaient des tests statistiques pour évaluer la qualité des matières premières.
Si nous voulons estimer la moyenne μ de notre population avec une confiance p, nous devons prendre le *(1-p)/2-ème percentile* d'une distribution de Student A, qui peut être obtenu à partir de tables ou calculé à l'aide de fonctions intégrées dans des logiciels statistiques (par exemple Python, R, etc.). L'intervalle pour μ serait alors donné par X±A*D/√n, où X est la moyenne obtenue de l'échantillon, et D est l'écart-type.
> **Note** : Nous omettons également la discussion d'un concept important, celui des [degrés de liberté](https://fr.wikipedia.org/wiki/Degr%C3%A9s_de_libert%C3%A9_(statistiques)), qui est essentiel en relation avec la distribution de Student. Vous pouvez consulter des ouvrages plus complets sur les statistiques pour approfondir ce concept.
Un exemple de calcul d'intervalle de confiance pour les poids et les tailles est donné dans les [notebooks associés](notebook.ipynb).
| p | Moyenne du poids |
|------|------------------|
| 0.85 | 201,73±0,94 |
| 0.90 | 201,73±1,08 |
| 0.95 | 201,73±1,28 |
Remarquez que plus la probabilité de confiance est élevée, plus l'intervalle de confiance est large.
## Test d'hypothèses
Dans notre ensemble de données sur les joueurs de baseball, il existe différents rôles de joueurs, qui peuvent être résumés ci-dessous (consultez le [notebook associé](notebook.ipynb) pour voir comment ce tableau peut être calculé) :
| Rôle | Taille | Poids | Nombre |
|--------------------|----------|----------|--------|
| Receveur | 72,723684 | 204,328947 | 76 |
| Frappeur désigné | 74,222222 | 220,888889 | 18 |
| Premier but | 74,000000 | 213,109091 | 55 |
| Voltigeur | 73,010309 | 199,113402 | 194 |
| Lanceur de relève | 74,374603 | 203,517460 | 315 |
| Deuxième but | 71,362069 | 184,344828 | 58 |
| Arrêt-court | 71,903846 | 182,923077 | 52 |
| Lanceur partant | 74,719457 | 205,163636 | 221 |
| Troisième but | 73,044444 | 200,955556 | 45 |
Nous pouvons remarquer que la taille moyenne des premiers buts est supérieure à celle des deuxièmes buts. Ainsi, nous pourrions être tentés de conclure que **les premiers buts sont plus grands que les deuxièmes buts**.
> Cette affirmation est appelée **une hypothèse**, car nous ne savons pas si ce fait est réellement vrai ou non.
Cependant, il n'est pas toujours évident de pouvoir tirer cette conclusion. D'après la discussion précédente, nous savons que chaque moyenne est associée à un intervalle de confiance, et cette différence peut donc simplement être une erreur statistique. Nous avons besoin d'une méthode plus formelle pour tester notre hypothèse.
Calculons les intervalles de confiance séparément pour les tailles des premiers et deuxièmes buts :
| Confiance | Premiers buts | Deuxièmes buts |
|-----------|---------------|----------------|
| 0.85 | 73,62..74,38 | 71,04..71,69 |
| 0.90 | 73,56..74,44 | 70,99..71,73 |
| 0.95 | 73,47..74,53 | 70,92..71,81 |
Nous pouvons voir qu'à aucun niveau de confiance les intervalles ne se chevauchent. Cela prouve notre hypothèse selon laquelle les premiers buts sont plus grands que les deuxièmes buts.
Plus formellement, le problème que nous résolvons est de voir si **deux distributions de probabilité sont identiques**, ou du moins ont les mêmes paramètres. Selon la distribution, nous devons utiliser différents tests pour cela. Si nous savons que nos distributions sont normales, nous pouvons appliquer le **[test t de Student](https://fr.wikipedia.org/wiki/Test_t_de_Student)**.
Dans le test t de Student, nous calculons ce qu'on appelle la **valeur t**, qui indique la différence entre les moyennes en tenant compte de la variance. Il est démontré que la valeur t suit une **distribution de Student**, ce qui nous permet d'obtenir la valeur seuil pour un niveau de confiance donné **p** (cela peut être calculé ou consulté dans des tables numériques). Nous comparons ensuite la valeur t à ce seuil pour approuver ou rejeter l'hypothèse.
En Python, nous pouvons utiliser le package **SciPy**, qui inclut la fonction `ttest_ind` (en plus de nombreuses autres fonctions statistiques utiles !). Cette fonction calcule la valeur t pour nous et effectue également la recherche inverse de la valeur de confiance p, de sorte que nous pouvons simplement examiner la confiance pour tirer une conclusion.
Par exemple, notre comparaison entre les tailles des premiers et deuxièmes buts nous donne les résultats suivants :
```python
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
```
```
T-value = 7.65
P-value: 9.137321189738925e-12
```
Dans notre cas, la valeur p est très faible, ce qui signifie qu'il existe des preuves solides soutenant que les premiers buts sont plus grands.
Il existe également d'autres types d'hypothèses que nous pourrions vouloir tester, par exemple :
* Prouver qu'un échantillon donné suit une distribution spécifique. Dans notre cas, nous avons supposé que les tailles sont distribuées normalement, mais cela nécessite une vérification statistique formelle.
* Prouver qu'une valeur moyenne d'un échantillon correspond à une valeur prédéfinie.
* Comparer les moyennes de plusieurs échantillons (par exemple, quelle est la différence des niveaux de bonheur entre différents groupes d'âge).
## Loi des grands nombres et théorème central limite
L'une des raisons pour lesquelles la distribution normale est si importante est le **théorème central limite**. Supposons que nous ayons un grand échantillon de N valeurs indépendantes X1, ..., XN, échantillonnées à partir de n'importe quelle distribution avec une moyenne μ et une variance σ2. Alors, pour un N suffisamment grand (en d'autres termes, lorsque N→∞), la moyenne ΣiXi sera distribuée normalement, avec une moyenne μ et une variance σ2/N.
> Une autre façon d'interpréter le théorème central limite est de dire que, quelle que soit la distribution, lorsque vous calculez la moyenne d'une somme de valeurs de variables aléatoires, vous obtenez une distribution normale.
D'après le théorème central limite, il s'ensuit également que, lorsque N→∞, la probabilité que la moyenne de l'échantillon soit égale à μ devient 1. Cela est connu sous le nom de **loi des grands nombres**.
## Covariance et corrélation
L'une des tâches de la science des données est de trouver des relations entre les données. Nous disons que deux séries **corrèlent** lorsqu'elles présentent un comportement similaire au même moment, c'est-à-dire qu'elles augmentent/diminuent simultanément, ou qu'une série augmente lorsque l'autre diminue, et vice versa. En d'autres termes, il semble y avoir une relation entre les deux séries.
> La corrélation n'indique pas nécessairement une relation causale entre deux séries ; parfois, les deux variables peuvent dépendre d'une cause externe, ou il peut s'agir d'une simple coïncidence. Cependant, une forte corrélation mathématique est une bonne indication que deux variables sont d'une certaine manière connectées.
Mathématiquement, le concept principal qui montre la relation entre deux variables aléatoires est la **covariance**, qui est calculée comme suit : Cov(X,Y) = **E**\[(X-**E**(X))(Y-**E**(Y))\]. Nous calculons l'écart des deux variables par rapport à leurs valeurs moyennes, puis le produit de ces écarts. Si les deux variables dévient ensemble, le produit sera toujours une valeur positive, ce qui donnera une covariance positive. Si les deux variables dévient de manière désynchronisée (c'est-à-dire qu'une diminue en dessous de la moyenne lorsque l'autre augmente au-dessus de la moyenne), nous obtiendrons toujours des nombres négatifs, ce qui donnera une covariance négative. Si les écarts ne sont pas dépendants, ils s'annuleront approximativement à zéro.
La valeur absolue de la covariance ne nous dit pas grand-chose sur l'ampleur de la corrélation, car elle dépend de la magnitude des valeurs réelles. Pour la normaliser, nous pouvons diviser la covariance par l'écart-type des deux variables, pour obtenir la **corrélation**. L'avantage est que la corrélation est toujours dans la plage de [-1,1], où 1 indique une forte corrélation positive entre les valeurs, -1 une forte corrélation négative, et 0 aucune corrélation (les variables sont indépendantes).
**Exemple** : Nous pouvons calculer la corrélation entre les poids et les tailles des joueurs de baseball à partir de l'ensemble de données mentionné ci-dessus :
```python
print(np.corrcoef(weights,heights))
```
En résultat, nous obtenons une **matrice de corrélation** comme celle-ci :
```
array([[1. , 0.52959196],
[0.52959196, 1. ]])
```
> La matrice de corrélation C peut être calculée pour n'importe quel nombre de séries d'entrée S1, ..., Sn. La valeur de Cij est la corrélation entre Si et Sj, et les éléments diagonaux sont toujours égaux à 1 (ce qui correspond également à l'auto-corrélation de Si).
Dans notre cas, la valeur 0,53 indique qu'il existe une certaine corrélation entre le poids et la taille d'une personne. Nous pouvons également tracer un nuage de points d'une valeur par rapport à l'autre pour voir visuellement la relation :

> Plus d'exemples de corrélation et de covariance peuvent être trouvés dans le [notebook associé](notebook.ipynb).
## Conclusion
Dans cette section, nous avons appris :
* les propriétés statistiques de base des données, telles que la moyenne, la variance, le mode et les quartiles
* les différentes distributions de variables aléatoires, y compris la distribution normale
* comment trouver la corrélation entre différentes propriétés
* comment utiliser des outils mathématiques et statistiques pour prouver certaines hypothèses
* comment calculer des intervalles de confiance pour une variable aléatoire à partir d'un échantillon de données
Bien que cette liste ne soit pas exhaustive des sujets existant dans les probabilités et les statistiques, elle devrait suffire à vous donner un bon départ dans ce cours.
## 🚀 Défi
Utilisez le code d'exemple dans le notebook pour tester d'autres hypothèses :
1. Les premiers buts sont plus âgés que les deuxièmes buts.
2. Les premiers buts sont plus grands que les troisièmes buts.
3. Les arrêts-courts sont plus grands que les deuxièmes buts.
## [Quiz post-cours](https://ff-quizzes.netlify.app/fr/ds/quiz/7)
## Révision et auto-apprentissage
Les probabilités et les statistiques sont un sujet si vaste qu'il mérite son propre cours. Si vous souhaitez approfondir la théorie, vous pouvez continuer à lire certains des livres suivants :
1. [Carlos Fernandez-Granda](https://cims.nyu.edu/~cfgranda/) de l'Université de New York propose d'excellentes notes de cours [Probability and Statistics for Data Science](https://cims.nyu.edu/~cfgranda/pages/stuff/probability_stats_for_DS.pdf) (disponibles en ligne).
1. [Peter et Andrew Bruce. Practical Statistics for Data Scientists.](https://www.oreilly.com/library/view/practical-statistics-for/9781491952955/) [[code d'exemple en R](https://github.com/andrewgbruce/statistics-for-data-scientists)].
1. [James D. Miller. Statistics for Data Science](https://www.packtpub.com/product/statistics-for-data-science/9781788290678) [[code d'exemple en R](https://github.com/PacktPublishing/Statistics-for-Data-Science)].
## Devoir
[Petite étude sur le diabète](assignment.md)
## Crédits
Cette leçon a été rédigée avec ♥️ par [Dmitry Soshnikov](http://soshnikov.com)
---
**Avertissement** :
Ce document a été traduit à l'aide du service de traduction automatique [Co-op Translator](https://github.com/Azure/co-op-translator). Bien que nous nous efforcions d'assurer l'exactitude, veuillez noter que les traductions automatisées peuvent contenir des erreurs ou des inexactitudes. Le document original dans sa langue d'origine doit être considéré comme la source faisant autorité. Pour des informations critiques, il est recommandé de faire appel à une traduction humaine professionnelle. Nous déclinons toute responsabilité en cas de malentendus ou d'interprétations erronées résultant de l'utilisation de cette traduction.
Ici, nous calculons également l'**étendue interquartile** IQR=Q3-Q1, et les **valeurs aberrantes** - des valeurs qui se situent en dehors des limites [Q1-1.5*IQR,Q3+1.5*IQR].
Pour une distribution finie contenant un petit nombre de valeurs possibles, une bonne valeur "typique" est celle qui apparaît le plus fréquemment, appelée **mode**. Elle est souvent appliquée aux données catégoriques, comme les couleurs. Prenons une situation où nous avons deux groupes de personnes - certains qui préfèrent fortement le rouge, et d'autres qui préfèrent le bleu. Si nous codons les couleurs par des nombres, la valeur moyenne pour une couleur préférée serait quelque part dans le spectre orange-vert, ce qui n'indique pas la préférence réelle d'aucun groupe. Cependant, le mode serait soit l'une des couleurs, soit les deux couleurs, si le nombre de personnes votant pour elles est égal (dans ce cas, nous appelons l'échantillon **multimodal**).
## Données du monde réel
Lorsque nous analysons des données provenant de la vie réelle, elles ne sont souvent pas des variables aléatoires en tant que telles, dans le sens où nous ne réalisons pas d'expériences avec un résultat inconnu. Par exemple, considérons une équipe de joueurs de baseball et leurs données corporelles, telles que la taille, le poids et l'âge. Ces nombres ne sont pas exactement aléatoires, mais nous pouvons tout de même appliquer les mêmes concepts mathématiques. Par exemple, une séquence de poids de personnes peut être considérée comme une séquence de valeurs tirées d'une variable aléatoire. Voici la séquence des poids de joueurs de baseball réels de la [Major League Baseball](http://mlb.mlb.com/index.jsp), tirée de [ce jeu de données](http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_MLB_HeightsWeights) (pour votre commodité, seuls les 20 premiers poids sont affichés) :
```
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
```
> **Note** : Pour voir un exemple de travail avec ce jeu de données, consultez le [notebook associé](notebook.ipynb). Il y a également un certain nombre de défis tout au long de cette leçon, et vous pouvez les compléter en ajoutant du code à ce notebook. Si vous ne savez pas comment manipuler des données, ne vous inquiétez pas - nous reviendrons sur le travail avec des données en utilisant Python plus tard. Si vous ne savez pas comment exécuter du code dans Jupyter Notebook, consultez [cet article](https://soshnikov.com/education/how-to-execute-notebooks-from-github/).
Voici le diagramme en boîte montrant la moyenne, la médiane et les quartiles pour nos données :

Étant donné que nos données contiennent des informations sur différents **rôles** de joueurs, nous pouvons également réaliser un diagramme en boîte par rôle - cela nous permettra de comprendre comment les valeurs des paramètres diffèrent selon les rôles. Cette fois, nous considérerons la taille :

Ce diagramme suggère qu'en moyenne, la taille des joueurs de première base est supérieure à celle des joueurs de deuxième base. Plus tard dans cette leçon, nous apprendrons comment tester cette hypothèse de manière plus formelle et comment démontrer que nos données sont statistiquement significatives pour le prouver.
> Lorsque nous travaillons avec des données du monde réel, nous supposons que tous les points de données sont des échantillons tirés d'une certaine distribution de probabilité. Cette hypothèse nous permet d'appliquer des techniques d'apprentissage automatique et de construire des modèles prédictifs fonctionnels.
Pour voir quelle est la distribution de nos données, nous pouvons tracer un graphique appelé **histogramme**. L'axe X contiendra un certain nombre d'intervalles de poids différents (appelés **bins**), et l'axe vertical montrera le nombre de fois où notre échantillon de variable aléatoire se trouvait dans un intervalle donné.

À partir de cet histogramme, vous pouvez voir que toutes les valeurs sont centrées autour d'un certain poids moyen, et plus nous nous éloignons de ce poids, moins nous rencontrons de poids de cette valeur. Autrement dit, il est très improbable que le poids d'un joueur de baseball soit très différent du poids moyen. La variance des poids montre dans quelle mesure les poids sont susceptibles de différer de la moyenne.
> Si nous prenons les poids d'autres personnes, pas de la ligue de baseball, la distribution sera probablement différente. Cependant, la forme de la distribution sera la même, mais la moyenne et la variance changeront. Ainsi, si nous entraînons notre modèle sur des joueurs de baseball, il est probable qu'il donne des résultats erronés lorsqu'il est appliqué à des étudiants d'une université, car la distribution sous-jacente est différente.
## Distribution normale
La distribution des poids que nous avons vue ci-dessus est très typique, et de nombreuses mesures du monde réel suivent le même type de distribution, mais avec des moyennes et des variances différentes. Cette distribution est appelée **distribution normale**, et elle joue un rôle très important en statistiques.
Utiliser la distribution normale est une manière correcte de générer des poids aléatoires de joueurs de baseball potentiels. Une fois que nous connaissons le poids moyen `mean` et l'écart-type `std`, nous pouvons générer 1000 échantillons de poids de la manière suivante :
```python
samples = np.random.normal(mean,std,1000)
```
Si nous traçons l'histogramme des échantillons générés, nous verrons une image très similaire à celle montrée ci-dessus. Et si nous augmentons le nombre d'échantillons et le nombre de bins, nous pouvons générer une image de distribution normale plus proche de l'idéal :

*Distribution normale avec moyenne=0 et écart-type=1*
## Intervalles de confiance
Lorsque nous parlons des poids des joueurs de baseball, nous supposons qu'il existe une certaine **variable aléatoire W** qui correspond à la distribution de probabilité idéale des poids de tous les joueurs de baseball (appelée **population**). Notre séquence de poids correspond à un sous-ensemble de tous les joueurs de baseball que nous appelons **échantillon**. Une question intéressante est : pouvons-nous connaître les paramètres de la distribution de W, c'est-à-dire la moyenne et la variance de la population ?
La réponse la plus simple serait de calculer la moyenne et la variance de notre échantillon. Cependant, il pourrait arriver que notre échantillon aléatoire ne représente pas précisément la population complète. Ainsi, il est logique de parler d'**intervalle de confiance**.
> **Intervalle de confiance** est l'estimation de la vraie moyenne de la population donnée notre échantillon, qui est précise avec une certaine probabilité (ou **niveau de confiance**).
Supposons que nous ayons un échantillon X
1, ..., Xn de notre distribution. Chaque fois que nous tirons un échantillon de notre distribution, nous obtenons une valeur moyenne μ différente. Ainsi, μ peut être considéré comme une variable aléatoire. Un **intervalle de confiance** avec une confiance p est une paire de valeurs (Lp,Rp), telle que **P**(Lp≤μ≤Rp) = p, c'est-à-dire qu'il y a une probabilité p que la valeur moyenne mesurée se situe dans l'intervalle.
Il dépasse le cadre de cette introduction de discuter en détail de la manière dont ces intervalles de confiance sont calculés. Vous pouvez trouver plus de détails [sur Wikipédia](https://fr.wikipedia.org/wiki/Intervalle_de_confiance). En résumé, nous définissons la distribution de la moyenne d'échantillon calculée par rapport à la vraie moyenne de la population, appelée **distribution de Student**.
> **Fait intéressant** : La distribution de Student porte le nom du mathématicien William Sealy Gosset, qui a publié son article sous le pseudonyme "Student". Il travaillait dans la brasserie Guinness et, selon une version, son employeur ne voulait pas que le grand public sache qu'ils utilisaient des tests statistiques pour évaluer la qualité des matières premières.
Si nous voulons estimer la moyenne μ de notre population avec une confiance p, nous devons prendre le *(1-p)/2-ème percentile* d'une distribution de Student A, qui peut être obtenu à partir de tables ou calculé à l'aide de fonctions intégrées dans des logiciels statistiques (par exemple Python, R, etc.). L'intervalle pour μ serait alors donné par X±A*D/√n, où X est la moyenne obtenue de l'échantillon, et D est l'écart-type.
> **Note** : Nous omettons également la discussion d'un concept important, celui des [degrés de liberté](https://fr.wikipedia.org/wiki/Degr%C3%A9s_de_libert%C3%A9_(statistiques)), qui est essentiel en relation avec la distribution de Student. Vous pouvez consulter des ouvrages plus complets sur les statistiques pour approfondir ce concept.
Un exemple de calcul d'intervalle de confiance pour les poids et les tailles est donné dans les [notebooks associés](notebook.ipynb).
| p | Moyenne du poids |
|------|------------------|
| 0.85 | 201,73±0,94 |
| 0.90 | 201,73±1,08 |
| 0.95 | 201,73±1,28 |
Remarquez que plus la probabilité de confiance est élevée, plus l'intervalle de confiance est large.
## Test d'hypothèses
Dans notre ensemble de données sur les joueurs de baseball, il existe différents rôles de joueurs, qui peuvent être résumés ci-dessous (consultez le [notebook associé](notebook.ipynb) pour voir comment ce tableau peut être calculé) :
| Rôle | Taille | Poids | Nombre |
|--------------------|----------|----------|--------|
| Receveur | 72,723684 | 204,328947 | 76 |
| Frappeur désigné | 74,222222 | 220,888889 | 18 |
| Premier but | 74,000000 | 213,109091 | 55 |
| Voltigeur | 73,010309 | 199,113402 | 194 |
| Lanceur de relève | 74,374603 | 203,517460 | 315 |
| Deuxième but | 71,362069 | 184,344828 | 58 |
| Arrêt-court | 71,903846 | 182,923077 | 52 |
| Lanceur partant | 74,719457 | 205,163636 | 221 |
| Troisième but | 73,044444 | 200,955556 | 45 |
Nous pouvons remarquer que la taille moyenne des premiers buts est supérieure à celle des deuxièmes buts. Ainsi, nous pourrions être tentés de conclure que **les premiers buts sont plus grands que les deuxièmes buts**.
> Cette affirmation est appelée **une hypothèse**, car nous ne savons pas si ce fait est réellement vrai ou non.
Cependant, il n'est pas toujours évident de pouvoir tirer cette conclusion. D'après la discussion précédente, nous savons que chaque moyenne est associée à un intervalle de confiance, et cette différence peut donc simplement être une erreur statistique. Nous avons besoin d'une méthode plus formelle pour tester notre hypothèse.
Calculons les intervalles de confiance séparément pour les tailles des premiers et deuxièmes buts :
| Confiance | Premiers buts | Deuxièmes buts |
|-----------|---------------|----------------|
| 0.85 | 73,62..74,38 | 71,04..71,69 |
| 0.90 | 73,56..74,44 | 70,99..71,73 |
| 0.95 | 73,47..74,53 | 70,92..71,81 |
Nous pouvons voir qu'à aucun niveau de confiance les intervalles ne se chevauchent. Cela prouve notre hypothèse selon laquelle les premiers buts sont plus grands que les deuxièmes buts.
Plus formellement, le problème que nous résolvons est de voir si **deux distributions de probabilité sont identiques**, ou du moins ont les mêmes paramètres. Selon la distribution, nous devons utiliser différents tests pour cela. Si nous savons que nos distributions sont normales, nous pouvons appliquer le **[test t de Student](https://fr.wikipedia.org/wiki/Test_t_de_Student)**.
Dans le test t de Student, nous calculons ce qu'on appelle la **valeur t**, qui indique la différence entre les moyennes en tenant compte de la variance. Il est démontré que la valeur t suit une **distribution de Student**, ce qui nous permet d'obtenir la valeur seuil pour un niveau de confiance donné **p** (cela peut être calculé ou consulté dans des tables numériques). Nous comparons ensuite la valeur t à ce seuil pour approuver ou rejeter l'hypothèse.
En Python, nous pouvons utiliser le package **SciPy**, qui inclut la fonction `ttest_ind` (en plus de nombreuses autres fonctions statistiques utiles !). Cette fonction calcule la valeur t pour nous et effectue également la recherche inverse de la valeur de confiance p, de sorte que nous pouvons simplement examiner la confiance pour tirer une conclusion.
Par exemple, notre comparaison entre les tailles des premiers et deuxièmes buts nous donne les résultats suivants :
```python
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
```
```
T-value = 7.65
P-value: 9.137321189738925e-12
```
Dans notre cas, la valeur p est très faible, ce qui signifie qu'il existe des preuves solides soutenant que les premiers buts sont plus grands.
Il existe également d'autres types d'hypothèses que nous pourrions vouloir tester, par exemple :
* Prouver qu'un échantillon donné suit une distribution spécifique. Dans notre cas, nous avons supposé que les tailles sont distribuées normalement, mais cela nécessite une vérification statistique formelle.
* Prouver qu'une valeur moyenne d'un échantillon correspond à une valeur prédéfinie.
* Comparer les moyennes de plusieurs échantillons (par exemple, quelle est la différence des niveaux de bonheur entre différents groupes d'âge).
## Loi des grands nombres et théorème central limite
L'une des raisons pour lesquelles la distribution normale est si importante est le **théorème central limite**. Supposons que nous ayons un grand échantillon de N valeurs indépendantes X1, ..., XN, échantillonnées à partir de n'importe quelle distribution avec une moyenne μ et une variance σ2. Alors, pour un N suffisamment grand (en d'autres termes, lorsque N→∞), la moyenne ΣiXi sera distribuée normalement, avec une moyenne μ et une variance σ2/N.
> Une autre façon d'interpréter le théorème central limite est de dire que, quelle que soit la distribution, lorsque vous calculez la moyenne d'une somme de valeurs de variables aléatoires, vous obtenez une distribution normale.
D'après le théorème central limite, il s'ensuit également que, lorsque N→∞, la probabilité que la moyenne de l'échantillon soit égale à μ devient 1. Cela est connu sous le nom de **loi des grands nombres**.
## Covariance et corrélation
L'une des tâches de la science des données est de trouver des relations entre les données. Nous disons que deux séries **corrèlent** lorsqu'elles présentent un comportement similaire au même moment, c'est-à-dire qu'elles augmentent/diminuent simultanément, ou qu'une série augmente lorsque l'autre diminue, et vice versa. En d'autres termes, il semble y avoir une relation entre les deux séries.
> La corrélation n'indique pas nécessairement une relation causale entre deux séries ; parfois, les deux variables peuvent dépendre d'une cause externe, ou il peut s'agir d'une simple coïncidence. Cependant, une forte corrélation mathématique est une bonne indication que deux variables sont d'une certaine manière connectées.
Mathématiquement, le concept principal qui montre la relation entre deux variables aléatoires est la **covariance**, qui est calculée comme suit : Cov(X,Y) = **E**\[(X-**E**(X))(Y-**E**(Y))\]. Nous calculons l'écart des deux variables par rapport à leurs valeurs moyennes, puis le produit de ces écarts. Si les deux variables dévient ensemble, le produit sera toujours une valeur positive, ce qui donnera une covariance positive. Si les deux variables dévient de manière désynchronisée (c'est-à-dire qu'une diminue en dessous de la moyenne lorsque l'autre augmente au-dessus de la moyenne), nous obtiendrons toujours des nombres négatifs, ce qui donnera une covariance négative. Si les écarts ne sont pas dépendants, ils s'annuleront approximativement à zéro.
La valeur absolue de la covariance ne nous dit pas grand-chose sur l'ampleur de la corrélation, car elle dépend de la magnitude des valeurs réelles. Pour la normaliser, nous pouvons diviser la covariance par l'écart-type des deux variables, pour obtenir la **corrélation**. L'avantage est que la corrélation est toujours dans la plage de [-1,1], où 1 indique une forte corrélation positive entre les valeurs, -1 une forte corrélation négative, et 0 aucune corrélation (les variables sont indépendantes).
**Exemple** : Nous pouvons calculer la corrélation entre les poids et les tailles des joueurs de baseball à partir de l'ensemble de données mentionné ci-dessus :
```python
print(np.corrcoef(weights,heights))
```
En résultat, nous obtenons une **matrice de corrélation** comme celle-ci :
```
array([[1. , 0.52959196],
[0.52959196, 1. ]])
```
> La matrice de corrélation C peut être calculée pour n'importe quel nombre de séries d'entrée S1, ..., Sn. La valeur de Cij est la corrélation entre Si et Sj, et les éléments diagonaux sont toujours égaux à 1 (ce qui correspond également à l'auto-corrélation de Si).
Dans notre cas, la valeur 0,53 indique qu'il existe une certaine corrélation entre le poids et la taille d'une personne. Nous pouvons également tracer un nuage de points d'une valeur par rapport à l'autre pour voir visuellement la relation :

> Plus d'exemples de corrélation et de covariance peuvent être trouvés dans le [notebook associé](notebook.ipynb).
## Conclusion
Dans cette section, nous avons appris :
* les propriétés statistiques de base des données, telles que la moyenne, la variance, le mode et les quartiles
* les différentes distributions de variables aléatoires, y compris la distribution normale
* comment trouver la corrélation entre différentes propriétés
* comment utiliser des outils mathématiques et statistiques pour prouver certaines hypothèses
* comment calculer des intervalles de confiance pour une variable aléatoire à partir d'un échantillon de données
Bien que cette liste ne soit pas exhaustive des sujets existant dans les probabilités et les statistiques, elle devrait suffire à vous donner un bon départ dans ce cours.
## 🚀 Défi
Utilisez le code d'exemple dans le notebook pour tester d'autres hypothèses :
1. Les premiers buts sont plus âgés que les deuxièmes buts.
2. Les premiers buts sont plus grands que les troisièmes buts.
3. Les arrêts-courts sont plus grands que les deuxièmes buts.
## [Quiz post-cours](https://ff-quizzes.netlify.app/fr/ds/quiz/7)
## Révision et auto-apprentissage
Les probabilités et les statistiques sont un sujet si vaste qu'il mérite son propre cours. Si vous souhaitez approfondir la théorie, vous pouvez continuer à lire certains des livres suivants :
1. [Carlos Fernandez-Granda](https://cims.nyu.edu/~cfgranda/) de l'Université de New York propose d'excellentes notes de cours [Probability and Statistics for Data Science](https://cims.nyu.edu/~cfgranda/pages/stuff/probability_stats_for_DS.pdf) (disponibles en ligne).
1. [Peter et Andrew Bruce. Practical Statistics for Data Scientists.](https://www.oreilly.com/library/view/practical-statistics-for/9781491952955/) [[code d'exemple en R](https://github.com/andrewgbruce/statistics-for-data-scientists)].
1. [James D. Miller. Statistics for Data Science](https://www.packtpub.com/product/statistics-for-data-science/9781788290678) [[code d'exemple en R](https://github.com/PacktPublishing/Statistics-for-Data-Science)].
## Devoir
[Petite étude sur le diabète](assignment.md)
## Crédits
Cette leçon a été rédigée avec ♥️ par [Dmitry Soshnikov](http://soshnikov.com)
---
**Avertissement** :
Ce document a été traduit à l'aide du service de traduction automatique [Co-op Translator](https://github.com/Azure/co-op-translator). Bien que nous nous efforcions d'assurer l'exactitude, veuillez noter que les traductions automatisées peuvent contenir des erreurs ou des inexactitudes. Le document original dans sa langue d'origine doit être considéré comme la source faisant autorité. Pour des informations critiques, il est recommandé de faire appel à une traduction humaine professionnelle. Nous déclinons toute responsabilité en cas de malentendus ou d'interprétations erronées résultant de l'utilisation de cette traduction.