# Eine kurze Einführung in Statistik und Wahrscheinlichkeitsrechnung
| ](../../sketchnotes/04-Statistics-Probability.png)|
|:---:|
| Statistik und Wahrscheinlichkeitsrechnung - _Sketchnote von [@nitya](https://twitter.com/nitya)_ |
Statistik und Wahrscheinlichkeitsrechnung sind zwei eng miteinander verbundene Bereiche der Mathematik, die für Data Science von großer Bedeutung sind. Es ist möglich, mit Daten zu arbeiten, ohne tiefgehende mathematische Kenntnisse zu haben, aber es ist dennoch hilfreich, zumindest einige grundlegende Konzepte zu kennen. Hier geben wir eine kurze Einführung, die Ihnen den Einstieg erleichtert.
[](https://youtu.be/Z5Zy85g4Yjw)
## [Quiz vor der Vorlesung](https://ff-quizzes.netlify.app/en/ds/quiz/6)
## Wahrscheinlichkeit und Zufallsvariablen
**Wahrscheinlichkeit** ist eine Zahl zwischen 0 und 1, die angibt, wie wahrscheinlich ein **Ereignis** ist. Sie wird definiert als die Anzahl der positiven Ergebnisse (die zum Ereignis führen), geteilt durch die Gesamtanzahl der Ergebnisse, vorausgesetzt, dass alle Ergebnisse gleich wahrscheinlich sind. Zum Beispiel: Wenn wir einen Würfel werfen, beträgt die Wahrscheinlichkeit, eine gerade Zahl zu erhalten, 3/6 = 0,5.
Wenn wir über Ereignisse sprechen, verwenden wir **Zufallsvariablen**. Zum Beispiel würde die Zufallsvariable, die die Zahl beim Würfeln darstellt, Werte von 1 bis 6 annehmen. Die Menge der Zahlen von 1 bis 6 wird als **Stichprobenraum** bezeichnet. Wir können über die Wahrscheinlichkeit sprechen, dass eine Zufallsvariable einen bestimmten Wert annimmt, z. B. P(X=3)=1/6.
Die Zufallsvariable im obigen Beispiel wird als **diskret** bezeichnet, da sie einen abzählbaren Stichprobenraum hat, d. h. es gibt separate Werte, die aufgezählt werden können. Es gibt jedoch Fälle, in denen der Stichprobenraum ein Intervall von reellen Zahlen oder die gesamte Menge der reellen Zahlen ist. Solche Variablen werden als **stetig** bezeichnet. Ein gutes Beispiel ist die Ankunftszeit eines Busses.
## Wahrscheinlichkeitsverteilung
Im Fall von diskreten Zufallsvariablen ist es einfach, die Wahrscheinlichkeit jedes Ereignisses durch eine Funktion P(X) zu beschreiben. Für jeden Wert *s* aus dem Stichprobenraum *S* gibt sie eine Zahl zwischen 0 und 1 an, sodass die Summe aller Werte von P(X=s) für alle Ereignisse 1 ergibt.
Die bekannteste diskrete Verteilung ist die **gleichmäßige Verteilung**, bei der es einen Stichprobenraum mit N Elementen gibt, wobei jedes Element die gleiche Wahrscheinlichkeit von 1/N hat.
Es ist schwieriger, die Wahrscheinlichkeitsverteilung einer stetigen Variablen zu beschreiben, deren Werte aus einem Intervall [a,b] oder der gesamten Menge der reellen Zahlen ℝ stammen. Betrachten wir den Fall der Ankunftszeit eines Busses. Tatsächlich ist die Wahrscheinlichkeit, dass ein Bus zu einem exakt bestimmten Zeitpunkt *t* ankommt, gleich 0!
> Jetzt wissen Sie, dass Ereignisse mit einer Wahrscheinlichkeit von 0 passieren – und das sogar sehr oft! Zumindest jedes Mal, wenn der Bus ankommt!
Wir können nur über die Wahrscheinlichkeit sprechen, dass eine Variable in ein bestimmtes Werteintervall fällt, z. B. P(t1≤X2). In diesem Fall wird die Wahrscheinlichkeitsverteilung durch eine **Wahrscheinlichkeitsdichtefunktion** p(x) beschrieben, sodass
 Hier berechnen wir auch den **Interquartilsabstand** IQR=Q3-Q1 und sogenannte **Ausreißer** – Werte, die außerhalb der Grenzen [Q1-1.5*IQR, Q3+1.5*IQR] liegen.
Für eine endliche Verteilung, die nur eine kleine Anzahl möglicher Werte enthält, ist ein guter "typischer" Wert derjenige, der am häufigsten vorkommt, der sogenannte **Modus**. Er wird oft auf kategoriale Daten angewendet, wie z. B. Farben. Betrachten Sie eine Situation, in der wir zwei Gruppen von Menschen haben – einige, die stark Rot bevorzugen, und andere, die Blau bevorzugen. Wenn wir Farben durch Zahlen kodieren, würde der Mittelwert für die Lieblingsfarbe irgendwo im orange-grünen Spektrum liegen, was die tatsächliche Präferenz keiner der Gruppen widerspiegelt. Der Modus hingegen wäre entweder eine der Farben oder beide Farben, wenn die Anzahl der Personen, die für sie stimmen, gleich ist (in diesem Fall nennen wir die Stichprobe **multimodal**).
## Reale Daten
Wenn wir Daten aus der realen Welt analysieren, sind sie oft keine Zufallsvariablen im eigentlichen Sinne, da wir keine Experimente mit unbekanntem Ergebnis durchführen. Betrachten Sie zum Beispiel ein Team von Baseballspielern und deren Körperdaten wie Größe, Gewicht und Alter. Diese Zahlen sind nicht wirklich zufällig, aber wir können dennoch dieselben mathematischen Konzepte anwenden. Zum Beispiel kann eine Sequenz von Gewichten von Personen als eine Sequenz von Werten betrachtet werden, die aus einer Zufallsvariablen gezogen wurden. Unten sehen Sie die Gewichtssequenz tatsächlicher Baseballspieler aus der [Major League Baseball](http://mlb.mlb.com/index.jsp), entnommen aus [diesem Datensatz](http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_MLB_HeightsWeights) (der Übersicht halber sind nur die ersten 20 Werte dargestellt):
```
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
```
> **Hinweis**: Um ein Beispiel für die Arbeit mit diesem Datensatz zu sehen, werfen Sie einen Blick auf das [begleitende Notebook](notebook.ipynb). Es gibt auch eine Reihe von Herausforderungen in dieser Lektion, die Sie durch das Hinzufügen von Code zu diesem Notebook abschließen können. Wenn Sie nicht sicher sind, wie man mit Daten arbeitet, machen Sie sich keine Sorgen – wir werden später darauf zurückkommen, wie man mit Python arbeitet. Wenn Sie nicht wissen, wie man Code in einem Jupyter Notebook ausführt, lesen Sie [diesen Artikel](https://soshnikov.com/education/how-to-execute-notebooks-from-github/).
Hier ist der Boxplot, der Mittelwert, Median und Quartile für unsere Daten zeigt:
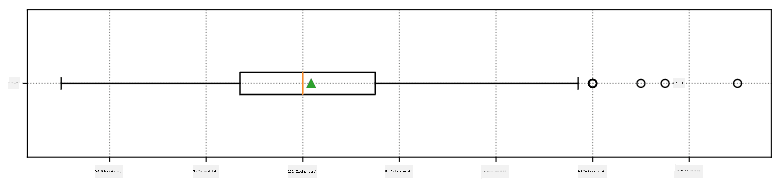
Da unsere Daten Informationen über verschiedene Spieler**rollen** enthalten, können wir auch den Boxplot nach Rollen erstellen – so können wir erkennen, wie sich die Parameterwerte je nach Rolle unterscheiden. Diesmal betrachten wir die Größe:
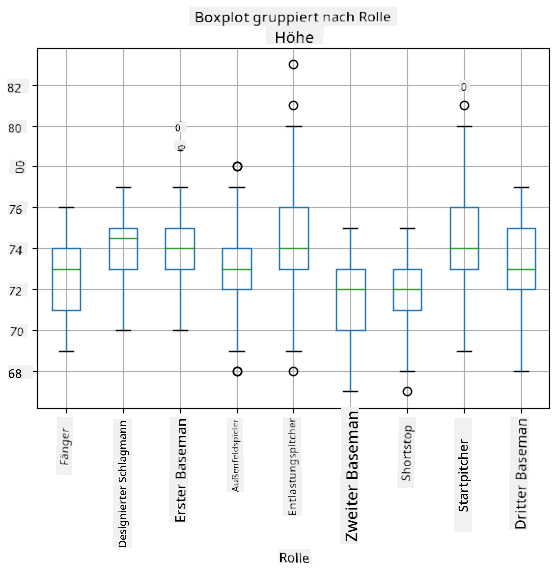
Dieses Diagramm deutet darauf hin, dass die Größe von First Basemen im Durchschnitt höher ist als die von Second Basemen. Später in dieser Lektion werden wir lernen, wie wir diese Hypothese formeller testen können und wie wir zeigen können, dass unsere Daten statistisch signifikant sind, um dies zu belegen.
> Wenn wir mit realen Daten arbeiten, gehen wir davon aus, dass alle Datenpunkte Stichproben sind, die aus einer Wahrscheinlichkeitsverteilung gezogen wurden. Diese Annahme ermöglicht es uns, maschinelles Lernen anzuwenden und funktionierende Vorhersagemodelle zu erstellen.
Um zu sehen, wie die Verteilung unserer Daten aussieht, können wir ein Diagramm namens **Histogramm** erstellen. Die X-Achse enthält eine Anzahl verschiedener Gewichtsintervalle (sogenannte **Bins**), und die Y-Achse zeigt die Anzahl der Male, die unsere Zufallsvariablenstichprobe in ein bestimmtes Intervall fiel.
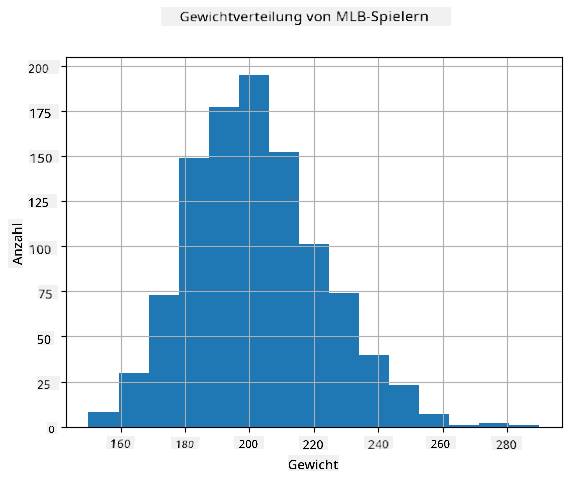
Aus diesem Histogramm können Sie erkennen, dass alle Werte um einen bestimmten mittleren Wert zentriert sind und dass die Wahrscheinlichkeit, dass ein Gewicht stark vom Mittelwert abweicht, geringer ist. Die Varianz der Gewichte zeigt, in welchem Maße die Gewichte wahrscheinlich vom Mittelwert abweichen.
> Wenn wir die Gewichte anderer Personen, die nicht aus der Baseballliga stammen, betrachten, ist die Verteilung wahrscheinlich anders. Die Form der Verteilung bleibt jedoch gleich, aber Mittelwert und Varianz ändern sich. Wenn wir unser Modell auf Baseballspieler trainieren, wird es wahrscheinlich falsche Ergebnisse liefern, wenn es auf Universitätsstudenten angewendet wird, da die zugrunde liegende Verteilung unterschiedlich ist.
## Normalverteilung
Die Verteilung der Gewichte, die wir oben gesehen haben, ist sehr typisch, und viele Messungen aus der realen Welt folgen demselben Verteilungstyp, jedoch mit unterschiedlichem Mittelwert und Varianz. Diese Verteilung wird als **Normalverteilung** bezeichnet und spielt eine sehr wichtige Rolle in der Statistik.
Die Verwendung der Normalverteilung ist eine korrekte Methode, um zufällige Gewichte potenzieller Baseballspieler zu generieren. Sobald wir den mittleren Wert `mean` und die Standardabweichung `std` kennen, können wir 1000 Gewichtsstichproben wie folgt generieren:
```python
samples = np.random.normal(mean,std,1000)
```
Wenn wir das Histogramm der generierten Stichproben zeichnen, sehen wir ein Bild, das dem oben gezeigten sehr ähnlich ist. Und wenn wir die Anzahl der Stichproben und die Anzahl der Bins erhöhen, können wir ein Bild einer Normalverteilung erzeugen, das näher an der idealen Form liegt:
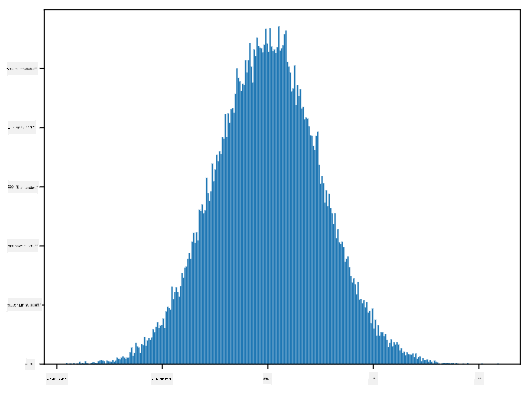
*Normalverteilung mit Mittelwert=0 und Standardabweichung=1*
## Konfidenzintervalle
Wenn wir über die Gewichte von Baseballspielern sprechen, nehmen wir an, dass es eine bestimmte **Zufallsvariable W** gibt, die der idealen Wahrscheinlichkeitsverteilung der Gewichte aller Baseballspieler entspricht (sogenannte **Population**). Unsere Gewichtssequenz entspricht einer Teilmenge aller Baseballspieler, die wir als **Stichprobe** bezeichnen. Eine interessante Frage ist: Können wir die Parameter der Verteilung von W kennen, d. h. den Mittelwert und die Varianz der Population?
Die einfachste Antwort wäre, den Mittelwert und die Varianz unserer Stichprobe zu berechnen. Es könnte jedoch sein, dass unsere zufällige Stichprobe die gesamte Population nicht genau repräsentiert. Daher macht es Sinn, über **Konfidenzintervalle** zu sprechen.
> **Konfidenzintervall** ist die Schätzung des tatsächlichen Mittelwerts der Population basierend auf unserer Stichprobe, die mit einer bestimmten Wahrscheinlichkeit (oder **Konfidenzniveau**) korrekt ist.
Angenommen, wir haben eine Stichprobe X...
1, ..., Xn aus unserer Verteilung. Jedes Mal, wenn wir eine Stichprobe aus unserer Verteilung ziehen, erhalten wir einen anderen Mittelwert μ. Daher kann μ als Zufallsvariable betrachtet werden. Ein **Konfidenzintervall** mit Konfidenz p ist ein Wertepaar (Lp,Rp), sodass **P**(Lp≤μ≤Rp) = p, d.h. die Wahrscheinlichkeit, dass der gemessene Mittelwert innerhalb des Intervalls liegt, entspricht p.
Es geht über unsere kurze Einführung hinaus, im Detail zu erklären, wie diese Konfidenzintervalle berechnet werden. Weitere Details finden Sie [auf Wikipedia](https://en.wikipedia.org/wiki/Confidence_interval). Kurz gesagt, wir definieren die Verteilung des berechneten Stichprobenmittelwerts relativ zum wahren Mittelwert der Population, die als **Student-Verteilung** bezeichnet wird.
> **Interessante Tatsache**: Die Student-Verteilung ist nach dem Mathematiker William Sealy Gosset benannt, der seine Arbeit unter dem Pseudonym "Student" veröffentlichte. Er arbeitete in der Guinness-Brauerei, und laut einer Version wollte sein Arbeitgeber nicht, dass die Öffentlichkeit erfährt, dass sie statistische Tests zur Bestimmung der Qualität der Rohstoffe verwendeten.
Wenn wir den Mittelwert μ unserer Population mit Konfidenz p schätzen möchten, müssen wir das *(1-p)/2-te Perzentil* einer Student-Verteilung A nehmen, das entweder aus Tabellen entnommen oder mithilfe eingebauter Funktionen statistischer Software (z. B. Python, R usw.) berechnet werden kann. Dann wird das Intervall für μ durch X±A*D/√n gegeben, wobei X der erhaltene Mittelwert der Stichprobe und D die Standardabweichung ist.
> **Hinweis**: Wir lassen auch die Diskussion über ein wichtiges Konzept der [Freiheitsgrade](https://en.wikipedia.org/wiki/Degrees_of_freedom_(statistics)) aus, das im Zusammenhang mit der Student-Verteilung wichtig ist. Sie können auf umfassendere Bücher über Statistik zurückgreifen, um dieses Konzept tiefer zu verstehen.
Ein Beispiel für die Berechnung des Konfidenzintervalls für Gewichte und Größen finden Sie in den [begleitenden Notebooks](notebook.ipynb).
| p | Gewichtsmittelwert |
|-----|------------------|
| 0.85 | 201.73±0.94 |
| 0.90 | 201.73±1.08 |
| 0.95 | 201.73±1.28 |
Beachten Sie, dass je höher die Konfidenzwahrscheinlichkeit ist, desto breiter ist das Konfidenzintervall.
## Hypothesentests
In unserem Datensatz der Baseballspieler gibt es verschiedene Spielerrollen, die wie folgt zusammengefasst werden können (sehen Sie sich das [begleitende Notebook](notebook.ipynb) an, um zu sehen, wie diese Tabelle berechnet werden kann):
| Rolle | Größe | Gewicht | Anzahl |
|-------|-------|---------|--------|
| Catcher | 72.723684 | 204.328947 | 76 |
| Designated_Hitter | 74.222222 | 220.888889 | 18 |
| First_Baseman | 74.000000 | 213.109091 | 55 |
| Outfielder | 73.010309 | 199.113402 | 194 |
| Relief_Pitcher | 74.374603 | 203.517460 | 315 |
| Second_Baseman | 71.362069 | 184.344828 | 58 |
| Shortstop | 71.903846 | 182.923077 | 52 |
| Starting_Pitcher | 74.719457 | 205.163636 | 221 |
| Third_Baseman | 73.044444 | 200.955556 | 45 |
Wir können feststellen, dass die durchschnittliche Größe der First Basemen höher ist als die der Second Basemen. Daher könnten wir versucht sein, zu folgern, dass **First Basemen größer sind als Second Basemen**.
> Diese Aussage wird als **Hypothese** bezeichnet, da wir nicht wissen, ob die Tatsache tatsächlich wahr ist oder nicht.
Es ist jedoch nicht immer offensichtlich, ob wir diese Schlussfolgerung ziehen können. Aus der obigen Diskussion wissen wir, dass jeder Mittelwert ein zugehöriges Konfidenzintervall hat, und daher könnte dieser Unterschied nur ein statistischer Fehler sein. Wir benötigen eine formellere Methode, um unsere Hypothese zu testen.
Lassen Sie uns die Konfidenzintervalle separat für die Größen der First und Second Basemen berechnen:
| Konfidenz | First Basemen | Second Basemen |
|-----------|---------------|----------------|
| 0.85 | 73.62..74.38 | 71.04..71.69 |
| 0.90 | 73.56..74.44 | 70.99..71.73 |
| 0.95 | 73.47..74.53 | 70.92..71.81 |
Wir können sehen, dass die Intervalle unter keiner Konfidenz überlappen. Das beweist unsere Hypothese, dass First Basemen größer sind als Second Basemen.
Formeller gesagt, das Problem, das wir lösen, besteht darin zu prüfen, ob **zwei Wahrscheinlichkeitsverteilungen gleich sind** oder zumindest die gleichen Parameter haben. Abhängig von der Verteilung müssen wir dafür unterschiedliche Tests verwenden. Wenn wir wissen, dass unsere Verteilungen normal sind, können wir den **[Student-t-Test](https://en.wikipedia.org/wiki/Student%27s_t-test)** anwenden.
Im Student-t-Test berechnen wir den sogenannten **t-Wert**, der den Unterschied zwischen den Mittelwerten unter Berücksichtigung der Varianz angibt. Es wird gezeigt, dass der t-Wert der **Student-Verteilung** folgt, was es uns ermöglicht, den Schwellenwert für ein gegebenes Konfidenzniveau **p** zu erhalten (dies kann berechnet oder in numerischen Tabellen nachgeschlagen werden). Wir vergleichen dann den t-Wert mit diesem Schwellenwert, um die Hypothese zu bestätigen oder abzulehnen.
In Python können wir das **SciPy**-Paket verwenden, das die Funktion `ttest_ind` enthält (zusätzlich zu vielen anderen nützlichen statistischen Funktionen!). Es berechnet den t-Wert für uns und führt auch die Rückwärtssuche des Konfidenz-p-Werts durch, sodass wir nur auf die Konfidenz schauen müssen, um eine Schlussfolgerung zu ziehen.
Zum Beispiel ergibt unser Vergleich zwischen den Größen der First und Second Basemen die folgenden Ergebnisse:
```python
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
```
```
T-value = 7.65
P-value: 9.137321189738925e-12
```
In unserem Fall ist der p-Wert sehr niedrig, was bedeutet, dass es starke Beweise dafür gibt, dass First Basemen größer sind.
Es gibt auch verschiedene andere Arten von Hypothesen, die wir testen könnten, zum Beispiel:
* Um zu beweisen, dass eine gegebene Stichprobe einer bestimmten Verteilung folgt. In unserem Fall haben wir angenommen, dass die Größen normal verteilt sind, aber das erfordert eine formale statistische Überprüfung.
* Um zu beweisen, dass der Mittelwert einer Stichprobe einem vordefinierten Wert entspricht.
* Um die Mittelwerte einer Anzahl von Stichproben zu vergleichen (z. B. den Unterschied in den Glücksniveaus zwischen verschiedenen Altersgruppen).
## Gesetz der großen Zahlen und zentraler Grenzwertsatz
Einer der Gründe, warum die Normalverteilung so wichtig ist, ist der sogenannte **zentrale Grenzwertsatz**. Angenommen, wir haben eine große Stichprobe von unabhängigen N Werten X1, ..., XN, die aus einer beliebigen Verteilung mit Mittelwert μ und Varianz σ2 entnommen wurden. Dann, für ausreichend großes N (mit anderen Worten, wenn N→∞), wird der Mittelwert ΣiXi normal verteilt sein, mit Mittelwert μ und Varianz σ2/N.
> Eine andere Möglichkeit, den zentralen Grenzwertsatz zu interpretieren, besteht darin zu sagen, dass unabhängig von der Verteilung, wenn Sie den Mittelwert einer Summe beliebiger Zufallsvariablen berechnen, Sie am Ende eine Normalverteilung erhalten.
Aus dem zentralen Grenzwertsatz folgt auch, dass, wenn N→∞, die Wahrscheinlichkeit, dass der Stichprobenmittelwert gleich μ ist, 1 wird. Dies ist als **Gesetz der großen Zahlen** bekannt.
## Kovarianz und Korrelation
Eine der Aufgaben der Datenwissenschaft besteht darin, Beziehungen zwischen Daten zu finden. Wir sagen, dass zwei Sequenzen **korrelieren**, wenn sie sich zur gleichen Zeit ähnlich verhalten, d.h. sie steigen/fallen gleichzeitig, oder eine Sequenz steigt, wenn die andere fällt und umgekehrt. Mit anderen Worten, es scheint eine Beziehung zwischen zwei Sequenzen zu geben.
> Korrelation zeigt nicht unbedingt eine kausale Beziehung zwischen zwei Sequenzen an; manchmal können beide Variablen von einer externen Ursache abhängen, oder es kann rein zufällig sein, dass die beiden Sequenzen korrelieren. Eine starke mathematische Korrelation ist jedoch ein guter Hinweis darauf, dass zwei Variablen irgendwie miteinander verbunden sind.
Mathematisch ist das Hauptkonzept, das die Beziehung zwischen zwei Zufallsvariablen zeigt, die **Kovarianz**, die wie folgt berechnet wird: Cov(X,Y) = **E**\[(X-**E**(X))(Y-**E**(Y))\]. Wir berechnen die Abweichung beider Variablen von ihren Mittelwerten und dann das Produkt dieser Abweichungen. Wenn beide Variablen zusammen abweichen, ist das Produkt immer ein positiver Wert, der zu einer positiven Kovarianz addiert wird. Wenn beide Variablen nicht synchron abweichen (d.h. eine fällt unter den Durchschnitt, wenn die andere über den Durchschnitt steigt), erhalten wir immer negative Zahlen, die zu einer negativen Kovarianz addiert werden. Wenn die Abweichungen unabhängig sind, summieren sie sich ungefähr zu null.
Der absolute Wert der Kovarianz sagt uns nicht viel darüber, wie groß die Korrelation ist, da er von der Größe der tatsächlichen Werte abhängt. Um sie zu normalisieren, können wir die Kovarianz durch die Standardabweichung beider Variablen teilen, um die **Korrelation** zu erhalten. Das Gute daran ist, dass die Korrelation immer im Bereich von [-1,1] liegt, wobei 1 eine starke positive Korrelation zwischen Werten anzeigt, -1 eine starke negative Korrelation und 0 keine Korrelation (Variablen sind unabhängig).
**Beispiel**: Wir können die Korrelation zwischen Gewichten und Größen von Baseballspielern aus dem oben genannten Datensatz berechnen:
```python
print(np.corrcoef(weights,heights))
```
Als Ergebnis erhalten wir eine **Korrelationsmatrix** wie diese:
```
array([[1. , 0.52959196],
[0.52959196, 1. ]])
```
> Die Korrelationsmatrix C kann für jede Anzahl von Eingabesequenzen S1, ..., Sn berechnet werden. Der Wert von Cij ist die Korrelation zwischen Si und Sj, und die Diagonalelemente sind immer 1 (was auch die Selbstkorrelation von Si ist).
In unserem Fall zeigt der Wert 0.53 an, dass es eine gewisse Korrelation zwischen dem Gewicht und der Größe einer Person gibt. Wir können auch das Streudiagramm eines Wertes gegen den anderen erstellen, um die Beziehung visuell zu sehen:
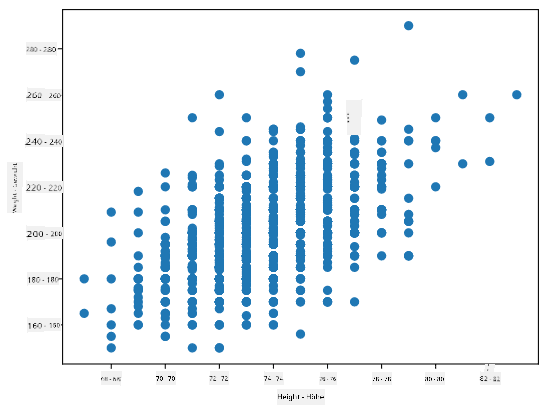
> Weitere Beispiele für Korrelation und Kovarianz finden Sie im [begleitenden Notebook](notebook.ipynb).
## Fazit
In diesem Abschnitt haben wir gelernt:
* grundlegende statistische Eigenschaften von Daten, wie Mittelwert, Varianz, Modus und Quartile
* verschiedene Verteilungen von Zufallsvariablen, einschließlich der Normalverteilung
* wie man Korrelationen zwischen verschiedenen Eigenschaften findet
* wie man mathematische und statistische Methoden verwendet, um Hypothesen zu beweisen
* wie man Konfidenzintervalle für Zufallsvariablen basierend auf Stichprobendaten berechnet
Obwohl dies definitiv keine vollständige Liste der Themen ist, die innerhalb der Wahrscheinlichkeit und Statistik existieren, sollte es ausreichen, um Ihnen einen guten Einstieg in diesen Kurs zu geben.
## 🚀 Herausforderung
Verwenden Sie den Beispielcode im Notebook, um andere Hypothesen zu testen:
1. First Basemen sind älter als Second Basemen
2. First Basemen sind größer als Third Basemen
3. Shortstops sind größer als Second Basemen
## [Quiz nach der Vorlesung](https://ff-quizzes.netlify.app/en/ds/quiz/7)
## Überprüfung & Selbststudium
Wahrscheinlichkeit und Statistik ist ein so breites Thema, dass es einen eigenen Kurs verdient. Wenn Sie tiefer in die Theorie eintauchen möchten, können Sie einige der folgenden Bücher lesen:
1. [Carlos Fernandez-Granda](https://cims.nyu.edu/~cfgranda/) von der New York University hat großartige Vorlesungsnotizen [Probability and Statistics for Data Science](https://cims.nyu.edu/~cfgranda/pages/stuff/probability_stats_for_DS.pdf) (online verfügbar)
1. [Peter und Andrew Bruce. Practical Statistics for Data Scientists.](https://www.oreilly.com/library/view/practical-statistics-for/9781491952955/) [[Beispielcode in R](https://github.com/andrewgbruce/statistics-for-data-scientists)].
1. [James D. Miller. Statistics for Data Science](https://www.packtpub.com/product/statistics-for-data-science/9781788290678) [[Beispielcode in R](https://github.com/PacktPublishing/Statistics-for-Data-Science)]
## Aufgabe
[Kleine Diabetes-Studie](assignment.md)
## Credits
Diese Lektion wurde mit ♥️ von [Dmitry Soshnikov](http://soshnikov.com) erstellt.
---
**Haftungsausschluss**:
Dieses Dokument wurde mithilfe des KI-Übersetzungsdienstes [Co-op Translator](https://github.com/Azure/co-op-translator) übersetzt. Obwohl wir uns um Genauigkeit bemühen, weisen wir darauf hin, dass automatisierte Übersetzungen Fehler oder Ungenauigkeiten enthalten können. Das Originaldokument in seiner ursprünglichen Sprache sollte als maßgebliche Quelle betrachtet werden. Für kritische Informationen wird eine professionelle menschliche Übersetzung empfohlen. Wir übernehmen keine Haftung für Missverständnisse oder Fehlinterpretationen, die aus der Nutzung dieser Übersetzung entstehen.
Hier berechnen wir auch den **Interquartilsabstand** IQR=Q3-Q1 und sogenannte **Ausreißer** – Werte, die außerhalb der Grenzen [Q1-1.5*IQR, Q3+1.5*IQR] liegen.
Für eine endliche Verteilung, die nur eine kleine Anzahl möglicher Werte enthält, ist ein guter "typischer" Wert derjenige, der am häufigsten vorkommt, der sogenannte **Modus**. Er wird oft auf kategoriale Daten angewendet, wie z. B. Farben. Betrachten Sie eine Situation, in der wir zwei Gruppen von Menschen haben – einige, die stark Rot bevorzugen, und andere, die Blau bevorzugen. Wenn wir Farben durch Zahlen kodieren, würde der Mittelwert für die Lieblingsfarbe irgendwo im orange-grünen Spektrum liegen, was die tatsächliche Präferenz keiner der Gruppen widerspiegelt. Der Modus hingegen wäre entweder eine der Farben oder beide Farben, wenn die Anzahl der Personen, die für sie stimmen, gleich ist (in diesem Fall nennen wir die Stichprobe **multimodal**).
## Reale Daten
Wenn wir Daten aus der realen Welt analysieren, sind sie oft keine Zufallsvariablen im eigentlichen Sinne, da wir keine Experimente mit unbekanntem Ergebnis durchführen. Betrachten Sie zum Beispiel ein Team von Baseballspielern und deren Körperdaten wie Größe, Gewicht und Alter. Diese Zahlen sind nicht wirklich zufällig, aber wir können dennoch dieselben mathematischen Konzepte anwenden. Zum Beispiel kann eine Sequenz von Gewichten von Personen als eine Sequenz von Werten betrachtet werden, die aus einer Zufallsvariablen gezogen wurden. Unten sehen Sie die Gewichtssequenz tatsächlicher Baseballspieler aus der [Major League Baseball](http://mlb.mlb.com/index.jsp), entnommen aus [diesem Datensatz](http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_MLB_HeightsWeights) (der Übersicht halber sind nur die ersten 20 Werte dargestellt):
```
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
```
> **Hinweis**: Um ein Beispiel für die Arbeit mit diesem Datensatz zu sehen, werfen Sie einen Blick auf das [begleitende Notebook](notebook.ipynb). Es gibt auch eine Reihe von Herausforderungen in dieser Lektion, die Sie durch das Hinzufügen von Code zu diesem Notebook abschließen können. Wenn Sie nicht sicher sind, wie man mit Daten arbeitet, machen Sie sich keine Sorgen – wir werden später darauf zurückkommen, wie man mit Python arbeitet. Wenn Sie nicht wissen, wie man Code in einem Jupyter Notebook ausführt, lesen Sie [diesen Artikel](https://soshnikov.com/education/how-to-execute-notebooks-from-github/).
Hier ist der Boxplot, der Mittelwert, Median und Quartile für unsere Daten zeigt:

Da unsere Daten Informationen über verschiedene Spieler**rollen** enthalten, können wir auch den Boxplot nach Rollen erstellen – so können wir erkennen, wie sich die Parameterwerte je nach Rolle unterscheiden. Diesmal betrachten wir die Größe:

Dieses Diagramm deutet darauf hin, dass die Größe von First Basemen im Durchschnitt höher ist als die von Second Basemen. Später in dieser Lektion werden wir lernen, wie wir diese Hypothese formeller testen können und wie wir zeigen können, dass unsere Daten statistisch signifikant sind, um dies zu belegen.
> Wenn wir mit realen Daten arbeiten, gehen wir davon aus, dass alle Datenpunkte Stichproben sind, die aus einer Wahrscheinlichkeitsverteilung gezogen wurden. Diese Annahme ermöglicht es uns, maschinelles Lernen anzuwenden und funktionierende Vorhersagemodelle zu erstellen.
Um zu sehen, wie die Verteilung unserer Daten aussieht, können wir ein Diagramm namens **Histogramm** erstellen. Die X-Achse enthält eine Anzahl verschiedener Gewichtsintervalle (sogenannte **Bins**), und die Y-Achse zeigt die Anzahl der Male, die unsere Zufallsvariablenstichprobe in ein bestimmtes Intervall fiel.

Aus diesem Histogramm können Sie erkennen, dass alle Werte um einen bestimmten mittleren Wert zentriert sind und dass die Wahrscheinlichkeit, dass ein Gewicht stark vom Mittelwert abweicht, geringer ist. Die Varianz der Gewichte zeigt, in welchem Maße die Gewichte wahrscheinlich vom Mittelwert abweichen.
> Wenn wir die Gewichte anderer Personen, die nicht aus der Baseballliga stammen, betrachten, ist die Verteilung wahrscheinlich anders. Die Form der Verteilung bleibt jedoch gleich, aber Mittelwert und Varianz ändern sich. Wenn wir unser Modell auf Baseballspieler trainieren, wird es wahrscheinlich falsche Ergebnisse liefern, wenn es auf Universitätsstudenten angewendet wird, da die zugrunde liegende Verteilung unterschiedlich ist.
## Normalverteilung
Die Verteilung der Gewichte, die wir oben gesehen haben, ist sehr typisch, und viele Messungen aus der realen Welt folgen demselben Verteilungstyp, jedoch mit unterschiedlichem Mittelwert und Varianz. Diese Verteilung wird als **Normalverteilung** bezeichnet und spielt eine sehr wichtige Rolle in der Statistik.
Die Verwendung der Normalverteilung ist eine korrekte Methode, um zufällige Gewichte potenzieller Baseballspieler zu generieren. Sobald wir den mittleren Wert `mean` und die Standardabweichung `std` kennen, können wir 1000 Gewichtsstichproben wie folgt generieren:
```python
samples = np.random.normal(mean,std,1000)
```
Wenn wir das Histogramm der generierten Stichproben zeichnen, sehen wir ein Bild, das dem oben gezeigten sehr ähnlich ist. Und wenn wir die Anzahl der Stichproben und die Anzahl der Bins erhöhen, können wir ein Bild einer Normalverteilung erzeugen, das näher an der idealen Form liegt:

*Normalverteilung mit Mittelwert=0 und Standardabweichung=1*
## Konfidenzintervalle
Wenn wir über die Gewichte von Baseballspielern sprechen, nehmen wir an, dass es eine bestimmte **Zufallsvariable W** gibt, die der idealen Wahrscheinlichkeitsverteilung der Gewichte aller Baseballspieler entspricht (sogenannte **Population**). Unsere Gewichtssequenz entspricht einer Teilmenge aller Baseballspieler, die wir als **Stichprobe** bezeichnen. Eine interessante Frage ist: Können wir die Parameter der Verteilung von W kennen, d. h. den Mittelwert und die Varianz der Population?
Die einfachste Antwort wäre, den Mittelwert und die Varianz unserer Stichprobe zu berechnen. Es könnte jedoch sein, dass unsere zufällige Stichprobe die gesamte Population nicht genau repräsentiert. Daher macht es Sinn, über **Konfidenzintervalle** zu sprechen.
> **Konfidenzintervall** ist die Schätzung des tatsächlichen Mittelwerts der Population basierend auf unserer Stichprobe, die mit einer bestimmten Wahrscheinlichkeit (oder **Konfidenzniveau**) korrekt ist.
Angenommen, wir haben eine Stichprobe X...
1, ..., Xn aus unserer Verteilung. Jedes Mal, wenn wir eine Stichprobe aus unserer Verteilung ziehen, erhalten wir einen anderen Mittelwert μ. Daher kann μ als Zufallsvariable betrachtet werden. Ein **Konfidenzintervall** mit Konfidenz p ist ein Wertepaar (Lp,Rp), sodass **P**(Lp≤μ≤Rp) = p, d.h. die Wahrscheinlichkeit, dass der gemessene Mittelwert innerhalb des Intervalls liegt, entspricht p.
Es geht über unsere kurze Einführung hinaus, im Detail zu erklären, wie diese Konfidenzintervalle berechnet werden. Weitere Details finden Sie [auf Wikipedia](https://en.wikipedia.org/wiki/Confidence_interval). Kurz gesagt, wir definieren die Verteilung des berechneten Stichprobenmittelwerts relativ zum wahren Mittelwert der Population, die als **Student-Verteilung** bezeichnet wird.
> **Interessante Tatsache**: Die Student-Verteilung ist nach dem Mathematiker William Sealy Gosset benannt, der seine Arbeit unter dem Pseudonym "Student" veröffentlichte. Er arbeitete in der Guinness-Brauerei, und laut einer Version wollte sein Arbeitgeber nicht, dass die Öffentlichkeit erfährt, dass sie statistische Tests zur Bestimmung der Qualität der Rohstoffe verwendeten.
Wenn wir den Mittelwert μ unserer Population mit Konfidenz p schätzen möchten, müssen wir das *(1-p)/2-te Perzentil* einer Student-Verteilung A nehmen, das entweder aus Tabellen entnommen oder mithilfe eingebauter Funktionen statistischer Software (z. B. Python, R usw.) berechnet werden kann. Dann wird das Intervall für μ durch X±A*D/√n gegeben, wobei X der erhaltene Mittelwert der Stichprobe und D die Standardabweichung ist.
> **Hinweis**: Wir lassen auch die Diskussion über ein wichtiges Konzept der [Freiheitsgrade](https://en.wikipedia.org/wiki/Degrees_of_freedom_(statistics)) aus, das im Zusammenhang mit der Student-Verteilung wichtig ist. Sie können auf umfassendere Bücher über Statistik zurückgreifen, um dieses Konzept tiefer zu verstehen.
Ein Beispiel für die Berechnung des Konfidenzintervalls für Gewichte und Größen finden Sie in den [begleitenden Notebooks](notebook.ipynb).
| p | Gewichtsmittelwert |
|-----|------------------|
| 0.85 | 201.73±0.94 |
| 0.90 | 201.73±1.08 |
| 0.95 | 201.73±1.28 |
Beachten Sie, dass je höher die Konfidenzwahrscheinlichkeit ist, desto breiter ist das Konfidenzintervall.
## Hypothesentests
In unserem Datensatz der Baseballspieler gibt es verschiedene Spielerrollen, die wie folgt zusammengefasst werden können (sehen Sie sich das [begleitende Notebook](notebook.ipynb) an, um zu sehen, wie diese Tabelle berechnet werden kann):
| Rolle | Größe | Gewicht | Anzahl |
|-------|-------|---------|--------|
| Catcher | 72.723684 | 204.328947 | 76 |
| Designated_Hitter | 74.222222 | 220.888889 | 18 |
| First_Baseman | 74.000000 | 213.109091 | 55 |
| Outfielder | 73.010309 | 199.113402 | 194 |
| Relief_Pitcher | 74.374603 | 203.517460 | 315 |
| Second_Baseman | 71.362069 | 184.344828 | 58 |
| Shortstop | 71.903846 | 182.923077 | 52 |
| Starting_Pitcher | 74.719457 | 205.163636 | 221 |
| Third_Baseman | 73.044444 | 200.955556 | 45 |
Wir können feststellen, dass die durchschnittliche Größe der First Basemen höher ist als die der Second Basemen. Daher könnten wir versucht sein, zu folgern, dass **First Basemen größer sind als Second Basemen**.
> Diese Aussage wird als **Hypothese** bezeichnet, da wir nicht wissen, ob die Tatsache tatsächlich wahr ist oder nicht.
Es ist jedoch nicht immer offensichtlich, ob wir diese Schlussfolgerung ziehen können. Aus der obigen Diskussion wissen wir, dass jeder Mittelwert ein zugehöriges Konfidenzintervall hat, und daher könnte dieser Unterschied nur ein statistischer Fehler sein. Wir benötigen eine formellere Methode, um unsere Hypothese zu testen.
Lassen Sie uns die Konfidenzintervalle separat für die Größen der First und Second Basemen berechnen:
| Konfidenz | First Basemen | Second Basemen |
|-----------|---------------|----------------|
| 0.85 | 73.62..74.38 | 71.04..71.69 |
| 0.90 | 73.56..74.44 | 70.99..71.73 |
| 0.95 | 73.47..74.53 | 70.92..71.81 |
Wir können sehen, dass die Intervalle unter keiner Konfidenz überlappen. Das beweist unsere Hypothese, dass First Basemen größer sind als Second Basemen.
Formeller gesagt, das Problem, das wir lösen, besteht darin zu prüfen, ob **zwei Wahrscheinlichkeitsverteilungen gleich sind** oder zumindest die gleichen Parameter haben. Abhängig von der Verteilung müssen wir dafür unterschiedliche Tests verwenden. Wenn wir wissen, dass unsere Verteilungen normal sind, können wir den **[Student-t-Test](https://en.wikipedia.org/wiki/Student%27s_t-test)** anwenden.
Im Student-t-Test berechnen wir den sogenannten **t-Wert**, der den Unterschied zwischen den Mittelwerten unter Berücksichtigung der Varianz angibt. Es wird gezeigt, dass der t-Wert der **Student-Verteilung** folgt, was es uns ermöglicht, den Schwellenwert für ein gegebenes Konfidenzniveau **p** zu erhalten (dies kann berechnet oder in numerischen Tabellen nachgeschlagen werden). Wir vergleichen dann den t-Wert mit diesem Schwellenwert, um die Hypothese zu bestätigen oder abzulehnen.
In Python können wir das **SciPy**-Paket verwenden, das die Funktion `ttest_ind` enthält (zusätzlich zu vielen anderen nützlichen statistischen Funktionen!). Es berechnet den t-Wert für uns und führt auch die Rückwärtssuche des Konfidenz-p-Werts durch, sodass wir nur auf die Konfidenz schauen müssen, um eine Schlussfolgerung zu ziehen.
Zum Beispiel ergibt unser Vergleich zwischen den Größen der First und Second Basemen die folgenden Ergebnisse:
```python
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
```
```
T-value = 7.65
P-value: 9.137321189738925e-12
```
In unserem Fall ist der p-Wert sehr niedrig, was bedeutet, dass es starke Beweise dafür gibt, dass First Basemen größer sind.
Es gibt auch verschiedene andere Arten von Hypothesen, die wir testen könnten, zum Beispiel:
* Um zu beweisen, dass eine gegebene Stichprobe einer bestimmten Verteilung folgt. In unserem Fall haben wir angenommen, dass die Größen normal verteilt sind, aber das erfordert eine formale statistische Überprüfung.
* Um zu beweisen, dass der Mittelwert einer Stichprobe einem vordefinierten Wert entspricht.
* Um die Mittelwerte einer Anzahl von Stichproben zu vergleichen (z. B. den Unterschied in den Glücksniveaus zwischen verschiedenen Altersgruppen).
## Gesetz der großen Zahlen und zentraler Grenzwertsatz
Einer der Gründe, warum die Normalverteilung so wichtig ist, ist der sogenannte **zentrale Grenzwertsatz**. Angenommen, wir haben eine große Stichprobe von unabhängigen N Werten X1, ..., XN, die aus einer beliebigen Verteilung mit Mittelwert μ und Varianz σ2 entnommen wurden. Dann, für ausreichend großes N (mit anderen Worten, wenn N→∞), wird der Mittelwert ΣiXi normal verteilt sein, mit Mittelwert μ und Varianz σ2/N.
> Eine andere Möglichkeit, den zentralen Grenzwertsatz zu interpretieren, besteht darin zu sagen, dass unabhängig von der Verteilung, wenn Sie den Mittelwert einer Summe beliebiger Zufallsvariablen berechnen, Sie am Ende eine Normalverteilung erhalten.
Aus dem zentralen Grenzwertsatz folgt auch, dass, wenn N→∞, die Wahrscheinlichkeit, dass der Stichprobenmittelwert gleich μ ist, 1 wird. Dies ist als **Gesetz der großen Zahlen** bekannt.
## Kovarianz und Korrelation
Eine der Aufgaben der Datenwissenschaft besteht darin, Beziehungen zwischen Daten zu finden. Wir sagen, dass zwei Sequenzen **korrelieren**, wenn sie sich zur gleichen Zeit ähnlich verhalten, d.h. sie steigen/fallen gleichzeitig, oder eine Sequenz steigt, wenn die andere fällt und umgekehrt. Mit anderen Worten, es scheint eine Beziehung zwischen zwei Sequenzen zu geben.
> Korrelation zeigt nicht unbedingt eine kausale Beziehung zwischen zwei Sequenzen an; manchmal können beide Variablen von einer externen Ursache abhängen, oder es kann rein zufällig sein, dass die beiden Sequenzen korrelieren. Eine starke mathematische Korrelation ist jedoch ein guter Hinweis darauf, dass zwei Variablen irgendwie miteinander verbunden sind.
Mathematisch ist das Hauptkonzept, das die Beziehung zwischen zwei Zufallsvariablen zeigt, die **Kovarianz**, die wie folgt berechnet wird: Cov(X,Y) = **E**\[(X-**E**(X))(Y-**E**(Y))\]. Wir berechnen die Abweichung beider Variablen von ihren Mittelwerten und dann das Produkt dieser Abweichungen. Wenn beide Variablen zusammen abweichen, ist das Produkt immer ein positiver Wert, der zu einer positiven Kovarianz addiert wird. Wenn beide Variablen nicht synchron abweichen (d.h. eine fällt unter den Durchschnitt, wenn die andere über den Durchschnitt steigt), erhalten wir immer negative Zahlen, die zu einer negativen Kovarianz addiert werden. Wenn die Abweichungen unabhängig sind, summieren sie sich ungefähr zu null.
Der absolute Wert der Kovarianz sagt uns nicht viel darüber, wie groß die Korrelation ist, da er von der Größe der tatsächlichen Werte abhängt. Um sie zu normalisieren, können wir die Kovarianz durch die Standardabweichung beider Variablen teilen, um die **Korrelation** zu erhalten. Das Gute daran ist, dass die Korrelation immer im Bereich von [-1,1] liegt, wobei 1 eine starke positive Korrelation zwischen Werten anzeigt, -1 eine starke negative Korrelation und 0 keine Korrelation (Variablen sind unabhängig).
**Beispiel**: Wir können die Korrelation zwischen Gewichten und Größen von Baseballspielern aus dem oben genannten Datensatz berechnen:
```python
print(np.corrcoef(weights,heights))
```
Als Ergebnis erhalten wir eine **Korrelationsmatrix** wie diese:
```
array([[1. , 0.52959196],
[0.52959196, 1. ]])
```
> Die Korrelationsmatrix C kann für jede Anzahl von Eingabesequenzen S1, ..., Sn berechnet werden. Der Wert von Cij ist die Korrelation zwischen Si und Sj, und die Diagonalelemente sind immer 1 (was auch die Selbstkorrelation von Si ist).
In unserem Fall zeigt der Wert 0.53 an, dass es eine gewisse Korrelation zwischen dem Gewicht und der Größe einer Person gibt. Wir können auch das Streudiagramm eines Wertes gegen den anderen erstellen, um die Beziehung visuell zu sehen:

> Weitere Beispiele für Korrelation und Kovarianz finden Sie im [begleitenden Notebook](notebook.ipynb).
## Fazit
In diesem Abschnitt haben wir gelernt:
* grundlegende statistische Eigenschaften von Daten, wie Mittelwert, Varianz, Modus und Quartile
* verschiedene Verteilungen von Zufallsvariablen, einschließlich der Normalverteilung
* wie man Korrelationen zwischen verschiedenen Eigenschaften findet
* wie man mathematische und statistische Methoden verwendet, um Hypothesen zu beweisen
* wie man Konfidenzintervalle für Zufallsvariablen basierend auf Stichprobendaten berechnet
Obwohl dies definitiv keine vollständige Liste der Themen ist, die innerhalb der Wahrscheinlichkeit und Statistik existieren, sollte es ausreichen, um Ihnen einen guten Einstieg in diesen Kurs zu geben.
## 🚀 Herausforderung
Verwenden Sie den Beispielcode im Notebook, um andere Hypothesen zu testen:
1. First Basemen sind älter als Second Basemen
2. First Basemen sind größer als Third Basemen
3. Shortstops sind größer als Second Basemen
## [Quiz nach der Vorlesung](https://ff-quizzes.netlify.app/en/ds/quiz/7)
## Überprüfung & Selbststudium
Wahrscheinlichkeit und Statistik ist ein so breites Thema, dass es einen eigenen Kurs verdient. Wenn Sie tiefer in die Theorie eintauchen möchten, können Sie einige der folgenden Bücher lesen:
1. [Carlos Fernandez-Granda](https://cims.nyu.edu/~cfgranda/) von der New York University hat großartige Vorlesungsnotizen [Probability and Statistics for Data Science](https://cims.nyu.edu/~cfgranda/pages/stuff/probability_stats_for_DS.pdf) (online verfügbar)
1. [Peter und Andrew Bruce. Practical Statistics for Data Scientists.](https://www.oreilly.com/library/view/practical-statistics-for/9781491952955/) [[Beispielcode in R](https://github.com/andrewgbruce/statistics-for-data-scientists)].
1. [James D. Miller. Statistics for Data Science](https://www.packtpub.com/product/statistics-for-data-science/9781788290678) [[Beispielcode in R](https://github.com/PacktPublishing/Statistics-for-Data-Science)]
## Aufgabe
[Kleine Diabetes-Studie](assignment.md)
## Credits
Diese Lektion wurde mit ♥️ von [Dmitry Soshnikov](http://soshnikov.com) erstellt.
---
**Haftungsausschluss**:
Dieses Dokument wurde mithilfe des KI-Übersetzungsdienstes [Co-op Translator](https://github.com/Azure/co-op-translator) übersetzt. Obwohl wir uns um Genauigkeit bemühen, weisen wir darauf hin, dass automatisierte Übersetzungen Fehler oder Ungenauigkeiten enthalten können. Das Originaldokument in seiner ursprünglichen Sprache sollte als maßgebliche Quelle betrachtet werden. Für kritische Informationen wird eine professionelle menschliche Übersetzung empfohlen. Wir übernehmen keine Haftung für Missverständnisse oder Fehlinterpretationen, die aus der Nutzung dieser Übersetzung entstehen. Hier berechnen wir auch den **Interquartilsabstand** IQR=Q3-Q1 und sogenannte **Ausreißer** – Werte, die außerhalb der Grenzen [Q1-1.5*IQR, Q3+1.5*IQR] liegen.
Für eine endliche Verteilung, die nur eine kleine Anzahl möglicher Werte enthält, ist ein guter "typischer" Wert derjenige, der am häufigsten vorkommt, der sogenannte **Modus**. Er wird oft auf kategoriale Daten angewendet, wie z. B. Farben. Betrachten Sie eine Situation, in der wir zwei Gruppen von Menschen haben – einige, die stark Rot bevorzugen, und andere, die Blau bevorzugen. Wenn wir Farben durch Zahlen kodieren, würde der Mittelwert für die Lieblingsfarbe irgendwo im orange-grünen Spektrum liegen, was die tatsächliche Präferenz keiner der Gruppen widerspiegelt. Der Modus hingegen wäre entweder eine der Farben oder beide Farben, wenn die Anzahl der Personen, die für sie stimmen, gleich ist (in diesem Fall nennen wir die Stichprobe **multimodal**).
## Reale Daten
Wenn wir Daten aus der realen Welt analysieren, sind sie oft keine Zufallsvariablen im eigentlichen Sinne, da wir keine Experimente mit unbekanntem Ergebnis durchführen. Betrachten Sie zum Beispiel ein Team von Baseballspielern und deren Körperdaten wie Größe, Gewicht und Alter. Diese Zahlen sind nicht wirklich zufällig, aber wir können dennoch dieselben mathematischen Konzepte anwenden. Zum Beispiel kann eine Sequenz von Gewichten von Personen als eine Sequenz von Werten betrachtet werden, die aus einer Zufallsvariablen gezogen wurden. Unten sehen Sie die Gewichtssequenz tatsächlicher Baseballspieler aus der [Major League Baseball](http://mlb.mlb.com/index.jsp), entnommen aus [diesem Datensatz](http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_MLB_HeightsWeights) (der Übersicht halber sind nur die ersten 20 Werte dargestellt):
```
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
```
> **Hinweis**: Um ein Beispiel für die Arbeit mit diesem Datensatz zu sehen, werfen Sie einen Blick auf das [begleitende Notebook](notebook.ipynb). Es gibt auch eine Reihe von Herausforderungen in dieser Lektion, die Sie durch das Hinzufügen von Code zu diesem Notebook abschließen können. Wenn Sie nicht sicher sind, wie man mit Daten arbeitet, machen Sie sich keine Sorgen – wir werden später darauf zurückkommen, wie man mit Python arbeitet. Wenn Sie nicht wissen, wie man Code in einem Jupyter Notebook ausführt, lesen Sie [diesen Artikel](https://soshnikov.com/education/how-to-execute-notebooks-from-github/).
Hier ist der Boxplot, der Mittelwert, Median und Quartile für unsere Daten zeigt:

Da unsere Daten Informationen über verschiedene Spieler**rollen** enthalten, können wir auch den Boxplot nach Rollen erstellen – so können wir erkennen, wie sich die Parameterwerte je nach Rolle unterscheiden. Diesmal betrachten wir die Größe:

Dieses Diagramm deutet darauf hin, dass die Größe von First Basemen im Durchschnitt höher ist als die von Second Basemen. Später in dieser Lektion werden wir lernen, wie wir diese Hypothese formeller testen können und wie wir zeigen können, dass unsere Daten statistisch signifikant sind, um dies zu belegen.
> Wenn wir mit realen Daten arbeiten, gehen wir davon aus, dass alle Datenpunkte Stichproben sind, die aus einer Wahrscheinlichkeitsverteilung gezogen wurden. Diese Annahme ermöglicht es uns, maschinelles Lernen anzuwenden und funktionierende Vorhersagemodelle zu erstellen.
Um zu sehen, wie die Verteilung unserer Daten aussieht, können wir ein Diagramm namens **Histogramm** erstellen. Die X-Achse enthält eine Anzahl verschiedener Gewichtsintervalle (sogenannte **Bins**), und die Y-Achse zeigt die Anzahl der Male, die unsere Zufallsvariablenstichprobe in ein bestimmtes Intervall fiel.

Aus diesem Histogramm können Sie erkennen, dass alle Werte um einen bestimmten mittleren Wert zentriert sind und dass die Wahrscheinlichkeit, dass ein Gewicht stark vom Mittelwert abweicht, geringer ist. Die Varianz der Gewichte zeigt, in welchem Maße die Gewichte wahrscheinlich vom Mittelwert abweichen.
> Wenn wir die Gewichte anderer Personen, die nicht aus der Baseballliga stammen, betrachten, ist die Verteilung wahrscheinlich anders. Die Form der Verteilung bleibt jedoch gleich, aber Mittelwert und Varianz ändern sich. Wenn wir unser Modell auf Baseballspieler trainieren, wird es wahrscheinlich falsche Ergebnisse liefern, wenn es auf Universitätsstudenten angewendet wird, da die zugrunde liegende Verteilung unterschiedlich ist.
## Normalverteilung
Die Verteilung der Gewichte, die wir oben gesehen haben, ist sehr typisch, und viele Messungen aus der realen Welt folgen demselben Verteilungstyp, jedoch mit unterschiedlichem Mittelwert und Varianz. Diese Verteilung wird als **Normalverteilung** bezeichnet und spielt eine sehr wichtige Rolle in der Statistik.
Die Verwendung der Normalverteilung ist eine korrekte Methode, um zufällige Gewichte potenzieller Baseballspieler zu generieren. Sobald wir den mittleren Wert `mean` und die Standardabweichung `std` kennen, können wir 1000 Gewichtsstichproben wie folgt generieren:
```python
samples = np.random.normal(mean,std,1000)
```
Wenn wir das Histogramm der generierten Stichproben zeichnen, sehen wir ein Bild, das dem oben gezeigten sehr ähnlich ist. Und wenn wir die Anzahl der Stichproben und die Anzahl der Bins erhöhen, können wir ein Bild einer Normalverteilung erzeugen, das näher an der idealen Form liegt:

*Normalverteilung mit Mittelwert=0 und Standardabweichung=1*
## Konfidenzintervalle
Wenn wir über die Gewichte von Baseballspielern sprechen, nehmen wir an, dass es eine bestimmte **Zufallsvariable W** gibt, die der idealen Wahrscheinlichkeitsverteilung der Gewichte aller Baseballspieler entspricht (sogenannte **Population**). Unsere Gewichtssequenz entspricht einer Teilmenge aller Baseballspieler, die wir als **Stichprobe** bezeichnen. Eine interessante Frage ist: Können wir die Parameter der Verteilung von W kennen, d. h. den Mittelwert und die Varianz der Population?
Die einfachste Antwort wäre, den Mittelwert und die Varianz unserer Stichprobe zu berechnen. Es könnte jedoch sein, dass unsere zufällige Stichprobe die gesamte Population nicht genau repräsentiert. Daher macht es Sinn, über **Konfidenzintervalle** zu sprechen.
> **Konfidenzintervall** ist die Schätzung des tatsächlichen Mittelwerts der Population basierend auf unserer Stichprobe, die mit einer bestimmten Wahrscheinlichkeit (oder **Konfidenzniveau**) korrekt ist.
Angenommen, wir haben eine Stichprobe X...
1, ..., Xn aus unserer Verteilung. Jedes Mal, wenn wir eine Stichprobe aus unserer Verteilung ziehen, erhalten wir einen anderen Mittelwert μ. Daher kann μ als Zufallsvariable betrachtet werden. Ein **Konfidenzintervall** mit Konfidenz p ist ein Wertepaar (Lp,Rp), sodass **P**(Lp≤μ≤Rp) = p, d.h. die Wahrscheinlichkeit, dass der gemessene Mittelwert innerhalb des Intervalls liegt, entspricht p.
Es geht über unsere kurze Einführung hinaus, im Detail zu erklären, wie diese Konfidenzintervalle berechnet werden. Weitere Details finden Sie [auf Wikipedia](https://en.wikipedia.org/wiki/Confidence_interval). Kurz gesagt, wir definieren die Verteilung des berechneten Stichprobenmittelwerts relativ zum wahren Mittelwert der Population, die als **Student-Verteilung** bezeichnet wird.
> **Interessante Tatsache**: Die Student-Verteilung ist nach dem Mathematiker William Sealy Gosset benannt, der seine Arbeit unter dem Pseudonym "Student" veröffentlichte. Er arbeitete in der Guinness-Brauerei, und laut einer Version wollte sein Arbeitgeber nicht, dass die Öffentlichkeit erfährt, dass sie statistische Tests zur Bestimmung der Qualität der Rohstoffe verwendeten.
Wenn wir den Mittelwert μ unserer Population mit Konfidenz p schätzen möchten, müssen wir das *(1-p)/2-te Perzentil* einer Student-Verteilung A nehmen, das entweder aus Tabellen entnommen oder mithilfe eingebauter Funktionen statistischer Software (z. B. Python, R usw.) berechnet werden kann. Dann wird das Intervall für μ durch X±A*D/√n gegeben, wobei X der erhaltene Mittelwert der Stichprobe und D die Standardabweichung ist.
> **Hinweis**: Wir lassen auch die Diskussion über ein wichtiges Konzept der [Freiheitsgrade](https://en.wikipedia.org/wiki/Degrees_of_freedom_(statistics)) aus, das im Zusammenhang mit der Student-Verteilung wichtig ist. Sie können auf umfassendere Bücher über Statistik zurückgreifen, um dieses Konzept tiefer zu verstehen.
Ein Beispiel für die Berechnung des Konfidenzintervalls für Gewichte und Größen finden Sie in den [begleitenden Notebooks](notebook.ipynb).
| p | Gewichtsmittelwert |
|-----|------------------|
| 0.85 | 201.73±0.94 |
| 0.90 | 201.73±1.08 |
| 0.95 | 201.73±1.28 |
Beachten Sie, dass je höher die Konfidenzwahrscheinlichkeit ist, desto breiter ist das Konfidenzintervall.
## Hypothesentests
In unserem Datensatz der Baseballspieler gibt es verschiedene Spielerrollen, die wie folgt zusammengefasst werden können (sehen Sie sich das [begleitende Notebook](notebook.ipynb) an, um zu sehen, wie diese Tabelle berechnet werden kann):
| Rolle | Größe | Gewicht | Anzahl |
|-------|-------|---------|--------|
| Catcher | 72.723684 | 204.328947 | 76 |
| Designated_Hitter | 74.222222 | 220.888889 | 18 |
| First_Baseman | 74.000000 | 213.109091 | 55 |
| Outfielder | 73.010309 | 199.113402 | 194 |
| Relief_Pitcher | 74.374603 | 203.517460 | 315 |
| Second_Baseman | 71.362069 | 184.344828 | 58 |
| Shortstop | 71.903846 | 182.923077 | 52 |
| Starting_Pitcher | 74.719457 | 205.163636 | 221 |
| Third_Baseman | 73.044444 | 200.955556 | 45 |
Wir können feststellen, dass die durchschnittliche Größe der First Basemen höher ist als die der Second Basemen. Daher könnten wir versucht sein, zu folgern, dass **First Basemen größer sind als Second Basemen**.
> Diese Aussage wird als **Hypothese** bezeichnet, da wir nicht wissen, ob die Tatsache tatsächlich wahr ist oder nicht.
Es ist jedoch nicht immer offensichtlich, ob wir diese Schlussfolgerung ziehen können. Aus der obigen Diskussion wissen wir, dass jeder Mittelwert ein zugehöriges Konfidenzintervall hat, und daher könnte dieser Unterschied nur ein statistischer Fehler sein. Wir benötigen eine formellere Methode, um unsere Hypothese zu testen.
Lassen Sie uns die Konfidenzintervalle separat für die Größen der First und Second Basemen berechnen:
| Konfidenz | First Basemen | Second Basemen |
|-----------|---------------|----------------|
| 0.85 | 73.62..74.38 | 71.04..71.69 |
| 0.90 | 73.56..74.44 | 70.99..71.73 |
| 0.95 | 73.47..74.53 | 70.92..71.81 |
Wir können sehen, dass die Intervalle unter keiner Konfidenz überlappen. Das beweist unsere Hypothese, dass First Basemen größer sind als Second Basemen.
Formeller gesagt, das Problem, das wir lösen, besteht darin zu prüfen, ob **zwei Wahrscheinlichkeitsverteilungen gleich sind** oder zumindest die gleichen Parameter haben. Abhängig von der Verteilung müssen wir dafür unterschiedliche Tests verwenden. Wenn wir wissen, dass unsere Verteilungen normal sind, können wir den **[Student-t-Test](https://en.wikipedia.org/wiki/Student%27s_t-test)** anwenden.
Im Student-t-Test berechnen wir den sogenannten **t-Wert**, der den Unterschied zwischen den Mittelwerten unter Berücksichtigung der Varianz angibt. Es wird gezeigt, dass der t-Wert der **Student-Verteilung** folgt, was es uns ermöglicht, den Schwellenwert für ein gegebenes Konfidenzniveau **p** zu erhalten (dies kann berechnet oder in numerischen Tabellen nachgeschlagen werden). Wir vergleichen dann den t-Wert mit diesem Schwellenwert, um die Hypothese zu bestätigen oder abzulehnen.
In Python können wir das **SciPy**-Paket verwenden, das die Funktion `ttest_ind` enthält (zusätzlich zu vielen anderen nützlichen statistischen Funktionen!). Es berechnet den t-Wert für uns und führt auch die Rückwärtssuche des Konfidenz-p-Werts durch, sodass wir nur auf die Konfidenz schauen müssen, um eine Schlussfolgerung zu ziehen.
Zum Beispiel ergibt unser Vergleich zwischen den Größen der First und Second Basemen die folgenden Ergebnisse:
```python
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
```
```
T-value = 7.65
P-value: 9.137321189738925e-12
```
In unserem Fall ist der p-Wert sehr niedrig, was bedeutet, dass es starke Beweise dafür gibt, dass First Basemen größer sind.
Es gibt auch verschiedene andere Arten von Hypothesen, die wir testen könnten, zum Beispiel:
* Um zu beweisen, dass eine gegebene Stichprobe einer bestimmten Verteilung folgt. In unserem Fall haben wir angenommen, dass die Größen normal verteilt sind, aber das erfordert eine formale statistische Überprüfung.
* Um zu beweisen, dass der Mittelwert einer Stichprobe einem vordefinierten Wert entspricht.
* Um die Mittelwerte einer Anzahl von Stichproben zu vergleichen (z. B. den Unterschied in den Glücksniveaus zwischen verschiedenen Altersgruppen).
## Gesetz der großen Zahlen und zentraler Grenzwertsatz
Einer der Gründe, warum die Normalverteilung so wichtig ist, ist der sogenannte **zentrale Grenzwertsatz**. Angenommen, wir haben eine große Stichprobe von unabhängigen N Werten X1, ..., XN, die aus einer beliebigen Verteilung mit Mittelwert μ und Varianz σ2 entnommen wurden. Dann, für ausreichend großes N (mit anderen Worten, wenn N→∞), wird der Mittelwert ΣiXi normal verteilt sein, mit Mittelwert μ und Varianz σ2/N.
> Eine andere Möglichkeit, den zentralen Grenzwertsatz zu interpretieren, besteht darin zu sagen, dass unabhängig von der Verteilung, wenn Sie den Mittelwert einer Summe beliebiger Zufallsvariablen berechnen, Sie am Ende eine Normalverteilung erhalten.
Aus dem zentralen Grenzwertsatz folgt auch, dass, wenn N→∞, die Wahrscheinlichkeit, dass der Stichprobenmittelwert gleich μ ist, 1 wird. Dies ist als **Gesetz der großen Zahlen** bekannt.
## Kovarianz und Korrelation
Eine der Aufgaben der Datenwissenschaft besteht darin, Beziehungen zwischen Daten zu finden. Wir sagen, dass zwei Sequenzen **korrelieren**, wenn sie sich zur gleichen Zeit ähnlich verhalten, d.h. sie steigen/fallen gleichzeitig, oder eine Sequenz steigt, wenn die andere fällt und umgekehrt. Mit anderen Worten, es scheint eine Beziehung zwischen zwei Sequenzen zu geben.
> Korrelation zeigt nicht unbedingt eine kausale Beziehung zwischen zwei Sequenzen an; manchmal können beide Variablen von einer externen Ursache abhängen, oder es kann rein zufällig sein, dass die beiden Sequenzen korrelieren. Eine starke mathematische Korrelation ist jedoch ein guter Hinweis darauf, dass zwei Variablen irgendwie miteinander verbunden sind.
Mathematisch ist das Hauptkonzept, das die Beziehung zwischen zwei Zufallsvariablen zeigt, die **Kovarianz**, die wie folgt berechnet wird: Cov(X,Y) = **E**\[(X-**E**(X))(Y-**E**(Y))\]. Wir berechnen die Abweichung beider Variablen von ihren Mittelwerten und dann das Produkt dieser Abweichungen. Wenn beide Variablen zusammen abweichen, ist das Produkt immer ein positiver Wert, der zu einer positiven Kovarianz addiert wird. Wenn beide Variablen nicht synchron abweichen (d.h. eine fällt unter den Durchschnitt, wenn die andere über den Durchschnitt steigt), erhalten wir immer negative Zahlen, die zu einer negativen Kovarianz addiert werden. Wenn die Abweichungen unabhängig sind, summieren sie sich ungefähr zu null.
Der absolute Wert der Kovarianz sagt uns nicht viel darüber, wie groß die Korrelation ist, da er von der Größe der tatsächlichen Werte abhängt. Um sie zu normalisieren, können wir die Kovarianz durch die Standardabweichung beider Variablen teilen, um die **Korrelation** zu erhalten. Das Gute daran ist, dass die Korrelation immer im Bereich von [-1,1] liegt, wobei 1 eine starke positive Korrelation zwischen Werten anzeigt, -1 eine starke negative Korrelation und 0 keine Korrelation (Variablen sind unabhängig).
**Beispiel**: Wir können die Korrelation zwischen Gewichten und Größen von Baseballspielern aus dem oben genannten Datensatz berechnen:
```python
print(np.corrcoef(weights,heights))
```
Als Ergebnis erhalten wir eine **Korrelationsmatrix** wie diese:
```
array([[1. , 0.52959196],
[0.52959196, 1. ]])
```
> Die Korrelationsmatrix C kann für jede Anzahl von Eingabesequenzen S1, ..., Sn berechnet werden. Der Wert von Cij ist die Korrelation zwischen Si und Sj, und die Diagonalelemente sind immer 1 (was auch die Selbstkorrelation von Si ist).
In unserem Fall zeigt der Wert 0.53 an, dass es eine gewisse Korrelation zwischen dem Gewicht und der Größe einer Person gibt. Wir können auch das Streudiagramm eines Wertes gegen den anderen erstellen, um die Beziehung visuell zu sehen:

> Weitere Beispiele für Korrelation und Kovarianz finden Sie im [begleitenden Notebook](notebook.ipynb).
## Fazit
In diesem Abschnitt haben wir gelernt:
* grundlegende statistische Eigenschaften von Daten, wie Mittelwert, Varianz, Modus und Quartile
* verschiedene Verteilungen von Zufallsvariablen, einschließlich der Normalverteilung
* wie man Korrelationen zwischen verschiedenen Eigenschaften findet
* wie man mathematische und statistische Methoden verwendet, um Hypothesen zu beweisen
* wie man Konfidenzintervalle für Zufallsvariablen basierend auf Stichprobendaten berechnet
Obwohl dies definitiv keine vollständige Liste der Themen ist, die innerhalb der Wahrscheinlichkeit und Statistik existieren, sollte es ausreichen, um Ihnen einen guten Einstieg in diesen Kurs zu geben.
## 🚀 Herausforderung
Verwenden Sie den Beispielcode im Notebook, um andere Hypothesen zu testen:
1. First Basemen sind älter als Second Basemen
2. First Basemen sind größer als Third Basemen
3. Shortstops sind größer als Second Basemen
## [Quiz nach der Vorlesung](https://ff-quizzes.netlify.app/en/ds/quiz/7)
## Überprüfung & Selbststudium
Wahrscheinlichkeit und Statistik ist ein so breites Thema, dass es einen eigenen Kurs verdient. Wenn Sie tiefer in die Theorie eintauchen möchten, können Sie einige der folgenden Bücher lesen:
1. [Carlos Fernandez-Granda](https://cims.nyu.edu/~cfgranda/) von der New York University hat großartige Vorlesungsnotizen [Probability and Statistics for Data Science](https://cims.nyu.edu/~cfgranda/pages/stuff/probability_stats_for_DS.pdf) (online verfügbar)
1. [Peter und Andrew Bruce. Practical Statistics for Data Scientists.](https://www.oreilly.com/library/view/practical-statistics-for/9781491952955/) [[Beispielcode in R](https://github.com/andrewgbruce/statistics-for-data-scientists)].
1. [James D. Miller. Statistics for Data Science](https://www.packtpub.com/product/statistics-for-data-science/9781788290678) [[Beispielcode in R](https://github.com/PacktPublishing/Statistics-for-Data-Science)]
## Aufgabe
[Kleine Diabetes-Studie](assignment.md)
## Credits
Diese Lektion wurde mit ♥️ von [Dmitry Soshnikov](http://soshnikov.com) erstellt.
---
**Haftungsausschluss**:
Dieses Dokument wurde mithilfe des KI-Übersetzungsdienstes [Co-op Translator](https://github.com/Azure/co-op-translator) übersetzt. Obwohl wir uns um Genauigkeit bemühen, weisen wir darauf hin, dass automatisierte Übersetzungen Fehler oder Ungenauigkeiten enthalten können. Das Originaldokument in seiner ursprünglichen Sprache sollte als maßgebliche Quelle betrachtet werden. Für kritische Informationen wird eine professionelle menschliche Übersetzung empfohlen. Wir übernehmen keine Haftung für Missverständnisse oder Fehlinterpretationen, die aus der Nutzung dieser Übersetzung entstehen.
Hier berechnen wir auch den **Interquartilsabstand** IQR=Q3-Q1 und sogenannte **Ausreißer** – Werte, die außerhalb der Grenzen [Q1-1.5*IQR, Q3+1.5*IQR] liegen.
Für eine endliche Verteilung, die nur eine kleine Anzahl möglicher Werte enthält, ist ein guter "typischer" Wert derjenige, der am häufigsten vorkommt, der sogenannte **Modus**. Er wird oft auf kategoriale Daten angewendet, wie z. B. Farben. Betrachten Sie eine Situation, in der wir zwei Gruppen von Menschen haben – einige, die stark Rot bevorzugen, und andere, die Blau bevorzugen. Wenn wir Farben durch Zahlen kodieren, würde der Mittelwert für die Lieblingsfarbe irgendwo im orange-grünen Spektrum liegen, was die tatsächliche Präferenz keiner der Gruppen widerspiegelt. Der Modus hingegen wäre entweder eine der Farben oder beide Farben, wenn die Anzahl der Personen, die für sie stimmen, gleich ist (in diesem Fall nennen wir die Stichprobe **multimodal**).
## Reale Daten
Wenn wir Daten aus der realen Welt analysieren, sind sie oft keine Zufallsvariablen im eigentlichen Sinne, da wir keine Experimente mit unbekanntem Ergebnis durchführen. Betrachten Sie zum Beispiel ein Team von Baseballspielern und deren Körperdaten wie Größe, Gewicht und Alter. Diese Zahlen sind nicht wirklich zufällig, aber wir können dennoch dieselben mathematischen Konzepte anwenden. Zum Beispiel kann eine Sequenz von Gewichten von Personen als eine Sequenz von Werten betrachtet werden, die aus einer Zufallsvariablen gezogen wurden. Unten sehen Sie die Gewichtssequenz tatsächlicher Baseballspieler aus der [Major League Baseball](http://mlb.mlb.com/index.jsp), entnommen aus [diesem Datensatz](http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_MLB_HeightsWeights) (der Übersicht halber sind nur die ersten 20 Werte dargestellt):
```
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
```
> **Hinweis**: Um ein Beispiel für die Arbeit mit diesem Datensatz zu sehen, werfen Sie einen Blick auf das [begleitende Notebook](notebook.ipynb). Es gibt auch eine Reihe von Herausforderungen in dieser Lektion, die Sie durch das Hinzufügen von Code zu diesem Notebook abschließen können. Wenn Sie nicht sicher sind, wie man mit Daten arbeitet, machen Sie sich keine Sorgen – wir werden später darauf zurückkommen, wie man mit Python arbeitet. Wenn Sie nicht wissen, wie man Code in einem Jupyter Notebook ausführt, lesen Sie [diesen Artikel](https://soshnikov.com/education/how-to-execute-notebooks-from-github/).
Hier ist der Boxplot, der Mittelwert, Median und Quartile für unsere Daten zeigt:

Da unsere Daten Informationen über verschiedene Spieler**rollen** enthalten, können wir auch den Boxplot nach Rollen erstellen – so können wir erkennen, wie sich die Parameterwerte je nach Rolle unterscheiden. Diesmal betrachten wir die Größe:

Dieses Diagramm deutet darauf hin, dass die Größe von First Basemen im Durchschnitt höher ist als die von Second Basemen. Später in dieser Lektion werden wir lernen, wie wir diese Hypothese formeller testen können und wie wir zeigen können, dass unsere Daten statistisch signifikant sind, um dies zu belegen.
> Wenn wir mit realen Daten arbeiten, gehen wir davon aus, dass alle Datenpunkte Stichproben sind, die aus einer Wahrscheinlichkeitsverteilung gezogen wurden. Diese Annahme ermöglicht es uns, maschinelles Lernen anzuwenden und funktionierende Vorhersagemodelle zu erstellen.
Um zu sehen, wie die Verteilung unserer Daten aussieht, können wir ein Diagramm namens **Histogramm** erstellen. Die X-Achse enthält eine Anzahl verschiedener Gewichtsintervalle (sogenannte **Bins**), und die Y-Achse zeigt die Anzahl der Male, die unsere Zufallsvariablenstichprobe in ein bestimmtes Intervall fiel.

Aus diesem Histogramm können Sie erkennen, dass alle Werte um einen bestimmten mittleren Wert zentriert sind und dass die Wahrscheinlichkeit, dass ein Gewicht stark vom Mittelwert abweicht, geringer ist. Die Varianz der Gewichte zeigt, in welchem Maße die Gewichte wahrscheinlich vom Mittelwert abweichen.
> Wenn wir die Gewichte anderer Personen, die nicht aus der Baseballliga stammen, betrachten, ist die Verteilung wahrscheinlich anders. Die Form der Verteilung bleibt jedoch gleich, aber Mittelwert und Varianz ändern sich. Wenn wir unser Modell auf Baseballspieler trainieren, wird es wahrscheinlich falsche Ergebnisse liefern, wenn es auf Universitätsstudenten angewendet wird, da die zugrunde liegende Verteilung unterschiedlich ist.
## Normalverteilung
Die Verteilung der Gewichte, die wir oben gesehen haben, ist sehr typisch, und viele Messungen aus der realen Welt folgen demselben Verteilungstyp, jedoch mit unterschiedlichem Mittelwert und Varianz. Diese Verteilung wird als **Normalverteilung** bezeichnet und spielt eine sehr wichtige Rolle in der Statistik.
Die Verwendung der Normalverteilung ist eine korrekte Methode, um zufällige Gewichte potenzieller Baseballspieler zu generieren. Sobald wir den mittleren Wert `mean` und die Standardabweichung `std` kennen, können wir 1000 Gewichtsstichproben wie folgt generieren:
```python
samples = np.random.normal(mean,std,1000)
```
Wenn wir das Histogramm der generierten Stichproben zeichnen, sehen wir ein Bild, das dem oben gezeigten sehr ähnlich ist. Und wenn wir die Anzahl der Stichproben und die Anzahl der Bins erhöhen, können wir ein Bild einer Normalverteilung erzeugen, das näher an der idealen Form liegt:

*Normalverteilung mit Mittelwert=0 und Standardabweichung=1*
## Konfidenzintervalle
Wenn wir über die Gewichte von Baseballspielern sprechen, nehmen wir an, dass es eine bestimmte **Zufallsvariable W** gibt, die der idealen Wahrscheinlichkeitsverteilung der Gewichte aller Baseballspieler entspricht (sogenannte **Population**). Unsere Gewichtssequenz entspricht einer Teilmenge aller Baseballspieler, die wir als **Stichprobe** bezeichnen. Eine interessante Frage ist: Können wir die Parameter der Verteilung von W kennen, d. h. den Mittelwert und die Varianz der Population?
Die einfachste Antwort wäre, den Mittelwert und die Varianz unserer Stichprobe zu berechnen. Es könnte jedoch sein, dass unsere zufällige Stichprobe die gesamte Population nicht genau repräsentiert. Daher macht es Sinn, über **Konfidenzintervalle** zu sprechen.
> **Konfidenzintervall** ist die Schätzung des tatsächlichen Mittelwerts der Population basierend auf unserer Stichprobe, die mit einer bestimmten Wahrscheinlichkeit (oder **Konfidenzniveau**) korrekt ist.
Angenommen, wir haben eine Stichprobe X...
1, ..., Xn aus unserer Verteilung. Jedes Mal, wenn wir eine Stichprobe aus unserer Verteilung ziehen, erhalten wir einen anderen Mittelwert μ. Daher kann μ als Zufallsvariable betrachtet werden. Ein **Konfidenzintervall** mit Konfidenz p ist ein Wertepaar (Lp,Rp), sodass **P**(Lp≤μ≤Rp) = p, d.h. die Wahrscheinlichkeit, dass der gemessene Mittelwert innerhalb des Intervalls liegt, entspricht p.
Es geht über unsere kurze Einführung hinaus, im Detail zu erklären, wie diese Konfidenzintervalle berechnet werden. Weitere Details finden Sie [auf Wikipedia](https://en.wikipedia.org/wiki/Confidence_interval). Kurz gesagt, wir definieren die Verteilung des berechneten Stichprobenmittelwerts relativ zum wahren Mittelwert der Population, die als **Student-Verteilung** bezeichnet wird.
> **Interessante Tatsache**: Die Student-Verteilung ist nach dem Mathematiker William Sealy Gosset benannt, der seine Arbeit unter dem Pseudonym "Student" veröffentlichte. Er arbeitete in der Guinness-Brauerei, und laut einer Version wollte sein Arbeitgeber nicht, dass die Öffentlichkeit erfährt, dass sie statistische Tests zur Bestimmung der Qualität der Rohstoffe verwendeten.
Wenn wir den Mittelwert μ unserer Population mit Konfidenz p schätzen möchten, müssen wir das *(1-p)/2-te Perzentil* einer Student-Verteilung A nehmen, das entweder aus Tabellen entnommen oder mithilfe eingebauter Funktionen statistischer Software (z. B. Python, R usw.) berechnet werden kann. Dann wird das Intervall für μ durch X±A*D/√n gegeben, wobei X der erhaltene Mittelwert der Stichprobe und D die Standardabweichung ist.
> **Hinweis**: Wir lassen auch die Diskussion über ein wichtiges Konzept der [Freiheitsgrade](https://en.wikipedia.org/wiki/Degrees_of_freedom_(statistics)) aus, das im Zusammenhang mit der Student-Verteilung wichtig ist. Sie können auf umfassendere Bücher über Statistik zurückgreifen, um dieses Konzept tiefer zu verstehen.
Ein Beispiel für die Berechnung des Konfidenzintervalls für Gewichte und Größen finden Sie in den [begleitenden Notebooks](notebook.ipynb).
| p | Gewichtsmittelwert |
|-----|------------------|
| 0.85 | 201.73±0.94 |
| 0.90 | 201.73±1.08 |
| 0.95 | 201.73±1.28 |
Beachten Sie, dass je höher die Konfidenzwahrscheinlichkeit ist, desto breiter ist das Konfidenzintervall.
## Hypothesentests
In unserem Datensatz der Baseballspieler gibt es verschiedene Spielerrollen, die wie folgt zusammengefasst werden können (sehen Sie sich das [begleitende Notebook](notebook.ipynb) an, um zu sehen, wie diese Tabelle berechnet werden kann):
| Rolle | Größe | Gewicht | Anzahl |
|-------|-------|---------|--------|
| Catcher | 72.723684 | 204.328947 | 76 |
| Designated_Hitter | 74.222222 | 220.888889 | 18 |
| First_Baseman | 74.000000 | 213.109091 | 55 |
| Outfielder | 73.010309 | 199.113402 | 194 |
| Relief_Pitcher | 74.374603 | 203.517460 | 315 |
| Second_Baseman | 71.362069 | 184.344828 | 58 |
| Shortstop | 71.903846 | 182.923077 | 52 |
| Starting_Pitcher | 74.719457 | 205.163636 | 221 |
| Third_Baseman | 73.044444 | 200.955556 | 45 |
Wir können feststellen, dass die durchschnittliche Größe der First Basemen höher ist als die der Second Basemen. Daher könnten wir versucht sein, zu folgern, dass **First Basemen größer sind als Second Basemen**.
> Diese Aussage wird als **Hypothese** bezeichnet, da wir nicht wissen, ob die Tatsache tatsächlich wahr ist oder nicht.
Es ist jedoch nicht immer offensichtlich, ob wir diese Schlussfolgerung ziehen können. Aus der obigen Diskussion wissen wir, dass jeder Mittelwert ein zugehöriges Konfidenzintervall hat, und daher könnte dieser Unterschied nur ein statistischer Fehler sein. Wir benötigen eine formellere Methode, um unsere Hypothese zu testen.
Lassen Sie uns die Konfidenzintervalle separat für die Größen der First und Second Basemen berechnen:
| Konfidenz | First Basemen | Second Basemen |
|-----------|---------------|----------------|
| 0.85 | 73.62..74.38 | 71.04..71.69 |
| 0.90 | 73.56..74.44 | 70.99..71.73 |
| 0.95 | 73.47..74.53 | 70.92..71.81 |
Wir können sehen, dass die Intervalle unter keiner Konfidenz überlappen. Das beweist unsere Hypothese, dass First Basemen größer sind als Second Basemen.
Formeller gesagt, das Problem, das wir lösen, besteht darin zu prüfen, ob **zwei Wahrscheinlichkeitsverteilungen gleich sind** oder zumindest die gleichen Parameter haben. Abhängig von der Verteilung müssen wir dafür unterschiedliche Tests verwenden. Wenn wir wissen, dass unsere Verteilungen normal sind, können wir den **[Student-t-Test](https://en.wikipedia.org/wiki/Student%27s_t-test)** anwenden.
Im Student-t-Test berechnen wir den sogenannten **t-Wert**, der den Unterschied zwischen den Mittelwerten unter Berücksichtigung der Varianz angibt. Es wird gezeigt, dass der t-Wert der **Student-Verteilung** folgt, was es uns ermöglicht, den Schwellenwert für ein gegebenes Konfidenzniveau **p** zu erhalten (dies kann berechnet oder in numerischen Tabellen nachgeschlagen werden). Wir vergleichen dann den t-Wert mit diesem Schwellenwert, um die Hypothese zu bestätigen oder abzulehnen.
In Python können wir das **SciPy**-Paket verwenden, das die Funktion `ttest_ind` enthält (zusätzlich zu vielen anderen nützlichen statistischen Funktionen!). Es berechnet den t-Wert für uns und führt auch die Rückwärtssuche des Konfidenz-p-Werts durch, sodass wir nur auf die Konfidenz schauen müssen, um eine Schlussfolgerung zu ziehen.
Zum Beispiel ergibt unser Vergleich zwischen den Größen der First und Second Basemen die folgenden Ergebnisse:
```python
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
```
```
T-value = 7.65
P-value: 9.137321189738925e-12
```
In unserem Fall ist der p-Wert sehr niedrig, was bedeutet, dass es starke Beweise dafür gibt, dass First Basemen größer sind.
Es gibt auch verschiedene andere Arten von Hypothesen, die wir testen könnten, zum Beispiel:
* Um zu beweisen, dass eine gegebene Stichprobe einer bestimmten Verteilung folgt. In unserem Fall haben wir angenommen, dass die Größen normal verteilt sind, aber das erfordert eine formale statistische Überprüfung.
* Um zu beweisen, dass der Mittelwert einer Stichprobe einem vordefinierten Wert entspricht.
* Um die Mittelwerte einer Anzahl von Stichproben zu vergleichen (z. B. den Unterschied in den Glücksniveaus zwischen verschiedenen Altersgruppen).
## Gesetz der großen Zahlen und zentraler Grenzwertsatz
Einer der Gründe, warum die Normalverteilung so wichtig ist, ist der sogenannte **zentrale Grenzwertsatz**. Angenommen, wir haben eine große Stichprobe von unabhängigen N Werten X1, ..., XN, die aus einer beliebigen Verteilung mit Mittelwert μ und Varianz σ2 entnommen wurden. Dann, für ausreichend großes N (mit anderen Worten, wenn N→∞), wird der Mittelwert ΣiXi normal verteilt sein, mit Mittelwert μ und Varianz σ2/N.
> Eine andere Möglichkeit, den zentralen Grenzwertsatz zu interpretieren, besteht darin zu sagen, dass unabhängig von der Verteilung, wenn Sie den Mittelwert einer Summe beliebiger Zufallsvariablen berechnen, Sie am Ende eine Normalverteilung erhalten.
Aus dem zentralen Grenzwertsatz folgt auch, dass, wenn N→∞, die Wahrscheinlichkeit, dass der Stichprobenmittelwert gleich μ ist, 1 wird. Dies ist als **Gesetz der großen Zahlen** bekannt.
## Kovarianz und Korrelation
Eine der Aufgaben der Datenwissenschaft besteht darin, Beziehungen zwischen Daten zu finden. Wir sagen, dass zwei Sequenzen **korrelieren**, wenn sie sich zur gleichen Zeit ähnlich verhalten, d.h. sie steigen/fallen gleichzeitig, oder eine Sequenz steigt, wenn die andere fällt und umgekehrt. Mit anderen Worten, es scheint eine Beziehung zwischen zwei Sequenzen zu geben.
> Korrelation zeigt nicht unbedingt eine kausale Beziehung zwischen zwei Sequenzen an; manchmal können beide Variablen von einer externen Ursache abhängen, oder es kann rein zufällig sein, dass die beiden Sequenzen korrelieren. Eine starke mathematische Korrelation ist jedoch ein guter Hinweis darauf, dass zwei Variablen irgendwie miteinander verbunden sind.
Mathematisch ist das Hauptkonzept, das die Beziehung zwischen zwei Zufallsvariablen zeigt, die **Kovarianz**, die wie folgt berechnet wird: Cov(X,Y) = **E**\[(X-**E**(X))(Y-**E**(Y))\]. Wir berechnen die Abweichung beider Variablen von ihren Mittelwerten und dann das Produkt dieser Abweichungen. Wenn beide Variablen zusammen abweichen, ist das Produkt immer ein positiver Wert, der zu einer positiven Kovarianz addiert wird. Wenn beide Variablen nicht synchron abweichen (d.h. eine fällt unter den Durchschnitt, wenn die andere über den Durchschnitt steigt), erhalten wir immer negative Zahlen, die zu einer negativen Kovarianz addiert werden. Wenn die Abweichungen unabhängig sind, summieren sie sich ungefähr zu null.
Der absolute Wert der Kovarianz sagt uns nicht viel darüber, wie groß die Korrelation ist, da er von der Größe der tatsächlichen Werte abhängt. Um sie zu normalisieren, können wir die Kovarianz durch die Standardabweichung beider Variablen teilen, um die **Korrelation** zu erhalten. Das Gute daran ist, dass die Korrelation immer im Bereich von [-1,1] liegt, wobei 1 eine starke positive Korrelation zwischen Werten anzeigt, -1 eine starke negative Korrelation und 0 keine Korrelation (Variablen sind unabhängig).
**Beispiel**: Wir können die Korrelation zwischen Gewichten und Größen von Baseballspielern aus dem oben genannten Datensatz berechnen:
```python
print(np.corrcoef(weights,heights))
```
Als Ergebnis erhalten wir eine **Korrelationsmatrix** wie diese:
```
array([[1. , 0.52959196],
[0.52959196, 1. ]])
```
> Die Korrelationsmatrix C kann für jede Anzahl von Eingabesequenzen S1, ..., Sn berechnet werden. Der Wert von Cij ist die Korrelation zwischen Si und Sj, und die Diagonalelemente sind immer 1 (was auch die Selbstkorrelation von Si ist).
In unserem Fall zeigt der Wert 0.53 an, dass es eine gewisse Korrelation zwischen dem Gewicht und der Größe einer Person gibt. Wir können auch das Streudiagramm eines Wertes gegen den anderen erstellen, um die Beziehung visuell zu sehen:

> Weitere Beispiele für Korrelation und Kovarianz finden Sie im [begleitenden Notebook](notebook.ipynb).
## Fazit
In diesem Abschnitt haben wir gelernt:
* grundlegende statistische Eigenschaften von Daten, wie Mittelwert, Varianz, Modus und Quartile
* verschiedene Verteilungen von Zufallsvariablen, einschließlich der Normalverteilung
* wie man Korrelationen zwischen verschiedenen Eigenschaften findet
* wie man mathematische und statistische Methoden verwendet, um Hypothesen zu beweisen
* wie man Konfidenzintervalle für Zufallsvariablen basierend auf Stichprobendaten berechnet
Obwohl dies definitiv keine vollständige Liste der Themen ist, die innerhalb der Wahrscheinlichkeit und Statistik existieren, sollte es ausreichen, um Ihnen einen guten Einstieg in diesen Kurs zu geben.
## 🚀 Herausforderung
Verwenden Sie den Beispielcode im Notebook, um andere Hypothesen zu testen:
1. First Basemen sind älter als Second Basemen
2. First Basemen sind größer als Third Basemen
3. Shortstops sind größer als Second Basemen
## [Quiz nach der Vorlesung](https://ff-quizzes.netlify.app/en/ds/quiz/7)
## Überprüfung & Selbststudium
Wahrscheinlichkeit und Statistik ist ein so breites Thema, dass es einen eigenen Kurs verdient. Wenn Sie tiefer in die Theorie eintauchen möchten, können Sie einige der folgenden Bücher lesen:
1. [Carlos Fernandez-Granda](https://cims.nyu.edu/~cfgranda/) von der New York University hat großartige Vorlesungsnotizen [Probability and Statistics for Data Science](https://cims.nyu.edu/~cfgranda/pages/stuff/probability_stats_for_DS.pdf) (online verfügbar)
1. [Peter und Andrew Bruce. Practical Statistics for Data Scientists.](https://www.oreilly.com/library/view/practical-statistics-for/9781491952955/) [[Beispielcode in R](https://github.com/andrewgbruce/statistics-for-data-scientists)].
1. [James D. Miller. Statistics for Data Science](https://www.packtpub.com/product/statistics-for-data-science/9781788290678) [[Beispielcode in R](https://github.com/PacktPublishing/Statistics-for-Data-Science)]
## Aufgabe
[Kleine Diabetes-Studie](assignment.md)
## Credits
Diese Lektion wurde mit ♥️ von [Dmitry Soshnikov](http://soshnikov.com) erstellt.
---
**Haftungsausschluss**:
Dieses Dokument wurde mithilfe des KI-Übersetzungsdienstes [Co-op Translator](https://github.com/Azure/co-op-translator) übersetzt. Obwohl wir uns um Genauigkeit bemühen, weisen wir darauf hin, dass automatisierte Übersetzungen Fehler oder Ungenauigkeiten enthalten können. Das Originaldokument in seiner ursprünglichen Sprache sollte als maßgebliche Quelle betrachtet werden. Für kritische Informationen wird eine professionelle menschliche Übersetzung empfohlen. Wir übernehmen keine Haftung für Missverständnisse oder Fehlinterpretationen, die aus der Nutzung dieser Übersetzung entstehen.