# 统计与概率简要介绍
| ](../../sketchnotes/04-Statistics-Probability.png)|
|:---:|
| 统计与概率 - _由 [@nitya](https://twitter.com/nitya) 绘制的速记图_ |
统计学和概率论是数学中两个密切相关的领域,与数据科学息息相关。虽然可以在不了解深奥数学知识的情况下处理数据,但至少掌握一些基本概念会更好。这里我们将提供一个简短的介绍,帮助你入门。
[](https://youtu.be/Z5Zy85g4Yjw)
## [课前测验](https://purple-hill-04aebfb03.1.azurestaticapps.net/quiz/6)
## 概率与随机变量
**概率**是一个介于 0 和 1 之间的数字,用来表示某个**事件**发生的可能性。它定义为正结果(导致事件发生的结果)的数量除以总结果数量,前提是所有结果的可能性相等。例如,当我们掷骰子时,得到偶数的概率是 3/6 = 0.5。
谈到事件时,我们会使用**随机变量**。例如,表示掷骰子结果的随机变量会取值 1 到 6。1 到 6 的集合称为**样本空间**。我们可以讨论随机变量取某个值的概率,例如 P(X=3)=1/6。
上述例子中的随机变量称为**离散型**,因为它有一个可计数的样本空间,即可以枚举的独立值。有些情况下,样本空间是实数范围或整个实数集。这类变量称为**连续型**。一个典型的例子是公交车到达的时间。
## 概率分布
对于离散随机变量,可以通过函数 P(X)轻松描述每个事件的概率。对于样本空间 *S* 中的每个值 *s*,它会给出一个介于 0 和 1 之间的数字,并且所有事件的 P(X=s) 值的总和为 1。
最著名的离散分布是**均匀分布**,其中样本空间有 N 个元素,每个元素的概率均为 1/N。
描述连续变量的概率分布则更复杂,这些变量的值可能来自某个区间 [a,b] 或整个实数集 ℝ。以公交车到达时间为例。实际上,对于每个确切的到达时间 *t*,公交车恰好在该时间到达的概率是 0!
> 现在你知道了概率为 0 的事件是会发生的,而且非常频繁!至少每次公交车到达时都是如此!
我们只能讨论变量落入某个值区间的概率,例如 P(t1≤X2)。在这种情况下,概率分布由**概率密度函数** p(x) 描述,其满足:
 这里我们还计算了**四分位距** IQR=Q3-Q1,以及所谓的**离群值**——位于区间 [Q1-1.5*IQR,Q3+1.5*IQR] 之外的值。
对于包含少量可能值的有限分布,一个良好的“典型”值是出现频率最高的值,称为**众数**。众数通常应用于分类数据,例如颜色。考虑一种情况,我们有两组人——一组强烈偏爱红色,另一组偏爱蓝色。如果我们用数字编码颜色,最喜欢的颜色的均值可能会落在橙色或绿色范围,这无法反映任何一组的实际偏好。然而,众数可能是其中一种颜色,或者两种颜色(如果投票人数相等,在这种情况下称为**多众分布**)。
## 真实世界数据
当我们分析现实生活中的数据时,它们通常不是严格意义上的随机变量,因为我们并未进行未知结果的实验。例如,考虑一组棒球运动员及其身体数据,如身高、体重和年龄。这些数字并不完全随机,但我们仍然可以应用相同的数学概念。例如,一组人的体重可以被视为从某个随机变量中抽取的一组值。以下是来自 [美国职业棒球大联盟](http://mlb.mlb.com/index.jsp) 的实际棒球运动员体重序列(数据来源于 [此数据集](http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_MLB_HeightsWeights),为方便起见,仅显示前 20 个值):
```
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
```
> **注意**:要查看使用此数据集的示例,请参阅[配套笔记本](../../../../1-Introduction/04-stats-and-probability/notebook.ipynb)。本课程中还有许多挑战,你可以通过向该笔记本添加代码来完成它们。如果你不确定如何操作数据,不必担心——我们稍后会回到使用 Python 处理数据的部分。如果你不知道如何在 Jupyter Notebook 中运行代码,请查看[这篇文章](https://soshnikov.com/education/how-to-execute-notebooks-from-github/)。
以下是显示我们数据均值、中位数和四分位数的箱形图:
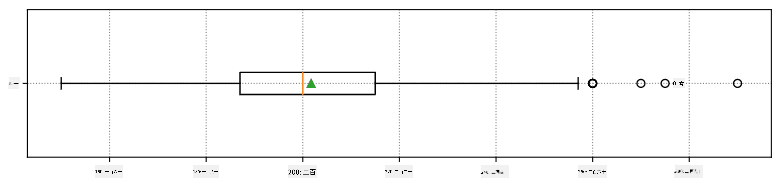
由于我们的数据包含不同球员**角色**的信息,我们还可以按角色绘制箱形图——这将帮助我们了解参数值在不同角色之间的差异。这次我们考虑身高:
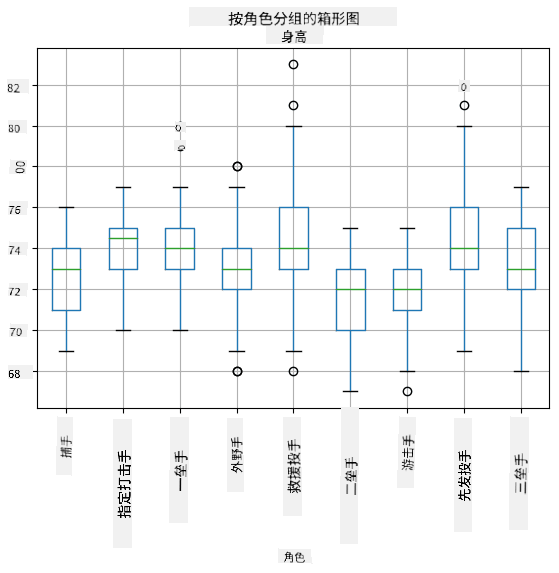
该图表表明,平均而言,一垒手的身高高于二垒手的身高。在本课程后面,我们将学习如何更正式地验证这一假设,以及如何证明我们的数据在统计上具有显著性。
> 在处理真实世界数据时,我们假设所有数据点是从某个概率分布中抽取的样本。这个假设使我们能够应用机器学习技术并构建有效的预测模型。
为了查看数据的分布,我们可以绘制一个称为**直方图**的图表。X 轴包含多个不同的体重区间(即所谓的**分箱**),Y 轴显示随机变量样本落入某个区间的次数。
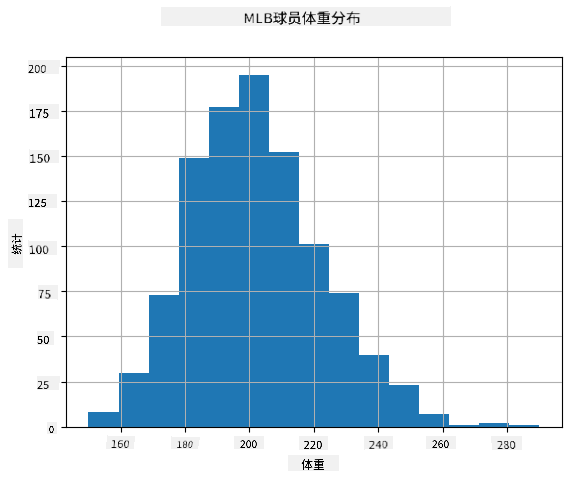
从这个直方图可以看出,所有值都集中在某个平均体重附近,离平均体重越远,出现该体重值的次数越少。也就是说,棒球运动员的体重与平均体重差异很大的可能性非常小。体重的方差显示了体重值与平均值可能的差异程度。
> 如果我们取其他人群的体重数据,而不是棒球联盟的球员,分布可能会有所不同。然而,分布的形状会保持一致,但均值和方差会发生变化。因此,如果我们在棒球运动员上训练模型,当应用于大学学生时可能会产生错误结果,因为底层分布不同。
## 正态分布
我们上面看到的体重分布非常典型,许多现实世界的测量值遵循相同类型的分布,但均值和方差不同。这种分布称为**正态分布**,在统计学中具有非常重要的作用。
使用正态分布是生成潜在棒球运动员随机体重的正确方法。一旦我们知道平均体重 `mean` 和标准差 `std`,我们可以通过以下方式生成 1000 个体重样本:
```python
samples = np.random.normal(mean,std,1000)
```
如果我们绘制生成样本的直方图,会看到与上图非常相似的图像。如果我们增加样本数量和分箱数量,可以生成更接近理想的正态分布图像:
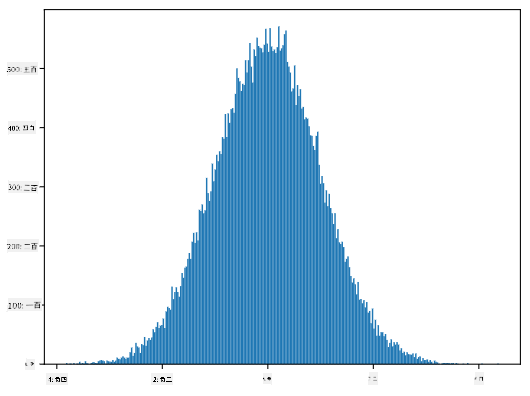
*均值=0,标准差=1 的正态分布*
## 置信区间
当我们讨论棒球运动员的体重时,我们假设存在某个**随机变量 W**,它对应于所有棒球运动员体重的理想概率分布(即所谓的**总体**)。我们的体重序列对应于所有棒球运动员的一个子集,称为**样本**。一个有趣的问题是,我们能否知道 W 的分布参数,即总体的均值和方差?
最简单的答案是计算样本的均值和方差。然而,可能出现我们的随机样本未能准确代表完整总体的情况。因此,谈论**置信区间**是有意义的。
> **置信区间** 是基于我们的样本对总体真实均值的估计,其准确性在某一概率(或 **置信水平**)范围内。
假设我们有一个样本 X1, ..., Xn 来自某个分布。每次从分布中抽取样本时,我们会得到不同的均值 μ。因此,μ 可以被视为一个随机变量。一个置信度为 p 的 **置信区间** 是一对值 (Lp,Rp),使得 **P**(Lp≤μ≤Rp) = p,即测得的均值落在该区间内的概率等于 p。
详细讨论如何计算这些置信区间超出了我们的简短介绍范围。更多细节可以参考 [维基百科](https://en.wikipedia.org/wiki/Confidence_interval)。简而言之,我们定义了相对于总体真实均值的样本均值分布,这被称为 **t 分布**。
> **有趣的事实**:t 分布的名称来源于数学家 William Sealy Gosset,他以笔名 "Student" 发表了相关论文。他当时在健力士啤酒厂工作,据说他的雇主不希望公众知道他们使用统计测试来评估原材料的质量。
如果我们希望以置信度 p 估计总体均值 μ,我们需要取 t 分布 A 的 *(1-p)/2 分位数*,这可以从表格中查得,或者通过统计软件(如 Python、R 等)的内置函数计算。然后,μ 的区间为 X±A*D/√n,其中 X 是样本的均值,D 是标准差。
> **注意**:我们还省略了与 t 分布相关的重要概念 [自由度](https://en.wikipedia.org/wiki/Degrees_of_freedom_(statistics)) 的讨论。您可以参考更完整的统计学书籍以深入理解这一概念。
关于体重和身高的置信区间计算示例可以在 [附带的笔记本](../../../../1-Introduction/04-stats-and-probability/notebook.ipynb) 中找到。
| p | 体重均值 |
|------|---------------|
| 0.85 | 201.73±0.94 |
| 0.90 | 201.73±1.08 |
| 0.95 | 201.73±1.28 |
注意,置信概率越高,置信区间越宽。
## 假设检验
在我们的棒球运动员数据集中,有不同的球员角色,可以总结如下(查看 [附带的笔记本](../../../../1-Introduction/04-stats-and-probability/notebook.ipynb) 了解如何计算此表):
| 角色 | 身高 | 体重 | 数量 |
|-------------------|-----------|-----------|-------|
| 捕手 | 72.723684 | 204.328947 | 76 |
| 指定打击手 | 74.222222 | 220.888889 | 18 |
| 一垒手 | 74.000000 | 213.109091 | 55 |
| 外野手 | 73.010309 | 199.113402 | 194 |
| 救援投手 | 74.374603 | 203.517460 | 315 |
| 二垒手 | 71.362069 | 184.344828 | 58 |
| 游击手 | 71.903846 | 182.923077 | 52 |
| 先发投手 | 74.719457 | 205.163636 | 221 |
| 三垒手 | 73.044444 | 200.955556 | 45 |
我们可以注意到,一垒手的平均身高高于二垒手。因此,我们可能会得出结论:**一垒手比二垒手高**。
> 这个陈述被称为 **假设**,因为我们并不知道这一事实是否真的成立。
然而,是否可以得出这一结论并不总是显而易见的。从上面的讨论中我们知道,每个均值都有一个相关的置信区间,因此这种差异可能只是统计误差。我们需要更正式的方法来检验我们的假设。
让我们分别计算一垒手和二垒手身高的置信区间:
| 置信度 | 一垒手 | 二垒手 |
|--------|---------------|---------------|
| 0.85 | 73.62..74.38 | 71.04..71.69 |
| 0.90 | 73.56..74.44 | 70.99..71.73 |
| 0.95 | 73.47..74.53 | 70.92..71.81 |
我们可以看到,在任何置信度下,这些区间都没有重叠。这证明了我们的假设:一垒手比二垒手高。
更正式地说,我们要解决的问题是判断 **两个概率分布是否相同**,或者至少它们的参数是否相同。根据分布的不同,我们需要使用不同的检验方法。如果我们知道分布是正态分布,我们可以应用 **[t 检验](https://en.wikipedia.org/wiki/Student%27s_t-test)**。
在 t 检验中,我们计算所谓的 **t 值**,它表示均值之间的差异,同时考虑方差。研究表明,t 值服从 **t 分布**,这使我们能够为给定的置信水平 **p** 获取阈值(可以通过计算或查表获得)。然后,我们将 t 值与该阈值进行比较,以接受或拒绝假设。
在 Python 中,我们可以使用 **SciPy** 包,其中包括 `ttest_ind` 函数(以及许多其他有用的统计函数!)。它为我们计算 t 值,并反向查找置信 p 值,这样我们只需查看置信度即可得出结论。
例如,我们比较一垒手和二垒手身高的结果如下:
```python
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
```
```
T-value = 7.65
P-value: 9.137321189738925e-12
```
在我们的例子中,p 值非常低,这意味着有强有力的证据支持一垒手更高的结论。
我们还可以测试其他类型的假设,例如:
* 证明某个样本符合某种分布。在我们的例子中,我们假设身高是正态分布的,但这需要正式的统计验证。
* 证明样本的均值与某个预定义值相符。
* 比较多个样本的均值(例如,不同年龄组的幸福感差异)。
## 大数法则和中心极限定理
正态分布如此重要的原因之一是所谓的 **中心极限定理**。假设我们有一个独立的 N 个值 X1, ..., XN 的大样本,这些值来自任何均值为 μ、方差为 σ2 的分布。那么,当 N 足够大时(换句话说,当 N→∞),均值 ΣiXi 将服从正态分布,均值为 μ,方差为 σ2/N。
> 中心极限定理的另一种解释是,无论分布如何,当你计算任意随机变量值的和的均值时,最终都会得到正态分布。
根据中心极限定理,当 N→∞ 时,样本均值等于 μ 的概率趋于 1。这被称为 **大数法则**。
## 协方差和相关性
数据科学的一个任务是发现数据之间的关系。当两个序列在同一时间表现出相似的行为时,我们称它们 **相关**,即它们要么同时上升/下降,要么一个序列上升时另一个下降,反之亦然。换句话说,这两个序列之间似乎存在某种关系。
> 相关性并不一定表明两个序列之间存在因果关系;有时两个变量可能依赖于某个外部原因,或者它们的相关性可能纯属偶然。然而,强烈的数学相关性是两个变量某种程度上相互关联的良好指示。
从数学上讲,显示两个随机变量之间关系的主要概念是 **协方差**,其计算公式为:Cov(X,Y) = **E**\[(X-**E**(X))(Y-**E**(Y))\]。我们计算两个变量相对于其均值的偏差,然后将这些偏差相乘。如果两个变量一起偏离,其乘积总是正值,最终得到正协方差。如果两个变量不同步偏离(即一个低于平均值时另一个高于平均值),我们总是得到负值,最终得到负协方差。如果偏差无关,它们的和大致为零。
协方差的绝对值并不能告诉我们相关性的强弱,因为它取决于实际值的大小。为了归一化,我们可以将协方差除以两个变量的标准差,得到 **相关性**。相关性的好处是它总是介于 [-1,1] 之间,其中 1 表示强正相关,-1 表示强负相关,0 表示完全无相关(变量独立)。
**示例**:我们可以计算棒球运动员体重和身高之间的相关性:
```python
print(np.corrcoef(weights,heights))
```
结果是一个 **相关性矩阵**,如下所示:
```
array([[1. , 0.52959196],
[0.52959196, 1. ]])
```
> 相关性矩阵 C 可以针对任意数量的输入序列 S1, ..., Sn 计算。Cij 的值是 Si 和 Sj 之间的相关性,对角线元素总是 1(即 Si 的自相关性)。
在我们的例子中,值 0.53 表明体重和身高之间存在一定的相关性。我们还可以绘制一个散点图,将一个值与另一个值进行比较,以直观地观察它们之间的关系:
> 更多关于相关性和协方差的示例可以在 [附带的笔记本](../../../../1-Introduction/04-stats-and-probability/notebook.ipynb) 中找到。
## 总结
在本节中,我们学习了:
* 数据的基本统计属性,如均值、方差、中位数和四分位数
* 随机变量的不同分布,包括正态分布
* 如何找到不同属性之间的相关性
* 如何使用数学和统计学的严谨工具来验证假设
* 如何根据数据样本计算随机变量的置信区间
虽然这绝不是概率和统计学中所有主题的详尽列表,但它应该足以为您进入本课程提供一个良好的起点。
## 🚀 挑战
使用笔记本中的示例代码测试以下假设:
1. 一垒手比二垒手年长
2. 一垒手比三垒手高
3. 游击手比二垒手高
## [课后测验](https://purple-hill-04aebfb03.1.azurestaticapps.net/quiz/7)
## 复习与自学
概率和统计学是一个非常广泛的主题,值得开设一门独立的课程。如果您有兴趣深入研究理论,可以继续阅读以下书籍:
1. [Carlos Fernandez-Granda](https://cims.nyu.edu/~cfgranda/) 来自纽约大学的优秀讲义 [Probability and Statistics for Data Science](https://cims.nyu.edu/~cfgranda/pages/stuff/probability_stats_for_DS.pdf)(在线可用)
2. [Peter and Andrew Bruce. Practical Statistics for Data Scientists.](https://www.oreilly.com/library/view/practical-statistics-for/9781491952955/) [[R 示例代码](https://github.com/andrewgbruce/statistics-for-data-scientists)]。
3. [James D. Miller. Statistics for Data Science](https://www.packtpub.com/product/statistics-for-data-science/9781788290678) [[R 示例代码](https://github.com/PacktPublishing/Statistics-for-Data-Science)]
## 作业
[小型糖尿病研究](assignment.md)
## 致谢
本课程由 [Dmitry Soshnikov](http://soshnikov.com) 倾情创作。
**免责声明**:
本文档使用AI翻译服务 [Co-op Translator](https://github.com/Azure/co-op-translator) 进行翻译。尽管我们努力确保翻译的准确性,但请注意,自动翻译可能包含错误或不准确之处。原始语言的文档应被视为权威来源。对于重要信息,建议使用专业人工翻译。我们不对因使用此翻译而产生的任何误解或误读承担责任。
这里我们还计算了**四分位距** IQR=Q3-Q1,以及所谓的**离群值**——位于区间 [Q1-1.5*IQR,Q3+1.5*IQR] 之外的值。
对于包含少量可能值的有限分布,一个良好的“典型”值是出现频率最高的值,称为**众数**。众数通常应用于分类数据,例如颜色。考虑一种情况,我们有两组人——一组强烈偏爱红色,另一组偏爱蓝色。如果我们用数字编码颜色,最喜欢的颜色的均值可能会落在橙色或绿色范围,这无法反映任何一组的实际偏好。然而,众数可能是其中一种颜色,或者两种颜色(如果投票人数相等,在这种情况下称为**多众分布**)。
## 真实世界数据
当我们分析现实生活中的数据时,它们通常不是严格意义上的随机变量,因为我们并未进行未知结果的实验。例如,考虑一组棒球运动员及其身体数据,如身高、体重和年龄。这些数字并不完全随机,但我们仍然可以应用相同的数学概念。例如,一组人的体重可以被视为从某个随机变量中抽取的一组值。以下是来自 [美国职业棒球大联盟](http://mlb.mlb.com/index.jsp) 的实际棒球运动员体重序列(数据来源于 [此数据集](http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_MLB_HeightsWeights),为方便起见,仅显示前 20 个值):
```
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
```
> **注意**:要查看使用此数据集的示例,请参阅[配套笔记本](../../../../1-Introduction/04-stats-and-probability/notebook.ipynb)。本课程中还有许多挑战,你可以通过向该笔记本添加代码来完成它们。如果你不确定如何操作数据,不必担心——我们稍后会回到使用 Python 处理数据的部分。如果你不知道如何在 Jupyter Notebook 中运行代码,请查看[这篇文章](https://soshnikov.com/education/how-to-execute-notebooks-from-github/)。
以下是显示我们数据均值、中位数和四分位数的箱形图:

由于我们的数据包含不同球员**角色**的信息,我们还可以按角色绘制箱形图——这将帮助我们了解参数值在不同角色之间的差异。这次我们考虑身高:

该图表表明,平均而言,一垒手的身高高于二垒手的身高。在本课程后面,我们将学习如何更正式地验证这一假设,以及如何证明我们的数据在统计上具有显著性。
> 在处理真实世界数据时,我们假设所有数据点是从某个概率分布中抽取的样本。这个假设使我们能够应用机器学习技术并构建有效的预测模型。
为了查看数据的分布,我们可以绘制一个称为**直方图**的图表。X 轴包含多个不同的体重区间(即所谓的**分箱**),Y 轴显示随机变量样本落入某个区间的次数。

从这个直方图可以看出,所有值都集中在某个平均体重附近,离平均体重越远,出现该体重值的次数越少。也就是说,棒球运动员的体重与平均体重差异很大的可能性非常小。体重的方差显示了体重值与平均值可能的差异程度。
> 如果我们取其他人群的体重数据,而不是棒球联盟的球员,分布可能会有所不同。然而,分布的形状会保持一致,但均值和方差会发生变化。因此,如果我们在棒球运动员上训练模型,当应用于大学学生时可能会产生错误结果,因为底层分布不同。
## 正态分布
我们上面看到的体重分布非常典型,许多现实世界的测量值遵循相同类型的分布,但均值和方差不同。这种分布称为**正态分布**,在统计学中具有非常重要的作用。
使用正态分布是生成潜在棒球运动员随机体重的正确方法。一旦我们知道平均体重 `mean` 和标准差 `std`,我们可以通过以下方式生成 1000 个体重样本:
```python
samples = np.random.normal(mean,std,1000)
```
如果我们绘制生成样本的直方图,会看到与上图非常相似的图像。如果我们增加样本数量和分箱数量,可以生成更接近理想的正态分布图像:

*均值=0,标准差=1 的正态分布*
## 置信区间
当我们讨论棒球运动员的体重时,我们假设存在某个**随机变量 W**,它对应于所有棒球运动员体重的理想概率分布(即所谓的**总体**)。我们的体重序列对应于所有棒球运动员的一个子集,称为**样本**。一个有趣的问题是,我们能否知道 W 的分布参数,即总体的均值和方差?
最简单的答案是计算样本的均值和方差。然而,可能出现我们的随机样本未能准确代表完整总体的情况。因此,谈论**置信区间**是有意义的。
> **置信区间** 是基于我们的样本对总体真实均值的估计,其准确性在某一概率(或 **置信水平**)范围内。
假设我们有一个样本 X1, ..., Xn 来自某个分布。每次从分布中抽取样本时,我们会得到不同的均值 μ。因此,μ 可以被视为一个随机变量。一个置信度为 p 的 **置信区间** 是一对值 (Lp,Rp),使得 **P**(Lp≤μ≤Rp) = p,即测得的均值落在该区间内的概率等于 p。
详细讨论如何计算这些置信区间超出了我们的简短介绍范围。更多细节可以参考 [维基百科](https://en.wikipedia.org/wiki/Confidence_interval)。简而言之,我们定义了相对于总体真实均值的样本均值分布,这被称为 **t 分布**。
> **有趣的事实**:t 分布的名称来源于数学家 William Sealy Gosset,他以笔名 "Student" 发表了相关论文。他当时在健力士啤酒厂工作,据说他的雇主不希望公众知道他们使用统计测试来评估原材料的质量。
如果我们希望以置信度 p 估计总体均值 μ,我们需要取 t 分布 A 的 *(1-p)/2 分位数*,这可以从表格中查得,或者通过统计软件(如 Python、R 等)的内置函数计算。然后,μ 的区间为 X±A*D/√n,其中 X 是样本的均值,D 是标准差。
> **注意**:我们还省略了与 t 分布相关的重要概念 [自由度](https://en.wikipedia.org/wiki/Degrees_of_freedom_(statistics)) 的讨论。您可以参考更完整的统计学书籍以深入理解这一概念。
关于体重和身高的置信区间计算示例可以在 [附带的笔记本](../../../../1-Introduction/04-stats-and-probability/notebook.ipynb) 中找到。
| p | 体重均值 |
|------|---------------|
| 0.85 | 201.73±0.94 |
| 0.90 | 201.73±1.08 |
| 0.95 | 201.73±1.28 |
注意,置信概率越高,置信区间越宽。
## 假设检验
在我们的棒球运动员数据集中,有不同的球员角色,可以总结如下(查看 [附带的笔记本](../../../../1-Introduction/04-stats-and-probability/notebook.ipynb) 了解如何计算此表):
| 角色 | 身高 | 体重 | 数量 |
|-------------------|-----------|-----------|-------|
| 捕手 | 72.723684 | 204.328947 | 76 |
| 指定打击手 | 74.222222 | 220.888889 | 18 |
| 一垒手 | 74.000000 | 213.109091 | 55 |
| 外野手 | 73.010309 | 199.113402 | 194 |
| 救援投手 | 74.374603 | 203.517460 | 315 |
| 二垒手 | 71.362069 | 184.344828 | 58 |
| 游击手 | 71.903846 | 182.923077 | 52 |
| 先发投手 | 74.719457 | 205.163636 | 221 |
| 三垒手 | 73.044444 | 200.955556 | 45 |
我们可以注意到,一垒手的平均身高高于二垒手。因此,我们可能会得出结论:**一垒手比二垒手高**。
> 这个陈述被称为 **假设**,因为我们并不知道这一事实是否真的成立。
然而,是否可以得出这一结论并不总是显而易见的。从上面的讨论中我们知道,每个均值都有一个相关的置信区间,因此这种差异可能只是统计误差。我们需要更正式的方法来检验我们的假设。
让我们分别计算一垒手和二垒手身高的置信区间:
| 置信度 | 一垒手 | 二垒手 |
|--------|---------------|---------------|
| 0.85 | 73.62..74.38 | 71.04..71.69 |
| 0.90 | 73.56..74.44 | 70.99..71.73 |
| 0.95 | 73.47..74.53 | 70.92..71.81 |
我们可以看到,在任何置信度下,这些区间都没有重叠。这证明了我们的假设:一垒手比二垒手高。
更正式地说,我们要解决的问题是判断 **两个概率分布是否相同**,或者至少它们的参数是否相同。根据分布的不同,我们需要使用不同的检验方法。如果我们知道分布是正态分布,我们可以应用 **[t 检验](https://en.wikipedia.org/wiki/Student%27s_t-test)**。
在 t 检验中,我们计算所谓的 **t 值**,它表示均值之间的差异,同时考虑方差。研究表明,t 值服从 **t 分布**,这使我们能够为给定的置信水平 **p** 获取阈值(可以通过计算或查表获得)。然后,我们将 t 值与该阈值进行比较,以接受或拒绝假设。
在 Python 中,我们可以使用 **SciPy** 包,其中包括 `ttest_ind` 函数(以及许多其他有用的统计函数!)。它为我们计算 t 值,并反向查找置信 p 值,这样我们只需查看置信度即可得出结论。
例如,我们比较一垒手和二垒手身高的结果如下:
```python
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
```
```
T-value = 7.65
P-value: 9.137321189738925e-12
```
在我们的例子中,p 值非常低,这意味着有强有力的证据支持一垒手更高的结论。
我们还可以测试其他类型的假设,例如:
* 证明某个样本符合某种分布。在我们的例子中,我们假设身高是正态分布的,但这需要正式的统计验证。
* 证明样本的均值与某个预定义值相符。
* 比较多个样本的均值(例如,不同年龄组的幸福感差异)。
## 大数法则和中心极限定理
正态分布如此重要的原因之一是所谓的 **中心极限定理**。假设我们有一个独立的 N 个值 X1, ..., XN 的大样本,这些值来自任何均值为 μ、方差为 σ2 的分布。那么,当 N 足够大时(换句话说,当 N→∞),均值 ΣiXi 将服从正态分布,均值为 μ,方差为 σ2/N。
> 中心极限定理的另一种解释是,无论分布如何,当你计算任意随机变量值的和的均值时,最终都会得到正态分布。
根据中心极限定理,当 N→∞ 时,样本均值等于 μ 的概率趋于 1。这被称为 **大数法则**。
## 协方差和相关性
数据科学的一个任务是发现数据之间的关系。当两个序列在同一时间表现出相似的行为时,我们称它们 **相关**,即它们要么同时上升/下降,要么一个序列上升时另一个下降,反之亦然。换句话说,这两个序列之间似乎存在某种关系。
> 相关性并不一定表明两个序列之间存在因果关系;有时两个变量可能依赖于某个外部原因,或者它们的相关性可能纯属偶然。然而,强烈的数学相关性是两个变量某种程度上相互关联的良好指示。
从数学上讲,显示两个随机变量之间关系的主要概念是 **协方差**,其计算公式为:Cov(X,Y) = **E**\[(X-**E**(X))(Y-**E**(Y))\]。我们计算两个变量相对于其均值的偏差,然后将这些偏差相乘。如果两个变量一起偏离,其乘积总是正值,最终得到正协方差。如果两个变量不同步偏离(即一个低于平均值时另一个高于平均值),我们总是得到负值,最终得到负协方差。如果偏差无关,它们的和大致为零。
协方差的绝对值并不能告诉我们相关性的强弱,因为它取决于实际值的大小。为了归一化,我们可以将协方差除以两个变量的标准差,得到 **相关性**。相关性的好处是它总是介于 [-1,1] 之间,其中 1 表示强正相关,-1 表示强负相关,0 表示完全无相关(变量独立)。
**示例**:我们可以计算棒球运动员体重和身高之间的相关性:
```python
print(np.corrcoef(weights,heights))
```
结果是一个 **相关性矩阵**,如下所示:
```
array([[1. , 0.52959196],
[0.52959196, 1. ]])
```
> 相关性矩阵 C 可以针对任意数量的输入序列 S1, ..., Sn 计算。Cij 的值是 Si 和 Sj 之间的相关性,对角线元素总是 1(即 Si 的自相关性)。
在我们的例子中,值 0.53 表明体重和身高之间存在一定的相关性。我们还可以绘制一个散点图,将一个值与另一个值进行比较,以直观地观察它们之间的关系:

> 更多关于相关性和协方差的示例可以在 [附带的笔记本](../../../../1-Introduction/04-stats-and-probability/notebook.ipynb) 中找到。
## 总结
在本节中,我们学习了:
* 数据的基本统计属性,如均值、方差、中位数和四分位数
* 随机变量的不同分布,包括正态分布
* 如何找到不同属性之间的相关性
* 如何使用数学和统计学的严谨工具来验证假设
* 如何根据数据样本计算随机变量的置信区间
虽然这绝不是概率和统计学中所有主题的详尽列表,但它应该足以为您进入本课程提供一个良好的起点。
## 🚀 挑战
使用笔记本中的示例代码测试以下假设:
1. 一垒手比二垒手年长
2. 一垒手比三垒手高
3. 游击手比二垒手高
## [课后测验](https://purple-hill-04aebfb03.1.azurestaticapps.net/quiz/7)
## 复习与自学
概率和统计学是一个非常广泛的主题,值得开设一门独立的课程。如果您有兴趣深入研究理论,可以继续阅读以下书籍:
1. [Carlos Fernandez-Granda](https://cims.nyu.edu/~cfgranda/) 来自纽约大学的优秀讲义 [Probability and Statistics for Data Science](https://cims.nyu.edu/~cfgranda/pages/stuff/probability_stats_for_DS.pdf)(在线可用)
2. [Peter and Andrew Bruce. Practical Statistics for Data Scientists.](https://www.oreilly.com/library/view/practical-statistics-for/9781491952955/) [[R 示例代码](https://github.com/andrewgbruce/statistics-for-data-scientists)]。
3. [James D. Miller. Statistics for Data Science](https://www.packtpub.com/product/statistics-for-data-science/9781788290678) [[R 示例代码](https://github.com/PacktPublishing/Statistics-for-Data-Science)]
## 作业
[小型糖尿病研究](assignment.md)
## 致谢
本课程由 [Dmitry Soshnikov](http://soshnikov.com) 倾情创作。
**免责声明**:
本文档使用AI翻译服务 [Co-op Translator](https://github.com/Azure/co-op-translator) 进行翻译。尽管我们努力确保翻译的准确性,但请注意,自动翻译可能包含错误或不准确之处。原始语言的文档应被视为权威来源。对于重要信息,建议使用专业人工翻译。我们不对因使用此翻译而产生的任何误解或误读承担责任。 这里我们还计算了**四分位距** IQR=Q3-Q1,以及所谓的**离群值**——位于区间 [Q1-1.5*IQR,Q3+1.5*IQR] 之外的值。
对于包含少量可能值的有限分布,一个良好的“典型”值是出现频率最高的值,称为**众数**。众数通常应用于分类数据,例如颜色。考虑一种情况,我们有两组人——一组强烈偏爱红色,另一组偏爱蓝色。如果我们用数字编码颜色,最喜欢的颜色的均值可能会落在橙色或绿色范围,这无法反映任何一组的实际偏好。然而,众数可能是其中一种颜色,或者两种颜色(如果投票人数相等,在这种情况下称为**多众分布**)。
## 真实世界数据
当我们分析现实生活中的数据时,它们通常不是严格意义上的随机变量,因为我们并未进行未知结果的实验。例如,考虑一组棒球运动员及其身体数据,如身高、体重和年龄。这些数字并不完全随机,但我们仍然可以应用相同的数学概念。例如,一组人的体重可以被视为从某个随机变量中抽取的一组值。以下是来自 [美国职业棒球大联盟](http://mlb.mlb.com/index.jsp) 的实际棒球运动员体重序列(数据来源于 [此数据集](http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_MLB_HeightsWeights),为方便起见,仅显示前 20 个值):
```
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
```
> **注意**:要查看使用此数据集的示例,请参阅[配套笔记本](../../../../1-Introduction/04-stats-and-probability/notebook.ipynb)。本课程中还有许多挑战,你可以通过向该笔记本添加代码来完成它们。如果你不确定如何操作数据,不必担心——我们稍后会回到使用 Python 处理数据的部分。如果你不知道如何在 Jupyter Notebook 中运行代码,请查看[这篇文章](https://soshnikov.com/education/how-to-execute-notebooks-from-github/)。
以下是显示我们数据均值、中位数和四分位数的箱形图:

由于我们的数据包含不同球员**角色**的信息,我们还可以按角色绘制箱形图——这将帮助我们了解参数值在不同角色之间的差异。这次我们考虑身高:

该图表表明,平均而言,一垒手的身高高于二垒手的身高。在本课程后面,我们将学习如何更正式地验证这一假设,以及如何证明我们的数据在统计上具有显著性。
> 在处理真实世界数据时,我们假设所有数据点是从某个概率分布中抽取的样本。这个假设使我们能够应用机器学习技术并构建有效的预测模型。
为了查看数据的分布,我们可以绘制一个称为**直方图**的图表。X 轴包含多个不同的体重区间(即所谓的**分箱**),Y 轴显示随机变量样本落入某个区间的次数。

从这个直方图可以看出,所有值都集中在某个平均体重附近,离平均体重越远,出现该体重值的次数越少。也就是说,棒球运动员的体重与平均体重差异很大的可能性非常小。体重的方差显示了体重值与平均值可能的差异程度。
> 如果我们取其他人群的体重数据,而不是棒球联盟的球员,分布可能会有所不同。然而,分布的形状会保持一致,但均值和方差会发生变化。因此,如果我们在棒球运动员上训练模型,当应用于大学学生时可能会产生错误结果,因为底层分布不同。
## 正态分布
我们上面看到的体重分布非常典型,许多现实世界的测量值遵循相同类型的分布,但均值和方差不同。这种分布称为**正态分布**,在统计学中具有非常重要的作用。
使用正态分布是生成潜在棒球运动员随机体重的正确方法。一旦我们知道平均体重 `mean` 和标准差 `std`,我们可以通过以下方式生成 1000 个体重样本:
```python
samples = np.random.normal(mean,std,1000)
```
如果我们绘制生成样本的直方图,会看到与上图非常相似的图像。如果我们增加样本数量和分箱数量,可以生成更接近理想的正态分布图像:

*均值=0,标准差=1 的正态分布*
## 置信区间
当我们讨论棒球运动员的体重时,我们假设存在某个**随机变量 W**,它对应于所有棒球运动员体重的理想概率分布(即所谓的**总体**)。我们的体重序列对应于所有棒球运动员的一个子集,称为**样本**。一个有趣的问题是,我们能否知道 W 的分布参数,即总体的均值和方差?
最简单的答案是计算样本的均值和方差。然而,可能出现我们的随机样本未能准确代表完整总体的情况。因此,谈论**置信区间**是有意义的。
> **置信区间** 是基于我们的样本对总体真实均值的估计,其准确性在某一概率(或 **置信水平**)范围内。
假设我们有一个样本 X1, ..., Xn 来自某个分布。每次从分布中抽取样本时,我们会得到不同的均值 μ。因此,μ 可以被视为一个随机变量。一个置信度为 p 的 **置信区间** 是一对值 (Lp,Rp),使得 **P**(Lp≤μ≤Rp) = p,即测得的均值落在该区间内的概率等于 p。
详细讨论如何计算这些置信区间超出了我们的简短介绍范围。更多细节可以参考 [维基百科](https://en.wikipedia.org/wiki/Confidence_interval)。简而言之,我们定义了相对于总体真实均值的样本均值分布,这被称为 **t 分布**。
> **有趣的事实**:t 分布的名称来源于数学家 William Sealy Gosset,他以笔名 "Student" 发表了相关论文。他当时在健力士啤酒厂工作,据说他的雇主不希望公众知道他们使用统计测试来评估原材料的质量。
如果我们希望以置信度 p 估计总体均值 μ,我们需要取 t 分布 A 的 *(1-p)/2 分位数*,这可以从表格中查得,或者通过统计软件(如 Python、R 等)的内置函数计算。然后,μ 的区间为 X±A*D/√n,其中 X 是样本的均值,D 是标准差。
> **注意**:我们还省略了与 t 分布相关的重要概念 [自由度](https://en.wikipedia.org/wiki/Degrees_of_freedom_(statistics)) 的讨论。您可以参考更完整的统计学书籍以深入理解这一概念。
关于体重和身高的置信区间计算示例可以在 [附带的笔记本](../../../../1-Introduction/04-stats-and-probability/notebook.ipynb) 中找到。
| p | 体重均值 |
|------|---------------|
| 0.85 | 201.73±0.94 |
| 0.90 | 201.73±1.08 |
| 0.95 | 201.73±1.28 |
注意,置信概率越高,置信区间越宽。
## 假设检验
在我们的棒球运动员数据集中,有不同的球员角色,可以总结如下(查看 [附带的笔记本](../../../../1-Introduction/04-stats-and-probability/notebook.ipynb) 了解如何计算此表):
| 角色 | 身高 | 体重 | 数量 |
|-------------------|-----------|-----------|-------|
| 捕手 | 72.723684 | 204.328947 | 76 |
| 指定打击手 | 74.222222 | 220.888889 | 18 |
| 一垒手 | 74.000000 | 213.109091 | 55 |
| 外野手 | 73.010309 | 199.113402 | 194 |
| 救援投手 | 74.374603 | 203.517460 | 315 |
| 二垒手 | 71.362069 | 184.344828 | 58 |
| 游击手 | 71.903846 | 182.923077 | 52 |
| 先发投手 | 74.719457 | 205.163636 | 221 |
| 三垒手 | 73.044444 | 200.955556 | 45 |
我们可以注意到,一垒手的平均身高高于二垒手。因此,我们可能会得出结论:**一垒手比二垒手高**。
> 这个陈述被称为 **假设**,因为我们并不知道这一事实是否真的成立。
然而,是否可以得出这一结论并不总是显而易见的。从上面的讨论中我们知道,每个均值都有一个相关的置信区间,因此这种差异可能只是统计误差。我们需要更正式的方法来检验我们的假设。
让我们分别计算一垒手和二垒手身高的置信区间:
| 置信度 | 一垒手 | 二垒手 |
|--------|---------------|---------------|
| 0.85 | 73.62..74.38 | 71.04..71.69 |
| 0.90 | 73.56..74.44 | 70.99..71.73 |
| 0.95 | 73.47..74.53 | 70.92..71.81 |
我们可以看到,在任何置信度下,这些区间都没有重叠。这证明了我们的假设:一垒手比二垒手高。
更正式地说,我们要解决的问题是判断 **两个概率分布是否相同**,或者至少它们的参数是否相同。根据分布的不同,我们需要使用不同的检验方法。如果我们知道分布是正态分布,我们可以应用 **[t 检验](https://en.wikipedia.org/wiki/Student%27s_t-test)**。
在 t 检验中,我们计算所谓的 **t 值**,它表示均值之间的差异,同时考虑方差。研究表明,t 值服从 **t 分布**,这使我们能够为给定的置信水平 **p** 获取阈值(可以通过计算或查表获得)。然后,我们将 t 值与该阈值进行比较,以接受或拒绝假设。
在 Python 中,我们可以使用 **SciPy** 包,其中包括 `ttest_ind` 函数(以及许多其他有用的统计函数!)。它为我们计算 t 值,并反向查找置信 p 值,这样我们只需查看置信度即可得出结论。
例如,我们比较一垒手和二垒手身高的结果如下:
```python
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
```
```
T-value = 7.65
P-value: 9.137321189738925e-12
```
在我们的例子中,p 值非常低,这意味着有强有力的证据支持一垒手更高的结论。
我们还可以测试其他类型的假设,例如:
* 证明某个样本符合某种分布。在我们的例子中,我们假设身高是正态分布的,但这需要正式的统计验证。
* 证明样本的均值与某个预定义值相符。
* 比较多个样本的均值(例如,不同年龄组的幸福感差异)。
## 大数法则和中心极限定理
正态分布如此重要的原因之一是所谓的 **中心极限定理**。假设我们有一个独立的 N 个值 X1, ..., XN 的大样本,这些值来自任何均值为 μ、方差为 σ2 的分布。那么,当 N 足够大时(换句话说,当 N→∞),均值 ΣiXi 将服从正态分布,均值为 μ,方差为 σ2/N。
> 中心极限定理的另一种解释是,无论分布如何,当你计算任意随机变量值的和的均值时,最终都会得到正态分布。
根据中心极限定理,当 N→∞ 时,样本均值等于 μ 的概率趋于 1。这被称为 **大数法则**。
## 协方差和相关性
数据科学的一个任务是发现数据之间的关系。当两个序列在同一时间表现出相似的行为时,我们称它们 **相关**,即它们要么同时上升/下降,要么一个序列上升时另一个下降,反之亦然。换句话说,这两个序列之间似乎存在某种关系。
> 相关性并不一定表明两个序列之间存在因果关系;有时两个变量可能依赖于某个外部原因,或者它们的相关性可能纯属偶然。然而,强烈的数学相关性是两个变量某种程度上相互关联的良好指示。
从数学上讲,显示两个随机变量之间关系的主要概念是 **协方差**,其计算公式为:Cov(X,Y) = **E**\[(X-**E**(X))(Y-**E**(Y))\]。我们计算两个变量相对于其均值的偏差,然后将这些偏差相乘。如果两个变量一起偏离,其乘积总是正值,最终得到正协方差。如果两个变量不同步偏离(即一个低于平均值时另一个高于平均值),我们总是得到负值,最终得到负协方差。如果偏差无关,它们的和大致为零。
协方差的绝对值并不能告诉我们相关性的强弱,因为它取决于实际值的大小。为了归一化,我们可以将协方差除以两个变量的标准差,得到 **相关性**。相关性的好处是它总是介于 [-1,1] 之间,其中 1 表示强正相关,-1 表示强负相关,0 表示完全无相关(变量独立)。
**示例**:我们可以计算棒球运动员体重和身高之间的相关性:
```python
print(np.corrcoef(weights,heights))
```
结果是一个 **相关性矩阵**,如下所示:
```
array([[1. , 0.52959196],
[0.52959196, 1. ]])
```
> 相关性矩阵 C 可以针对任意数量的输入序列 S1, ..., Sn 计算。Cij 的值是 Si 和 Sj 之间的相关性,对角线元素总是 1(即 Si 的自相关性)。
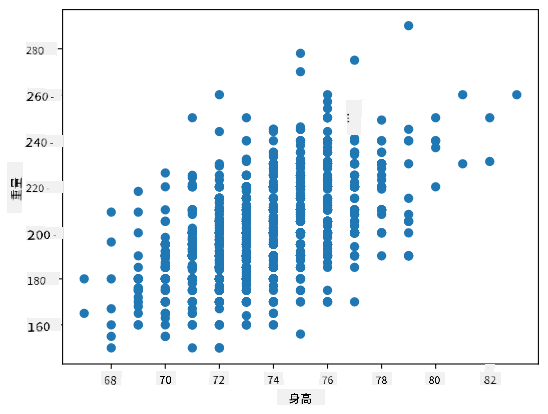
在我们的例子中,值 0.53 表明体重和身高之间存在一定的相关性。我们还可以绘制一个散点图,将一个值与另一个值进行比较,以直观地观察它们之间的关系:

> 更多关于相关性和协方差的示例可以在 [附带的笔记本](../../../../1-Introduction/04-stats-and-probability/notebook.ipynb) 中找到。
## 总结
在本节中,我们学习了:
* 数据的基本统计属性,如均值、方差、中位数和四分位数
* 随机变量的不同分布,包括正态分布
* 如何找到不同属性之间的相关性
* 如何使用数学和统计学的严谨工具来验证假设
* 如何根据数据样本计算随机变量的置信区间
虽然这绝不是概率和统计学中所有主题的详尽列表,但它应该足以为您进入本课程提供一个良好的起点。
## 🚀 挑战
使用笔记本中的示例代码测试以下假设:
1. 一垒手比二垒手年长
2. 一垒手比三垒手高
3. 游击手比二垒手高
## [课后测验](https://purple-hill-04aebfb03.1.azurestaticapps.net/quiz/7)
## 复习与自学
概率和统计学是一个非常广泛的主题,值得开设一门独立的课程。如果您有兴趣深入研究理论,可以继续阅读以下书籍:
1. [Carlos Fernandez-Granda](https://cims.nyu.edu/~cfgranda/) 来自纽约大学的优秀讲义 [Probability and Statistics for Data Science](https://cims.nyu.edu/~cfgranda/pages/stuff/probability_stats_for_DS.pdf)(在线可用)
2. [Peter and Andrew Bruce. Practical Statistics for Data Scientists.](https://www.oreilly.com/library/view/practical-statistics-for/9781491952955/) [[R 示例代码](https://github.com/andrewgbruce/statistics-for-data-scientists)]。
3. [James D. Miller. Statistics for Data Science](https://www.packtpub.com/product/statistics-for-data-science/9781788290678) [[R 示例代码](https://github.com/PacktPublishing/Statistics-for-Data-Science)]
## 作业
[小型糖尿病研究](assignment.md)
## 致谢
本课程由 [Dmitry Soshnikov](http://soshnikov.com) 倾情创作。
**免责声明**:
本文档使用AI翻译服务 [Co-op Translator](https://github.com/Azure/co-op-translator) 进行翻译。尽管我们努力确保翻译的准确性,但请注意,自动翻译可能包含错误或不准确之处。原始语言的文档应被视为权威来源。对于重要信息,建议使用专业人工翻译。我们不对因使用此翻译而产生的任何误解或误读承担责任。
这里我们还计算了**四分位距** IQR=Q3-Q1,以及所谓的**离群值**——位于区间 [Q1-1.5*IQR,Q3+1.5*IQR] 之外的值。
对于包含少量可能值的有限分布,一个良好的“典型”值是出现频率最高的值,称为**众数**。众数通常应用于分类数据,例如颜色。考虑一种情况,我们有两组人——一组强烈偏爱红色,另一组偏爱蓝色。如果我们用数字编码颜色,最喜欢的颜色的均值可能会落在橙色或绿色范围,这无法反映任何一组的实际偏好。然而,众数可能是其中一种颜色,或者两种颜色(如果投票人数相等,在这种情况下称为**多众分布**)。
## 真实世界数据
当我们分析现实生活中的数据时,它们通常不是严格意义上的随机变量,因为我们并未进行未知结果的实验。例如,考虑一组棒球运动员及其身体数据,如身高、体重和年龄。这些数字并不完全随机,但我们仍然可以应用相同的数学概念。例如,一组人的体重可以被视为从某个随机变量中抽取的一组值。以下是来自 [美国职业棒球大联盟](http://mlb.mlb.com/index.jsp) 的实际棒球运动员体重序列(数据来源于 [此数据集](http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_MLB_HeightsWeights),为方便起见,仅显示前 20 个值):
```
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
```
> **注意**:要查看使用此数据集的示例,请参阅[配套笔记本](../../../../1-Introduction/04-stats-and-probability/notebook.ipynb)。本课程中还有许多挑战,你可以通过向该笔记本添加代码来完成它们。如果你不确定如何操作数据,不必担心——我们稍后会回到使用 Python 处理数据的部分。如果你不知道如何在 Jupyter Notebook 中运行代码,请查看[这篇文章](https://soshnikov.com/education/how-to-execute-notebooks-from-github/)。
以下是显示我们数据均值、中位数和四分位数的箱形图:

由于我们的数据包含不同球员**角色**的信息,我们还可以按角色绘制箱形图——这将帮助我们了解参数值在不同角色之间的差异。这次我们考虑身高:

该图表表明,平均而言,一垒手的身高高于二垒手的身高。在本课程后面,我们将学习如何更正式地验证这一假设,以及如何证明我们的数据在统计上具有显著性。
> 在处理真实世界数据时,我们假设所有数据点是从某个概率分布中抽取的样本。这个假设使我们能够应用机器学习技术并构建有效的预测模型。
为了查看数据的分布,我们可以绘制一个称为**直方图**的图表。X 轴包含多个不同的体重区间(即所谓的**分箱**),Y 轴显示随机变量样本落入某个区间的次数。

从这个直方图可以看出,所有值都集中在某个平均体重附近,离平均体重越远,出现该体重值的次数越少。也就是说,棒球运动员的体重与平均体重差异很大的可能性非常小。体重的方差显示了体重值与平均值可能的差异程度。
> 如果我们取其他人群的体重数据,而不是棒球联盟的球员,分布可能会有所不同。然而,分布的形状会保持一致,但均值和方差会发生变化。因此,如果我们在棒球运动员上训练模型,当应用于大学学生时可能会产生错误结果,因为底层分布不同。
## 正态分布
我们上面看到的体重分布非常典型,许多现实世界的测量值遵循相同类型的分布,但均值和方差不同。这种分布称为**正态分布**,在统计学中具有非常重要的作用。
使用正态分布是生成潜在棒球运动员随机体重的正确方法。一旦我们知道平均体重 `mean` 和标准差 `std`,我们可以通过以下方式生成 1000 个体重样本:
```python
samples = np.random.normal(mean,std,1000)
```
如果我们绘制生成样本的直方图,会看到与上图非常相似的图像。如果我们增加样本数量和分箱数量,可以生成更接近理想的正态分布图像:

*均值=0,标准差=1 的正态分布*
## 置信区间
当我们讨论棒球运动员的体重时,我们假设存在某个**随机变量 W**,它对应于所有棒球运动员体重的理想概率分布(即所谓的**总体**)。我们的体重序列对应于所有棒球运动员的一个子集,称为**样本**。一个有趣的问题是,我们能否知道 W 的分布参数,即总体的均值和方差?
最简单的答案是计算样本的均值和方差。然而,可能出现我们的随机样本未能准确代表完整总体的情况。因此,谈论**置信区间**是有意义的。
> **置信区间** 是基于我们的样本对总体真实均值的估计,其准确性在某一概率(或 **置信水平**)范围内。
假设我们有一个样本 X1, ..., Xn 来自某个分布。每次从分布中抽取样本时,我们会得到不同的均值 μ。因此,μ 可以被视为一个随机变量。一个置信度为 p 的 **置信区间** 是一对值 (Lp,Rp),使得 **P**(Lp≤μ≤Rp) = p,即测得的均值落在该区间内的概率等于 p。
详细讨论如何计算这些置信区间超出了我们的简短介绍范围。更多细节可以参考 [维基百科](https://en.wikipedia.org/wiki/Confidence_interval)。简而言之,我们定义了相对于总体真实均值的样本均值分布,这被称为 **t 分布**。
> **有趣的事实**:t 分布的名称来源于数学家 William Sealy Gosset,他以笔名 "Student" 发表了相关论文。他当时在健力士啤酒厂工作,据说他的雇主不希望公众知道他们使用统计测试来评估原材料的质量。
如果我们希望以置信度 p 估计总体均值 μ,我们需要取 t 分布 A 的 *(1-p)/2 分位数*,这可以从表格中查得,或者通过统计软件(如 Python、R 等)的内置函数计算。然后,μ 的区间为 X±A*D/√n,其中 X 是样本的均值,D 是标准差。
> **注意**:我们还省略了与 t 分布相关的重要概念 [自由度](https://en.wikipedia.org/wiki/Degrees_of_freedom_(statistics)) 的讨论。您可以参考更完整的统计学书籍以深入理解这一概念。
关于体重和身高的置信区间计算示例可以在 [附带的笔记本](../../../../1-Introduction/04-stats-and-probability/notebook.ipynb) 中找到。
| p | 体重均值 |
|------|---------------|
| 0.85 | 201.73±0.94 |
| 0.90 | 201.73±1.08 |
| 0.95 | 201.73±1.28 |
注意,置信概率越高,置信区间越宽。
## 假设检验
在我们的棒球运动员数据集中,有不同的球员角色,可以总结如下(查看 [附带的笔记本](../../../../1-Introduction/04-stats-and-probability/notebook.ipynb) 了解如何计算此表):
| 角色 | 身高 | 体重 | 数量 |
|-------------------|-----------|-----------|-------|
| 捕手 | 72.723684 | 204.328947 | 76 |
| 指定打击手 | 74.222222 | 220.888889 | 18 |
| 一垒手 | 74.000000 | 213.109091 | 55 |
| 外野手 | 73.010309 | 199.113402 | 194 |
| 救援投手 | 74.374603 | 203.517460 | 315 |
| 二垒手 | 71.362069 | 184.344828 | 58 |
| 游击手 | 71.903846 | 182.923077 | 52 |
| 先发投手 | 74.719457 | 205.163636 | 221 |
| 三垒手 | 73.044444 | 200.955556 | 45 |
我们可以注意到,一垒手的平均身高高于二垒手。因此,我们可能会得出结论:**一垒手比二垒手高**。
> 这个陈述被称为 **假设**,因为我们并不知道这一事实是否真的成立。
然而,是否可以得出这一结论并不总是显而易见的。从上面的讨论中我们知道,每个均值都有一个相关的置信区间,因此这种差异可能只是统计误差。我们需要更正式的方法来检验我们的假设。
让我们分别计算一垒手和二垒手身高的置信区间:
| 置信度 | 一垒手 | 二垒手 |
|--------|---------------|---------------|
| 0.85 | 73.62..74.38 | 71.04..71.69 |
| 0.90 | 73.56..74.44 | 70.99..71.73 |
| 0.95 | 73.47..74.53 | 70.92..71.81 |
我们可以看到,在任何置信度下,这些区间都没有重叠。这证明了我们的假设:一垒手比二垒手高。
更正式地说,我们要解决的问题是判断 **两个概率分布是否相同**,或者至少它们的参数是否相同。根据分布的不同,我们需要使用不同的检验方法。如果我们知道分布是正态分布,我们可以应用 **[t 检验](https://en.wikipedia.org/wiki/Student%27s_t-test)**。
在 t 检验中,我们计算所谓的 **t 值**,它表示均值之间的差异,同时考虑方差。研究表明,t 值服从 **t 分布**,这使我们能够为给定的置信水平 **p** 获取阈值(可以通过计算或查表获得)。然后,我们将 t 值与该阈值进行比较,以接受或拒绝假设。
在 Python 中,我们可以使用 **SciPy** 包,其中包括 `ttest_ind` 函数(以及许多其他有用的统计函数!)。它为我们计算 t 值,并反向查找置信 p 值,这样我们只需查看置信度即可得出结论。
例如,我们比较一垒手和二垒手身高的结果如下:
```python
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
```
```
T-value = 7.65
P-value: 9.137321189738925e-12
```
在我们的例子中,p 值非常低,这意味着有强有力的证据支持一垒手更高的结论。
我们还可以测试其他类型的假设,例如:
* 证明某个样本符合某种分布。在我们的例子中,我们假设身高是正态分布的,但这需要正式的统计验证。
* 证明样本的均值与某个预定义值相符。
* 比较多个样本的均值(例如,不同年龄组的幸福感差异)。
## 大数法则和中心极限定理
正态分布如此重要的原因之一是所谓的 **中心极限定理**。假设我们有一个独立的 N 个值 X1, ..., XN 的大样本,这些值来自任何均值为 μ、方差为 σ2 的分布。那么,当 N 足够大时(换句话说,当 N→∞),均值 ΣiXi 将服从正态分布,均值为 μ,方差为 σ2/N。
> 中心极限定理的另一种解释是,无论分布如何,当你计算任意随机变量值的和的均值时,最终都会得到正态分布。
根据中心极限定理,当 N→∞ 时,样本均值等于 μ 的概率趋于 1。这被称为 **大数法则**。
## 协方差和相关性
数据科学的一个任务是发现数据之间的关系。当两个序列在同一时间表现出相似的行为时,我们称它们 **相关**,即它们要么同时上升/下降,要么一个序列上升时另一个下降,反之亦然。换句话说,这两个序列之间似乎存在某种关系。
> 相关性并不一定表明两个序列之间存在因果关系;有时两个变量可能依赖于某个外部原因,或者它们的相关性可能纯属偶然。然而,强烈的数学相关性是两个变量某种程度上相互关联的良好指示。
从数学上讲,显示两个随机变量之间关系的主要概念是 **协方差**,其计算公式为:Cov(X,Y) = **E**\[(X-**E**(X))(Y-**E**(Y))\]。我们计算两个变量相对于其均值的偏差,然后将这些偏差相乘。如果两个变量一起偏离,其乘积总是正值,最终得到正协方差。如果两个变量不同步偏离(即一个低于平均值时另一个高于平均值),我们总是得到负值,最终得到负协方差。如果偏差无关,它们的和大致为零。
协方差的绝对值并不能告诉我们相关性的强弱,因为它取决于实际值的大小。为了归一化,我们可以将协方差除以两个变量的标准差,得到 **相关性**。相关性的好处是它总是介于 [-1,1] 之间,其中 1 表示强正相关,-1 表示强负相关,0 表示完全无相关(变量独立)。
**示例**:我们可以计算棒球运动员体重和身高之间的相关性:
```python
print(np.corrcoef(weights,heights))
```
结果是一个 **相关性矩阵**,如下所示:
```
array([[1. , 0.52959196],
[0.52959196, 1. ]])
```
> 相关性矩阵 C 可以针对任意数量的输入序列 S1, ..., Sn 计算。Cij 的值是 Si 和 Sj 之间的相关性,对角线元素总是 1(即 Si 的自相关性)。
在我们的例子中,值 0.53 表明体重和身高之间存在一定的相关性。我们还可以绘制一个散点图,将一个值与另一个值进行比较,以直观地观察它们之间的关系:

> 更多关于相关性和协方差的示例可以在 [附带的笔记本](../../../../1-Introduction/04-stats-and-probability/notebook.ipynb) 中找到。
## 总结
在本节中,我们学习了:
* 数据的基本统计属性,如均值、方差、中位数和四分位数
* 随机变量的不同分布,包括正态分布
* 如何找到不同属性之间的相关性
* 如何使用数学和统计学的严谨工具来验证假设
* 如何根据数据样本计算随机变量的置信区间
虽然这绝不是概率和统计学中所有主题的详尽列表,但它应该足以为您进入本课程提供一个良好的起点。
## 🚀 挑战
使用笔记本中的示例代码测试以下假设:
1. 一垒手比二垒手年长
2. 一垒手比三垒手高
3. 游击手比二垒手高
## [课后测验](https://purple-hill-04aebfb03.1.azurestaticapps.net/quiz/7)
## 复习与自学
概率和统计学是一个非常广泛的主题,值得开设一门独立的课程。如果您有兴趣深入研究理论,可以继续阅读以下书籍:
1. [Carlos Fernandez-Granda](https://cims.nyu.edu/~cfgranda/) 来自纽约大学的优秀讲义 [Probability and Statistics for Data Science](https://cims.nyu.edu/~cfgranda/pages/stuff/probability_stats_for_DS.pdf)(在线可用)
2. [Peter and Andrew Bruce. Practical Statistics for Data Scientists.](https://www.oreilly.com/library/view/practical-statistics-for/9781491952955/) [[R 示例代码](https://github.com/andrewgbruce/statistics-for-data-scientists)]。
3. [James D. Miller. Statistics for Data Science](https://www.packtpub.com/product/statistics-for-data-science/9781788290678) [[R 示例代码](https://github.com/PacktPublishing/Statistics-for-Data-Science)]
## 作业
[小型糖尿病研究](assignment.md)
## 致谢
本课程由 [Dmitry Soshnikov](http://soshnikov.com) 倾情创作。
**免责声明**:
本文档使用AI翻译服务 [Co-op Translator](https://github.com/Azure/co-op-translator) 进行翻译。尽管我们努力确保翻译的准确性,但请注意,自动翻译可能包含错误或不准确之处。原始语言的文档应被视为权威来源。对于重要信息,建议使用专业人工翻译。我们不对因使用此翻译而产生的任何误解或误读承担责任。