# Kratki uvod u statistiku i teoriju vjerojatnosti
| ](../../sketchnotes/04-Statistics-Probability.png)|
|:---:|
| Statistika i vjerojatnost - _Sketchnote od [@nitya](https://twitter.com/nitya)_ |
Statistika i teorija vjerojatnosti su dva usko povezana područja matematike koja su izuzetno važna za znanost o podacima. Iako je moguće raditi s podacima bez dubokog poznavanja matematike, ipak je korisno razumjeti barem osnovne koncepte. Ovdje ćemo predstaviti kratki uvod koji će vam pomoći da započnete.
[](https://youtu.be/Z5Zy85g4Yjw)
## [Kviz prije predavanja](https://purple-hill-04aebfb03.1.azurestaticapps.net/quiz/6)
## Vjerojatnost i slučajne varijable
**Vjerojatnost** je broj između 0 i 1 koji izražava koliko je neki **događaj** vjerojatan. Definira se kao omjer broja pozitivnih ishoda (koji vode do događaja) i ukupnog broja ishoda, pod uvjetom da su svi ishodi jednako vjerojatni. Na primjer, kada bacimo kocku, vjerojatnost da dobijemo paran broj je 3/6 = 0.5.
Kada govorimo o događajima, koristimo **slučajne varijable**. Na primjer, slučajna varijabla koja predstavlja broj dobiven bacanjem kocke može poprimiti vrijednosti od 1 do 6. Skup brojeva od 1 do 6 naziva se **prostor uzorka**. Možemo govoriti o vjerojatnosti da slučajna varijabla poprimi određenu vrijednost, na primjer P(X=3)=1/6.
Slučajna varijabla u prethodnom primjeru naziva se **diskretna**, jer ima prebrojiv prostor uzorka, tj. postoje odvojene vrijednosti koje se mogu nabrojati. Postoje slučajevi kada je prostor uzorka raspon realnih brojeva ili cijeli skup realnih brojeva. Takve varijable nazivaju se **kontinuirane**. Dobar primjer je vrijeme dolaska autobusa.
## Raspodjela vjerojatnosti
U slučaju diskretnih slučajnih varijabli, lako je opisati vjerojatnost svakog događaja pomoću funkcije P(X). Za svaku vrijednost *s* iz prostora uzorka *S* funkcija daje broj između 0 i 1, tako da zbroj svih vrijednosti P(X=s) za sve događaje iznosi 1.
Najpoznatija diskretna raspodjela je **uniformna raspodjela**, u kojoj prostor uzorka ima N elemenata, s jednakom vjerojatnošću od 1/N za svaki od njih.
Teže je opisati raspodjelu vjerojatnosti kontinuirane varijable, s vrijednostima iz nekog intervala [a,b] ili cijelog skupa realnih brojeva ℝ. Razmotrimo slučaj vremena dolaska autobusa. Zapravo, za svako točno vrijeme dolaska *t*, vjerojatnost da autobus stigne točno u to vrijeme je 0!
> Sada znate da se događaji s vjerojatnošću 0 ipak događaju, i to vrlo često! Barem svaki put kad autobus stigne!
Možemo govoriti samo o vjerojatnosti da varijabla padne u određeni interval vrijednosti, npr. P(t1≤X2). U ovom slučaju, raspodjela vjerojatnosti opisana je **funkcijom gustoće vjerojatnosti** p(x), tako da
 Ovdje također izračunavamo **međukvartilni raspon** IQR=Q3-Q1 i tzv. **outliere** - vrijednosti koje leže izvan granica [Q1-1.5*IQR,Q3+1.5*IQR].
Za konačnu raspodjelu koja sadrži mali broj mogućih vrijednosti, dobra "tipična" vrijednost je ona koja se najčešće pojavljuje, a naziva se **mod**. Često se primjenjuje na kategorijske podatke, poput boja. Razmotrite situaciju kada imamo dvije skupine ljudi - jedni koji snažno preferiraju crvenu boju, a drugi plavu. Ako kodiramo boje brojevima, srednja vrijednost za omiljenu boju bila bi negdje u spektru narančasto-zelene, što ne odražava stvarne preferencije nijedne skupine. Međutim, mod bi bio ili jedna od boja, ili obje boje, ako je broj ljudi koji glasaju za njih jednak (u tom slučaju uzorak nazivamo **multimodalnim**).
## Podaci iz stvarnog svijeta
Kada analiziramo podatke iz stvarnog života, oni često nisu slučajne varijable u pravom smislu, u smislu da ne provodimo eksperimente s nepoznatim ishodom. Na primjer, razmotrite tim bejzbol igrača i njihove tjelesne podatke, poput visine, težine i dobi. Ti brojevi nisu baš slučajni, ali i dalje možemo primijeniti iste matematičke koncepte. Na primjer, niz težina ljudi može se smatrati nizom vrijednosti izvučenih iz neke slučajne varijable. Ispod je niz težina stvarnih bejzbol igrača iz [Major League Baseball](http://mlb.mlb.com/index.jsp), preuzet iz [ovog skupa podataka](http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_MLB_HeightsWeights) (za vašu udobnost, prikazane su samo prve 20 vrijednosti):
```
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
```
> **Napomena**: Za primjer rada s ovim skupom podataka, pogledajte [prateću bilježnicu](notebook.ipynb). Tijekom ove lekcije postoji i niz izazova koje možete riješiti dodavanjem koda u tu bilježnicu. Ako niste sigurni kako raditi s podacima, ne brinite - kasnije ćemo se vratiti radu s podacima koristeći Python. Ako ne znate kako pokrenuti kod u Jupyter Notebooku, pogledajte [ovaj članak](https://soshnikov.com/education/how-to-execute-notebooks-from-github/).
Evo box plota koji prikazuje srednju vrijednost, medijan i kvartile za naše podatke:
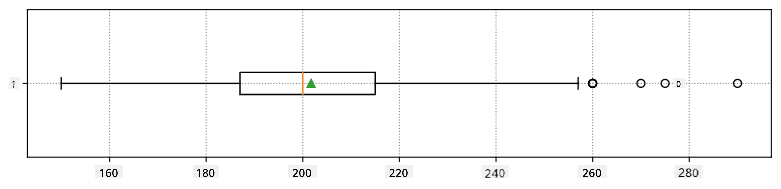
Budući da naši podaci sadrže informacije o različitim **ulogama** igrača, možemo napraviti i box plot prema ulozi - to će nam omogućiti da steknemo uvid u to kako se vrijednosti parametara razlikuju među ulogama. Ovaj put razmotrit ćemo visinu:
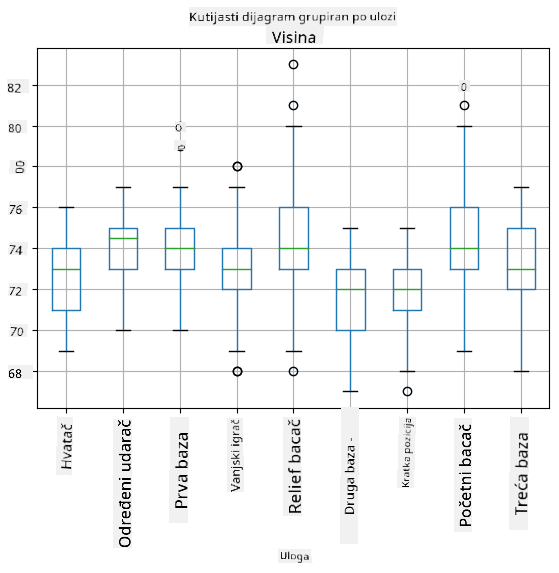
Ovaj dijagram sugerira da je, u prosjeku, visina igrača na prvoj bazi veća od visine igrača na drugoj bazi. Kasnije u ovoj lekciji naučit ćemo kako možemo formalnije testirati ovu hipotezu i kako pokazati da su naši podaci statistički značajni za to.
> Kada radimo s podacima iz stvarnog svijeta, pretpostavljamo da su svi podaci uzorci izvučeni iz neke raspodjele vjerojatnosti. Ova pretpostavka omogućuje nam primjenu tehnika strojnog učenja i izgradnju funkcionalnih prediktivnih modela.
Kako bismo vidjeli kakva je raspodjela naših podataka, možemo nacrtati grafikon zvan **histogram**. X-os bi sadržavala broj različitih intervala težine (tzv. **binova**), a Y-os bi prikazivala broj puta kada je uzorak naše slučajne varijable bio unutar određenog intervala.
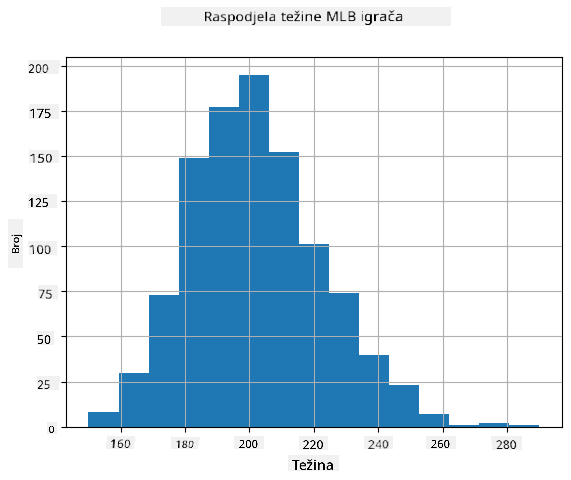
Iz ovog histograma možete vidjeti da su sve vrijednosti centrirane oko određene srednje težine, a što se više udaljavamo od te težine, to se rjeđe susreću težine te vrijednosti. Drugim riječima, vrlo je malo vjerojatno da će težina bejzbol igrača biti vrlo različita od srednje težine. Varijanca težina pokazuje u kojoj mjeri težine odstupaju od srednje vrijednosti.
> Ako uzmemo težine drugih ljudi, koji nisu iz bejzbol lige, raspodjela će vjerojatno biti drugačija. Međutim, oblik raspodjele ostat će isti, ali srednja vrijednost i varijanca će se promijeniti. Dakle, ako treniramo naš model na bejzbol igračima, vjerojatno će dati pogrešne rezultate kada se primijeni na studente sveučilišta, jer je osnovna raspodjela drugačija.
## Normalna raspodjela
Raspodjela težina koju smo vidjeli gore vrlo je tipična, i mnoge mjere iz stvarnog svijeta slijede isti tip raspodjele, ali s različitim srednjim vrijednostima i varijancama. Ova raspodjela naziva se **normalna raspodjela**, i igra vrlo važnu ulogu u statistici.
Korištenje normalne raspodjele ispravan je način za generiranje slučajnih težina potencijalnih bejzbol igrača. Kada znamo srednju težinu `mean` i standardnu devijaciju `std`, možemo generirati 1000 uzoraka težine na sljedeći način:
```python
samples = np.random.normal(mean,std,1000)
```
Ako nacrtamo histogram generiranih uzoraka, vidjet ćemo sliku vrlo sličnu onoj prikazanoj gore. A ako povećamo broj uzoraka i broj binova, možemo generirati sliku normalne raspodjele koja je bliža idealnoj:
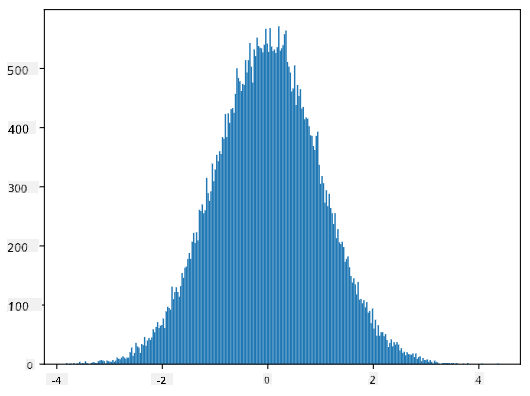
*Normalna raspodjela sa srednjom vrijednošću=0 i std.dev=1*
## Intervali pouzdanosti
Kada govorimo o težinama bejzbol igrača, pretpostavljamo da postoji određena **slučajna varijabla W** koja odgovara idealnoj raspodjeli vjerojatnosti težina svih bejzbol igrača (tzv. **populacija**). Naš niz težina odgovara podskupu svih bejzbol igrača koji nazivamo **uzorak**. Zanimljivo pitanje je, možemo li znati parametre raspodjele W, tj. srednju vrijednost i varijancu populacije?
Najjednostavniji odgovor bio bi izračunati srednju vrijednost i varijancu našeg uzorka. Međutim, moglo bi se dogoditi da naš slučajni uzorak ne predstavlja točno cijelu populaciju. Stoga ima smisla govoriti o **intervalu pouzdanosti**.
> **Interval pouzdanosti** predstavlja procjenu stvarnog srednjeg vrijednosti populacije na temelju našeg uzorka, koja je točna s određenom vjerojatnošću (ili **razinom pouzdanosti**).
Pretpostavimo da imamo uzorak X1, ..., Xn iz naše distribucije. Svaki put kada uzmemo uzorak iz distribucije, dobit ćemo različitu srednju vrijednost μ. Stoga se μ može smatrati slučajnom varijablom. **Interval pouzdanosti** s pouzdanošću p je par vrijednosti (Lp, Rp), takav da **P**(Lp≤μ≤Rp) = p, tj. vjerojatnost da izmjerena srednja vrijednost padne unutar intervala jednaka je p.
Detaljna rasprava o tome kako se ti intervali pouzdanosti izračunavaju prelazi okvire ovog kratkog uvoda. Više detalja možete pronaći [na Wikipediji](https://en.wikipedia.org/wiki/Confidence_interval). Ukratko, definiramo distribuciju izračunate srednje vrijednosti uzorka u odnosu na stvarnu srednju vrijednost populacije, što se naziva **Studentova distribucija**.
> **Zanimljiva činjenica**: Studentova distribucija nazvana je po matematičaru Williamu Sealyju Gossetu, koji je svoj rad objavio pod pseudonimom "Student". Radio je u pivovari Guinness, a prema jednoj verziji, njegov poslodavac nije želio da šira javnost zna da koriste statističke testove za određivanje kvalitete sirovina.
Ako želimo procijeniti srednju vrijednost μ naše populacije s pouzdanošću p, trebamo uzeti *(1-p)/2-ti percentil* Studentove distribucije A, koji se može pronaći u tablicama ili izračunati pomoću ugrađenih funkcija statističkog softvera (npr. Python, R, itd.). Tada bi interval za μ bio X±A*D/√n, gdje je X dobivena srednja vrijednost uzorka, a D standardna devijacija.
> **Napomena**: Također izostavljamo raspravu o važnom konceptu [stupnjeva slobode](https://en.wikipedia.org/wiki/Degrees_of_freedom_(statistics)), koji je važan u vezi sa Studentovom distribucijom. Za dublje razumijevanje ovog koncepta možete se obratiti potpunijim knjigama o statistici.
Primjer izračuna intervala pouzdanosti za težine i visine dan je u [priloženim bilježnicama](notebook.ipynb).
| p | Srednja težina |
|-----|-----------|
| 0.85 | 201.73±0.94 |
| 0.90 | 201.73±1.08 |
| 0.95 | 201.73±1.28 |
Primijetite da što je veća vjerojatnost pouzdanosti, to je širi interval pouzdanosti.
## Testiranje hipoteza
U našem skupu podataka o igračima bejzbola postoje različite uloge igrača, koje se mogu sažeti u tablici ispod (pogledajte [priloženu bilježnicu](notebook.ipynb) kako biste vidjeli kako se ova tablica može izračunati):
| Uloga | Visina | Težina | Broj |
|------|--------|--------|-------|
| Catcher | 72.723684 | 204.328947 | 76 |
| Designated_Hitter | 74.222222 | 220.888889 | 18 |
| First_Baseman | 74.000000 | 213.109091 | 55 |
| Outfielder | 73.010309 | 199.113402 | 194 |
| Relief_Pitcher | 74.374603 | 203.517460 | 315 |
| Second_Baseman | 71.362069 | 184.344828 | 58 |
| Shortstop | 71.903846 | 182.923077 | 52 |
| Starting_Pitcher | 74.719457 | 205.163636 | 221 |
| Third_Baseman | 73.044444 | 200.955556 | 45 |
Možemo primijetiti da je prosječna visina igrača na prvoj bazi veća od one na drugoj bazi. Stoga bismo mogli zaključiti da su **igrači na prvoj bazi viši od igrača na drugoj bazi**.
> Ova izjava naziva se **hipoteza**, jer ne znamo je li činjenica zapravo istinita ili ne.
Međutim, nije uvijek očito možemo li donijeti ovaj zaključak. Iz prethodne rasprave znamo da svaka srednja vrijednost ima pridruženi interval pouzdanosti, pa ta razlika može biti samo statistička pogreška. Potrebno nam je formalniji način za testiranje naše hipoteze.
Izračunajmo intervale pouzdanosti zasebno za visine igrača na prvoj i drugoj bazi:
| Pouzdanost | Prva baza | Druga baza |
|------------|---------------|----------------|
| 0.85 | 73.62..74.38 | 71.04..71.69 |
| 0.90 | 73.56..74.44 | 70.99..71.73 |
| 0.95 | 73.47..74.53 | 70.92..71.81 |
Možemo vidjeti da se intervali ne preklapaju ni pod jednom razinom pouzdanosti. To dokazuje našu hipotezu da su igrači na prvoj bazi viši od igrača na drugoj bazi.
Formalnije, problem koji rješavamo je utvrditi jesu li **dvije distribucije vjerojatnosti iste**, ili barem imaju li iste parametre. Ovisno o distribuciji, za to trebamo koristiti različite testove. Ako znamo da su naše distribucije normalne, možemo primijeniti **[Studentov t-test](https://en.wikipedia.org/wiki/Student%27s_t-test)**.
U Studentovom t-testu izračunavamo tzv. **t-vrijednost**, koja pokazuje razliku između srednjih vrijednosti, uzimajući u obzir varijancu. Pokazano je da t-vrijednost slijedi **Studentovu distribuciju**, što nam omogućuje dobivanje granične vrijednosti za zadanu razinu pouzdanosti **p** (to se može izračunati ili pronaći u numeričkim tablicama). Zatim uspoređujemo t-vrijednost s ovom granicom kako bismo prihvatili ili odbacili hipotezu.
U Pythonu možemo koristiti paket **SciPy**, koji uključuje funkciju `ttest_ind` (uz mnoge druge korisne statističke funkcije!). Ona za nas izračunava t-vrijednost i također obavlja obrnuto traženje p-vrijednosti pouzdanosti, tako da možemo samo pogledati pouzdanost kako bismo donijeli zaključak.
Na primjer, naša usporedba visina igrača na prvoj i drugoj bazi daje nam sljedeće rezultate:
```python
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
```
```
T-value = 7.65
P-value: 9.137321189738925e-12
```
U našem slučaju, p-vrijednost je vrlo niska, što znači da postoje snažni dokazi koji podupiru tvrdnju da su igrači na prvoj bazi viši.
Postoje i druge vrste hipoteza koje bismo mogli testirati, na primjer:
* Dokazati da određeni uzorak slijedi neku distribuciju. U našem slučaju pretpostavili smo da su visine normalno distribuirane, ali to treba formalno statistički provjeriti.
* Dokazati da srednja vrijednost uzorka odgovara nekoj unaprijed definiranoj vrijednosti
* Usporediti srednje vrijednosti više uzoraka (npr. koja je razlika u razinama sreće među različitim dobnim skupinama)
## Zakon velikih brojeva i centralni granični teorem
Jedan od razloga zašto je normalna distribucija toliko važna je tzv. **centralni granični teorem**. Pretpostavimo da imamo veliki uzorak neovisnih N vrijednosti X1, ..., XN, uzorkovanih iz bilo koje distribucije sa srednjom vrijednošću μ i varijancom σ2. Tada, za dovoljno velik N (drugim riječima, kada N→∞), srednja vrijednost ΣiXi bit će normalno distribuirana, sa srednjom vrijednošću μ i varijancom σ2/N.
> Drugi način interpretacije centralnog graničnog teorema je reći da, bez obzira na distribuciju, kada izračunate srednju vrijednost zbroja bilo kojih slučajnih varijabli, završavate s normalnom distribucijom.
Iz centralnog graničnog teorema također slijedi da, kada N→∞, vjerojatnost da srednja vrijednost uzorka bude jednaka μ postaje 1. Ovo je poznato kao **zakon velikih brojeva**.
## Kovarijanca i korelacija
Jedna od stvari koje Data Science radi je pronalaženje odnosa između podataka. Kažemo da se dvije sekvence **koreliraju** kada pokazuju slično ponašanje u isto vrijeme, tj. ili rastu/padaju istovremeno, ili jedna sekvenca raste dok druga pada i obrnuto. Drugim riječima, čini se da postoji neka veza između dvije sekvence.
> Korelacija ne mora nužno ukazivati na uzročnu vezu između dvije sekvence; ponekad obje varijable mogu ovisiti o nekom vanjskom uzroku, ili može biti čista slučajnost da se dvije sekvence koreliraju. Međutim, jaka matematička korelacija dobar je pokazatelj da su dvije varijable na neki način povezane.
Matematički, glavni koncept koji pokazuje odnos između dvije slučajne varijable je **kovarijanca**, koja se izračunava ovako: Cov(X,Y) = **E**\[(X-**E**(X))(Y-**E**(Y))\]. Izračunavamo odstupanje obje varijable od njihovih srednjih vrijednosti, a zatim produkt tih odstupanja. Ako obje varijable odstupaju zajedno, produkt će uvijek biti pozitivna vrijednost, što će rezultirati pozitivnom kovarijansom. Ako obje varijable odstupaju nesinkronizirano (tj. jedna pada ispod prosjeka dok druga raste iznad prosjeka), uvijek ćemo dobiti negativne brojeve, što će rezultirati negativnom kovarijansom. Ako odstupanja nisu ovisna, zbrojit će se na približno nulu.
Apsolutna vrijednost kovarijance ne govori nam mnogo o tome koliko je jaka korelacija, jer ovisi o veličini stvarnih vrijednosti. Da bismo je normalizirali, možemo podijeliti kovarijancu sa standardnom devijacijom obje varijable kako bismo dobili **korelaciju**. Dobra stvar je što je korelacija uvijek u rasponu [-1,1], gdje 1 označava jaku pozitivnu korelaciju između vrijednosti, -1 jaku negativnu korelaciju, a 0 nikakvu korelaciju (varijable su neovisne).
**Primjer**: Možemo izračunati korelaciju između težina i visina igrača bejzbola iz gore spomenutog skupa podataka:
```python
print(np.corrcoef(weights,heights))
```
Kao rezultat, dobivamo **matricu korelacije** poput ove:
```
array([[1. , 0.52959196],
[0.52959196, 1. ]])
```
> Matrica korelacije C može se izračunati za bilo koji broj ulaznih sekvenci S1, ..., Sn. Vrijednost Cij je korelacija između Si i Sj, a dijagonalni elementi su uvijek 1 (što je također samokorelacija Si).
U našem slučaju, vrijednost 0.53 ukazuje na to da postoji određena korelacija između težine i visine osobe. Također možemo napraviti scatter plot jedne vrijednosti u odnosu na drugu kako bismo vizualno vidjeli odnos:
> Više primjera korelacije i kovarijance možete pronaći u [priloženoj bilježnici](notebook.ipynb).
## Zaključak
U ovom odjeljku naučili smo:
* osnovna statistička svojstva podataka, poput srednje vrijednosti, varijance, moda i kvartila
* različite distribucije slučajnih varijabli, uključujući normalnu distribuciju
* kako pronaći korelaciju između različitih svojstava
* kako koristiti matematički i statistički aparat za dokazivanje hipoteza
* kako izračunati intervale pouzdanosti za slučajnu varijablu na temelju uzorka podataka
Iako ovo definitivno nije iscrpan popis tema unutar vjerojatnosti i statistike, trebao bi biti dovoljan za dobar početak ovog tečaja.
## 🚀 Izazov
Koristite uzorak koda u bilježnici za testiranje drugih hipoteza:
1. Igrači na prvoj bazi su stariji od igrača na drugoj bazi
2. Igrači na prvoj bazi su viši od igrača na trećoj bazi
3. Shortstopovi su viši od igrača na drugoj bazi
## [Kviz nakon predavanja](https://purple-hill-04aebfb03.1.azurestaticapps.net/quiz/7)
## Pregled i samostalno učenje
Vjerojatnost i statistika su toliko široka tema da zaslužuju vlastiti tečaj. Ako želite dublje ući u teoriju, možda biste željeli nastaviti čitati neke od sljedećih knjiga:
1. [Carlos Fernandez-Granda](https://cims.nyu.edu/~cfgranda/) s New York University ima odlične bilješke s predavanja [Probability and Statistics for Data Science](https://cims.nyu.edu/~cfgranda/pages/stuff/probability_stats_for_DS.pdf) (dostupno online)
1. [Peter i Andrew Bruce. Practical Statistics for Data Scientists.](https://www.oreilly.com/library/view/practical-statistics-for/9781491952955/) [[uzorak koda u R](https://github.com/andrewgbruce/statistics-for-data-scientists)].
1. [James D. Miller. Statistics for Data Science](https://www.packtpub.com/product/statistics-for-data-science/9781788290678) [[uzorak koda u R](https://github.com/PacktPublishing/Statistics-for-Data-Science)]
## Zadatak
[Mala studija o dijabetesu](assignment.md)
## Zasluge
Ovu lekciju napisao je s ♥️ [Dmitry Soshnikov](http://soshnikov.com)
---
**Odricanje od odgovornosti**:
Ovaj dokument je preveden pomoću AI usluge za prevođenje [Co-op Translator](https://github.com/Azure/co-op-translator). Iako nastojimo osigurati točnost, imajte na umu da automatski prijevodi mogu sadržavati pogreške ili netočnosti. Izvorni dokument na izvornom jeziku treba smatrati autoritativnim izvorom. Za kritične informacije preporučuje se profesionalni prijevod od strane čovjeka. Ne preuzimamo odgovornost za bilo kakva nesporazuma ili pogrešna tumačenja koja proizlaze iz korištenja ovog prijevoda.
Ovdje također izračunavamo **međukvartilni raspon** IQR=Q3-Q1 i tzv. **outliere** - vrijednosti koje leže izvan granica [Q1-1.5*IQR,Q3+1.5*IQR].
Za konačnu raspodjelu koja sadrži mali broj mogućih vrijednosti, dobra "tipična" vrijednost je ona koja se najčešće pojavljuje, a naziva se **mod**. Često se primjenjuje na kategorijske podatke, poput boja. Razmotrite situaciju kada imamo dvije skupine ljudi - jedni koji snažno preferiraju crvenu boju, a drugi plavu. Ako kodiramo boje brojevima, srednja vrijednost za omiljenu boju bila bi negdje u spektru narančasto-zelene, što ne odražava stvarne preferencije nijedne skupine. Međutim, mod bi bio ili jedna od boja, ili obje boje, ako je broj ljudi koji glasaju za njih jednak (u tom slučaju uzorak nazivamo **multimodalnim**).
## Podaci iz stvarnog svijeta
Kada analiziramo podatke iz stvarnog života, oni često nisu slučajne varijable u pravom smislu, u smislu da ne provodimo eksperimente s nepoznatim ishodom. Na primjer, razmotrite tim bejzbol igrača i njihove tjelesne podatke, poput visine, težine i dobi. Ti brojevi nisu baš slučajni, ali i dalje možemo primijeniti iste matematičke koncepte. Na primjer, niz težina ljudi može se smatrati nizom vrijednosti izvučenih iz neke slučajne varijable. Ispod je niz težina stvarnih bejzbol igrača iz [Major League Baseball](http://mlb.mlb.com/index.jsp), preuzet iz [ovog skupa podataka](http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_MLB_HeightsWeights) (za vašu udobnost, prikazane su samo prve 20 vrijednosti):
```
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
```
> **Napomena**: Za primjer rada s ovim skupom podataka, pogledajte [prateću bilježnicu](notebook.ipynb). Tijekom ove lekcije postoji i niz izazova koje možete riješiti dodavanjem koda u tu bilježnicu. Ako niste sigurni kako raditi s podacima, ne brinite - kasnije ćemo se vratiti radu s podacima koristeći Python. Ako ne znate kako pokrenuti kod u Jupyter Notebooku, pogledajte [ovaj članak](https://soshnikov.com/education/how-to-execute-notebooks-from-github/).
Evo box plota koji prikazuje srednju vrijednost, medijan i kvartile za naše podatke:

Budući da naši podaci sadrže informacije o različitim **ulogama** igrača, možemo napraviti i box plot prema ulozi - to će nam omogućiti da steknemo uvid u to kako se vrijednosti parametara razlikuju među ulogama. Ovaj put razmotrit ćemo visinu:

Ovaj dijagram sugerira da je, u prosjeku, visina igrača na prvoj bazi veća od visine igrača na drugoj bazi. Kasnije u ovoj lekciji naučit ćemo kako možemo formalnije testirati ovu hipotezu i kako pokazati da su naši podaci statistički značajni za to.
> Kada radimo s podacima iz stvarnog svijeta, pretpostavljamo da su svi podaci uzorci izvučeni iz neke raspodjele vjerojatnosti. Ova pretpostavka omogućuje nam primjenu tehnika strojnog učenja i izgradnju funkcionalnih prediktivnih modela.
Kako bismo vidjeli kakva je raspodjela naših podataka, možemo nacrtati grafikon zvan **histogram**. X-os bi sadržavala broj različitih intervala težine (tzv. **binova**), a Y-os bi prikazivala broj puta kada je uzorak naše slučajne varijable bio unutar određenog intervala.

Iz ovog histograma možete vidjeti da su sve vrijednosti centrirane oko određene srednje težine, a što se više udaljavamo od te težine, to se rjeđe susreću težine te vrijednosti. Drugim riječima, vrlo je malo vjerojatno da će težina bejzbol igrača biti vrlo različita od srednje težine. Varijanca težina pokazuje u kojoj mjeri težine odstupaju od srednje vrijednosti.
> Ako uzmemo težine drugih ljudi, koji nisu iz bejzbol lige, raspodjela će vjerojatno biti drugačija. Međutim, oblik raspodjele ostat će isti, ali srednja vrijednost i varijanca će se promijeniti. Dakle, ako treniramo naš model na bejzbol igračima, vjerojatno će dati pogrešne rezultate kada se primijeni na studente sveučilišta, jer je osnovna raspodjela drugačija.
## Normalna raspodjela
Raspodjela težina koju smo vidjeli gore vrlo je tipična, i mnoge mjere iz stvarnog svijeta slijede isti tip raspodjele, ali s različitim srednjim vrijednostima i varijancama. Ova raspodjela naziva se **normalna raspodjela**, i igra vrlo važnu ulogu u statistici.
Korištenje normalne raspodjele ispravan je način za generiranje slučajnih težina potencijalnih bejzbol igrača. Kada znamo srednju težinu `mean` i standardnu devijaciju `std`, možemo generirati 1000 uzoraka težine na sljedeći način:
```python
samples = np.random.normal(mean,std,1000)
```
Ako nacrtamo histogram generiranih uzoraka, vidjet ćemo sliku vrlo sličnu onoj prikazanoj gore. A ako povećamo broj uzoraka i broj binova, možemo generirati sliku normalne raspodjele koja je bliža idealnoj:

*Normalna raspodjela sa srednjom vrijednošću=0 i std.dev=1*
## Intervali pouzdanosti
Kada govorimo o težinama bejzbol igrača, pretpostavljamo da postoji određena **slučajna varijabla W** koja odgovara idealnoj raspodjeli vjerojatnosti težina svih bejzbol igrača (tzv. **populacija**). Naš niz težina odgovara podskupu svih bejzbol igrača koji nazivamo **uzorak**. Zanimljivo pitanje je, možemo li znati parametre raspodjele W, tj. srednju vrijednost i varijancu populacije?
Najjednostavniji odgovor bio bi izračunati srednju vrijednost i varijancu našeg uzorka. Međutim, moglo bi se dogoditi da naš slučajni uzorak ne predstavlja točno cijelu populaciju. Stoga ima smisla govoriti o **intervalu pouzdanosti**.
> **Interval pouzdanosti** predstavlja procjenu stvarnog srednjeg vrijednosti populacije na temelju našeg uzorka, koja je točna s određenom vjerojatnošću (ili **razinom pouzdanosti**).
Pretpostavimo da imamo uzorak X1, ..., Xn iz naše distribucije. Svaki put kada uzmemo uzorak iz distribucije, dobit ćemo različitu srednju vrijednost μ. Stoga se μ može smatrati slučajnom varijablom. **Interval pouzdanosti** s pouzdanošću p je par vrijednosti (Lp, Rp), takav da **P**(Lp≤μ≤Rp) = p, tj. vjerojatnost da izmjerena srednja vrijednost padne unutar intervala jednaka je p.
Detaljna rasprava o tome kako se ti intervali pouzdanosti izračunavaju prelazi okvire ovog kratkog uvoda. Više detalja možete pronaći [na Wikipediji](https://en.wikipedia.org/wiki/Confidence_interval). Ukratko, definiramo distribuciju izračunate srednje vrijednosti uzorka u odnosu na stvarnu srednju vrijednost populacije, što se naziva **Studentova distribucija**.
> **Zanimljiva činjenica**: Studentova distribucija nazvana je po matematičaru Williamu Sealyju Gossetu, koji je svoj rad objavio pod pseudonimom "Student". Radio je u pivovari Guinness, a prema jednoj verziji, njegov poslodavac nije želio da šira javnost zna da koriste statističke testove za određivanje kvalitete sirovina.
Ako želimo procijeniti srednju vrijednost μ naše populacije s pouzdanošću p, trebamo uzeti *(1-p)/2-ti percentil* Studentove distribucije A, koji se može pronaći u tablicama ili izračunati pomoću ugrađenih funkcija statističkog softvera (npr. Python, R, itd.). Tada bi interval za μ bio X±A*D/√n, gdje je X dobivena srednja vrijednost uzorka, a D standardna devijacija.
> **Napomena**: Također izostavljamo raspravu o važnom konceptu [stupnjeva slobode](https://en.wikipedia.org/wiki/Degrees_of_freedom_(statistics)), koji je važan u vezi sa Studentovom distribucijom. Za dublje razumijevanje ovog koncepta možete se obratiti potpunijim knjigama o statistici.
Primjer izračuna intervala pouzdanosti za težine i visine dan je u [priloženim bilježnicama](notebook.ipynb).
| p | Srednja težina |
|-----|-----------|
| 0.85 | 201.73±0.94 |
| 0.90 | 201.73±1.08 |
| 0.95 | 201.73±1.28 |
Primijetite da što je veća vjerojatnost pouzdanosti, to je širi interval pouzdanosti.
## Testiranje hipoteza
U našem skupu podataka o igračima bejzbola postoje različite uloge igrača, koje se mogu sažeti u tablici ispod (pogledajte [priloženu bilježnicu](notebook.ipynb) kako biste vidjeli kako se ova tablica može izračunati):
| Uloga | Visina | Težina | Broj |
|------|--------|--------|-------|
| Catcher | 72.723684 | 204.328947 | 76 |
| Designated_Hitter | 74.222222 | 220.888889 | 18 |
| First_Baseman | 74.000000 | 213.109091 | 55 |
| Outfielder | 73.010309 | 199.113402 | 194 |
| Relief_Pitcher | 74.374603 | 203.517460 | 315 |
| Second_Baseman | 71.362069 | 184.344828 | 58 |
| Shortstop | 71.903846 | 182.923077 | 52 |
| Starting_Pitcher | 74.719457 | 205.163636 | 221 |
| Third_Baseman | 73.044444 | 200.955556 | 45 |
Možemo primijetiti da je prosječna visina igrača na prvoj bazi veća od one na drugoj bazi. Stoga bismo mogli zaključiti da su **igrači na prvoj bazi viši od igrača na drugoj bazi**.
> Ova izjava naziva se **hipoteza**, jer ne znamo je li činjenica zapravo istinita ili ne.
Međutim, nije uvijek očito možemo li donijeti ovaj zaključak. Iz prethodne rasprave znamo da svaka srednja vrijednost ima pridruženi interval pouzdanosti, pa ta razlika može biti samo statistička pogreška. Potrebno nam je formalniji način za testiranje naše hipoteze.
Izračunajmo intervale pouzdanosti zasebno za visine igrača na prvoj i drugoj bazi:
| Pouzdanost | Prva baza | Druga baza |
|------------|---------------|----------------|
| 0.85 | 73.62..74.38 | 71.04..71.69 |
| 0.90 | 73.56..74.44 | 70.99..71.73 |
| 0.95 | 73.47..74.53 | 70.92..71.81 |
Možemo vidjeti da se intervali ne preklapaju ni pod jednom razinom pouzdanosti. To dokazuje našu hipotezu da su igrači na prvoj bazi viši od igrača na drugoj bazi.
Formalnije, problem koji rješavamo je utvrditi jesu li **dvije distribucije vjerojatnosti iste**, ili barem imaju li iste parametre. Ovisno o distribuciji, za to trebamo koristiti različite testove. Ako znamo da su naše distribucije normalne, možemo primijeniti **[Studentov t-test](https://en.wikipedia.org/wiki/Student%27s_t-test)**.
U Studentovom t-testu izračunavamo tzv. **t-vrijednost**, koja pokazuje razliku između srednjih vrijednosti, uzimajući u obzir varijancu. Pokazano je da t-vrijednost slijedi **Studentovu distribuciju**, što nam omogućuje dobivanje granične vrijednosti za zadanu razinu pouzdanosti **p** (to se može izračunati ili pronaći u numeričkim tablicama). Zatim uspoređujemo t-vrijednost s ovom granicom kako bismo prihvatili ili odbacili hipotezu.
U Pythonu možemo koristiti paket **SciPy**, koji uključuje funkciju `ttest_ind` (uz mnoge druge korisne statističke funkcije!). Ona za nas izračunava t-vrijednost i također obavlja obrnuto traženje p-vrijednosti pouzdanosti, tako da možemo samo pogledati pouzdanost kako bismo donijeli zaključak.
Na primjer, naša usporedba visina igrača na prvoj i drugoj bazi daje nam sljedeće rezultate:
```python
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
```
```
T-value = 7.65
P-value: 9.137321189738925e-12
```
U našem slučaju, p-vrijednost je vrlo niska, što znači da postoje snažni dokazi koji podupiru tvrdnju da su igrači na prvoj bazi viši.
Postoje i druge vrste hipoteza koje bismo mogli testirati, na primjer:
* Dokazati da određeni uzorak slijedi neku distribuciju. U našem slučaju pretpostavili smo da su visine normalno distribuirane, ali to treba formalno statistički provjeriti.
* Dokazati da srednja vrijednost uzorka odgovara nekoj unaprijed definiranoj vrijednosti
* Usporediti srednje vrijednosti više uzoraka (npr. koja je razlika u razinama sreće među različitim dobnim skupinama)
## Zakon velikih brojeva i centralni granični teorem
Jedan od razloga zašto je normalna distribucija toliko važna je tzv. **centralni granični teorem**. Pretpostavimo da imamo veliki uzorak neovisnih N vrijednosti X1, ..., XN, uzorkovanih iz bilo koje distribucije sa srednjom vrijednošću μ i varijancom σ2. Tada, za dovoljno velik N (drugim riječima, kada N→∞), srednja vrijednost ΣiXi bit će normalno distribuirana, sa srednjom vrijednošću μ i varijancom σ2/N.
> Drugi način interpretacije centralnog graničnog teorema je reći da, bez obzira na distribuciju, kada izračunate srednju vrijednost zbroja bilo kojih slučajnih varijabli, završavate s normalnom distribucijom.
Iz centralnog graničnog teorema također slijedi da, kada N→∞, vjerojatnost da srednja vrijednost uzorka bude jednaka μ postaje 1. Ovo je poznato kao **zakon velikih brojeva**.
## Kovarijanca i korelacija
Jedna od stvari koje Data Science radi je pronalaženje odnosa između podataka. Kažemo da se dvije sekvence **koreliraju** kada pokazuju slično ponašanje u isto vrijeme, tj. ili rastu/padaju istovremeno, ili jedna sekvenca raste dok druga pada i obrnuto. Drugim riječima, čini se da postoji neka veza između dvije sekvence.
> Korelacija ne mora nužno ukazivati na uzročnu vezu između dvije sekvence; ponekad obje varijable mogu ovisiti o nekom vanjskom uzroku, ili može biti čista slučajnost da se dvije sekvence koreliraju. Međutim, jaka matematička korelacija dobar je pokazatelj da su dvije varijable na neki način povezane.
Matematički, glavni koncept koji pokazuje odnos između dvije slučajne varijable je **kovarijanca**, koja se izračunava ovako: Cov(X,Y) = **E**\[(X-**E**(X))(Y-**E**(Y))\]. Izračunavamo odstupanje obje varijable od njihovih srednjih vrijednosti, a zatim produkt tih odstupanja. Ako obje varijable odstupaju zajedno, produkt će uvijek biti pozitivna vrijednost, što će rezultirati pozitivnom kovarijansom. Ako obje varijable odstupaju nesinkronizirano (tj. jedna pada ispod prosjeka dok druga raste iznad prosjeka), uvijek ćemo dobiti negativne brojeve, što će rezultirati negativnom kovarijansom. Ako odstupanja nisu ovisna, zbrojit će se na približno nulu.
Apsolutna vrijednost kovarijance ne govori nam mnogo o tome koliko je jaka korelacija, jer ovisi o veličini stvarnih vrijednosti. Da bismo je normalizirali, možemo podijeliti kovarijancu sa standardnom devijacijom obje varijable kako bismo dobili **korelaciju**. Dobra stvar je što je korelacija uvijek u rasponu [-1,1], gdje 1 označava jaku pozitivnu korelaciju između vrijednosti, -1 jaku negativnu korelaciju, a 0 nikakvu korelaciju (varijable su neovisne).
**Primjer**: Možemo izračunati korelaciju između težina i visina igrača bejzbola iz gore spomenutog skupa podataka:
```python
print(np.corrcoef(weights,heights))
```
Kao rezultat, dobivamo **matricu korelacije** poput ove:
```
array([[1. , 0.52959196],
[0.52959196, 1. ]])
```
> Matrica korelacije C može se izračunati za bilo koji broj ulaznih sekvenci S1, ..., Sn. Vrijednost Cij je korelacija između Si i Sj, a dijagonalni elementi su uvijek 1 (što je također samokorelacija Si).
U našem slučaju, vrijednost 0.53 ukazuje na to da postoji određena korelacija između težine i visine osobe. Također možemo napraviti scatter plot jedne vrijednosti u odnosu na drugu kako bismo vizualno vidjeli odnos:

> Više primjera korelacije i kovarijance možete pronaći u [priloženoj bilježnici](notebook.ipynb).
## Zaključak
U ovom odjeljku naučili smo:
* osnovna statistička svojstva podataka, poput srednje vrijednosti, varijance, moda i kvartila
* različite distribucije slučajnih varijabli, uključujući normalnu distribuciju
* kako pronaći korelaciju između različitih svojstava
* kako koristiti matematički i statistički aparat za dokazivanje hipoteza
* kako izračunati intervale pouzdanosti za slučajnu varijablu na temelju uzorka podataka
Iako ovo definitivno nije iscrpan popis tema unutar vjerojatnosti i statistike, trebao bi biti dovoljan za dobar početak ovog tečaja.
## 🚀 Izazov
Koristite uzorak koda u bilježnici za testiranje drugih hipoteza:
1. Igrači na prvoj bazi su stariji od igrača na drugoj bazi
2. Igrači na prvoj bazi su viši od igrača na trećoj bazi
3. Shortstopovi su viši od igrača na drugoj bazi
## [Kviz nakon predavanja](https://purple-hill-04aebfb03.1.azurestaticapps.net/quiz/7)
## Pregled i samostalno učenje
Vjerojatnost i statistika su toliko široka tema da zaslužuju vlastiti tečaj. Ako želite dublje ući u teoriju, možda biste željeli nastaviti čitati neke od sljedećih knjiga:
1. [Carlos Fernandez-Granda](https://cims.nyu.edu/~cfgranda/) s New York University ima odlične bilješke s predavanja [Probability and Statistics for Data Science](https://cims.nyu.edu/~cfgranda/pages/stuff/probability_stats_for_DS.pdf) (dostupno online)
1. [Peter i Andrew Bruce. Practical Statistics for Data Scientists.](https://www.oreilly.com/library/view/practical-statistics-for/9781491952955/) [[uzorak koda u R](https://github.com/andrewgbruce/statistics-for-data-scientists)].
1. [James D. Miller. Statistics for Data Science](https://www.packtpub.com/product/statistics-for-data-science/9781788290678) [[uzorak koda u R](https://github.com/PacktPublishing/Statistics-for-Data-Science)]
## Zadatak
[Mala studija o dijabetesu](assignment.md)
## Zasluge
Ovu lekciju napisao je s ♥️ [Dmitry Soshnikov](http://soshnikov.com)
---
**Odricanje od odgovornosti**:
Ovaj dokument je preveden pomoću AI usluge za prevođenje [Co-op Translator](https://github.com/Azure/co-op-translator). Iako nastojimo osigurati točnost, imajte na umu da automatski prijevodi mogu sadržavati pogreške ili netočnosti. Izvorni dokument na izvornom jeziku treba smatrati autoritativnim izvorom. Za kritične informacije preporučuje se profesionalni prijevod od strane čovjeka. Ne preuzimamo odgovornost za bilo kakva nesporazuma ili pogrešna tumačenja koja proizlaze iz korištenja ovog prijevoda. Ovdje također izračunavamo **međukvartilni raspon** IQR=Q3-Q1 i tzv. **outliere** - vrijednosti koje leže izvan granica [Q1-1.5*IQR,Q3+1.5*IQR].
Za konačnu raspodjelu koja sadrži mali broj mogućih vrijednosti, dobra "tipična" vrijednost je ona koja se najčešće pojavljuje, a naziva se **mod**. Često se primjenjuje na kategorijske podatke, poput boja. Razmotrite situaciju kada imamo dvije skupine ljudi - jedni koji snažno preferiraju crvenu boju, a drugi plavu. Ako kodiramo boje brojevima, srednja vrijednost za omiljenu boju bila bi negdje u spektru narančasto-zelene, što ne odražava stvarne preferencije nijedne skupine. Međutim, mod bi bio ili jedna od boja, ili obje boje, ako je broj ljudi koji glasaju za njih jednak (u tom slučaju uzorak nazivamo **multimodalnim**).
## Podaci iz stvarnog svijeta
Kada analiziramo podatke iz stvarnog života, oni često nisu slučajne varijable u pravom smislu, u smislu da ne provodimo eksperimente s nepoznatim ishodom. Na primjer, razmotrite tim bejzbol igrača i njihove tjelesne podatke, poput visine, težine i dobi. Ti brojevi nisu baš slučajni, ali i dalje možemo primijeniti iste matematičke koncepte. Na primjer, niz težina ljudi može se smatrati nizom vrijednosti izvučenih iz neke slučajne varijable. Ispod je niz težina stvarnih bejzbol igrača iz [Major League Baseball](http://mlb.mlb.com/index.jsp), preuzet iz [ovog skupa podataka](http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_MLB_HeightsWeights) (za vašu udobnost, prikazane su samo prve 20 vrijednosti):
```
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
```
> **Napomena**: Za primjer rada s ovim skupom podataka, pogledajte [prateću bilježnicu](notebook.ipynb). Tijekom ove lekcije postoji i niz izazova koje možete riješiti dodavanjem koda u tu bilježnicu. Ako niste sigurni kako raditi s podacima, ne brinite - kasnije ćemo se vratiti radu s podacima koristeći Python. Ako ne znate kako pokrenuti kod u Jupyter Notebooku, pogledajte [ovaj članak](https://soshnikov.com/education/how-to-execute-notebooks-from-github/).
Evo box plota koji prikazuje srednju vrijednost, medijan i kvartile za naše podatke:

Budući da naši podaci sadrže informacije o različitim **ulogama** igrača, možemo napraviti i box plot prema ulozi - to će nam omogućiti da steknemo uvid u to kako se vrijednosti parametara razlikuju među ulogama. Ovaj put razmotrit ćemo visinu:

Ovaj dijagram sugerira da je, u prosjeku, visina igrača na prvoj bazi veća od visine igrača na drugoj bazi. Kasnije u ovoj lekciji naučit ćemo kako možemo formalnije testirati ovu hipotezu i kako pokazati da su naši podaci statistički značajni za to.
> Kada radimo s podacima iz stvarnog svijeta, pretpostavljamo da su svi podaci uzorci izvučeni iz neke raspodjele vjerojatnosti. Ova pretpostavka omogućuje nam primjenu tehnika strojnog učenja i izgradnju funkcionalnih prediktivnih modela.
Kako bismo vidjeli kakva je raspodjela naših podataka, možemo nacrtati grafikon zvan **histogram**. X-os bi sadržavala broj različitih intervala težine (tzv. **binova**), a Y-os bi prikazivala broj puta kada je uzorak naše slučajne varijable bio unutar određenog intervala.

Iz ovog histograma možete vidjeti da su sve vrijednosti centrirane oko određene srednje težine, a što se više udaljavamo od te težine, to se rjeđe susreću težine te vrijednosti. Drugim riječima, vrlo je malo vjerojatno da će težina bejzbol igrača biti vrlo različita od srednje težine. Varijanca težina pokazuje u kojoj mjeri težine odstupaju od srednje vrijednosti.
> Ako uzmemo težine drugih ljudi, koji nisu iz bejzbol lige, raspodjela će vjerojatno biti drugačija. Međutim, oblik raspodjele ostat će isti, ali srednja vrijednost i varijanca će se promijeniti. Dakle, ako treniramo naš model na bejzbol igračima, vjerojatno će dati pogrešne rezultate kada se primijeni na studente sveučilišta, jer je osnovna raspodjela drugačija.
## Normalna raspodjela
Raspodjela težina koju smo vidjeli gore vrlo je tipična, i mnoge mjere iz stvarnog svijeta slijede isti tip raspodjele, ali s različitim srednjim vrijednostima i varijancama. Ova raspodjela naziva se **normalna raspodjela**, i igra vrlo važnu ulogu u statistici.
Korištenje normalne raspodjele ispravan je način za generiranje slučajnih težina potencijalnih bejzbol igrača. Kada znamo srednju težinu `mean` i standardnu devijaciju `std`, možemo generirati 1000 uzoraka težine na sljedeći način:
```python
samples = np.random.normal(mean,std,1000)
```
Ako nacrtamo histogram generiranih uzoraka, vidjet ćemo sliku vrlo sličnu onoj prikazanoj gore. A ako povećamo broj uzoraka i broj binova, možemo generirati sliku normalne raspodjele koja je bliža idealnoj:

*Normalna raspodjela sa srednjom vrijednošću=0 i std.dev=1*
## Intervali pouzdanosti
Kada govorimo o težinama bejzbol igrača, pretpostavljamo da postoji određena **slučajna varijabla W** koja odgovara idealnoj raspodjeli vjerojatnosti težina svih bejzbol igrača (tzv. **populacija**). Naš niz težina odgovara podskupu svih bejzbol igrača koji nazivamo **uzorak**. Zanimljivo pitanje je, možemo li znati parametre raspodjele W, tj. srednju vrijednost i varijancu populacije?
Najjednostavniji odgovor bio bi izračunati srednju vrijednost i varijancu našeg uzorka. Međutim, moglo bi se dogoditi da naš slučajni uzorak ne predstavlja točno cijelu populaciju. Stoga ima smisla govoriti o **intervalu pouzdanosti**.
> **Interval pouzdanosti** predstavlja procjenu stvarnog srednjeg vrijednosti populacije na temelju našeg uzorka, koja je točna s određenom vjerojatnošću (ili **razinom pouzdanosti**).
Pretpostavimo da imamo uzorak X1, ..., Xn iz naše distribucije. Svaki put kada uzmemo uzorak iz distribucije, dobit ćemo različitu srednju vrijednost μ. Stoga se μ može smatrati slučajnom varijablom. **Interval pouzdanosti** s pouzdanošću p je par vrijednosti (Lp, Rp), takav da **P**(Lp≤μ≤Rp) = p, tj. vjerojatnost da izmjerena srednja vrijednost padne unutar intervala jednaka je p.
Detaljna rasprava o tome kako se ti intervali pouzdanosti izračunavaju prelazi okvire ovog kratkog uvoda. Više detalja možete pronaći [na Wikipediji](https://en.wikipedia.org/wiki/Confidence_interval). Ukratko, definiramo distribuciju izračunate srednje vrijednosti uzorka u odnosu na stvarnu srednju vrijednost populacije, što se naziva **Studentova distribucija**.
> **Zanimljiva činjenica**: Studentova distribucija nazvana je po matematičaru Williamu Sealyju Gossetu, koji je svoj rad objavio pod pseudonimom "Student". Radio je u pivovari Guinness, a prema jednoj verziji, njegov poslodavac nije želio da šira javnost zna da koriste statističke testove za određivanje kvalitete sirovina.
Ako želimo procijeniti srednju vrijednost μ naše populacije s pouzdanošću p, trebamo uzeti *(1-p)/2-ti percentil* Studentove distribucije A, koji se može pronaći u tablicama ili izračunati pomoću ugrađenih funkcija statističkog softvera (npr. Python, R, itd.). Tada bi interval za μ bio X±A*D/√n, gdje je X dobivena srednja vrijednost uzorka, a D standardna devijacija.
> **Napomena**: Također izostavljamo raspravu o važnom konceptu [stupnjeva slobode](https://en.wikipedia.org/wiki/Degrees_of_freedom_(statistics)), koji je važan u vezi sa Studentovom distribucijom. Za dublje razumijevanje ovog koncepta možete se obratiti potpunijim knjigama o statistici.
Primjer izračuna intervala pouzdanosti za težine i visine dan je u [priloženim bilježnicama](notebook.ipynb).
| p | Srednja težina |
|-----|-----------|
| 0.85 | 201.73±0.94 |
| 0.90 | 201.73±1.08 |
| 0.95 | 201.73±1.28 |
Primijetite da što je veća vjerojatnost pouzdanosti, to je širi interval pouzdanosti.
## Testiranje hipoteza
U našem skupu podataka o igračima bejzbola postoje različite uloge igrača, koje se mogu sažeti u tablici ispod (pogledajte [priloženu bilježnicu](notebook.ipynb) kako biste vidjeli kako se ova tablica može izračunati):
| Uloga | Visina | Težina | Broj |
|------|--------|--------|-------|
| Catcher | 72.723684 | 204.328947 | 76 |
| Designated_Hitter | 74.222222 | 220.888889 | 18 |
| First_Baseman | 74.000000 | 213.109091 | 55 |
| Outfielder | 73.010309 | 199.113402 | 194 |
| Relief_Pitcher | 74.374603 | 203.517460 | 315 |
| Second_Baseman | 71.362069 | 184.344828 | 58 |
| Shortstop | 71.903846 | 182.923077 | 52 |
| Starting_Pitcher | 74.719457 | 205.163636 | 221 |
| Third_Baseman | 73.044444 | 200.955556 | 45 |
Možemo primijetiti da je prosječna visina igrača na prvoj bazi veća od one na drugoj bazi. Stoga bismo mogli zaključiti da su **igrači na prvoj bazi viši od igrača na drugoj bazi**.
> Ova izjava naziva se **hipoteza**, jer ne znamo je li činjenica zapravo istinita ili ne.
Međutim, nije uvijek očito možemo li donijeti ovaj zaključak. Iz prethodne rasprave znamo da svaka srednja vrijednost ima pridruženi interval pouzdanosti, pa ta razlika može biti samo statistička pogreška. Potrebno nam je formalniji način za testiranje naše hipoteze.
Izračunajmo intervale pouzdanosti zasebno za visine igrača na prvoj i drugoj bazi:
| Pouzdanost | Prva baza | Druga baza |
|------------|---------------|----------------|
| 0.85 | 73.62..74.38 | 71.04..71.69 |
| 0.90 | 73.56..74.44 | 70.99..71.73 |
| 0.95 | 73.47..74.53 | 70.92..71.81 |
Možemo vidjeti da se intervali ne preklapaju ni pod jednom razinom pouzdanosti. To dokazuje našu hipotezu da su igrači na prvoj bazi viši od igrača na drugoj bazi.
Formalnije, problem koji rješavamo je utvrditi jesu li **dvije distribucije vjerojatnosti iste**, ili barem imaju li iste parametre. Ovisno o distribuciji, za to trebamo koristiti različite testove. Ako znamo da su naše distribucije normalne, možemo primijeniti **[Studentov t-test](https://en.wikipedia.org/wiki/Student%27s_t-test)**.
U Studentovom t-testu izračunavamo tzv. **t-vrijednost**, koja pokazuje razliku između srednjih vrijednosti, uzimajući u obzir varijancu. Pokazano je da t-vrijednost slijedi **Studentovu distribuciju**, što nam omogućuje dobivanje granične vrijednosti za zadanu razinu pouzdanosti **p** (to se može izračunati ili pronaći u numeričkim tablicama). Zatim uspoređujemo t-vrijednost s ovom granicom kako bismo prihvatili ili odbacili hipotezu.
U Pythonu možemo koristiti paket **SciPy**, koji uključuje funkciju `ttest_ind` (uz mnoge druge korisne statističke funkcije!). Ona za nas izračunava t-vrijednost i također obavlja obrnuto traženje p-vrijednosti pouzdanosti, tako da možemo samo pogledati pouzdanost kako bismo donijeli zaključak.
Na primjer, naša usporedba visina igrača na prvoj i drugoj bazi daje nam sljedeće rezultate:
```python
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
```
```
T-value = 7.65
P-value: 9.137321189738925e-12
```
U našem slučaju, p-vrijednost je vrlo niska, što znači da postoje snažni dokazi koji podupiru tvrdnju da su igrači na prvoj bazi viši.
Postoje i druge vrste hipoteza koje bismo mogli testirati, na primjer:
* Dokazati da određeni uzorak slijedi neku distribuciju. U našem slučaju pretpostavili smo da su visine normalno distribuirane, ali to treba formalno statistički provjeriti.
* Dokazati da srednja vrijednost uzorka odgovara nekoj unaprijed definiranoj vrijednosti
* Usporediti srednje vrijednosti više uzoraka (npr. koja je razlika u razinama sreće među različitim dobnim skupinama)
## Zakon velikih brojeva i centralni granični teorem
Jedan od razloga zašto je normalna distribucija toliko važna je tzv. **centralni granični teorem**. Pretpostavimo da imamo veliki uzorak neovisnih N vrijednosti X1, ..., XN, uzorkovanih iz bilo koje distribucije sa srednjom vrijednošću μ i varijancom σ2. Tada, za dovoljno velik N (drugim riječima, kada N→∞), srednja vrijednost ΣiXi bit će normalno distribuirana, sa srednjom vrijednošću μ i varijancom σ2/N.
> Drugi način interpretacije centralnog graničnog teorema je reći da, bez obzira na distribuciju, kada izračunate srednju vrijednost zbroja bilo kojih slučajnih varijabli, završavate s normalnom distribucijom.
Iz centralnog graničnog teorema također slijedi da, kada N→∞, vjerojatnost da srednja vrijednost uzorka bude jednaka μ postaje 1. Ovo je poznato kao **zakon velikih brojeva**.
## Kovarijanca i korelacija
Jedna od stvari koje Data Science radi je pronalaženje odnosa između podataka. Kažemo da se dvije sekvence **koreliraju** kada pokazuju slično ponašanje u isto vrijeme, tj. ili rastu/padaju istovremeno, ili jedna sekvenca raste dok druga pada i obrnuto. Drugim riječima, čini se da postoji neka veza između dvije sekvence.
> Korelacija ne mora nužno ukazivati na uzročnu vezu između dvije sekvence; ponekad obje varijable mogu ovisiti o nekom vanjskom uzroku, ili može biti čista slučajnost da se dvije sekvence koreliraju. Međutim, jaka matematička korelacija dobar je pokazatelj da su dvije varijable na neki način povezane.
Matematički, glavni koncept koji pokazuje odnos između dvije slučajne varijable je **kovarijanca**, koja se izračunava ovako: Cov(X,Y) = **E**\[(X-**E**(X))(Y-**E**(Y))\]. Izračunavamo odstupanje obje varijable od njihovih srednjih vrijednosti, a zatim produkt tih odstupanja. Ako obje varijable odstupaju zajedno, produkt će uvijek biti pozitivna vrijednost, što će rezultirati pozitivnom kovarijansom. Ako obje varijable odstupaju nesinkronizirano (tj. jedna pada ispod prosjeka dok druga raste iznad prosjeka), uvijek ćemo dobiti negativne brojeve, što će rezultirati negativnom kovarijansom. Ako odstupanja nisu ovisna, zbrojit će se na približno nulu.
Apsolutna vrijednost kovarijance ne govori nam mnogo o tome koliko je jaka korelacija, jer ovisi o veličini stvarnih vrijednosti. Da bismo je normalizirali, možemo podijeliti kovarijancu sa standardnom devijacijom obje varijable kako bismo dobili **korelaciju**. Dobra stvar je što je korelacija uvijek u rasponu [-1,1], gdje 1 označava jaku pozitivnu korelaciju između vrijednosti, -1 jaku negativnu korelaciju, a 0 nikakvu korelaciju (varijable su neovisne).
**Primjer**: Možemo izračunati korelaciju između težina i visina igrača bejzbola iz gore spomenutog skupa podataka:
```python
print(np.corrcoef(weights,heights))
```
Kao rezultat, dobivamo **matricu korelacije** poput ove:
```
array([[1. , 0.52959196],
[0.52959196, 1. ]])
```
> Matrica korelacije C može se izračunati za bilo koji broj ulaznih sekvenci S1, ..., Sn. Vrijednost Cij je korelacija između Si i Sj, a dijagonalni elementi su uvijek 1 (što je također samokorelacija Si).
U našem slučaju, vrijednost 0.53 ukazuje na to da postoji određena korelacija između težine i visine osobe. Također možemo napraviti scatter plot jedne vrijednosti u odnosu na drugu kako bismo vizualno vidjeli odnos:

> Više primjera korelacije i kovarijance možete pronaći u [priloženoj bilježnici](notebook.ipynb).
## Zaključak
U ovom odjeljku naučili smo:
* osnovna statistička svojstva podataka, poput srednje vrijednosti, varijance, moda i kvartila
* različite distribucije slučajnih varijabli, uključujući normalnu distribuciju
* kako pronaći korelaciju između različitih svojstava
* kako koristiti matematički i statistički aparat za dokazivanje hipoteza
* kako izračunati intervale pouzdanosti za slučajnu varijablu na temelju uzorka podataka
Iako ovo definitivno nije iscrpan popis tema unutar vjerojatnosti i statistike, trebao bi biti dovoljan za dobar početak ovog tečaja.
## 🚀 Izazov
Koristite uzorak koda u bilježnici za testiranje drugih hipoteza:
1. Igrači na prvoj bazi su stariji od igrača na drugoj bazi
2. Igrači na prvoj bazi su viši od igrača na trećoj bazi
3. Shortstopovi su viši od igrača na drugoj bazi
## [Kviz nakon predavanja](https://purple-hill-04aebfb03.1.azurestaticapps.net/quiz/7)
## Pregled i samostalno učenje
Vjerojatnost i statistika su toliko široka tema da zaslužuju vlastiti tečaj. Ako želite dublje ući u teoriju, možda biste željeli nastaviti čitati neke od sljedećih knjiga:
1. [Carlos Fernandez-Granda](https://cims.nyu.edu/~cfgranda/) s New York University ima odlične bilješke s predavanja [Probability and Statistics for Data Science](https://cims.nyu.edu/~cfgranda/pages/stuff/probability_stats_for_DS.pdf) (dostupno online)
1. [Peter i Andrew Bruce. Practical Statistics for Data Scientists.](https://www.oreilly.com/library/view/practical-statistics-for/9781491952955/) [[uzorak koda u R](https://github.com/andrewgbruce/statistics-for-data-scientists)].
1. [James D. Miller. Statistics for Data Science](https://www.packtpub.com/product/statistics-for-data-science/9781788290678) [[uzorak koda u R](https://github.com/PacktPublishing/Statistics-for-Data-Science)]
## Zadatak
[Mala studija o dijabetesu](assignment.md)
## Zasluge
Ovu lekciju napisao je s ♥️ [Dmitry Soshnikov](http://soshnikov.com)
---
**Odricanje od odgovornosti**:
Ovaj dokument je preveden pomoću AI usluge za prevođenje [Co-op Translator](https://github.com/Azure/co-op-translator). Iako nastojimo osigurati točnost, imajte na umu da automatski prijevodi mogu sadržavati pogreške ili netočnosti. Izvorni dokument na izvornom jeziku treba smatrati autoritativnim izvorom. Za kritične informacije preporučuje se profesionalni prijevod od strane čovjeka. Ne preuzimamo odgovornost za bilo kakva nesporazuma ili pogrešna tumačenja koja proizlaze iz korištenja ovog prijevoda.
Ovdje također izračunavamo **međukvartilni raspon** IQR=Q3-Q1 i tzv. **outliere** - vrijednosti koje leže izvan granica [Q1-1.5*IQR,Q3+1.5*IQR].
Za konačnu raspodjelu koja sadrži mali broj mogućih vrijednosti, dobra "tipična" vrijednost je ona koja se najčešće pojavljuje, a naziva se **mod**. Često se primjenjuje na kategorijske podatke, poput boja. Razmotrite situaciju kada imamo dvije skupine ljudi - jedni koji snažno preferiraju crvenu boju, a drugi plavu. Ako kodiramo boje brojevima, srednja vrijednost za omiljenu boju bila bi negdje u spektru narančasto-zelene, što ne odražava stvarne preferencije nijedne skupine. Međutim, mod bi bio ili jedna od boja, ili obje boje, ako je broj ljudi koji glasaju za njih jednak (u tom slučaju uzorak nazivamo **multimodalnim**).
## Podaci iz stvarnog svijeta
Kada analiziramo podatke iz stvarnog života, oni često nisu slučajne varijable u pravom smislu, u smislu da ne provodimo eksperimente s nepoznatim ishodom. Na primjer, razmotrite tim bejzbol igrača i njihove tjelesne podatke, poput visine, težine i dobi. Ti brojevi nisu baš slučajni, ali i dalje možemo primijeniti iste matematičke koncepte. Na primjer, niz težina ljudi može se smatrati nizom vrijednosti izvučenih iz neke slučajne varijable. Ispod je niz težina stvarnih bejzbol igrača iz [Major League Baseball](http://mlb.mlb.com/index.jsp), preuzet iz [ovog skupa podataka](http://wiki.stat.ucla.edu/socr/index.php/SOCR_Data_MLB_HeightsWeights) (za vašu udobnost, prikazane su samo prve 20 vrijednosti):
```
[180.0, 215.0, 210.0, 210.0, 188.0, 176.0, 209.0, 200.0, 231.0, 180.0, 188.0, 180.0, 185.0, 160.0, 180.0, 185.0, 197.0, 189.0, 185.0, 219.0]
```
> **Napomena**: Za primjer rada s ovim skupom podataka, pogledajte [prateću bilježnicu](notebook.ipynb). Tijekom ove lekcije postoji i niz izazova koje možete riješiti dodavanjem koda u tu bilježnicu. Ako niste sigurni kako raditi s podacima, ne brinite - kasnije ćemo se vratiti radu s podacima koristeći Python. Ako ne znate kako pokrenuti kod u Jupyter Notebooku, pogledajte [ovaj članak](https://soshnikov.com/education/how-to-execute-notebooks-from-github/).
Evo box plota koji prikazuje srednju vrijednost, medijan i kvartile za naše podatke:

Budući da naši podaci sadrže informacije o različitim **ulogama** igrača, možemo napraviti i box plot prema ulozi - to će nam omogućiti da steknemo uvid u to kako se vrijednosti parametara razlikuju među ulogama. Ovaj put razmotrit ćemo visinu:

Ovaj dijagram sugerira da je, u prosjeku, visina igrača na prvoj bazi veća od visine igrača na drugoj bazi. Kasnije u ovoj lekciji naučit ćemo kako možemo formalnije testirati ovu hipotezu i kako pokazati da su naši podaci statistički značajni za to.
> Kada radimo s podacima iz stvarnog svijeta, pretpostavljamo da su svi podaci uzorci izvučeni iz neke raspodjele vjerojatnosti. Ova pretpostavka omogućuje nam primjenu tehnika strojnog učenja i izgradnju funkcionalnih prediktivnih modela.
Kako bismo vidjeli kakva je raspodjela naših podataka, možemo nacrtati grafikon zvan **histogram**. X-os bi sadržavala broj različitih intervala težine (tzv. **binova**), a Y-os bi prikazivala broj puta kada je uzorak naše slučajne varijable bio unutar određenog intervala.

Iz ovog histograma možete vidjeti da su sve vrijednosti centrirane oko određene srednje težine, a što se više udaljavamo od te težine, to se rjeđe susreću težine te vrijednosti. Drugim riječima, vrlo je malo vjerojatno da će težina bejzbol igrača biti vrlo različita od srednje težine. Varijanca težina pokazuje u kojoj mjeri težine odstupaju od srednje vrijednosti.
> Ako uzmemo težine drugih ljudi, koji nisu iz bejzbol lige, raspodjela će vjerojatno biti drugačija. Međutim, oblik raspodjele ostat će isti, ali srednja vrijednost i varijanca će se promijeniti. Dakle, ako treniramo naš model na bejzbol igračima, vjerojatno će dati pogrešne rezultate kada se primijeni na studente sveučilišta, jer je osnovna raspodjela drugačija.
## Normalna raspodjela
Raspodjela težina koju smo vidjeli gore vrlo je tipična, i mnoge mjere iz stvarnog svijeta slijede isti tip raspodjele, ali s različitim srednjim vrijednostima i varijancama. Ova raspodjela naziva se **normalna raspodjela**, i igra vrlo važnu ulogu u statistici.
Korištenje normalne raspodjele ispravan je način za generiranje slučajnih težina potencijalnih bejzbol igrača. Kada znamo srednju težinu `mean` i standardnu devijaciju `std`, možemo generirati 1000 uzoraka težine na sljedeći način:
```python
samples = np.random.normal(mean,std,1000)
```
Ako nacrtamo histogram generiranih uzoraka, vidjet ćemo sliku vrlo sličnu onoj prikazanoj gore. A ako povećamo broj uzoraka i broj binova, možemo generirati sliku normalne raspodjele koja je bliža idealnoj:

*Normalna raspodjela sa srednjom vrijednošću=0 i std.dev=1*
## Intervali pouzdanosti
Kada govorimo o težinama bejzbol igrača, pretpostavljamo da postoji određena **slučajna varijabla W** koja odgovara idealnoj raspodjeli vjerojatnosti težina svih bejzbol igrača (tzv. **populacija**). Naš niz težina odgovara podskupu svih bejzbol igrača koji nazivamo **uzorak**. Zanimljivo pitanje je, možemo li znati parametre raspodjele W, tj. srednju vrijednost i varijancu populacije?
Najjednostavniji odgovor bio bi izračunati srednju vrijednost i varijancu našeg uzorka. Međutim, moglo bi se dogoditi da naš slučajni uzorak ne predstavlja točno cijelu populaciju. Stoga ima smisla govoriti o **intervalu pouzdanosti**.
> **Interval pouzdanosti** predstavlja procjenu stvarnog srednjeg vrijednosti populacije na temelju našeg uzorka, koja je točna s određenom vjerojatnošću (ili **razinom pouzdanosti**).
Pretpostavimo da imamo uzorak X1, ..., Xn iz naše distribucije. Svaki put kada uzmemo uzorak iz distribucije, dobit ćemo različitu srednju vrijednost μ. Stoga se μ može smatrati slučajnom varijablom. **Interval pouzdanosti** s pouzdanošću p je par vrijednosti (Lp, Rp), takav da **P**(Lp≤μ≤Rp) = p, tj. vjerojatnost da izmjerena srednja vrijednost padne unutar intervala jednaka je p.
Detaljna rasprava o tome kako se ti intervali pouzdanosti izračunavaju prelazi okvire ovog kratkog uvoda. Više detalja možete pronaći [na Wikipediji](https://en.wikipedia.org/wiki/Confidence_interval). Ukratko, definiramo distribuciju izračunate srednje vrijednosti uzorka u odnosu na stvarnu srednju vrijednost populacije, što se naziva **Studentova distribucija**.
> **Zanimljiva činjenica**: Studentova distribucija nazvana je po matematičaru Williamu Sealyju Gossetu, koji je svoj rad objavio pod pseudonimom "Student". Radio je u pivovari Guinness, a prema jednoj verziji, njegov poslodavac nije želio da šira javnost zna da koriste statističke testove za određivanje kvalitete sirovina.
Ako želimo procijeniti srednju vrijednost μ naše populacije s pouzdanošću p, trebamo uzeti *(1-p)/2-ti percentil* Studentove distribucije A, koji se može pronaći u tablicama ili izračunati pomoću ugrađenih funkcija statističkog softvera (npr. Python, R, itd.). Tada bi interval za μ bio X±A*D/√n, gdje je X dobivena srednja vrijednost uzorka, a D standardna devijacija.
> **Napomena**: Također izostavljamo raspravu o važnom konceptu [stupnjeva slobode](https://en.wikipedia.org/wiki/Degrees_of_freedom_(statistics)), koji je važan u vezi sa Studentovom distribucijom. Za dublje razumijevanje ovog koncepta možete se obratiti potpunijim knjigama o statistici.
Primjer izračuna intervala pouzdanosti za težine i visine dan je u [priloženim bilježnicama](notebook.ipynb).
| p | Srednja težina |
|-----|-----------|
| 0.85 | 201.73±0.94 |
| 0.90 | 201.73±1.08 |
| 0.95 | 201.73±1.28 |
Primijetite da što je veća vjerojatnost pouzdanosti, to je širi interval pouzdanosti.
## Testiranje hipoteza
U našem skupu podataka o igračima bejzbola postoje različite uloge igrača, koje se mogu sažeti u tablici ispod (pogledajte [priloženu bilježnicu](notebook.ipynb) kako biste vidjeli kako se ova tablica može izračunati):
| Uloga | Visina | Težina | Broj |
|------|--------|--------|-------|
| Catcher | 72.723684 | 204.328947 | 76 |
| Designated_Hitter | 74.222222 | 220.888889 | 18 |
| First_Baseman | 74.000000 | 213.109091 | 55 |
| Outfielder | 73.010309 | 199.113402 | 194 |
| Relief_Pitcher | 74.374603 | 203.517460 | 315 |
| Second_Baseman | 71.362069 | 184.344828 | 58 |
| Shortstop | 71.903846 | 182.923077 | 52 |
| Starting_Pitcher | 74.719457 | 205.163636 | 221 |
| Third_Baseman | 73.044444 | 200.955556 | 45 |
Možemo primijetiti da je prosječna visina igrača na prvoj bazi veća od one na drugoj bazi. Stoga bismo mogli zaključiti da su **igrači na prvoj bazi viši od igrača na drugoj bazi**.
> Ova izjava naziva se **hipoteza**, jer ne znamo je li činjenica zapravo istinita ili ne.
Međutim, nije uvijek očito možemo li donijeti ovaj zaključak. Iz prethodne rasprave znamo da svaka srednja vrijednost ima pridruženi interval pouzdanosti, pa ta razlika može biti samo statistička pogreška. Potrebno nam je formalniji način za testiranje naše hipoteze.
Izračunajmo intervale pouzdanosti zasebno za visine igrača na prvoj i drugoj bazi:
| Pouzdanost | Prva baza | Druga baza |
|------------|---------------|----------------|
| 0.85 | 73.62..74.38 | 71.04..71.69 |
| 0.90 | 73.56..74.44 | 70.99..71.73 |
| 0.95 | 73.47..74.53 | 70.92..71.81 |
Možemo vidjeti da se intervali ne preklapaju ni pod jednom razinom pouzdanosti. To dokazuje našu hipotezu da su igrači na prvoj bazi viši od igrača na drugoj bazi.
Formalnije, problem koji rješavamo je utvrditi jesu li **dvije distribucije vjerojatnosti iste**, ili barem imaju li iste parametre. Ovisno o distribuciji, za to trebamo koristiti različite testove. Ako znamo da su naše distribucije normalne, možemo primijeniti **[Studentov t-test](https://en.wikipedia.org/wiki/Student%27s_t-test)**.
U Studentovom t-testu izračunavamo tzv. **t-vrijednost**, koja pokazuje razliku između srednjih vrijednosti, uzimajući u obzir varijancu. Pokazano je da t-vrijednost slijedi **Studentovu distribuciju**, što nam omogućuje dobivanje granične vrijednosti za zadanu razinu pouzdanosti **p** (to se može izračunati ili pronaći u numeričkim tablicama). Zatim uspoređujemo t-vrijednost s ovom granicom kako bismo prihvatili ili odbacili hipotezu.
U Pythonu možemo koristiti paket **SciPy**, koji uključuje funkciju `ttest_ind` (uz mnoge druge korisne statističke funkcije!). Ona za nas izračunava t-vrijednost i također obavlja obrnuto traženje p-vrijednosti pouzdanosti, tako da možemo samo pogledati pouzdanost kako bismo donijeli zaključak.
Na primjer, naša usporedba visina igrača na prvoj i drugoj bazi daje nam sljedeće rezultate:
```python
from scipy.stats import ttest_ind
tval, pval = ttest_ind(df.loc[df['Role']=='First_Baseman',['Height']], df.loc[df['Role']=='Designated_Hitter',['Height']],equal_var=False)
print(f"T-value = {tval[0]:.2f}\nP-value: {pval[0]}")
```
```
T-value = 7.65
P-value: 9.137321189738925e-12
```
U našem slučaju, p-vrijednost je vrlo niska, što znači da postoje snažni dokazi koji podupiru tvrdnju da su igrači na prvoj bazi viši.
Postoje i druge vrste hipoteza koje bismo mogli testirati, na primjer:
* Dokazati da određeni uzorak slijedi neku distribuciju. U našem slučaju pretpostavili smo da su visine normalno distribuirane, ali to treba formalno statistički provjeriti.
* Dokazati da srednja vrijednost uzorka odgovara nekoj unaprijed definiranoj vrijednosti
* Usporediti srednje vrijednosti više uzoraka (npr. koja je razlika u razinama sreće među različitim dobnim skupinama)
## Zakon velikih brojeva i centralni granični teorem
Jedan od razloga zašto je normalna distribucija toliko važna je tzv. **centralni granični teorem**. Pretpostavimo da imamo veliki uzorak neovisnih N vrijednosti X1, ..., XN, uzorkovanih iz bilo koje distribucije sa srednjom vrijednošću μ i varijancom σ2. Tada, za dovoljno velik N (drugim riječima, kada N→∞), srednja vrijednost ΣiXi bit će normalno distribuirana, sa srednjom vrijednošću μ i varijancom σ2/N.
> Drugi način interpretacije centralnog graničnog teorema je reći da, bez obzira na distribuciju, kada izračunate srednju vrijednost zbroja bilo kojih slučajnih varijabli, završavate s normalnom distribucijom.
Iz centralnog graničnog teorema također slijedi da, kada N→∞, vjerojatnost da srednja vrijednost uzorka bude jednaka μ postaje 1. Ovo je poznato kao **zakon velikih brojeva**.
## Kovarijanca i korelacija
Jedna od stvari koje Data Science radi je pronalaženje odnosa između podataka. Kažemo da se dvije sekvence **koreliraju** kada pokazuju slično ponašanje u isto vrijeme, tj. ili rastu/padaju istovremeno, ili jedna sekvenca raste dok druga pada i obrnuto. Drugim riječima, čini se da postoji neka veza između dvije sekvence.
> Korelacija ne mora nužno ukazivati na uzročnu vezu između dvije sekvence; ponekad obje varijable mogu ovisiti o nekom vanjskom uzroku, ili može biti čista slučajnost da se dvije sekvence koreliraju. Međutim, jaka matematička korelacija dobar je pokazatelj da su dvije varijable na neki način povezane.
Matematički, glavni koncept koji pokazuje odnos između dvije slučajne varijable je **kovarijanca**, koja se izračunava ovako: Cov(X,Y) = **E**\[(X-**E**(X))(Y-**E**(Y))\]. Izračunavamo odstupanje obje varijable od njihovih srednjih vrijednosti, a zatim produkt tih odstupanja. Ako obje varijable odstupaju zajedno, produkt će uvijek biti pozitivna vrijednost, što će rezultirati pozitivnom kovarijansom. Ako obje varijable odstupaju nesinkronizirano (tj. jedna pada ispod prosjeka dok druga raste iznad prosjeka), uvijek ćemo dobiti negativne brojeve, što će rezultirati negativnom kovarijansom. Ako odstupanja nisu ovisna, zbrojit će se na približno nulu.
Apsolutna vrijednost kovarijance ne govori nam mnogo o tome koliko je jaka korelacija, jer ovisi o veličini stvarnih vrijednosti. Da bismo je normalizirali, možemo podijeliti kovarijancu sa standardnom devijacijom obje varijable kako bismo dobili **korelaciju**. Dobra stvar je što je korelacija uvijek u rasponu [-1,1], gdje 1 označava jaku pozitivnu korelaciju između vrijednosti, -1 jaku negativnu korelaciju, a 0 nikakvu korelaciju (varijable su neovisne).
**Primjer**: Možemo izračunati korelaciju između težina i visina igrača bejzbola iz gore spomenutog skupa podataka:
```python
print(np.corrcoef(weights,heights))
```
Kao rezultat, dobivamo **matricu korelacije** poput ove:
```
array([[1. , 0.52959196],
[0.52959196, 1. ]])
```
> Matrica korelacije C može se izračunati za bilo koji broj ulaznih sekvenci S1, ..., Sn. Vrijednost Cij je korelacija između Si i Sj, a dijagonalni elementi su uvijek 1 (što je također samokorelacija Si).
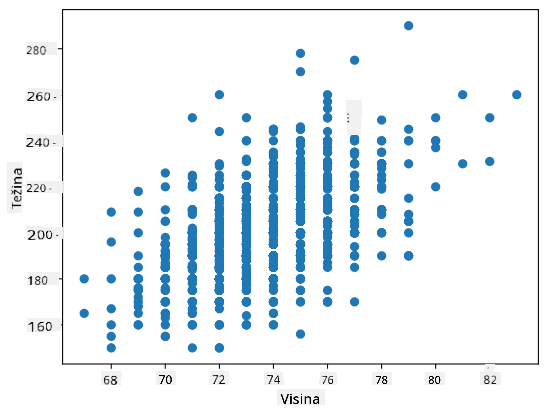
U našem slučaju, vrijednost 0.53 ukazuje na to da postoji određena korelacija između težine i visine osobe. Također možemo napraviti scatter plot jedne vrijednosti u odnosu na drugu kako bismo vizualno vidjeli odnos:

> Više primjera korelacije i kovarijance možete pronaći u [priloženoj bilježnici](notebook.ipynb).
## Zaključak
U ovom odjeljku naučili smo:
* osnovna statistička svojstva podataka, poput srednje vrijednosti, varijance, moda i kvartila
* različite distribucije slučajnih varijabli, uključujući normalnu distribuciju
* kako pronaći korelaciju između različitih svojstava
* kako koristiti matematički i statistički aparat za dokazivanje hipoteza
* kako izračunati intervale pouzdanosti za slučajnu varijablu na temelju uzorka podataka
Iako ovo definitivno nije iscrpan popis tema unutar vjerojatnosti i statistike, trebao bi biti dovoljan za dobar početak ovog tečaja.
## 🚀 Izazov
Koristite uzorak koda u bilježnici za testiranje drugih hipoteza:
1. Igrači na prvoj bazi su stariji od igrača na drugoj bazi
2. Igrači na prvoj bazi su viši od igrača na trećoj bazi
3. Shortstopovi su viši od igrača na drugoj bazi
## [Kviz nakon predavanja](https://purple-hill-04aebfb03.1.azurestaticapps.net/quiz/7)
## Pregled i samostalno učenje
Vjerojatnost i statistika su toliko široka tema da zaslužuju vlastiti tečaj. Ako želite dublje ući u teoriju, možda biste željeli nastaviti čitati neke od sljedećih knjiga:
1. [Carlos Fernandez-Granda](https://cims.nyu.edu/~cfgranda/) s New York University ima odlične bilješke s predavanja [Probability and Statistics for Data Science](https://cims.nyu.edu/~cfgranda/pages/stuff/probability_stats_for_DS.pdf) (dostupno online)
1. [Peter i Andrew Bruce. Practical Statistics for Data Scientists.](https://www.oreilly.com/library/view/practical-statistics-for/9781491952955/) [[uzorak koda u R](https://github.com/andrewgbruce/statistics-for-data-scientists)].
1. [James D. Miller. Statistics for Data Science](https://www.packtpub.com/product/statistics-for-data-science/9781788290678) [[uzorak koda u R](https://github.com/PacktPublishing/Statistics-for-Data-Science)]
## Zadatak
[Mala studija o dijabetesu](assignment.md)
## Zasluge
Ovu lekciju napisao je s ♥️ [Dmitry Soshnikov](http://soshnikov.com)
---
**Odricanje od odgovornosti**:
Ovaj dokument je preveden pomoću AI usluge za prevođenje [Co-op Translator](https://github.com/Azure/co-op-translator). Iako nastojimo osigurati točnost, imajte na umu da automatski prijevodi mogu sadržavati pogreške ili netočnosti. Izvorni dokument na izvornom jeziku treba smatrati autoritativnim izvorom. Za kritične informacije preporučuje se profesionalni prijevod od strane čovjeka. Ne preuzimamo odgovornost za bilo kakva nesporazuma ili pogrešna tumačenja koja proizlaze iz korištenja ovog prijevoda.